Perfect photon absorption based on the optical parametric process∗

Yang Zhang(张旸) Yu-Bo Ma(马宇波) Xin-Ping Li(李新平) Yu Guo(郭钰) and Chang-Shui Yu(于长水)

1Institute of Theoretical Physics,Shanxi Datong University,Datong 037009,China

2Institute of Quantum Information Science,Shanxi Datong University,Datong 037009,China

3School of Physics,Dalian University of Technology,Dalian 116024,China

Keywords: photon absorption,cavity quantum electrodynamics,optical parameter amplifier

1. Introduction

With the rapid development of quantum information and quantum communication, photons as the carrier of the information can be utilized for the transmission of information over extended distances. Consequently, the study of photon behaviors plays a fundamental role in quantum physics and how to control photons has become a conspicuous focus in quantum physics.[1–4]In general, the communicating information needs some form of interaction between the signals. In the case of lights, this can be implemented by controlling light by light,[5,6]which yields many novel coherent phenomena,such as electromagnetically induced transparency(EIT),[6–8]electromagnetically induced absorption,[9,10]optomechanically induced transparency(OMIT),[11–15]optomechanically induced absorption (OMIA),[16,17]and so on. Recently,an analog of above phenomenon(coherent perfect photon absorption) has aroused widespread interest and attracts a great deal of attention in recent studies. It has been enabled to control light in an efficient and coherent way.[18–33]Normally,the coherent perfect photon absorption is occurring when two or more coherent lights overlap, leading to a spatial redistribution of energy. In other words,it is based on the destructive interference between the input lights.[34–38]Abundant phenomena and potential applications of perfect photon absorption have been predicted or demonstrated, including optical switch,[19,22,33,39–41]radar cloaking,[42]molecular detection.[43,44]Moreover, the perfect photon absorption has also been investigated in various systems, including, but not limited to, the whispering-gallery-mode micro-resonators,[45]the coupled atom-resonator-waveguide system,[46]second harmonic generation,[47]nanostructured graphene film,[48]and strongly scattering media.[49]

A typical example of the physical platform is the cavity quantum electrodynamics (CQED) system, which is a fundamental model of light and matter that has been both theoretically and experimentally implemented.[50–52]In earlier studies, the perfect photon absorption has also been observed in the CQED system.[25,26,28,29]Nevertheless,none of these previous works considered the role of the relative phase, in further controlling the perfect photon absorption. The parameter conditions for the perfect photon absorption in these CQED systems are independent of the relative phase. However, the relative phase cannot be omitted when the two injected fields are un-identical in experiment as usual. In this context,a weak question is: whether one can find a potential quantum system to reveal how to use the relative phase to control the perfect photon absorption.

In recent years, the optical parametric amplifier (OPA)as a well-known nonlinear optical process has attracted great attention. Some of the interesting works have been proposed to improve the performance of the systems and exhibit a rich set of quantum phenomena, involving quantum information processing,[53]coupling amplification,[54,55]frequency conversions,[56]the generation of the unconventional blockade,[56,58,59]the manipulation of the photon transport,[60]mechanical squeezing,[61]ultrahigh-precision position detection,[62]enhancing the weak-force sensing,[63]and so on. It will be interesting if the photons can be coherently trapped and cannot be transmitted into either of the output channels due to the OPA interaction. In this paper,we propose a feasible scheme of coherent perfect photon absorption based on a hybrid CQED system,which consists of a degenerate OPA.In such a hybrid system,we report that the parametric phase can be controlled to realize the perfect photon absorption. Our results show that,in contrast to previous predictions of perfect photon absorption in atomic system,the emergence of OPA provides an important help for the realization of the perfect photon absorption, and it can be induced by the relative phase of the two injected fields in our system. The paper is arranged as follows. In Section 2, we study the case that only one field is injected into the cavity. We show that the perfect photon absorption can be observed in this case, and the destructive interference can be achieved via the OPA interact with cavity field. In Section 3, we discuss the case with two injected fields as well as with the OPA interaction,we find that the parametric phaseθcan induce the destructive interference,and it shows the similar photon absorption phenomenon with the one injected field case. The results also show that in absence of the parametric phaseθ,the perfect photon absorption can be induced by the relative phaseϕ.Finally,the discussions and conclusions are given in Section 4.

2. Perfect photon absorption in one side cavity

As schematically shown in Fig. 1, we consider a typical hybrid cavity QED system which consists of a bare optical cavity and a degenerate optical parameter amplifier(OPA)trapped in the cavity. In the rotating frame of the input laser frequency,the full Hamiltonian with regard to the driving and the dissipation,is given by(set=1 hereafter)

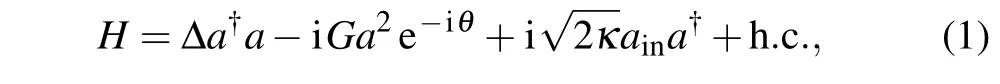
whereadenotes the cavity mode with the resonance frequencyωa,κis the loss rate of the cavity field on the cavity mirror.Hereainis the input field upon the cavity with the frequencyωl.∆=ωa−ωlis the laser detuning from the cavity mode,Gdenotes the nonlinear Gain of the OPA and produces some change in the cavity frequency,andθis the phase of the field driving the OPA.

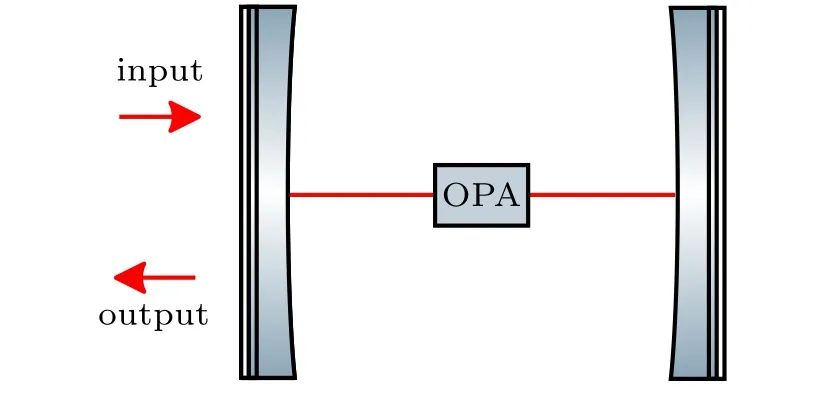
Fig.1. Schematic setup. The CQED system consists of a degenerate optical parameter amplifier in the cavity which is driven by one input light field.

Based on Hamiltonian Eq. (1) and the potential dissipation processes, one can derive the dynamics of the system from the Heisenberg equations of the operators. In the classical limit, one can replace the operators by their expectation values,thus the equations of motion for the expectation values of the operators can be expressed as follows:

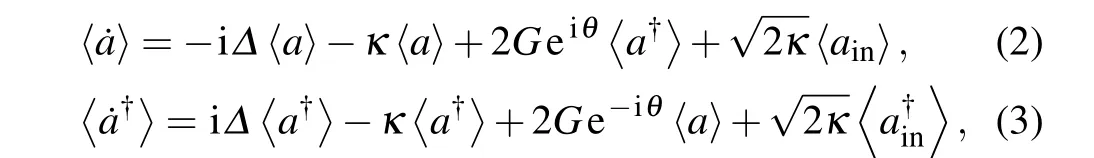
where〈···〉represents the expectation value over the steady state.Combining the above equations and calculate the steadystate solutions,one can obtain the dynamics of the system,the intra-cavity field can be obtained as

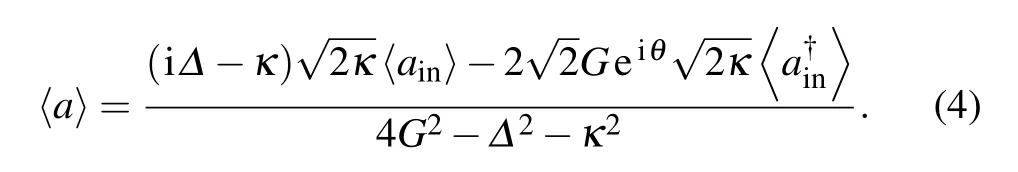
From Eq.(4),one can get the intra-cavity intensity|a|2.

Now let us turn to obtain the properties of the output field intensity, one should find the steady states of the output light field,we have to consider the input–output relation:[64]

Let us now focus our attention on how to use the OPA interaction to realize the perfect photon absorption. Generally,when a cavity photon field has the photon absorption effect,it implies that the output field intensity should be vanished,i.e.,|aout|2=0. When set|aout|2=0,we can get two specific conditions for the perfect photon absorption from Eq.(6):

In terms of the two conditions, one can find that the value of cavity detuning and the parametric phaseθshould satisfy with the certain parameter conditions. Intuitively,the photon detector cannot detect any photons. That is, the photon cannot go through out of the system. Then one can harness the system’s parameters to control the photon absorption. For example,we can control the parametersθand the parametric strengthGto match Eqs. (7) and (8), thus the output field intensity will vanish.

0～3岁是机体中枢神经系统发育最迅速、代偿能力最好的时期，也是脑细胞增殖，产生脑沟回、髓鞘形成的关键时期[8-9]。这时期大脑具有良好的重组功能，若此时给予良性刺激，可促进大脑结构及功能的代偿，其中包括轴突绕道投射、树突异常分叉，产生超常规的神经突触等，但随着大脑的发育成熟，其重组功能就不会出现了[10]。

In Fig.2,we numerically evaluate the output field intensity,the figure shows the output field intensity|aout|2/|ain|2as a function ofθwith the different values ofG.From Fig.2,one can find that there exists two perfect photon absorption points in one period of the parametric phaseθ. When the parametric phaseθtakes the particular values,i.e.,θ=±arccos(κ/2G),the injected field’s transmitted part interferes destructively with the reflected part. It means that although the single input field is injected into the cavity,the destructive interference can still be occurred. This interesting phenomenon tells us that one can use the degenerate OPA interaction to achieve the perfect photon absorption in the case of one driving field. In this case, due to the existence of the OPA, the photons generated by the photon–photon parametric process can interfere with the photons directly of the injected field. Moreover,from the curves, one can find that with the different values of the parametric gainG,the perfect photon absorption occurs at two special points all the time,and it does not matter ifGis greater thanκor not. In addition,one can also find the different values of parametric strengthGhave a significant effect on the locations of the perfect photon absorption channels,it changes the width between the two absorption dips, and the width is governed nearly linearly by the parametric strength.

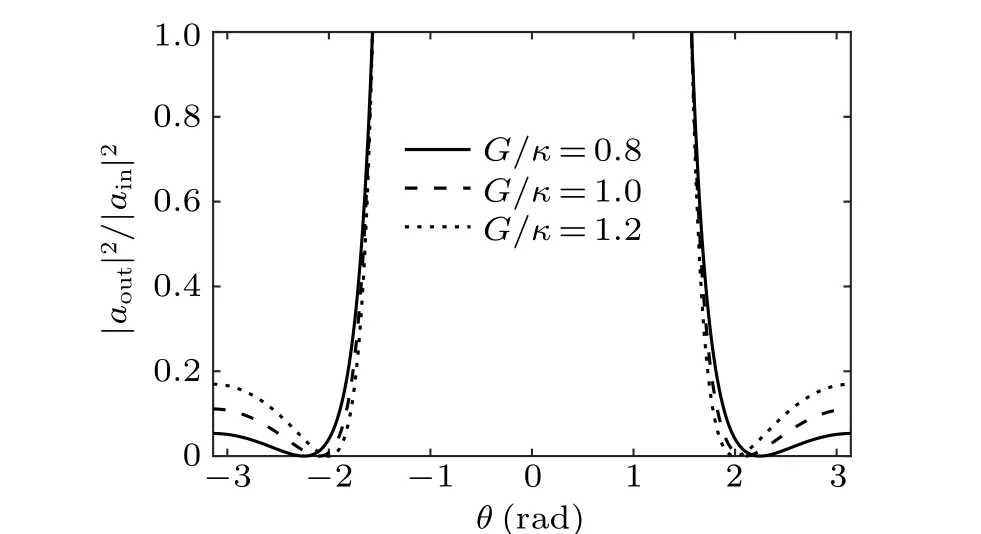
Fig. 2. The output light intensity|aout|2/|ain|2 as a function of the driving phase θ with the different nonlinear gain parameter G/κ. The solid line corresponds to G/κ =0.8, the dotted curve corresponds to G/κ =1, and the dashed line corresponds to G/κ =1.2.

3. Perfect photon absorption in two side cavity

In the above section, we have found that the parametric phase can be used to generate the perfect photon absorption when only one laser field is injected into the system. To better understand the phase effects on the perfect photon absorption,we will focus on the general case,i.e.,two lasers are injected into the two sides of the cavity,which is shown in Fig.3. As it is described in Refs.[25–27,65,66],considering the two fields being injected into cavity and in the rotating frame of the input laser frequency,we have(set=1 hereafter)

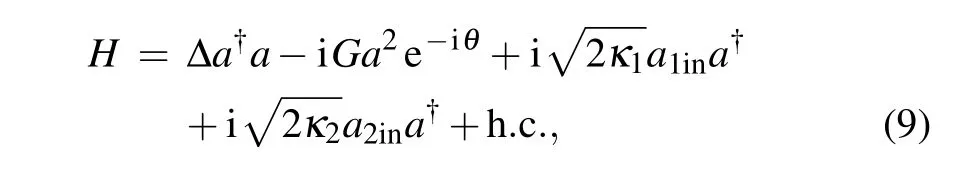
wherea1inanda2inare two input fields upon the cavity with the same frequencyωl,κi(i=1,2)is the loss rate of the cavity field on the cavity mirror.

Using the same method as above section,one can get the Heisenberg equations of the operators. The equations of the expectation values for the cavity field operator can be written as

From the input–output relation, the output fields can be given as[64]

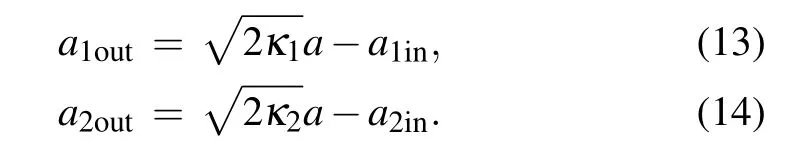
One can assume thata1in=|ain|,a2in= eiϕ|ain|,whereϕdenotes the relative phase of the two opposite input fields. We also consider a symmetric cavity withκ1=κ2=κ/2. Furthermore,the output intensities are written as follows:

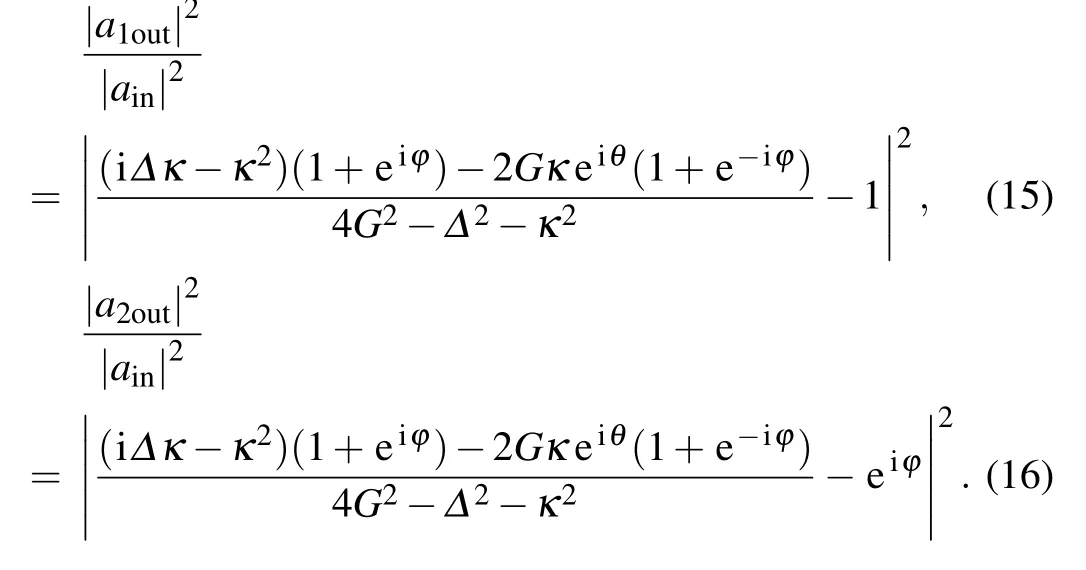
From Eqs.(15)and(16),one can obtain the properties of the two injected fields. In particular,on can also observe that the perfect photon absorption of the two input fields depends on the parametric phaseθand the relative phaseϕ. The perfect photon absorption impliesa1out=a2out=0. Without loss of generality,we first investigate how the parametric phase influence the perfect photon absorption phenomenon in the presence of the two injected fields. We would like to note that the previous studies[25,26,28,65,66]stated the perfect photon absorption in the atomic CQED system will not happen at any rate once the relative phase satisfied with the condition:ϕ/=2kπ,k=0,±1,±2,....For the sake of the generality,we will begin our analysis by considering the caseϕ=0,thus we can get the corresponding parameter conditions for the perfect absorption as

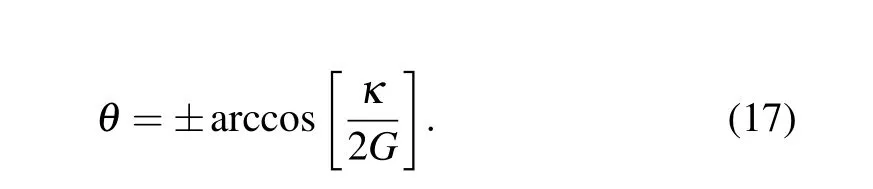
When we setϕ=0,the output field intensities are equal to each other for the two injected lasers. In terms of Eqs.(17),one can discuss some pertinent results about the perfect absorption induced byθ. Compared to the case of one side cavity, the new perfect absorption conditions for the two side cavity nearly are nearly unchanged. Thus in the two injected fields case,the proposed mechanism withϕ=0 does not have a major impact on the perfect photon absorption. The destructive interference of two injected fields caused by the parameter phase has not produce any new optical phenomenon and has not any additional effect on the realization of perfect photon absorption. This can be explained as follows, in the absence of the relative phase, the perfect photon absorption is mainly dependent on the perfect destructive interference between the left-going and right-going field,which is caused by the parameter phase. It means that the hybrid system can be regarded as an ideal optical absorber with one or two injected fields under the same parameter conditions.

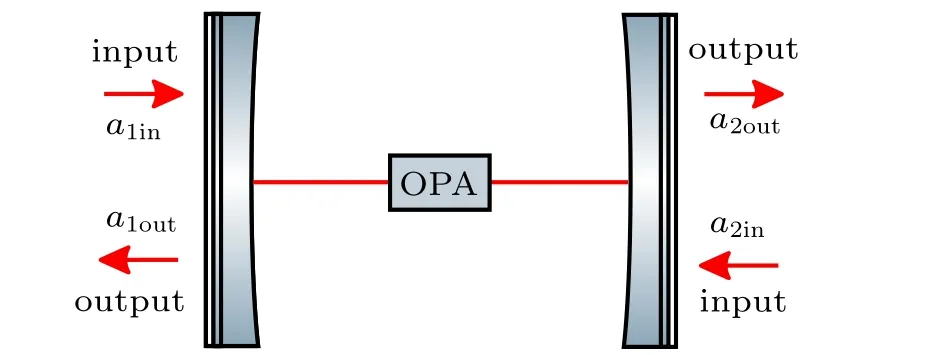
Fig. 3. Schematic diagram of the CQED system. An optical cavity mode couples an optical parametric amplification and with two injected fields.

Now let us consider the question: whether the perfect photon absorption can be achieved if theϕ/=0. We expect that the perfect photon absorption can be caused by the relative phase, which can be used to enhance the perfect photon absorption,or has a positive effect on the optical interference in the hybrid system. In other words, we will focus our attention on how to use the relative phaseϕto realize the perfect photon absorption. For simplify, we will setθ=0,then one can obtain the perfect photon absorption conditions. Due to the relative phaseϕ,the perfect photon absorption conditions are different for the two output fielda1outanda2out. Fora1out=0,the perfect photon absorption conditions can be expressed as:

Similarly,in the case ofa2out=0,the perfect photon absorption can be obtained by the following two algebraic equations

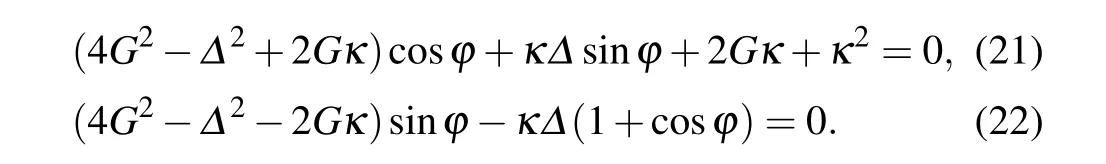
By a simple calculation,equations(21)and(22)can lead to a cubic equation about the relative phaseϕ,which corresponds to the perfect photon absorption points. We can extract the required perfect photon absorption condition and find where the perfect photon absorption occurs. Thus the specific values ofϕare given as follows:

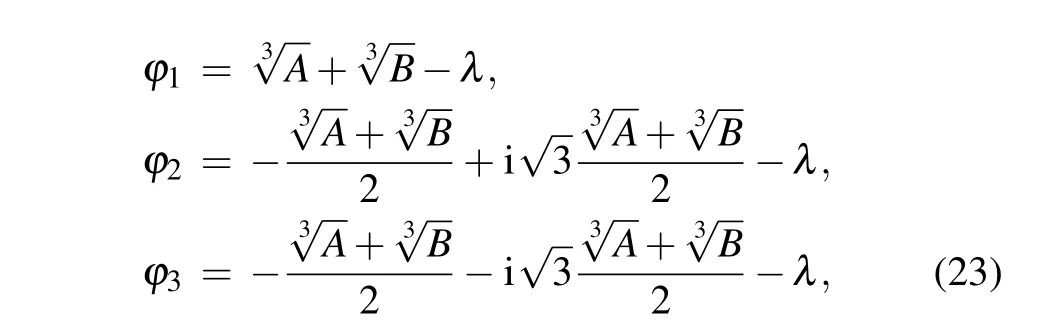
where

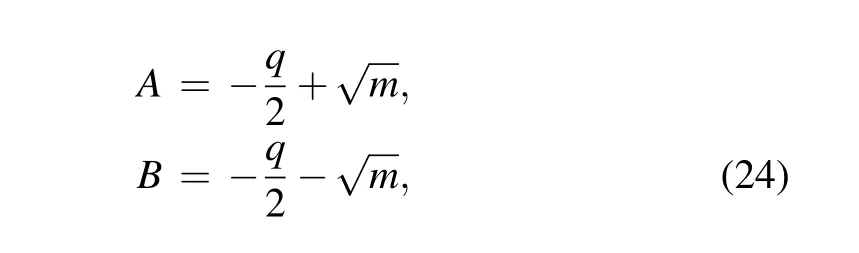
with

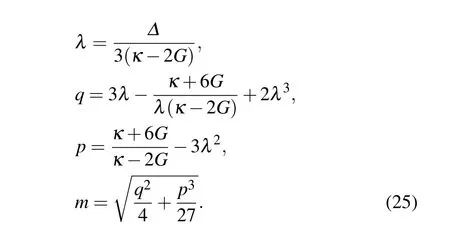
Based on Eq. (23), one can analytically estimate in this regime that the intensity of the output fields is determined by the values ofϕ,and that equalling this to the relative phase induced the perfect photon absorption. In what follows,we will present the result for the two normalized output light intensities|a1out|2/|ain|2and|a2out|2/|ain|2for the hybrid system in Figs.4 and 5 with|a1in|=|ain|,|a2in|= eiϕ|ain|,which shows that the relative phase has an important effect on the photon absorption.

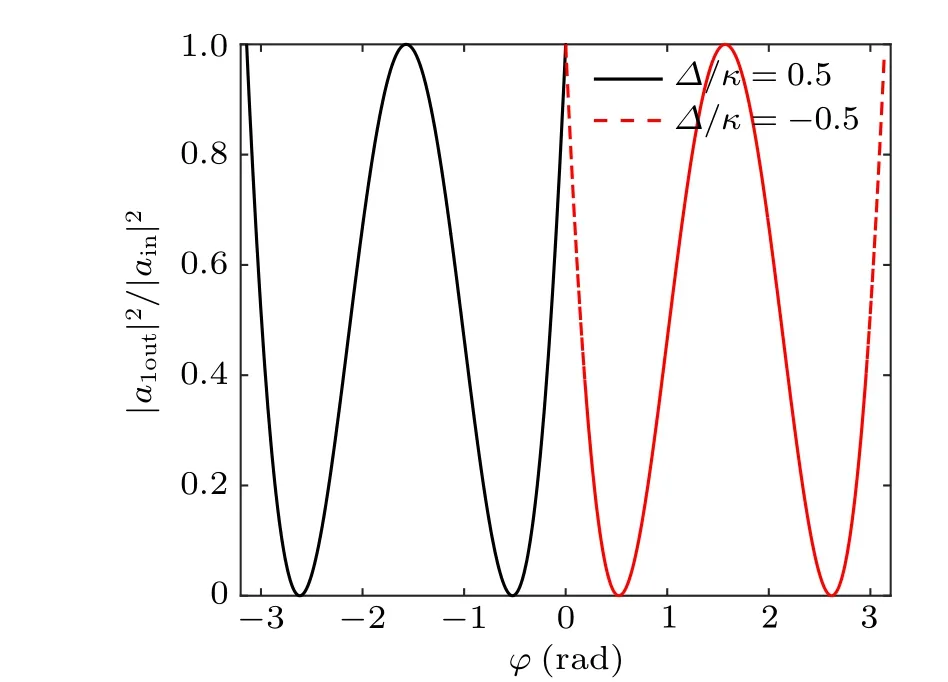
Fig.4. The output intensity|a1out|2/|ain|2as a function of the relative phase ϕ. Here,the black solid line corresponds to ∆/κ =0.5 and the red dashed line corresponds to ∆/κ=-0.5.

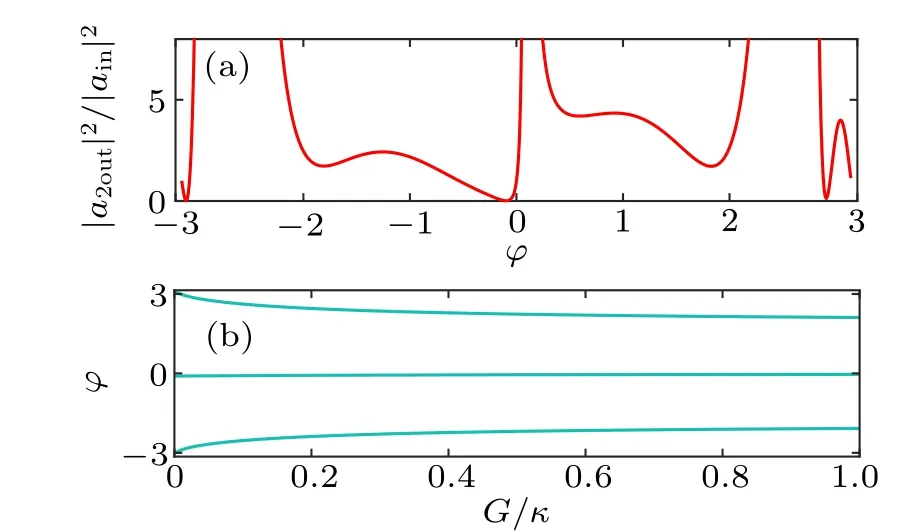
Fig. 5. (a) The output intensity |a2out|2/|ain|2 as a function of the relative phase ϕ with G=(κ tan3 ϕ/2+κ tanϕ/2+∆tan2 ϕ/2+∆)/(2tan3 ϕ/2+6tanϕ/2) and ∆/κ =0.1. (b) The relative phase ϕ versus the parametric gain G with ∆/κ =0.1.

At last, we want to mention that, the perfect photon absorption always occurs under the strong coupling regime in the CQED system coupled with the atomic ensemble.[25,26,28]To further investigate whether the strong coupling strength is required or not, we numerically calculate the matched relation between the relative phaseϕand the coupling strength parameterG,which is shown in Fig.5(b). By solving Eqs.(21)and(22), one can find that the system’s parameters are satisfied with the mathematical expression

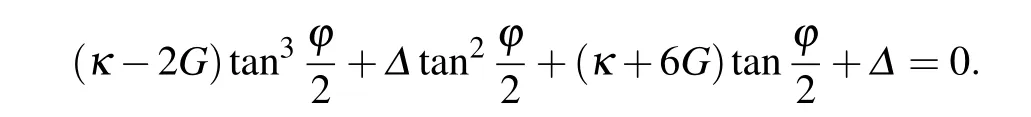
From Fig. 5(b), it is clear that when 0＜G/κ ＜1, the relative phaseϕhas three available values to achieve the perfect absorption all the while in one period. Thus one can say that the current system coupled with the OPA can have three perfect photon absorption points which are caused by the relative phase even though in the weak coupling regime. It means that the relative phaseϕcan induce the interference between the transmitted field and the reflected field, and achieve three channels destructive at the right output port in the hybrid cavity system.

4. Conclusions and discussion

In summary,we have considered a hybrid CQED system consisting of an OPA. The main contribution of this work is that we propose a potential scheme to observe the perfect photon absorption via the parametric phase and the relative phase.We would like to point that, the parametric processes inside the cavity can change the interference channels of the injected fields, and the photon behaviors of the output fields become newfangled. We find that when only one laser field injected into the field, the perfect photon absorption can also be generated, which is in contrast to the previous studies,[25,27,65,66]

where the perfect absorption is based on the destructive interference between the two input fields.

Moreover, in the absence of the parametric phase, one can also observe the perfect photon absorption,with the nonvanished relative phase with the two injected fields. The result show that the perfect photon absorption can be controlled by adjusting the relative phase,and an additional perfect photon absorption point compared to the parametric phase can be induced. In other words, the existence of the perfect photon absorption depends on the optical interference induced by the relative phase. In addition, we also want to mentioned that,unlike the conventional perfect photon absorption,[25,26,65,66]the perfect photon absorption can also be achieved via tuning the parametric phase or relative phase and is independent of the strong coupling regime. That is to say,in experiment,the considered system can be built under a more reasonable condition. Our results manifest that, the use of parametric processes could provide us with a way to controlling the behaviors of photons and takes advantage of the parametric phase and relative phase to achieve the perfect photon absorption.In a broader view, the considered scheme could be useful for abundant application in quantum optical devices by control the phases.

In the review process of the paper, we noticed a very recent publication[27]in which an optimal coherent perfect photon absorption scheme induced by atom and second-order nonlinear crystal is proposed. Their work is more concerned with perfect photon absorption and bistable branches synergies in the weak-coupling regime. Different from the mechanism this work reported,we mainly want to investigate the interference effects caused by the parametric phase and the relative phase,and our purpose is to find the way to use the parametric phase and the relative phase to control the perfect photon absorption.