Behaviors of thermalization for the Fermi–Pasta–Ulam–Tsingou system with small number of particles∗

Zhenjun Zhang(张振俊), Jing Kang(康静), and Wen Wen(文文)

College of Science,Hohai University,Nanjing 210098,China

Keywords: FPUT system,thermalization,small number of particles

1. Introduction

To confirm the connection between nonlinearity and ergodicity in a classical Hamiltonian system with many degrees of freedom, Fermi in collaboration with Pasta, Ulam, and Tsingou(FPUT)performed the first numerical experiment via a one-dimensional harmonic chain coupled with cubic or quartic potentials.[1]They expected that the nonlinearity would lead to a thermalized state,i.e., a state in which the influence of the initial modes disappears and all modes are excited equally on average. Instead of the expected irreversible process of thermalization,the system exhibits a quasiperiodic recurrences to the initial state. Their work has stimulated prolific activities for several decades in the study of the temporal evolution of an initially localized energy excitation in various nonlinear systems.[2–38]

Izraielev and Chirikov predicted there is an energy threshold, above which the FPUT system can reach thermalization.[3]Such concept, also known as the Chirikov overlap criterion, is based on the fact that the nonlinearity changes the linear dispersion relation, and the resonant condition in frequency is then modified. When the nonlinearity becomes large enough, a mechanism of “overlap of frequencies”may happen. Fast thermalization has been subsequently confirmed by different numerical studies.[4,8,9,14,15]However,whether the FPUT system can be thermalized for arbitrary small nonlinearity has not been settled clearly. Recently,resonant wave–wave interaction theory has been applied to discuss this problem.[39–47]According to this theory,the long time dynamics is ruled by exact resonances in weak nonlinear regime.Thermalization is achieved by the nontrivial resonances.In the thermodynamic limit,if the nontrivialn-wave resonances exist and dominate the thermalization,the thermalization time-scale should be the derivation of the correspondingn-wave kinetic equation, which lead to the thermalization timeteqdepending on system’s energy densityεscales asteq∝ε−(n−2).[41,45]For the FPUT system in the thermodynamic limit, the lowest order nontrivial resonances are four-wave resonances, which result inteq∝ε−2. Numerical simulations for large number of particles show that the results are mostly consistent with theoretical predictions.[45,46]Besides, the thermalization behaviors for one-dimensional disordered lattices systems in the thermodynamic limit have been studied recently.[48,49]For the FPUT system with small number of particles using periodic boundary conditions, the lowest order nontrivial resonances were found to be six-wave resonances.[42,43,46]However, then-wave kinetic equation can be rigorously derived only in the thermodynamic limit. For the FPUT system with small number of particles,deriving a discrete version of the kinetic equation poses significant mathematical problems.[46]Therefore,they made the conjecture that the time scale of thermalization corresponding to the six-wave interaction for small number of particles is equivalent to that for the thermodynamic limit,which leads toteq∝ε−4. This scaling law has been verified by their numerical simulations in the range of nonlinearity they studied.[42,43,46]Obviously, the discrete case stands on a less rigorous ground and further work is definitely needed.

In this paper, we study the behaviors of thermalization for the FPUT system in a wider range of weak nonlinearity compared with previous studies.[42,43]We find the scalingteq∝ε−4observed in Refs. [42,43] is only established within a certain range of nonlinearity. In this range of nonlinearity, energies can transfer from the initial excited modes to other modes continuously. This energy transport process happens via the nontrivial six-wave resonances,[42,43]which hence lead toteq∝ε−4. With a further decreasing nonlinearity, a crossover fromteq∝ε−4to a steeper growth will appear. In the very weakly nonlinear regime, energy transport process becomes obviously different. Energies on low frequency modes are found to be frozen on large time scales. It indicates that these low frequency modes cannot take part in the energy sharing for a long time. Therefore,resonant wave–wave interaction theory no longer works for energy transport in the very weakly nonlinear regime. In this case, redistribution of mode energies happens through the resonances of high frequency modes,which lead to the deviation fromteq∝ε−4.

2. Model and method of numerical experiments

Hereqjis the displacement of the particlejfrom its equilibrium position andpjis the associated momentum.Nis the particle number of the system.αandβare positive constants.α/=0,β=0 andα=0,β/=0 correspond to theα-FPUT model andβ-FPUT model, respectively. The relevant quantities determining the dynamics areα2ε[30]andβε[31]forα-FPUT model andβ-FPUT model, respectively. A more systematic definition of nonlinearity strength for one-dimensional lattices can be found in Ref. [50]. In the linear case (α=0,β=0)with periodic boundaries(qN=q0),the normal modes are given by

wherePkandQkare the momentum and amplitude of thek-th normal mode,respectively.

The dispersion relation(frequencyversusmode indexk)i

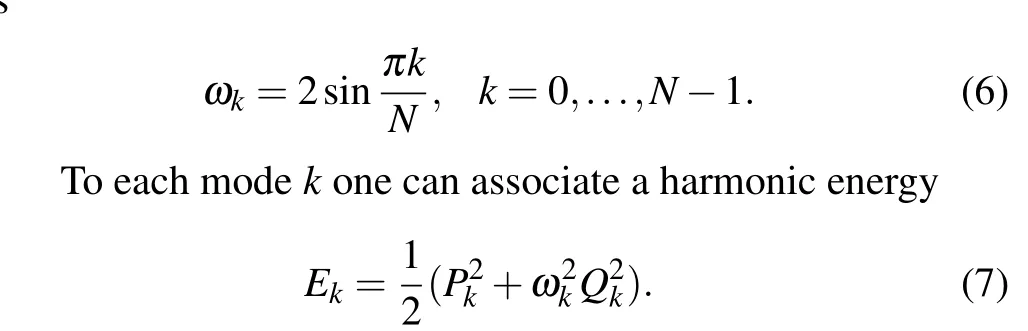
We introduce the following quantity as an indicator of thermalization[8]

where

in which

We use an SABA2C symplectic algorithm[51]to integrate the equations of motion derived by the Hamiltonian (1). Energy is initially equidistributed among some of the lowest frequency linear modes. The time step was set to 0.1 in all simulations, and it was checked that from beginning to the end of the simulation the relative energy error keeps smaller than 10−5. Note that the relevant quantities determining the strength of nonlinearity areα2ε[30]andβε[31]forα-FPUT model andβ-FPUT model,respectively.Therefore,it is equivalent to study the scaling ofα(β)by fixingεor that ofεby fixingα(β). Here,without loss of generality,we vary the energy densityεand fixα=0.33[30]andβ=1.0 forα-FPUT model andβ-FPUT model, respectively. Particle number of the system isN=32. In order to suppress fluctuations, the result ofξ(t) is averaged on 50 different random phases for eachε. We use〈ξ(t)〉to denote the averaging results.

3. Numerical results

In Fig. 1(a), we show the results of〈ξ(t)〉for different energy densityεforα-FPUT model in semilog scale. Modesk=1,2,30,31 are initially excited for allε. The curves start at the value 4/(N −1) then settle to intermediate values for a transient interval of time that increases as the energy densityεdecreases. After that, the curves grow gradually and finally tend to 1.0 with the time increasing. In order to obtain the scaling law of thermalization timeteqdepending onε,we introduce a threshold〈ξ〉eqto estimate the time it takes for the system to reach thermalization. Specifically, we have defined the time asteqin which〈ξ(t)〉reaches the value of〈ξ〉eq=0.99. We find the scaling law ofteqdepending onεis quite insensitive to the choice of the value of〈ξ〉eq. This can be seen from the rescaled results of〈ξ(t)〉for differentεshown in Fig. 1(b). We rescale〈ξ(t)〉for differentεas the time is divided by a suitable factor so that they superpose at〈ξ(t)〉=0.9. One can see that all curves nearly collapse to a single one when〈ξ(t)〉is greater than 0.7.

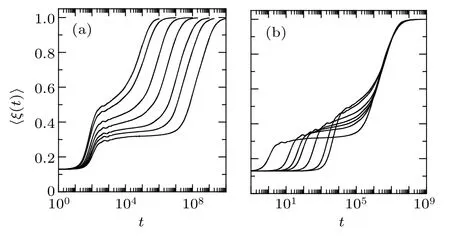
Fig. 1. (a) The dependence of 〈ξ(t)〉 on time t for different energy density ε for α-FPUT model in semilog scale. The curves from left to right at 〈ξ(t)〉=0.8 are for ε =0.1, 0.08, 0.05, 0.035, 0.025, 0.02, and 0.015,respectively. Modes k=1,2,30,31 are initially excited for each ε. (b)The curve of ε=0.035 is kept fixed. The other curves are rescaled as the time is divided by a suitable factor so that they superpose at〈ξ(t)〉=0.9.

Fig.2.The results of thermalization time teq depending on ε in log–log scale for α-FPUT model.

The results ofteqdepending onεforα-FPUT model are shown in Fig.2.One can see that a power law scalingteq∝ε−4is observed within a certain range ofε. This scaling has been found in Ref.[42]. However, a deviation fromteq∝ε−4will appear with a further decreasingε.This deviation has not been observed in Ref.[42]because the strength of nonlinearity they studied is not small enough. One can see from Fig.2 that an obvious deviation fromteq∝ε−4appears atεc≈0.025.Therefore,α2εc≈(0.33)2×0.025≈0.0027. A deviation fromteq∝ε−4can be observed only when the value ofα2εis less than 0.0027. However, one can see from Ref. [42] that the smallest value ofα2ε ≈(0.06)2×1.0=0.0036,above which only the scalingteq∝ε−4can be observed.The deviation fromteq∝ε−4is found to be independent of the number of the initially excited modes.

The results ofteqdepending onεforβ-FPUT model in log–log scale are shown in Fig.3.The scalingteq∝ε−4,which has been found in Ref.[43], is observed only when the value ofεis grater thanεc≈0.014. With a further decreasingε, a deviation fromteq∝ε−4appears.Therefore,this deviation can be observed only when the value ofβεis less than 0.014. In Ref.[43],the smallest value ofβε ≈0.02,above which only the scalingteq∝ε−4can be observed.

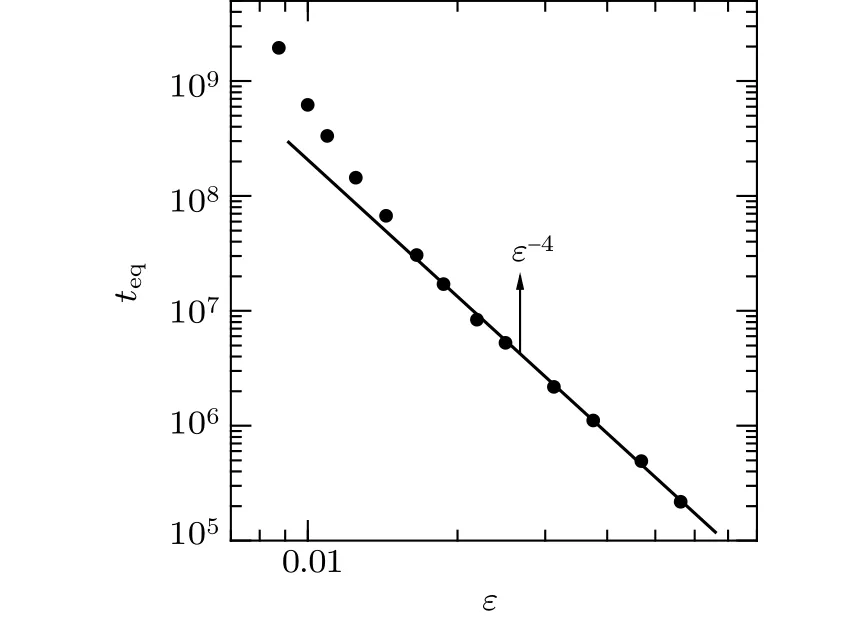
Fig.3.The results of thermalization time teq depending on ε in log–log scale for β-FPUT model.

According to the resonant wave–wave interaction theory,[41]all modes of the FPUT system with small number of particles for periodic boundary conditions are interconnected via the nontrivial six-wave resonances.[42,43]Therefore, energies can exchange among all modes continuously through the nontrivial wave–wave interaction until reaching the thermalized state. In other words,energy on each mode should varies continuously with time until reaching the thermalized state if energy can spread via the nontrivial wave–wave interaction.Figure 4(a)gives the results ofEk(t)depending ontwith differentkforα-FPUT model atε=0.05. It is seen that the energy on each mode varies continuously with time,and fnially approaches to the expected value 0.05,which means thermalization has reached. Figure 4(b) gives the results ofEk(t)versus kforε=0.05 at different timetforα-FPUT model.One can see that each mode at different time owns different energy. The above results indicate that energies can interchange among all modes continuously. This energy transfer behavior is consistent with the resonant wave–wave interaction theory. Therefore,resonant wave–wave interaction theory works well in this range of nonlinearity. The lowest order nontrivial resonances have been found to be six-wave resonances,[42,43]which hence lead to the power law scalingteq∝ε−4. However,energy transport process becomes obviously different in

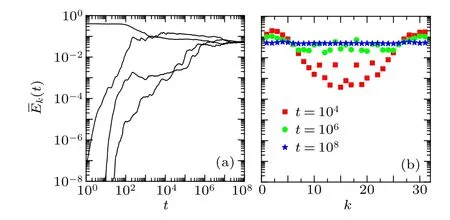
Fig.4. (a)TheresultsofEk(t)dependingont withdifferent k for α-FPUT model at ε=0.05. Thecurves fromtop tobottomatt =104 are fork=1,5,10,and 16,respectively. Modes k=1,2,30,31 are initially excited. (b)Parameters are the same as those in panel(a),but now for the results of Ek(t)versus k at different time t.

Fig.5. (a)The resultsofEk(t)depending on twithdifferent k for α-FPUT model atε=0.01.The curvesfromtop to bottom att=104 are for k=1,5,10,and 16,respectively. Modes k=1,2,30,31 have been initially excited.(b)Parameters are the same as those in panel(a),but now for the results of Ek(t)versus k at different time t.

In order to obtain the scaling law in the very weakly nonlinear regime,we study the normalized high frequency energyσ(t)=∑21k=11Fk(t), as has been studied in Ref. [30] for theα-FPUT system with fixed boundary conditions. For theα-FPUT system with fixed boundary conditions, the results ofσ(t) for differentεare found to be fitted by a power lawσ(t)∝Dtγ.[30]Both the exponentγand the coefficientDdepend onε.According to this power law,the values ofteqcan be obtained only via relatively short time scales even in the very weakly nonlinear regime. The thermalization timeteqdepending onεis found to beteq∝10c/εb, with suitable constantscandb, in the very weakly nonlinear regime.[30]However,the dynamical results ofσ(t)for the FPUT system with periodic boundary conditions are different from those with fixed boundary conditions. In Fig. 6, we plot the results ofσ(t)versus tfor two values ofε=0.008, 0.004. Forε=0.008,one can see thatσ(t) does not grow with time with a period of time. It suggests that even the high frequency modes are frozen for a period of time. Afterwards,σ(t)grows continuously with time.Forε=0.004,σ(t)keeps unchanged even up tot=1010.σ(t)no longer displays a power law for the FPUT system with periodic boundary conditions in the very weakly nonlinear regime. Therefore, we cannot obtain the values ofteqthrough relatively short time scales for very weak nonlinearity throughσ(t). The scaling law for the FPUT system with small number of particles for periodic boundary conditions in the very weakly nonlinear regime remains a very difficult problem.

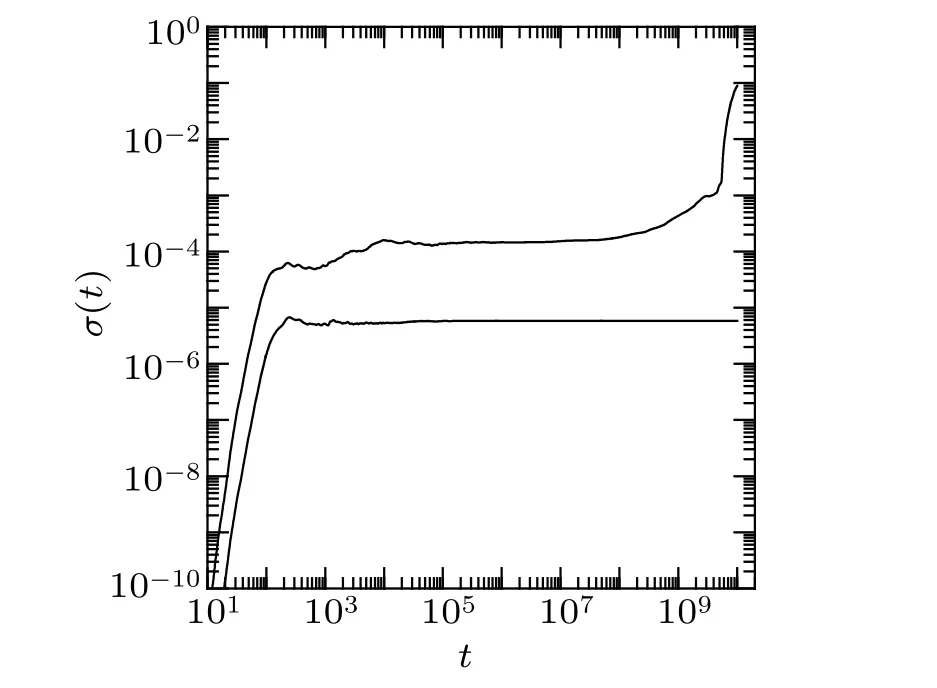
Fig. 6. The results of σ(t) depending on t in log–log scale for α-FPUT model. The curves from top to bottom at t =106 are for ε =0.008, and 0.004,respectively.

4. Conclusion

In this paper, we studied numerically the behaviors of thermalization in the range of weak nonlinearity forα-FPUT model andβ-FPUT model withN=32. We find the scalingteq∝ε−4,which has been observed in Refs.[42,43],is only established within a certain range of nonlinearity for both models. In this range of nonlinearity, energies can transfer from the initial excited modes to other modes continuously. This energy transport process happens via the nontrivial six-wave resonances,which hence lead toteq∝ε−4. With a further decreasing nonlinearity, a crossover fromteq∝ε−4to a steeper growth will appear. Energies are found to be frozen on low frequency modes for large time scales in the very weakly nonlinear regime, which indicates that the resonant wave–wave interaction theory no longer works in the very weakly nonlinear regime. In this case, redistribution of mode energies happens through the resonances of the high frequency modes,which lead to the deviation from the scaling lawteq∝ε−4.Finally, we stress that the scaling law for the FPUT system with small number of particles for periodic boundary conditions in the very weakly nonlinear regime remains a very difficult problem. We hope our work can be useful in motivating more studies in this direction.