Fine-grained uncertainty relation for open quantum system∗
Shang-Bin Han(韩尚斌), Shuai-Jie Li(李帅杰), Jing-Jun Zhang(张精俊), and Jun Feng(冯俊)
School of Physics,Xi’an Jiaotong University,Xi’an 710049,China
Keywords: open quantum system,fine-grained uncertainty relation,Unruh effect
1. Introduction
Since it was originally proposed by Heisenberg in 1927,[1]the uncertainty principle has been a subject of recurring interest for over ninety years. The principle bounds our ability to simultaneously predict two incompatible observables of a quantum particle,thus distinguishing the quantum world from its classical complement. Nowadays, it has been recast,in an information-theoretical framework,with the uncertainty quantified by entropic measures,[2–4]and has many important applications in entanglement witnesses,[5–9]quantum metrology,[10]quantum cryptographic protocols[11,12](see Ref.[13]for a recent review).
However, even entropic formula of uncertainty principle is fairly useful in various cases,it is still a rather coarse way of measuring the uncertainty of a set of measurements. In particular,one cannot distinguish the uncertainty inherent in obtaining any combination of outcomes for different measurements,since an entropic function can only encode the probability distribution of outcomes as a whole. To overcome this defect,Oppenheim and Wehner proposed a new form of uncertainty relation,i.e.,a fine-grained uncertainty relation(FUR).[14]For a set of measurementsT={t},associating with every combination of possible outcomesx=(x(1),...,x(n)), there exist a set of inequalities

whereB×nis the set involving all possible combinations of outcomes,p(t)is the probability of choosing a particular measurement,andp(x(t)|ρ)is the probability that one obtains the outcomex(t)after performing measurementton the stateρ.To measure the uncertainty, the maximum in functionζx=maxρ∑nt=1p(t)p(x(t)|ρ)should be evaluated over all states allowed on a particular system. It is easy to tell that one cannot obtain outcomes with certainty for all measurements simultaneously whenζx <1. Like entropic formula, the FUR can also be used as an entanglement witness in practice.[15]
On the other hand, FUR becomes an important link part between various disparate subfields. For instance, in their original work,[14]Oppenheim and Wehner showed that FUR can determine bipartite quantum nonlocality through a nonlocal retrieval game, and further discriminate among classical,quantum,and superquantum correlations involved in a multipartite system.[16,17]Based on FUR, a steering inequality has been given to capture bipartite Einstein–Podolsky–Rosen steering from both theoretical and experimental views.[18,19]Similar to entropic uncertainty, a quantum-memory-assisted FUR is proposed to improve the lower bound of inequality,which may benefit quantum cryptography.[20]Moreover, a profound link between the FUR and thermodynamics has been found,[21,22]which claims that a violation of uncertainty relation implies a violation of second thermodynamical law.
While most studies focus on closed systems,a complete account of FURs requires understanding them for open quantum systems,due to inevitable decoherence or dissipation from the interaction between systems and environment in any realistic regime. In particular,such environment decoherence limits the ability and task quality in various quantum computation protocols. In recent years, particular interests have been attracted for an accelerating quantum system through an external field.[23–25]Even when the environment in its vacuum state,it is known[26]that quantum system can be spontaneously excited as if it was in a thermal bath with temperatureT=a/2π,proportional to its proper acceleration. This celebrated Unruh effect is a key piece of the jigsaw for combining both relativity and quantum physics,[27]which provides a strong motivation to measure it and related phenomena in the laboratory. However, given the difficulty of direct observation (one needs an acceleration of about 1023m/s2to reach room temperature),alternative approaches using cutting-edge quantum technology have been developed. For instance, with significant influence of Unruh decoherence on practical quantum information tasks, it may be possible to measure indirectly the Unruh effect on localized quantum systems, which in principle can be measured, transformed and exploited for quantum information tasks.[28,29]In particular,for the localized detector as an open system,its Berry phase[30]and entanglement[31–33]depend sensitively on Unruh temperature,thus have been suggested to be good probes on Unruh effect.For qubits restricted in moving cavity,entropic uncertainty bound[34]and FUR[35]as the entanglement witnesses were also investigated,showed a significant modification attributed to the(relativistic)motion status of system may happen. On the other hand, it was suggested to employ a quantum simulator to recreate a synthetic Unruh effect in the laboratory by Bose–Einstein condensate(BEC),[36]NMR,[37]and superconducting circuits,[38]etc.
In this paper, we explore FUR for open quantum system under relativistic motion, and find the uncertainty bound does depend on the motion state of the system. We work in the detector-field picture and study a localized system composed of multi-Unruh–De Witt detectors(UDD)in Minkowski space, each modeled by an accelerating two-level atom. Assuming a weakly interaction with a bath of fluctuating scalar field, the detectors behave like an open quantum system, suffering from an environment decoherence attributed to thermality of Rindler vacua,a manifestation of the Unruh effect.Without loss of generality,we particularly focus on two typical scenarios with single-UDD and two-UDD respectively. For a single detector,the Unruh effect is manifested by purely environment decoherence, which forces the state of detector into approaching an equilibrium thermal state. Once estimating the FUR uncertainty boundζfor the single detector,we show an increased uncertainty in quantum measurement would be induced, which is a direct result of Unruh decoherence. On the other hand,for a multi-detectors system,it was known[23]that the quantum correlation could be generated through its Markovian evolution. With this novel feature of the multipartite open system,the Unruh decoherence may be overcome in certain conditions. To demonstrate it,we particularly study the FUR for a two-UDD system and find that the uncertainty bound can be protected from the Unruh effect, due to the intrinsic correlation generated under the relativistic motion. For a general case withn-UDD(n >2),one may expect that a similar reduced Unruh decoherence could also exist,[39]as ann-UDD system shares the same collective correlation dynamics like a bipartite system but can only be calculated numerically.
The paper is organized as follows. In Section 2, we solve the master equation of multi-UDD system, and give explicitly its density matrix. In Section 3, we evaluate the FUR for single-UDD and two-UDD system respectively, and show that how the uncertainty bound of FUR can be modified by Unruh effect. In Section 4, the summary and discussion are given. Throughout the paper, we use natural units withG=c==kB=1.
2. Master equation of accelerating qubits
To proceed, we first recall the full dynamics of multi-UDD state in flat spacetime,which effectively is governed by a Lindblad master equation. Without loss of generality, the total Hamiltonian of the combined system (detectors + environment)is

HereHn-atoms is the Hamiltonian ofn-UDD in the common comoving frame, each modeled by a two-level atom with energy level spacingω.HΦis the standard Hamiltonian of free massless scalar fieldsΦ(x), whose details do not need to be specified in our approach.[23]For later convenience,we particularly considern=1,2 cases. Since each atom internal dynamics is driven by a 2×2 matrix,we choose Hamiltonian of UDDs in a concise form as

To derive the dynamics of detectors’state,a separable initial state of total system is assumed,i.e.,ρtot=ρn-atoms(0)⊗|0〉〈0|, where|0〉is the vacuum state of fieldΦ(x). Then, in a weak coupling limit, the Markovian dynamics of detectors’density matrix can be induced fromρtot(t),by tracing over all field degrees of freedom,i.e.,ρn-atoms(t)=TrΦρtot(t). This just means that in the limit of weak couplings,the changes in the evolution of the system occur on very large time-scales,that the details of the internal environment dynamics of the scalar fieldΦbecome irrelevant. The detectors’ density matrix now satisfies a master equation in Kossakowski–Lindblad form[41,42]


Substituting Eq.(8)into the master equation(4)and assuming that the initial state of the atom is|ψ(0)〉=cos(θ/2)|+〉+sin(θ/2)|−〉, one can easily work out the time-dependent reduced density matrix
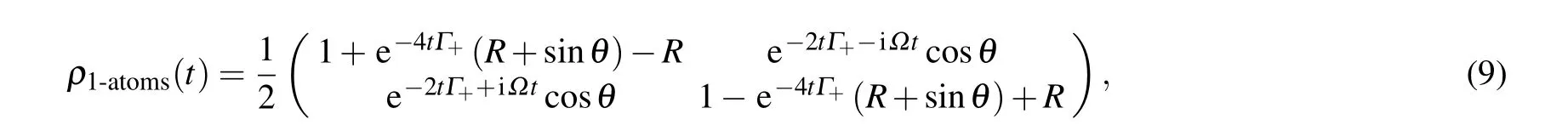
where a ratioR ≡Γ−/Γ+is defined,and frequencyωis renormalized toΩby Lamb shift.[23]
For a two-atoms system,the Bloch representation of its density matrix becomes

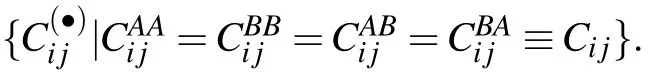

One can observe that the final equilibrium state of 2-atoms system now depends on the ratioR=Γ−/Γ+characterizing the scalar bath,as well as the choice of the initial state encoded inτ=∑iii(0),a dimensionless constant of motion satisfying−3 ≤τ≤1 to keepρ2-atoms(0)positive.
3. FURs for open quantum systems


Substituting the Wightman function back into Eq.(7),we obtainΓ+= (ω/4π)[(eβω+1)/(eβω −1)],Γ−=ω/4π, andR=(eβω −1)/(eβω+1)(apparently,Ris a monotonic function of accelerationa,e.g.,R=0 for infinity acceleration,andR=1 fora=0) withβis the inverse of Unruh temperatureβ ≡1/T=2π/a, from which the explicit form of Eqs. (9)and (11) are obviously. With all these results, we are sufficiently prepared to study the FUR for these localized quantum systems.
3.1. FUR for accelerating qubit
We now evaluate the maximum of FUR (1) with uncertainty bound read asζx=maxρ∑nt=1p(t)p(x(t)|ρ). For simplicity, we consider two projective measurements with two outcomes,e.g., in eigenbasesX ≡σx={0x,1x}andZ ≡σz={0z,1z}, whose eigenstates in common convention are{|+〉,|−〉}and{|0〉,|1〉}, respectively. Assuming each measurement is chosen with probability 1/2, the FUR (1) can be rewritten as
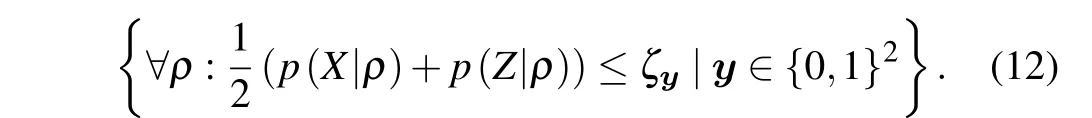
For instance,for any pure state,it is known[21]that
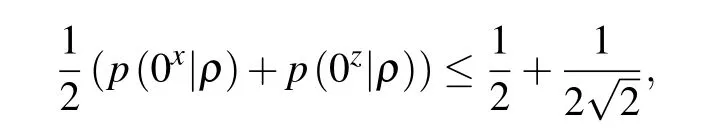
which is also hold for all other pairs of outcomes(0x,1z),(1x,0z), and (1x,1z). In particular, we call those states that saturate a particular inequality are maximally certain states(MCS).

From the density matrix Eq.(9),we can calculate straightforwardly the measurement probability for the outcomes(0x,0z),

For a uniform accelerating detector at a fixed time,its density matrix depends on different initial state preparation by parameterθ. This means that, to obtain the maximum of the lefthand side of FUR,we should evaluate it for allθ ∈[0,2π]. We can now write the uncertainty bound explicitly

whereΓ+andRhave been given before,which depend on the detector’s accelerationaand evolution timet. By extending the above calculation for other possible pairs of outcomes,like (0x,1z),(1x,0z),and (1x,1z), we obtain three other uncertainty bounds
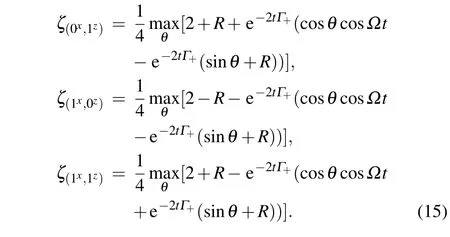
After substituting the explicit representations ofΓ+andRderived before into Eq.(15),we can depict four FUR uncertainty bounds in Fig.1.


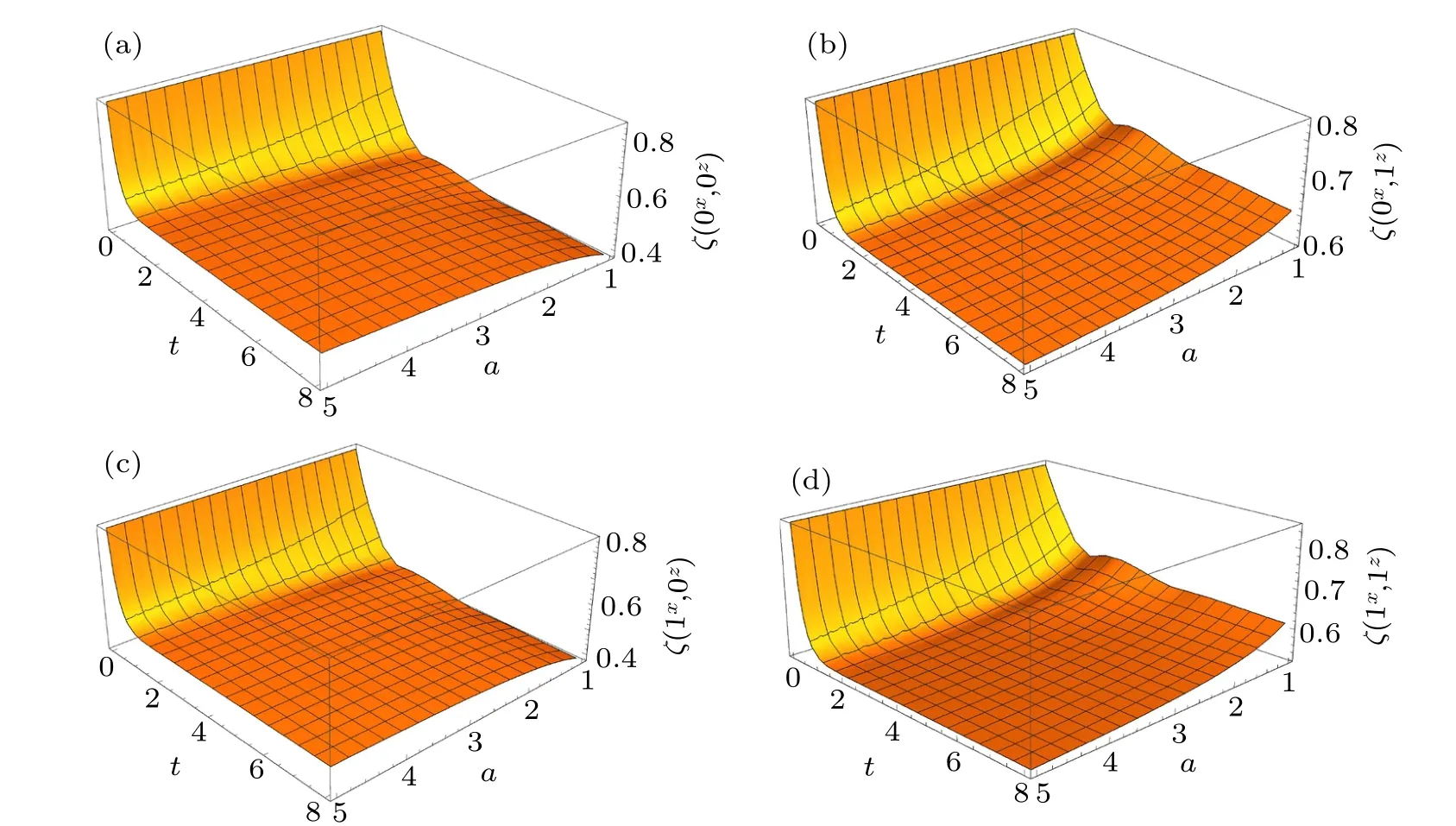
Fig. 1. The FUR uncertainty bound ζ for pair measurement outcomes (a) (0x,0z), (b) (1x,1z), (c) (0x,1z), (d) (1x,0z), respectively, and all of which are the functions of detector’s acceleration a and time t. With larger acceleration a, a greater Unruh decoherence is triggered, inducing a nontrivial modification on the uncertainty bound ζ. For simplicity, we adopt the parametrization in natural units as in Ref. [29] and evaluate both uncertainty bounds for Ω =1.
3.2. FUR for accelerating two-atoms
For the case of a bipartite system of UDD, each modeled by a two-level atom, the upper bound on their FUR has a profound link with quantum nonlocality between atoms. In particular, by displaying a nonlocal retrieval game, the FUR uncertainty bound can discriminate different theories with the help of Bell-like inequalities.[14]On the other hand, it is known[23,45]that nontrivial quantum correlation can be generated through the competition between Unruh decoherence and the Markovian dynamics of the system. Therefore, we expect that a similar modification on FUR uncertainty bound may also exhibit under the relativistic acceleration.
Let us recall that how to display the nonlocal retrieval game proposed in Ref.[14]on the two-atoms system.According to the game, Alice and Bob receive questions“s”and“t”with some probability distribution,e.g.,p(s,t)=p(s)p(t),and their answer“a”or“b”will be winning answers determined by the set of rules. In the prescribed game,Alice and Bob receive respective binary questionss,t ∈{0,1}, and win the game if their respective outcomesa,b ∈{0,1}satisfya⊕b=st.Then,the probability of winning the game for a physical theory described by bipartite stateρ2-atomsis given by
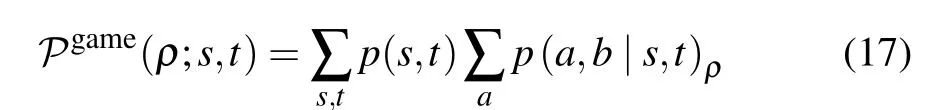
with
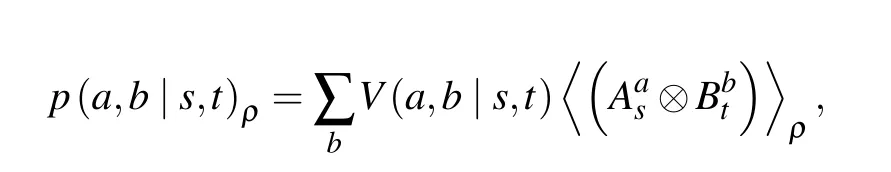
whereAasandBbtare projectors of observablesandtwith outcomeaandb, could beAas= [I+(−1)as·σ]/2 andBbt=[I+(−1)bt·σ]/2 respectively. The condition function is given asV(a,b|s,t) = 1(iffa ⊕b=st). Givenp(s,t) =p(s)p(t)=1/4, it was shown that the FUR can be expressed in terms of the maximum winning probability of prescribed retrieval nonlocal games,and the degree of nonlocality of the underlying physical theory.Therefore,we have an FUR bound like[16]

which indicates that〈ℬmax〉ρ2-atomsshould depend on the initial state of detectors labeling byτand system’s accelerationa.
For different values of acceleration,we need to select the two largest eigenvalues in{λ1,λ2,λ3},that gives the probability of winning the retrieval game

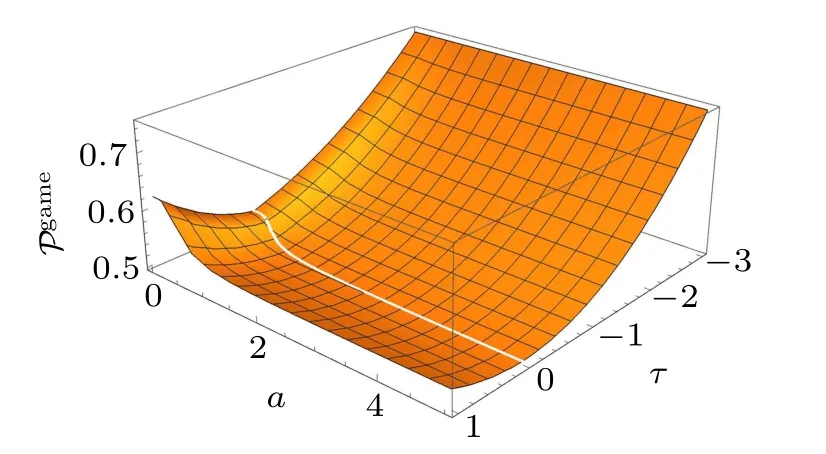
Fig. 2. The probability of winning the retrieval game Pgame as a function of detectors’ acceleration a and the initial state preparation characterized by the dimensionless constant τ=∑iii(0)satisfying −3 ≤τ ≤1 to keep ρ2-atoms(0)positive. One can observe that the maximal value of Pgame can reach for initial state satisfying τ =−3. For simplicity, we adopt the parametrization in natural units as in Ref.[29]and evaluate both uncertainty bounds for Ω =1.
4. Conclusion

- Chinese Physics B的其它文章
- Coarse-grained simulations on interactions between spectrins and phase-separated lipid bilayers∗
- Constraints on the kinetic energy of type-Ic supernova explosion from young PSR J1906+0746 in a double neutron star candidate∗
- Computational model investigating the effect of magnetic field on neural–astrocyte microcircuit∗
- Gas sensor using gold doped copper oxide nanostructured thin films as modified cladding fiber
- Exact explicit solitary wave and periodic wave solutions and their dynamical behaviors for the Schamel–Korteweg–de Vries equation∗
- Suppression of ferroresonance using passive memristor emulator

