在数学课堂中提高学生的多维度思维能力的措施

戴云婷

（南京师范大学附属中学新城小学北校区，江苏南京 210000）

一、学生的思维能力概况

在小学数学学习中，由于受到各种因素的影响，学生的学习能力各有不同。一部分学生对于新授知识的接受能力较强，作业完成质量也较高；而另一部分学生在数学学习过程中的理解能力较弱，难以快速掌握新授知识，不能很好地学以致用。这一类学生在学习数学时是比较吃力的。此时，教师如果能够注重对学生数学思维能力的培养，则能在很大程度上帮助那些数学知识接受能力较弱的学生。

在小学数学的教学过程中培养学生的数学思维能力，一方面能帮助学生整合自己已经学到的知识；另一方面能让学生对思维拓展类题目产生自己的理解。

数学思维是数学学习中独特的思维，根据“数学三个世界”学习理论，直观行动思维、具体形象思维、抽象逻辑思维这三种思维之间的关系，并不是简单的替代关系，而是替代与共存辩证统一的关系。小学阶段的学生以直观行动思维、具体形象思维为主，但要想进行深度教学，教师还应关注学生的抽象逻辑思维。在教学过程中，教师需要根据不同年龄段学生的需要和知识的侧重点，选择合适的教学方法，以促进学生思维能力的发展。

二、提高学生数学思维能力的措施

（一）触发直观思维，促使学生深度理解

理解能力本质上是个人把握事物的能力，数学理解能力即准确把握数学知识的能力。如果学生能在深度理解的基础上记忆相关知识，则其也能很好地关联各个知识点，并在以后的教学情境中加以运用。这里所说的深刻理解不是指单纯的抽象思考，因为小学生的抽象思维能力有限，如果教师一味地要求学生对知识进行抽象理解，很容易造成误解，让学生对学习失去兴趣。教师在教学的过程中，应注重培养学生的直观思维能力，可以通过数形结合、情境代入等方式，触发学生的直观思维，让学生更容易地理解数学知识，实现从抽象到具体、再回到抽象的思维升华过程。

例如，在“平行四边形的面积”一课的教学中，教师要求学生单纯地记忆平行四边形的面积公式（用平行四边形的底乘以高）是易如反掌的，但要想让学生彻底地理解为什么用平行四边形的底乘以高，还需借助几何知识，让学生自己动手试一试。因此，教师在讲授这部分知识点时，应该让学生提前剪出一个平行四边形，使其在剪、移、拼的操作中，充分地感受平行四边形可以转化成我们熟悉的长方形，此时，平行四边形的底相当于长方形的长，平行四边形的高相当于长方形的宽，所以平行四边形的面积可以通过用平行四边形的底乘以高来得出。

数学家希尔伯特曾说，对数学的认知能力第一时间来自直观感受，这种感受到感知的过程是对空间数量关系的认知过程。小学生正处在思维认知的发展阶段，在这一阶段，学生对事物的探索欲是比较强烈的，因此教师在授课中需要让学生充分地观察和感受，突出问题的直观形象，由此触发学生的直观思维，这种教学方式不仅能激发学生学习数学的兴趣，降低其理解数学知识的难度，还能让学生在主动探索、主动操作中理解并运用数学知识。

（二）引发类比思维，促进学生融合理解

在小学数学的学习过程中，学生能够发现，许多数学知识能够紧密地联系在一起，数学规则与其根本性质其实是相通的。教师在教学数学知识的过程中，要把握好知识点的内在联系，将所学的新知识与之前学习过的内容联系起来，通过类比的方法，让学生理解其中的本质，在建立新概念的同时，形成知识网络。

以苏教版《数学》五年级上册“多边形的面积”为例，在复习时，我们可以提出两个问题让学生提前思考：①简要回顾各种图形面积的计算推导过程；②找出各个图形面积计算公式之间的联系。学生的回答如下所示。

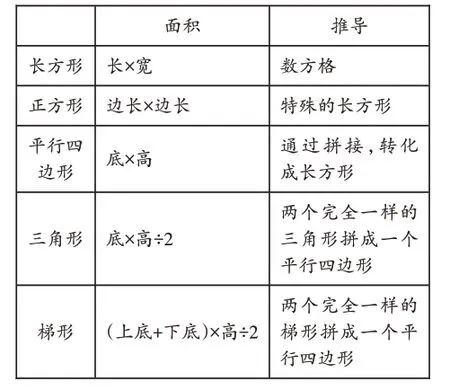
图1

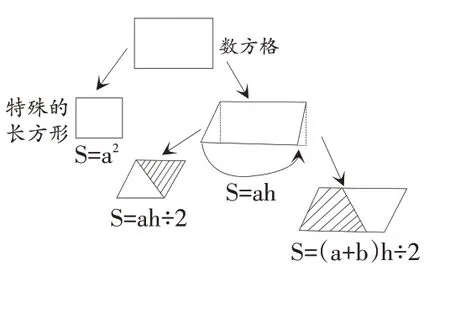
图2

我们可以看到，学生提供的答案体现了两种方式：一种是列表式；另一种是思维导图式。这两种方式在进行知识点的复习时，都是十分常见且重要的。不管哪种方式，我们都能看出，在学习四边形的面积公式时，我们是将图形类比成长方形，用长方形的面积公式来推导的，而三角形、梯形的面积公式则是类比成平行四边形，进行推导的，也就是说，我们所学的新知识可以类比成我们之前学过的知识。

结合学生的心理、年龄特征及其认知发展水平，我们知道学生在理解或记忆新知识时，往往会感到困难。如果教师在教学过程中能够引发学生的类比思维，将新知识与之前学过的类似内容联系起来，就可以间接地推导出学生所要学习的新知识，这样不仅能让学生回顾、巩固所学过的旧知识，还能降低学生理解新知识的难度，从而让学生更加充分地理解所要学习的新知识。

（三）启发求异思维，促进学生深入思考

在小学数学课堂中，问题情境的创设司空见惯，但是很多教师依然停留在“怎么教”的阶段，对于“教什么”缺乏深入的理解，这使教师在设置问题时更多地停留在知识的表面，教学问题往往停留在追求结果的阶段，缺乏对问题的深入思考。对此，教师可以通过追问的方式，发展学生的逆向思维能力，深化学生对教学内容的理解。

例如，在教完多边形面积这一单元时，教师可以布置这样一道练习题：王大伯家有一块地，政府规划一条大路经过这块地，政府征地后王大伯家的这块地还有多少平方米？

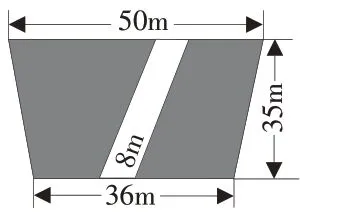
图3

在计算这道题时，大多数的学生是利用梯形的面积减去中间平行四边形的面积来求出阴影部分的面积。在学生想出这样的方法后，教师可以继续追问：“还有其他方法吗？”只有几个学生举起了手，其中一个同学站起来，用手比画着说：“其实我们可以将这个图形进行‘压缩’，此时阴影部分组成了一块梯形，而这一梯形的上底边和下底边之和正是原来梯形的上底边与下底边之和减去16，高依旧是原来梯形的高，所以面积就能更简便地计算出来了。”这时，同学们恍然大悟，回过头来看，这样的方法并不难，它不仅比原来的方法更简便，还更易于学生理解这种题型。

通过这样的问题，教师可以引导学生用不同的方法来解决问题，让学生在求同存异中不断进步，掌握利用多种方法来解答难题的技巧，同时，学生的思维也得到了一定的拓展。在当前的教学模式中，教师要想培养学生的创新精神和创造能力，就应更重视对学生数学思维的培养，启发学生去创新。在小学数学教学的过程中，教师应引导学生一题多解，调动学生的学习兴趣，让不同层次的学生有机会去思考，也能让学生养成灵活多变的思维能力。

多维度思维的培养，不仅能让学生更好地理解数学知识，提高其计算能力，还能培养学生内在的数学能力，让学生在碰到数学问题时，能通过多维度思维的引导，接受并理解新知识，将新知识与旧知识联系起来，形成自己的数学知识网络，从而加深对知识的理解，同时，这也培养了学生发现问题、分析问题、解决问题的综合能力。这样的深度数学理解目标与核心素养的构建不谋而合。

因此，在小学数学教学中，教师可以从发展学生思维的角度出发，结合数学核心素养的基本要求，为学生设计问题型课堂，让学生能在课堂中获得知识，同时获得学习知识的能力，为其终身发展奠定基础。