物流配送路线的数学建模

邓上煜，徐艳，谢康

（四川大学锦城学院 计算机与软件学院，四川成都，611731）

1 课题背景

数学模型是一种抽象模拟现实世界的过程，它能通过模拟演算解释现实世界的某些客观现象、发展规律，进而对现实世界的某个事件或发展提供某种好的策略。数学建模是当代大学生在未来工作和生活中探索各种各样问题并寻求解决方案的一个非常有帮助的工具。本文将选取现实生活中物流配送路线选择作为场景实例进行数学建模并求解最佳方案。

2 问题描述

配送网络图（图1）中P为配送中心，其余A-I为客户的接货点，各边上的数字为公里数，括号内的数字为需输送到各接货点的货物量，单位为吨。有装载重量为2吨和5吨的两种货车，车辆一次运行路线距离不超过35公里，每个派送点只由一辆车服务一次，车辆由配送中心出发，完成任务后返回配送中心，快递车辆配送过程中无装货，只考虑卸货。每个点卸货时间固定为5分钟，车辆每小时行驶距离为10千米，每个派送人员工作时间为8小时。

图1 配送网络图

本文拟采用数学模型确定最优配送方案评估标准，并将图中所有点配送完毕。选择最优运输路径，使成本最小化，配送订单最大化，满载率最大化的方式制定配送运输方案。

3 问题分析

设车辆行驶速度为V(km/h)；卸货时长为Tx(h)；货车载重为W(t)；单个派送员单日工作时长为Ty(h)。

将单次多个点配送时长定义为单次时长t（h）；单次配送多个点行驶距离定义为单次行驶距离s（km）。假定要进行n次配送，ti、si分别为第i次配送的单次配送时长和单次配送行驶距离，则总时长T（h）的计算公式：

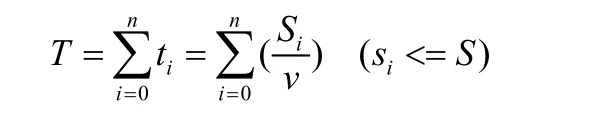
将单次配送任务的总货物量定义为单次货物量w（t），单次货物量与车辆载重之比定义为单次满载率k，所有单次满载率加和除以配送次数得到平均满载率K。假定要进行n次配送，wi、ki为第i次配送的单次货物量和单次满载率，则K的计算公式：

将单次配送任务的配送点数量定义为单次订单量l（个）。从所有单次订单量加和除以配送次数得到的平均订单量L（个）。假定要进行n次配送，li为第i次配送的单次订单量，则L的计算公式：

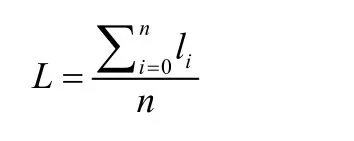
根据整理出的信息将此问题中的成本定义为两个方面，第一是车辆成本、第二是资源成本。

（1）车辆成本与大型货车和小型货车各使用次数有关，拟制定一个车辆成本指标指标U用于表示车辆使用情况。下面假设大车使用了x次，小车使用了y次，基于运载量给出U的计算公式：

（2）通过信息整理分析，单次配送最大耗费时长为 S/v=3.5(h)加上卸货时长Tx之和，假设单次配送中总卸货时长不超过0.5h，则单次配送最大耗费时长为4h，若配送点过多导致卸货时长超过0.5h，则认为配送点过于密集，可以将密集的配送点整合为一个快递服务站来保证单次配送总卸货时长再0.5h内，该问题非时效指标计算的关键点，所以整合操作在本文中不作重点考虑。

用单次配送实际耗费时长除以4h则可以理解为单次配送的时间利用率，定义为单次时效o，从所有单次时效相加求平均时效O，以反映员工的时间利用率。假定要进行n次配送，oi为第i次配送的单次时效，下面给出O的计算公式：

4 建立数学评估模型

4.1 设定总体评估指标

K、L、O、T、U中每个评估指标都不能单独的确立某个方案为最优解，故设定一个总指标sum作为对所有评估指标的综合考量用于的评估。由问题分析得出以下结论：在最优解与评估指标的关系中K、L、O为正相关， T、U为负相关。本文将K、L、O分别乘以某个权值a、b、c之和再减去T、U分别乘以某个权值d、 e之和作为总指标sum的综合值，以公式表示为：

该sum值即可作为方案的总体评估指标，sum值越大则方案越优。

4.2 查找全部“相邻点连线”

找出除源点P外所有点的排列组合方式，将每一个排列组合的字符序列看作是一条行驶路径，在这条行驶路径的配送点序列中，验证从头到尾任意前后两点之间是否都存在直连通路。若存在任意前后两点之间不为通路的情况则去除该行驶路径，否则该通路保留，并在本文中将这样的路径称为相邻点连线。这样的步骤作为初步筛选，保证了单次配送的各配送点都是相互紧挨着的，是对最优路径的初步选择。

4.3 相邻点分区

经过初步筛选后，保留下来的行驶路径均为相邻点连线，然后可对所有保留下来的相邻点连线进行分区。

以图1举例说明相邻点分区的方法：从I点开始向前查找到下一个点A，I、A两点的货物的总量小于车辆载重5，并且从P点到I点再到A点再回到P点的最短总路程小于35，则继续向前查找到下一个点B，并继续向前做同样的验证，直到点D的时候货物了大于5，则退回将I、A、B、C划为一个分区。然后再从D点开始做以上同样的操作，最终可以得出一个分区方案。

在找出相邻点连线的基础上，通过相邻点分区的方式，我们可以得到所有初步最优的分区方案，并且在每一个方案的每一个分区中，通过相邻连线保存的行驶路径即可直接找到配送该分区的区内最佳行驶路径，即对每一个分区只需要考虑源点到每个分区的起点和

终点的最短距离，避免了分区内部最优路径的选择问题。

通过这种方式，找出一种分区分案和一条相邻连线，即可以比对某一种分区方案制定一个整体最优的配送方案。计算并保存所有分区方案的数据，将这些数据根据熵值法进行数学评估模型的设计。

5 计算过程

5.1 总体数据

利用 Dijkstra算法计算出所有配送方案的数据，如图2所示。

图2 利用 Dijkstra算法计算出所有配送方案的数据

5.2 熵值法

根据各项指标的变异程度，利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据，即可采用熵值法对各权值a、b、c、d、e进行计算求值。

将以上数据集中各方案的五个评估指标值转换为一个22行5列的矩阵A，表达式如下：

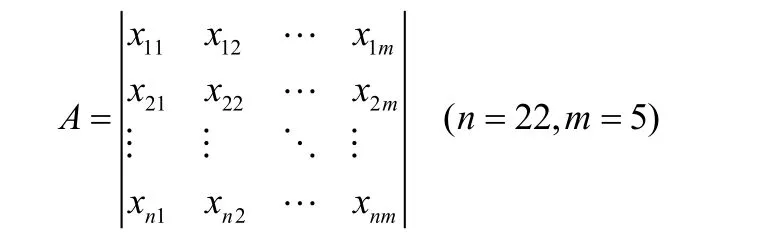
将矩阵A转换为如下决策矩阵B：

基于熵值法，第j个属性下第i个方案，pi的贡献度以dij表达式表示为：

基于熵值法，所有方案对属性xj的贡献总量ej的值也就是各评估标准的熵值，当某个属性下各方案的贡献度趋于一致时，ej将趋于最大值1。当ej值为1时，就可以不考虑该属性在决策中的作用，即该属性的权值为0。

再将dij矩阵带入ej中即可得到五个评估指标的熵值大小，分别为 ：K：0.9985426；L：0.99665695；O：0.99936664；T：0.99864525；U：0.998687。

最终求得sum值大小作为评估指标的数学评估模型即为：

5.3 得到最优解

将各个指标的权值带入模型中，再次利用Dijkstra算法并遍历所有方案找出sum值最大的方案，即为最优解。输出结果如图3所示。

图3 输出结构图