基于局部搜索BLPSO 算法的动态经济调度优化

唐 柯

（江苏大学电气信息工程学院，江苏镇江 212013）

0 引言

动态经济调度（Dynamic Economic Dispatch，DED）是电力系统中最实际且最有意义的问题之一，具有非线性、非凸性和高维度等特点。DED 问题的优化目标是各机组在约束条件下运行且满足负载需求时，其总燃料费用最低。与传统静态经济调度相比，DED 考虑的约束更加复杂，其调度策略更加符合实际，但求解难度也更大。

许多传统优化算法被用来解决DED 问题，包括非线性规划法［1］、动态规划法［2］、梯度算法［3］以及拉格朗日松弛法［4］，这些方法高度依赖初始解质量，并且要求待处理问题是连续可微的。由于阀点效应、爬坡约束、禁止操作区域约束等约束的存在，使得DED 问题具有非线性、非凸性等特征。因此，这些方法得到的解不能保证是全局最优解。

过去十多年里，启发式算法得到了广泛研究并应用于数据挖据［5］、人工神经网络［6-7］和轨迹优化［8］等领域。启发式算法全局搜索能力强，适合求解非线性、不可微的优化问题，因此被用于求解DED 问题。如Gaing［9］利用经典粒子群算法（Particle Swarm Optimization，PSO）解决DED 问题，在6 机组与15 机组的DED 问题上验证了该算法性能；Meng等［10］利用纵横交叉算法（Crisscross Optimization，CSO）解决大规模DED 问题，该算法通过两个相互作用的水平算子和垂直算子产生高质量的解；Mohammadiivatloo等［11］利用帝国竞争算法（Imperialist Competitive Algorithm，ICA）解决DED 问题，ICA 算法属于多种群结构算法，求解效率高，但算法性能依赖于参数选取，计算成本也较高；Arul 等［12］利用混沌自适应差分和谐搜索算法解决DED 问题，在该算法中将和谐搜索的纵向调节算子替换成混沌差分变异算子，提升了算法处理高维度问题的性能；Hemamalini 等［13］利用人工免疫系统算法（Artificial Immune System，AIS）解决DED 问题，实验结果表明，AIS 算法在求解质量和计算能力方面有着很强的鲁棒性；Zou 等［14］利用全局记忆差分进化算法（Memory-based Global Differential Evolution，MGDE）解决DED 问题，实验结果表明，与现有算法相比，MGDE 取得的最优解精度大大提高；Zaman 等［15］利用遗传差分混合算法解决DED 问题，该算法采用自适应机制，能够适应不同复杂程度的问题；Elattar［16］利用混合细菌觅食遗传算法（HGABF）解决DED 问题，该算法将细菌觅食算法与遗传算法相结合，弥补了细菌觅食算法收敛性差的缺点。

然而，在现有文献中，针对含电动汽车的动态经济调度问题的研究还不深入，所得最优解精度不高。针对这一情况，本文提出一种基于观察蜂局部搜索的生物地理粒子群算法（Biogeography-based Learning Particle Swarm Optimization with Onlooker Bee Search，BLPSO-OBS）。该算法采用生物地理粒子群更新策略与观察蜂局部搜索策略，提升了收敛速度与求解精度，实验结果证明了该算法在求解含电动汽车的动态经济调度问题上的高效性。

1 含电动汽车的动态经济调度问题

DED 问题的优化目标是各机组在约束条件下运行并且满足负载需求时，总燃料费用最低。本文考虑的DED 问题含电动汽车负载，因此比传统的DED 问题更加复杂。

1.1 目标函数

DED 问题的燃料成本函数是火力发电机组的二次燃料成本方程，公式为：

其中，Ng是发电机组总数，T是调度时段数量，Fjt(Pjt)是第j个发电机组在第t个调度时段内的消耗，Pjt是第j个发电机组在第t个调度阶段的实际输出，aj、bj、cj、dj、ej是第j个发电机组的燃料成本系数，是第j个发电机组的最小发电限制。

1.2 发电约束

1.2.1 电力平衡约束

在每一个调度时段，发电机组产生的总功率应等于负载总需求功率和传输网络总消耗的和，即：

其中，PD,t是调度时段t内的负载总需求功率，PL,t是调度时段t内的传输网络总消耗，Lev,t是调度时段t内的电动汽车负载需求。电动汽车负载分配的详细描述见1.2.5 节。

在调度时段t内的传输网络总消耗可采用以下公式计算：

其中，Bji、Bj0、B00是损耗系数。[Bji]可看作一个Ng×Ng的矩阵。

1.2.2 发电能力约束

在每一个调度时段内，每个发电机组的发电功率应在其最小与最大输出功率之间，即：

1.2.3 爬坡约束

发电机启动和关闭的物理限制施加了爬坡约束。机组发电量增加的限制如下：

同样，机组发电量减少的限制如下：

其中，Pj,t-1是第j个发电机组先前的输出功率，URj、DRj分别是第j个发电机的上升斜坡极限和下降斜坡极限。

1.2.4 禁止操作区

禁止操作区域是由于蒸汽阀操作或轴承中的振动引起的。第j个发电机的可行工作区描述如下：

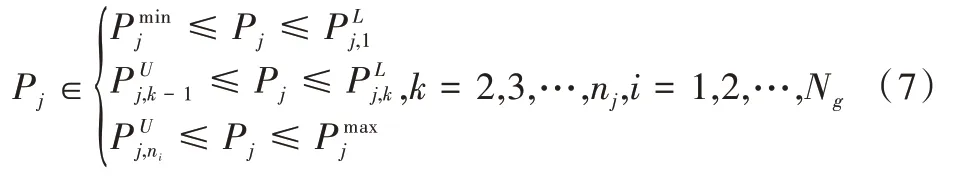
其中，nj是第j个发电机组的禁止操作区域数量，分别是第j个发电机第k个禁止区域的下限与上限。

1.2.5 插入式电动汽车负载

插入式电动汽车对功率要求很高，与传统的家庭和工业负载不同，其同时对20kW 家用充电器和120kW 增压器进行充电，可能会在每日功率需求曲线上形成巨大的波动甚至尖峰。为避免这种影响，本文提出了EPRI、OFFPEAK、PEAK、STO 4 种充电模式［17］。4 种充电模式负载分布情况如表1 所示。

4 种不同的充电模式规定了负载需求在不同调度时段内的分配情况，将在电力需求约束中施加额外负载。在考虑了以上4 种模式后，使得DED 问题受到严格限制，并且显示出很强的非凸性，需要更有效的算法来解决该问题，这也是本文提出新算法的目的所在。

2 基于局部搜索的生物地理粒子群算法

2.1 PSO 算法

PSO 算法是一种基于种群的元启发式算法，最早由Eberhart 等［18］提出。PSO 算法基于群体智能理论，其基本思想是通过群体中个体之间的合作与信息共享找到最优解。

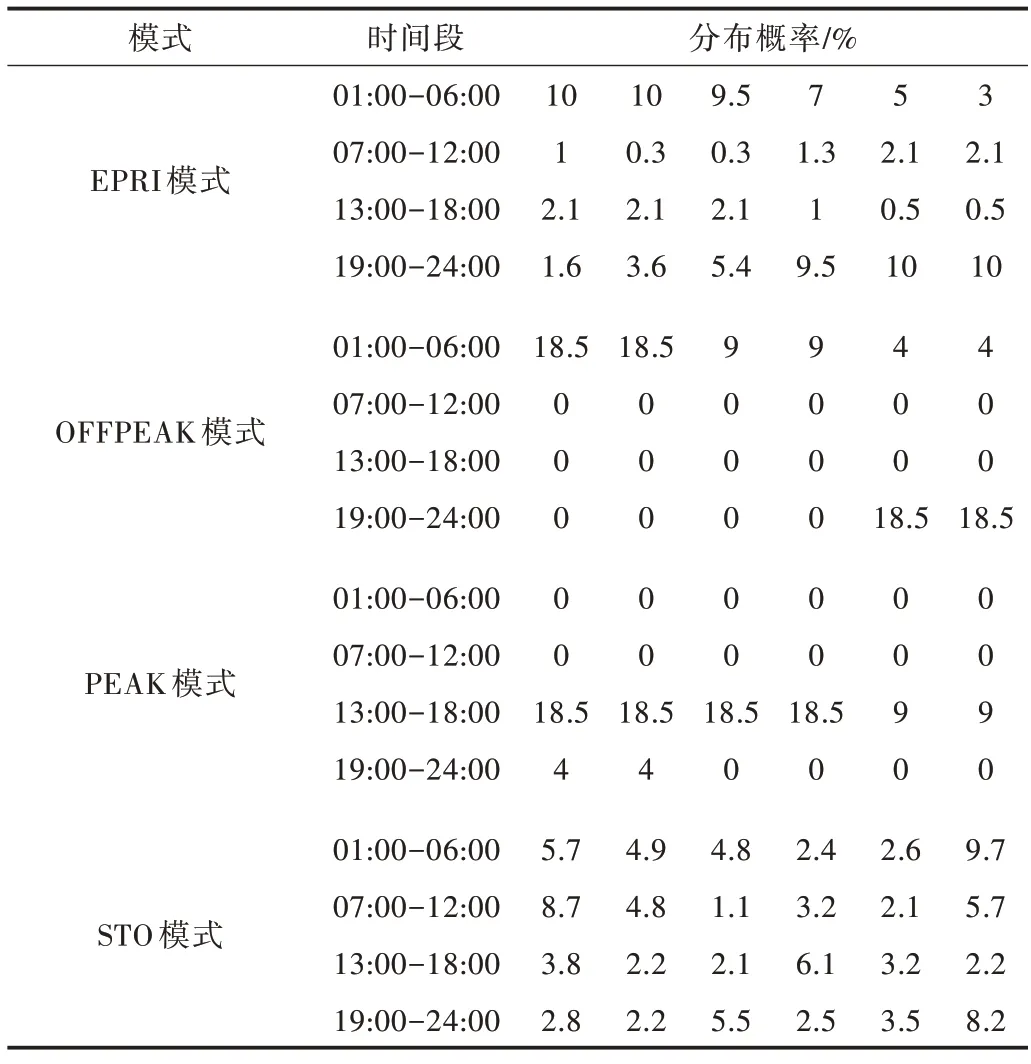
Table 1 Load distribution of four modes表1 4 种模式负载分布情况

在PSO 算法中，每个个体被视为D维搜索空间中的粒子，每个粒子具有位置矢量xi(t)=[xi1(t),xi2(t),…,xiD(t)]和速度矢量vi(t)=[vi1(t),vi2(t),…,viD(t)]。粒子根据以下方程更新其速度和位置：

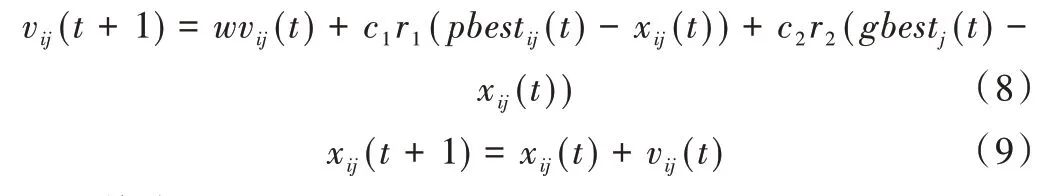
其中，pbesti(t)=[pbesti1(t),pbesti2(t),…,pbestiD(t)]是粒子i的个体最佳位置，gbest(t)=[gbest1(t),gbest2(t),…,gbestD(t)]是种群最佳位置，w为惯性权重，c1、c2是加速度系数，r1、r2是在［0，1］内均匀分布的两个随机实数。

2.2 BLPSO 算法

BLPSO 算法由文献［19］提出，其采用生物地理学粒子更新策略。在BLPSO 中，每个个体根据如下公式更新其速度和位置：

生物地理更新策略中最重要的部分是为每个个体生成学习样本，具体步骤如下：

首先，根据每个个体质量高低分配排名，即质量高的个体排名靠前，如下所示：

其次，根据个体排名为每个个体分配迁入率和迁出率。迁入率和迁出率计算公式如下：

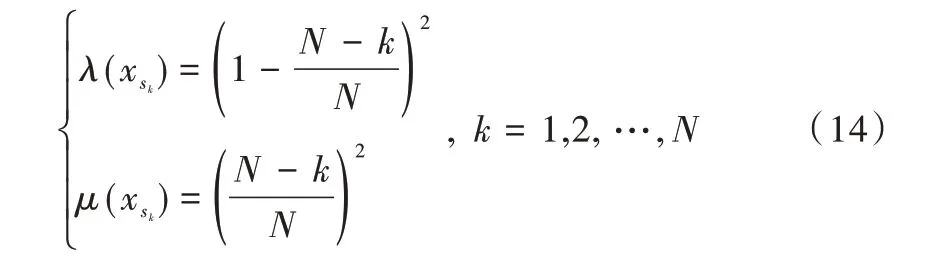
其中，λ()是迁入率，μ()是迁出率。

之后，采用生物地理学迁移算子为粒子i生成学习样本索引τi=[τi(1),τi(2),…,τi(D)]，具体如下：

2.3 BLPSO-OBS 算法

本文提出一种基于局部搜索的生物地理粒子群算法（BLPSO-OBS）以解决DED 问题，该算法在BLPSO 算法中引入了观察蜂局部搜索策略以进一步提高搜索精度。

2.3.1 OBS 局部搜索策略

观察蜂局部搜索策略（Onlooker Bee Search，OBS）是一种局部搜索策略，来自人工蜂群算法中的观察蜂搜索算子。OBS 实现步骤如下：

首先，根据每个个体适应度值为每个个体分配概率，即：

其中，f(xi)是个体i的适应度值，N是种群大小。

其次，每个个体根据如下公式更新其位置：

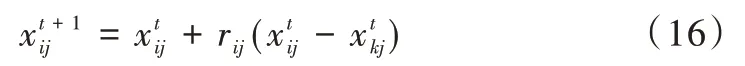
其中，k和j被随机选择，且满足k∈{1,2,…,N},j∈{1,2,…,D},k≠i；rij是在［-1，1］内均匀分布的随机实数。

OBS 局部搜索策略实现流程如下：

3 DED 问题解决

在使用BLPSO-OBS 解决DED 问题时，应考虑以下3 个重要问题：种群初始化、约束处理和终止条件。

3.1 种群初始化

在BLPSO-OBS 中，种群中的每个个体都是DED 问题的解决方案。如果每个调度时段有Ng个发电机组为负载供电，那么第i个个体的当前位置可由以下公式给出：

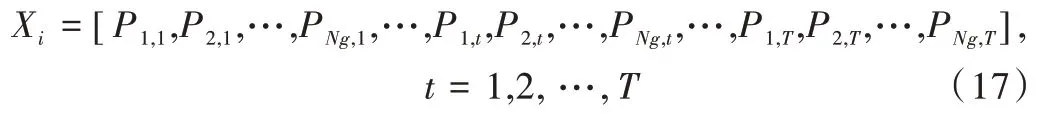
其中，T是DED 问题的调度时段数量，j是发电机组下标，Pj,t是第i个个体在第t个调度时段内第j个发电机组的输出功率。有T个调度时段、Ng个发电机组的DED 问题是一个T×Ng维度的问题。

3.2 约束处理

解决DED 问题最重要的是如何处理等式约束和不平等约束。DED 问题中有4 种约束类型：发电能力约束、爬坡约束、禁止操作区域约束和电力平衡约束。

对于发电能力约束和斜坡速率约束，可采用以下策略：

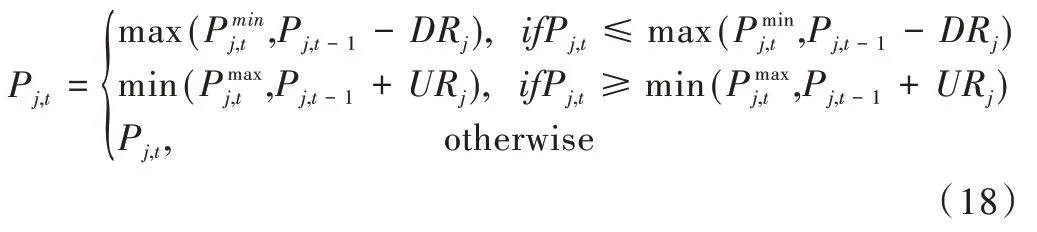
对于禁止操作区域约束，如果Pj,t位于第k个禁止操作区域，即，则将其截断到第k个禁止操作区域的最近边界，如下所示：

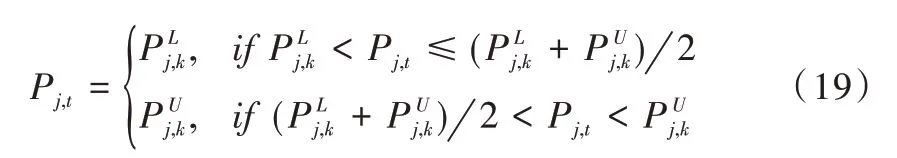
对于电力平衡约束，利用一种带有惩罚系数的修复算子进行修复。修复算子如下：

目标函数如下：

其中，K是惩罚系数,是等式约束的违反度。

3.3 终止条件

如果达到函数评估的最大次数max FES，则BLPSOOBS 算法将终止。

4 仿真结果与讨论

该测试系统由10 台发电机组成，可满足40 858MW 的负载需求，并包括爬坡约束和阀点效应。系统数据取自文献［10］、［17］、［20］，如表2 所示。

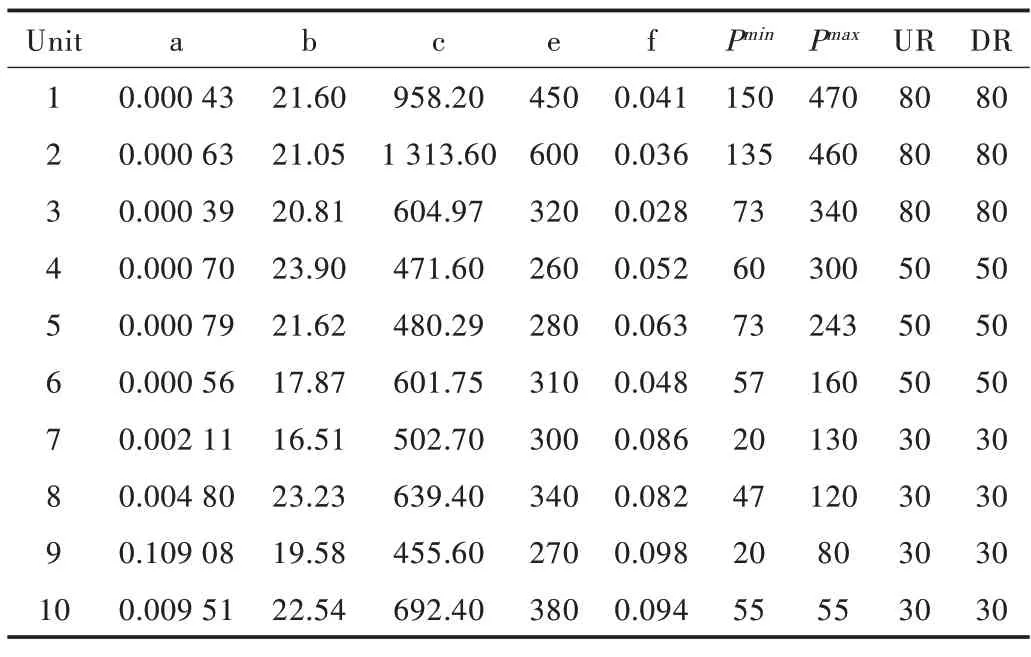
Table 2 Test system data（10 unit system）表2 测试系统数据（10 机组系统）

表3 中列出了BLPSO-OBS 与GQPSO、CLPSO、BBPSO、BLPSO［19］的统计结果比较。在这4 种模式中，BLPSO-OBS获得的最低、平均和最高燃料成本都是这些方法中最低的，标准差也最小。除EPRI 模式外，BLPSO-OBS 的计算时间也最短。

图1-图4 分别给出了所列算法在4 种模式下的收敛性比较，从中可以看出，BLPSO-OBS 的收敛速度最快。

5 结语

本文提出一种基于观察蜂局部搜索的生物地理粒子群算法（BLPSO-OBS），采用生物地理粒子更新策略与观察蜂局部搜索策略，用于求解含电动汽车的动态经济调度问题。BLPSO-OBS 算法被应用于具有电力平衡约束、爬坡约束与传输损耗约束的测试系统。实验结果表明，通过BLPSO-OBS 获得的燃料成本低于其它方法的燃料成本。将来计划对BLPSO-OBS 算法进行扩展，以解决其它更加复杂的经济调度问题，例如多燃料经济调度问题等。

Table 3 Comparison between fuel cost of test system and statistical results表3 测试系统燃料成本与统计结果比较

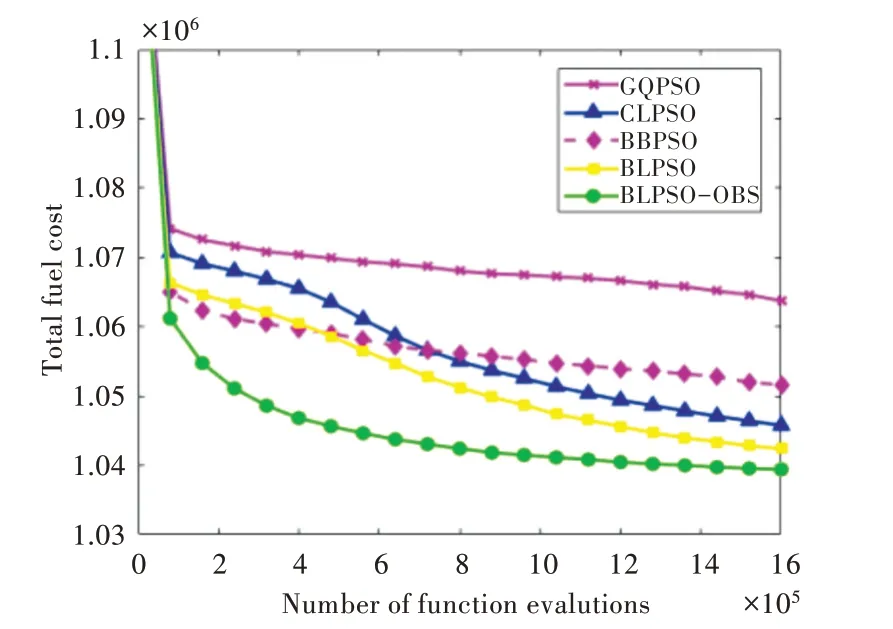
Fig.1 Convergence graph of EPRI mode图1 EPRI 模式收敛图

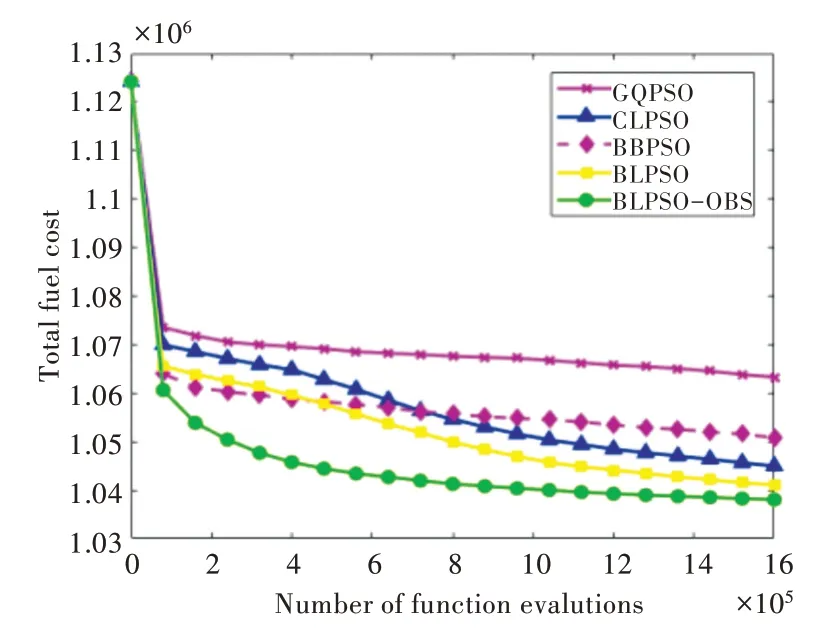
Fig.2 Convergence graph of OFFPEAK mode图2 OFFPEAK 模式收敛图

Fig.3 Convergence graph of PEAK mode图3 PEAK 模式收敛图

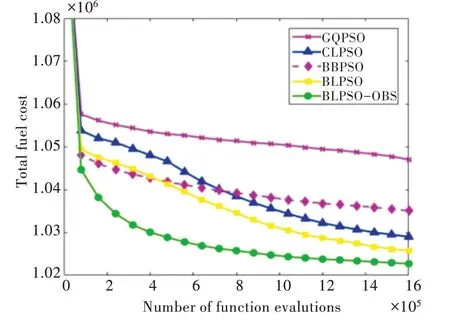
Fig.4 Convergence graph of STO mode图4 STO 模式收敛图