基于嵌入式多核系统的新型边界公平调度器设计
朱长昊,张凤登,杨甲丰
(上海理工大学光电信息与计算机工程学院,上海 200093)
0 引言
多核处理器经过十几年发展,逐渐成为市场主流,应用于多媒体计算、嵌入式设备、个人计算机等多个领域。基于多核系统的调度算法成为关键技术点,而调度算法有效性直接影响整个系统实时响应能力与资源使用率[1]。
Liu 等[2]建立了实时调度系统模型,并首次提出系统利用率相关概念;Baruah 等[3-4]分析了多处理器平台,提出公平调度(Boundary Fair,BF)的思想,在离散时间模型下,利用“特征字符串”标记任务优先级从而有效完成任务调度;Anderson 等[5]基于流体调度的思想简化公平调度的概念,改进公平调度算法使其调度开销更小,并在文献[6-7]中首次针对公平调度中的任务在每个时间单元作出决策需大量调度开销的问题,提出了早期释放的概念,以保证空闲处理器资源可有效利用;文献[8]对公平调度算法相关研究进行总结,并依次通过实验评估算法优缺点;Zhu 等[9]结合公平调度的概念,提出一种在任务调度截止时间边界位置进行调度决策的算法,有效解决了调度过程中任务切换与迁移造成的开销过大的问题;Nelissen 等[10]将BF 算法扩展到零星任务集的调度问题上;张慧娟等[11]归纳了多核系统中较成熟的调度算法,分析了目前解决调度开销过大问题的方法;吴星等[12]对BF 算法在多处理系统平台上的调度进行研究,实现了周期任务和非周期任务混合的任务实时调度;刘硕[13]总结了任务可调度性概念;梁浩等[14]基于实际过程中处理器系统不能有效解决实时的调度问题,提出一种新的可调度分析方法以增加实时任务集中可调度任务数量;邹圣雷[15]成功地将已有几种经典的调度算法移植到Linux 系统上以验证调度算法有效性。
本文基于现有BF 算法研究成果,依据流体调度思想简化BF 调度算法原理,并给出相关证明。在此基础上提出ER-BF 算法以解决任务中断阻塞时空闲处理器内核无法得到有效利用的问题,最后设计出新的边界公平调度器,通过实际任务参数对比验证新调度器有效性。
1 系统模型与可调度性分析
1.1 系统模型
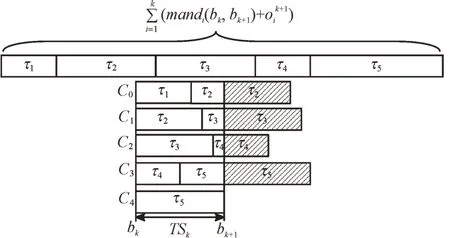
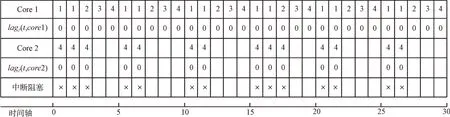
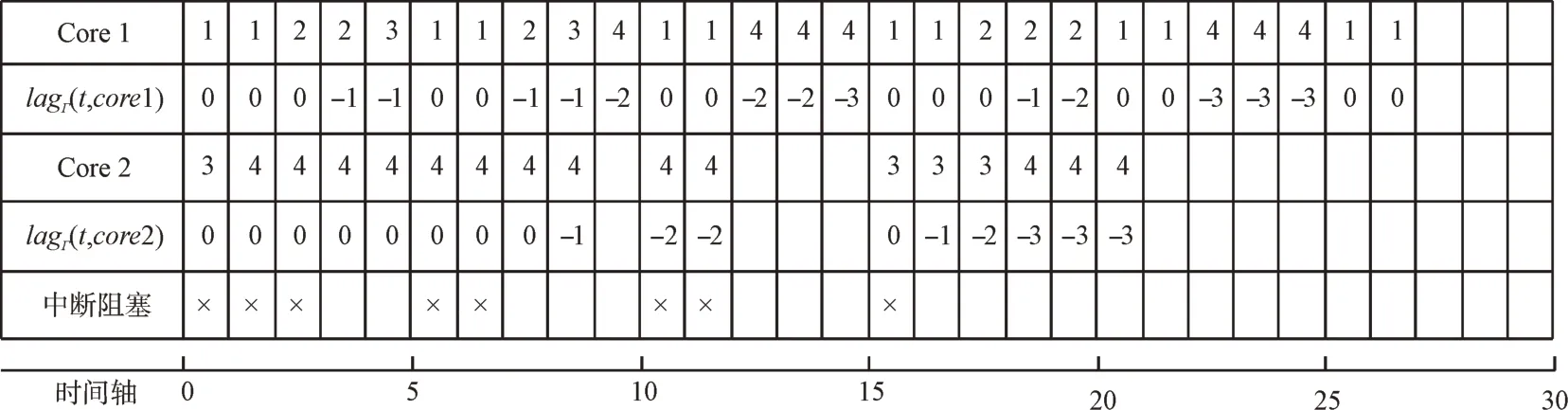
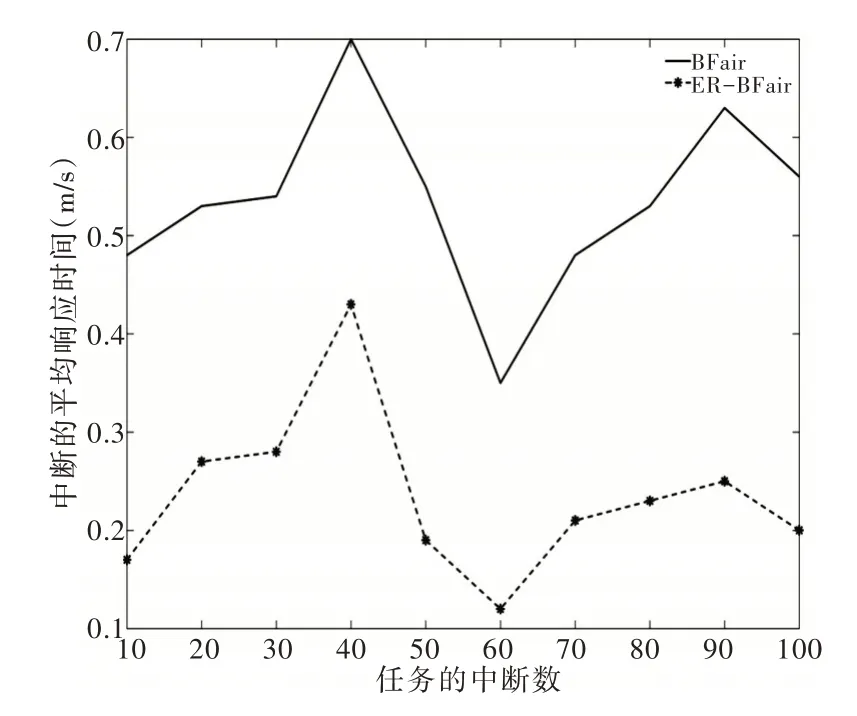
在m个具有相同处理能力的多核处理器系统平台上,调度1 个包含n个任务集的周期性实时任务,1 个周期任务集τ={τ1,τ2,…τn}由n个周期任务组成,每个任务τi={pi,di,ei}由其周期pi、截止时间di和最坏执行时间ei组成,任务执行时间ei不可以超过周期pi,即ei≤pi,且为系统时间单元整数倍。算法研究是基于任务,具有隐式截止期,即di=pi。任务τi利用率为wi且wi=ei/pi,wi≤1(i=1,2…n),若wi=1,该任务可直接分配1 个处理器内核执行。BF 算法以两个连续的任务截止期为边界,用bk表示调度边界[9],即调度器将在k时刻为下一时间片作出调度决策,k时刻对应的时间片表示为TSk,则TSk边界为bk和bk+1。用B={b0,b1,b2,b3,…}表示调度边界集合,其中b0=0,且bk 任务再被调度时有约束条件:①处理器内核不能同时共享同一个任务;②一个任务至多只能分配给一个处理器内核,即任务不容许并行[8];③该任务集的任务需相互独立,每个任务在执行期间不影响其他任务的释放时间。 在多核处理器系统调度问题中,1 个任务集若可被该系统调度,则该任务集中每个任务都要在其调度周期内满足其截止期要求,这也是1 个任务集可被调度的充分必要条件[16]。 定理1 在具有隐式截止期的任务集中,只有所有任务利用率总量不超过所有处理器总系统利用率,任务集才可被调度。即: 证明:将任务τi被分割成时间单元的无限序列,称为子任务[13](Subtask)。每个子任务都有一个时间单元的执行时间,任务τi的第j个子任务表示为τi,j且j≥1。每个子任务都有其释放时间r(τi),截止时间d(τi)和运行窗口|w(τi)|,显然对于子任务的释放应该是在前一个子任务执行完毕后才释放子任务,运行窗口应该处于释放时间与截止期之间。表达为: 由式(3)可以计算得出式(4)。 为了保证同一个任务多个子任务不在同一调度窗口重叠,且每个子任务均可满足在截止期前被调度,以一个子任务窗口为例,用U(τi,t)表示每个子任务在该窗口调度利用率分布情况,根据式(3)、式(4)可得: 根据式(5),在t=r(τi)时对于任意的正数x,都有≥x。由此可得: 在t=d(τi)-1 时,对于任意正数x,都有≥x,即-≤-x。由此可得: 综上,对于任意的时间单元t,都有U(τi,t) ≤wi,即当时,满足,则该任务集是可被调度的,原命题得证。 假设每个任务处理时间与任务利用率成比例,在离散时间系统中,任务总是执行系统单位时间整数倍,所以任务执行可能会偏离流体调度,为了测量流体调度偏差,引入任务分配误差(lag),相关定义如下: 定义1 设一种调度为流体调度(Fluid Schedule)[5],当且仅当对于任意时间t≥0,每个任务τi在时刻ai(t)释放其作业,已执行Ui× (t-ai(t))个时间单元。任务τi的lag是在流体调度中相同时刻t应执行工作量与在实际调度中直到时刻t执行的τi激活任务工作量之差,如式(8)所示。 其中ai(t)是τi的激活任务到达时间。 定义2 对于任务τi的调度可被称作边界公平[20],当且仅当在任何任务的执行边界处满足: 给定调度的分配误差为lagi(t),BF 调度要求任务在每个边界进行调度的分配误差总是小于系统时间单位,这主要因为系统是在离散的时间单元运行调度算法完成调度决策。 定理2 对于一个任务τi在时刻t,如果其实际执行时间比相应流体调度理论时间更短,即lagi(t) >0,表示该任务在时刻t滞后;如果实际执行时间比相应流体调度理论时间长,即lagi(t) <0,表示该任务在时刻t超前;如果其实际执行时间与相应流体调度时间相同,即lagi(t) <0,表示该任务在时刻t准时执行。 本文以1 个实际任务τi=(9,15,15)在处理器内核上进行调度的情况为例进行说明。该任务利用率为Ui=0.6 <1,满足前文证明的可调度性条件。如图1 所示,该任务在不同时刻执行时存在不同的调度可能性,在t=6 时刻系统分配的实际时间单元分别为3 和4 的情况下,任务出现的滞后与超前情况偏离了理想的流体调度(见图1(a)线)。为了保证任务在其截止期前完成调度,在该时刻之后,系统需分配更多时间单元给出现滞后调度(见图1(c)线)的情况,且应分配更少的执行时间单元给出现超前调度(见图1(b)线)的情况。但是无论中间如何分配执行时间单元,最后在时刻t=15 时,任务均需执行完毕。 Fig.1 Ideal fluid scheduling,lagging scheduling and advanced scheduling图1 任务理想流体调度、滞后调度与超前调度 综上所述,只有在所有任务利用率总量不超过所有处理器核总系统利用率,且在每个调度边界分配误差不超过1 时,才可认定该任务集可被BF 算法调度。 BF 调度算法为每个边界时间与下一个截止期边界之间的时间单元分配子任务执行,确定任务优先级时需考虑任务未来计算需求,保证任务在下一个时间点和未来任意边界点均不会错过截止期。所以对于有隐式截止期的周期性任务τi的下一边界bk+1应该为当前边界bk之后最早的截止时间,表达如式(10)所示。 为了确保每个边界公平性,每个任务τi必须分配一些整数的强制性单元,如果在为每个任务分配强制执行时间单元后,某些边界内还存在空闲的时间单元,则这些时间单元将动态地分配给符合条件的任务,BF 算法关键是要根据任务优先级分配这些可选单元。相关定义、定理及证明如下文所示。 定义3 BF 调度算法计算区间[bk,bk+1)内的最少执行时间,以满足下个边界区间内任务执行公平性,即lagi(bk+1)<1,这个最少的执行时间被称作强制执行时间单元(Mandatory Time Units)[9],分配给任务τi的强制执行时间定义为: 定义4 处理器核在边界区间[bk,bk+1)执行完任务的强制执行时间后,某个任务可能存在没有被执行的部分,这些未被执行的部分被称作挂起的工作(Pending Task)[9],记为PWik。一个任务被挂起的工作表示其在该边界时刻分配误差与执行时间和强制执行时间的差值,如式(12)所示。 任务在时间区间的执行时间为(bk+1-bk)·wi,被挂起的工作是该任务完成其强制执行时间后的小数部分,所以lagi(bk+1)=PWik+1-oik+1。 定理3 设任务已经分配完成强制执行时间,任务τi在下一个边界时刻bk+1的分配误差需要满足lagi(bk)<1 以保证任务在边界时刻的公平性,若在这个边界区间内已经执行分配的强制时间,剩下未分配时间称作可选分配时间(Remaining Time Unit),记为RU(bk,bk+1)。 证明:边界区间[bk,bk+1)中,对于m个处理器内核来说,可用来分配的执行时间为m·(bk+1-bk),但是每个任务均需有强制的执行时间,这些任务在边界区间[bk,bk+1)强制执行时间结束后,m个处理器内核剩余下来的分配时间是可选分配时间的值。 可选分配时间应分配给任务,则每个任务都需竞争使用RU(bk,bk+1)个时间单元,以实现任务在截止期前完成调度,但是每个任务最多可竞争接收1 个时间单元的可选分配时间。任务τi在[bk,bk+1]的时间单元内若被分配1 个可选分配时间,记为oik+1=1,否则oi k+1=0。定理4 如果任务利用率之和小于等于处理器内核个数,在所有边界集合B={b0,b1,b2,b3,…bn-1}内,=0且lagin-1<1,对于所有处理器内核和在边界内的总处理时间来说,满足式(14)。 证明:通过反证法进行证明。在以上条件下,若假设原命题不成立,即(bk+1-bk)·m<,对于每个边界处满足总的分配误差为0 且总系统利用率为m,则根据定义4,有以下等式成立: 显然对于任意一个任务集,确定好强制执行时间后,其未被执行的部分不少于0,即,与假设相矛盾。所以假设不成立,原命题成立。 每个任务在每个边界内的执行都有其优先级,根据定义1,如果1 个正在执行的任务τi在边界时刻t被打断执行,则发现这个任务分配误差将逐渐增大,显然它的值与任务利用率Ui成比例关系,当任务τi有x个时间单元未被执行,其分配误差会变为: 根据定义2,任务分配误差需满足在任意一个边界时刻t有lagi(t) <1,所以用最小的时间单位x表示任务τi的紧急因子(Urgency Factory),记为UFi(t)。如果τi从当前时刻t到时刻t+x没有执行,则lagi(t+x)将超过1,这个量可通过式(17)求解。 定义5 任务τi在时刻t的紧急因子为UFi(t),如果τi从时刻t到时刻t+x没有执行,则其在时刻t+UFi(t)的分配误差lagi(t+UFi(t))大于等于1,如式(18)所示。 假设在时刻t,停止执行任务τi,并在最后一个时间单元恢复任务执行,即不在t到t+UFi(t) -1 时间内执行任务τi,则根据定义1,任务在时刻t+UFi(t) -1 的分配误差为: 为了保证τi赶上时刻t的流体调度偏差,需执行y个时间单元的任务,如式(20)所示。 其中,y值可被定义为在t时刻,τi恢复到分配误差变为0 需要的时间单元,被称为恢复时间(Recovery Time),记为ρi(t),则可给出恢复时间的定义。 定义6 任务τi在时刻t上的恢复时间ρi(t)是任务τi准时完成执行所需要的最小执行时间,如式(21)所示。 根据定义5 与定义6,对于两个任务τi与τj,在时刻t任务τi优先级高于τj,记作τi≻τj,约束条件为:UFi(t) 任务紧急因子越小说明任务如果再不执行,其分配误差将会大于1,即任务优先级越高。而任务恢复时间越大,说明τi需要比τj用更多的执行时间弥补其在流体调度过程的延迟,但更长的时耗也限制了未来调度决策。若两个任务紧急因子与恢复时间相同,即两个任务优先级相同,则可由调度器决定哪个任务优先调度。 在BF 算法中,为了使所有任务在其截止期前完成,在确定强制执行时间后,由两个条件判断哪些任务可优先获得可选执行时间。 条件1 根据定理4可知manki(bk+1-bk)<(bk+1-bk),这样可避免因1 个处理器核在边界时间片[bk,bk+1)由于可分配给任务的时间单元不够,导致任务进入下个处理器核执行,即任务在多个处理器核上并发执行的问题, 条件2 更高优先级的任务有资格获得可选的执行时间单元。 这保证了在每个边界的公平性。通过概念分析发现,BF 算法要求在每个边界处分配误差为0。如果去掉分配误差必须大于1 的约束条件,即容许任务超前完成,以保证有效利用处于空闲状态的处理器内核,称之为连续型调度策略,更改可调度性约束后的算法称为ER-BF 调度算法。 由于任务可提前释放执行,ER-BF 算法给每个任务分配可选时间单元的数量没有限制。同时为了让处理器内核有效处理任务的中断,提高调度效率,若Ui>m/2,表示系统为重载系统,相对应的为轻载系统。对于重载系统,ER-BF 算法需考虑将中断任务分配到空闲的内核上执行,以此取代BF 算法使用的固定内核执行中断,这样可有效减少任务中断过程中的阻塞问题。 (1)应该树立科学的质量管理理念,整个建筑工程中的全部施工者都应该对自己应尽的责任和义务以及施工合同中的内容有一个清晰的了解,并且在施工的过程中,严格按照施工合同中的规定完成自己的工作。同时建立完备的施工安全和质量管理方案,在加强对建筑工程施工质量控制的前提下,通过实行有效的措施,杜绝施工过程中会发生的种种问题,从而确保建筑工程的施工质量。 根据McNaughton[17]提出的环绕算法,将执行时间分配到各个内核上并生成静态调度表,规则描述如下: (1)分配给每个处理器核的执行时间不容许超过该边界时间长度TSk。即: (2)分配给总处理器内核的执行时间不超过处理器内核在该边界的可用来处理任务的总时间。即: 假设有可被BF 算法调度的任务集τ={τ1,τ2,τ3,τ4,τ5},如图2 所示,可以表示1 个边界内任务在5 个内核上的执行情况。 Fig.2 Task set allocation图2 任务集分配情况 图2 中阴影部分指当前任务在该处理器内核上未执行完迁移到下1 个处理器内核上执行的部分。 基于ER-BF 算法原理,设计新型边界公平调度器程序流程,如图3 所示。 Fig.3 ER-BF scheduler program flow图3 ER-BF 调度器程序流程 步骤1 输入任务集并计算任务集每个任务利用率,对任务集进行可调度性分析,若任务集可使用ER-BF 调度算法进行调度,则可根据每个任务周期确定每个周期性任务的任务调度边界bk,同时要确保bk小于该任务集所有任务周期最小公倍数(LCM)。 步骤2 计算任务在每个边界处的分配误差,即每个任务在其边界处调度的分配误差lagi(bk)<1,如果所有任务在其边界处分配误差小于1,则可证明任务在边界前执行具有公平性。之后根据定义3 计算任务在某个边界区间[bk,bk+1)内强制执行时间manki(bk,bk+1),根据定理3 计算任务可选分配时间RU(bk,bk+1),同时根据定义4 计算被挂起的工作PWi。 步骤3 通过定义5、定义6 计算两个任务的紧急因子UFi(t)和恢复时间ρi(t),并比较任务优先级。 步骤4 根据条件1 与条件2 确定哪些任务可获得可选执行时间,按照每个任务在每个边界内的优先级与执行的时间单元生成任务调度表。 本文基于Litmus-RT 平台对ER-BF 调度器进行设计[18]。Litmus-RT 平台是基于Linux 系统为实时系统研究提供内核级别抽象的接口实验平台,可用于实时可调度性测试、任务集生成和实验数据采集。实验平台搭建后,导入实验任务参数,生成任务集,最后分配任务生成调度表,对比ER-BF 调度器与BF 调度器执行效率。ER-BF 调度器伪代码为: 完成两种调度器设计后,输入任务集Γ={τ1,τ2,τ3,τ4},其中每个任务参数为τ1=(2,5,5)、τ2=(3,15,15)、τ3=(3,15,15)和τ4=(20,30,30),任务ID 为{1,2,3,4},将任务集Γ执行于两个内核上。计算可得知UΓ=1.47 <2,满足可调度性条件,且该系统为重载系统。任务集Γ通过BF 调度器执行生成的调度表,如图4 所示,通过ER-BF 调度器执行生成的调度表,如图5 所示。 Fig.4 Schedule generated by BF scheduler for task set Γ图4 任务集Γ 通过BF 调度器生成的调度 Fig.5 Schedule generated by ER-BF scheduler for task set Γ图5 任务集Γ 通过ER-BF 调度器生成的调度 基于同1 个任务集,从图4 可看出,使用BF 调度器,最坏的情况是每5 个时间单元就有3 个被阻塞。从图5 看出,通过增加连续工作机制,不仅可缩短任务完成时间,而且中断阻塞时间点较图4 明显减少,由于中断即可将任务传递至空闲的处理器内核,缩短了中断响应时间[19]。由此可知BF 调度器是按一定进度执行任务,这使任务的lag在限定的(-1,1)之间,而ER-BF 调度器允许任务超前执行,在lagi(t) <0 的条件下,有更多时间裕度留给中断响应以便进一步处理,可缩短中断响应时间。 针对任务集Γ,用两种调度器依次执行几个任务周期,观察随着任务中断的增多,中断平均响应时间情况。由图6 可知随着任务中断数增多,相比于BF 调度器,任务通过ER-BF 调度器调度的总平均中断响应时间缩短56%以上。 Fig.6 Average response time of task set interruption under two schedulers图6 两种调度器下任务集中断的平均响应时间 本文首先基于多核系统,通过流体调度思想分析BF 调度算法原理,给出相关定义并证明其定理,分析简化该算法后提出任务优先级对比规则,以支持任务集满足其截止时间;由此去掉任务不可超前执行的约束条件,即分配误差可容许小于-1,改进BF 调度算法后提出ER-BF 调度算法;最后基于ER-BF 算法设计调度器,将同1 个任务集通过这两种调度器进行调度,生成调度表。实验结果表明,ER-BF 可有效减少任务中断阻塞概率,且任务平均中断响应时间减少超过56%,大幅降低了系统开销。但本文仅基于虚拟的多核系统条件下进行验证,并没有实际运用于多核处理器任务调度,调度器实际性能有待进一步检验。
1.2 可调度性分析

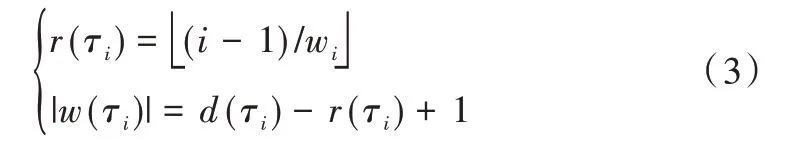
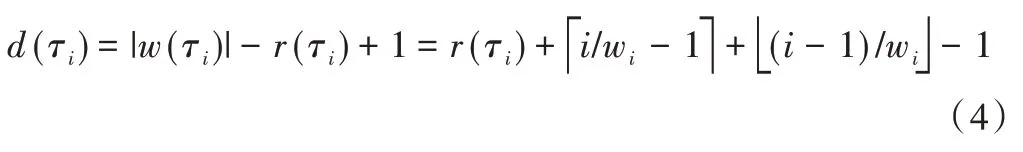

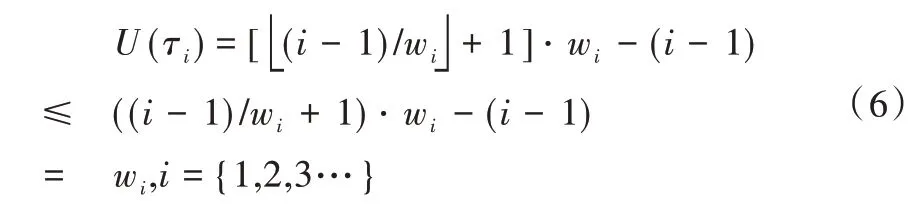




2 边界公平调度算法
2.1 基础定义与定理


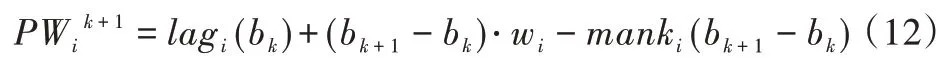

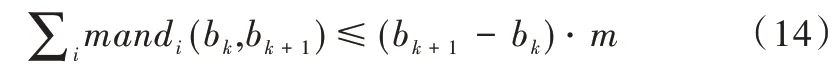

2.2 任务优先级判定
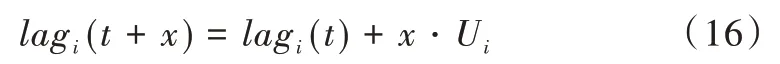

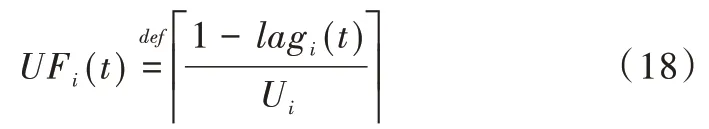

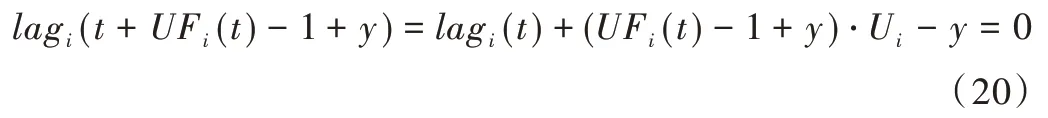

2.3 改进边界公平调度算法原理

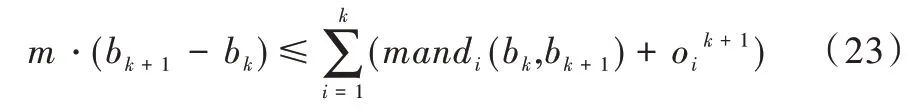
3 ER-BF 调度器设计与仿真对比
3.1 ER-BF 调度器设计流程

3.2 实验仿真设计


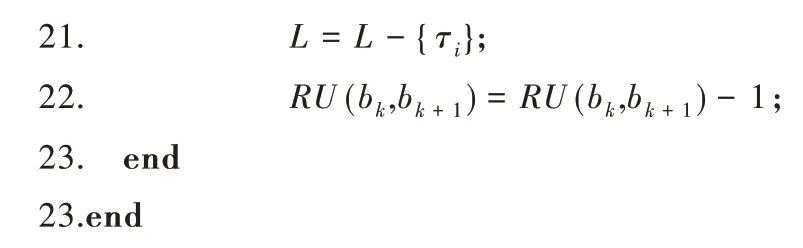
3.3 两种调度器对比评估
4 结语

