运营多年的刚架拱桥加固效果评价

钟辉武

（1.广东盛翔交通工程检测有限公司，广东广州511400；2.广东和立土木工程有限公司，广东广州511400）

0 引言

刚架拱桥具有杆件少、自重轻、施工简便、材料省、造价低、造型美观等优点，现役桥梁中仍大量存在，不过刚架拱桥由于整体性较差，容易出现结构开裂、损伤等病害，大部分刚架拱桥需进行维修或加固。但是随着社会经济的发展及交通流量增长，该类型的桥梁在加固运营多年后，其承载能力是否下降，能否满足原加固设计荷载标准的要求，需要进行评估[1]。以某钢筋混凝土刚架拱桥为研究对象，通过荷载试验评定该桥，在加固且运营多年后的承载能力是否满足原加固设计荷载标准要求，同时评价加固效果是否良好[2]。

1 工程概况

博罗大桥位于罗阳镇，跨越东江，1999年建成。桥梁全长1083.26m，引桥桥面全宽为23m，主桥桥面全宽25.4m。该桥上部结构桥跨组合为16m+2×45m+2×80m+16×45m+6m，其中主桥上部结构为钢筋混凝土等截面中承式吊杆拱；引桥上部结构为单跨跨径45m（墩中距47.5m），矢跨比为1/8 的变截面实心矩形钢筋混凝土刚架拱、16m 跨径的钢筋混凝土简支T 梁和6m 跨径的钢筋混凝土简支肋梁。主桥桥墩采用钢筋混凝土空心墩、沉井基础，其余墩采用钻孔灌注桩基础。桥梁设计荷载等级为：汽车-20 级，挂车-100，人群3.5kN/m2。该桥于2010年对6～9#跨主拱肋、弦杆采用10mm 厚度的钢板加固，横系梁采用8mm 厚度的钢板加固，主拱脚、斜腿采用增大截面外包15cm 厚的钢筋混凝土加固。

2 静载试验

2.1 测试桥跨与控制截面

为评定刚架拱桥的承载能力，根据《公路桥梁承载能力检测评定规程》（JTG/T J21—2011）并结合现场条件，选取该桥6#跨作为试验桥跨，应力控制截面设4 个（A、B、C、D 截面，），挠度控制截面设1 个（A截面）。测试控制截面如图1所示，截面应变测点布置图如图2～5所示。

图1 测试控制截面（单位：cm）

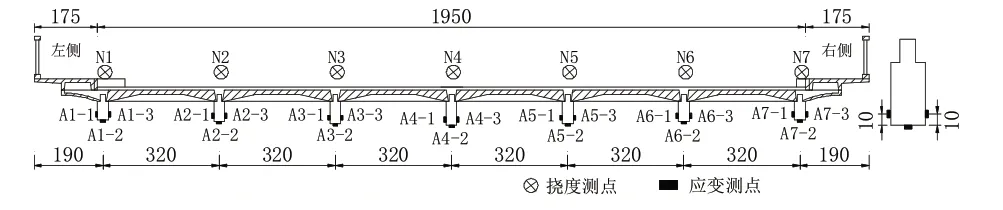
图2 A 截面挠度、应变测点布置图（单位：cm）

图3 B 截面应变测点布置图（单位：cm）

图4 C 截面应变测点布置图（单位：cm）

图5 D 截面应变测点布置图（单位：cm）

2.2 静载试验工况及加载效率

根据该桥竣工及加固设计图纸，本次荷载试验以汽车-20 级，挂车-100 作为桥梁控制荷载，其中汽车荷载按规范计入冲击效应。采用MIDAS/Civil 通用有限元软件建立刚架拱桥全桥空间有限元模型（连拱空间有限元模型，见图6），并考虑连拱效应，模型共划分为9116 个节点和9687 个空间梁单元及1776 个板单元，采用该模型进行设计荷载及试验荷载内力、试验荷载反应和自振特性的分析计算[3]。根据《公路桥梁承载能力检测评定规程》（JTG/T J21—2011）规定：静力荷载试验效率宜介于0.95～1.05 之间。静载试验荷载效率如表1所示。车辆布载示意图如图7～10所示。

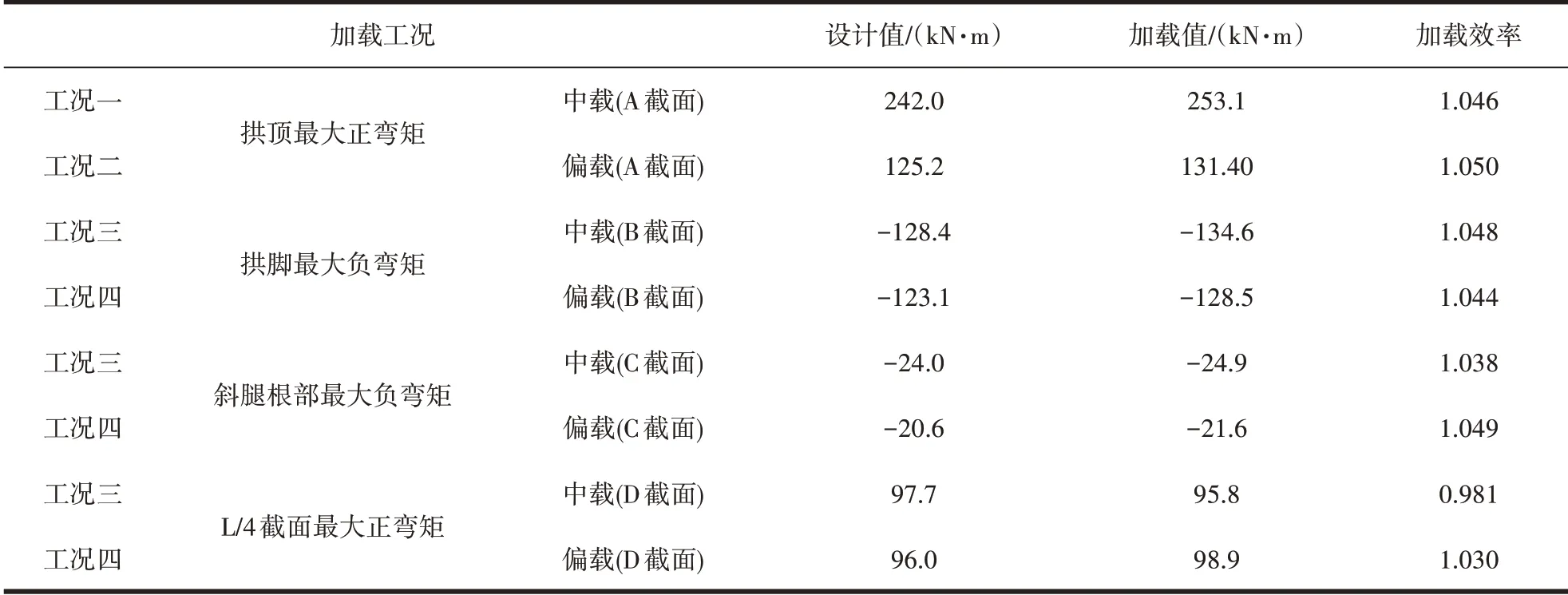
表1 静载试验荷载效率

图6 连拱空间有限元模型

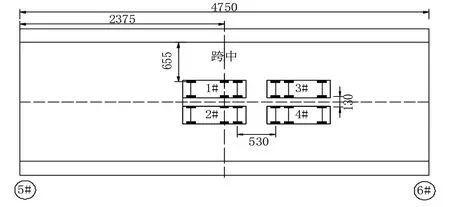
图7 工况一车辆布载示意图（单位：cm）

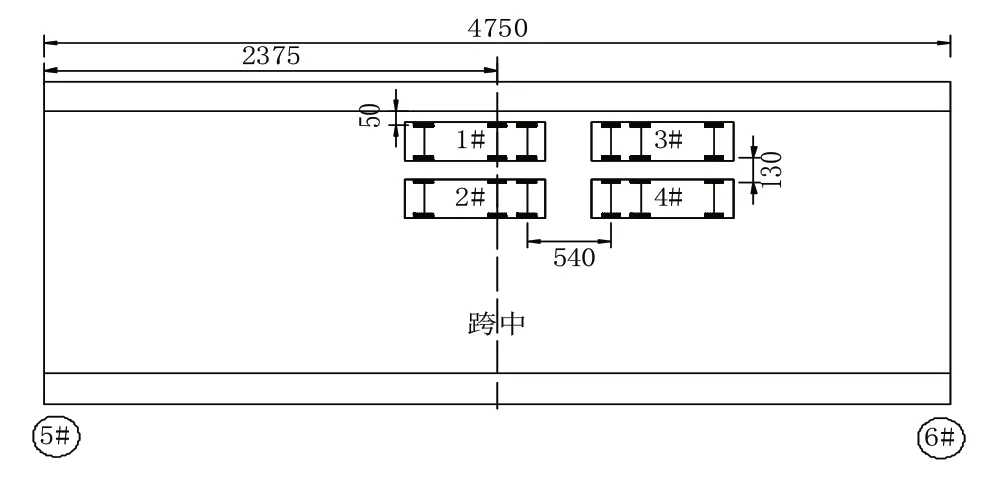
图8 工况二车辆布载示意图（单位：cm）

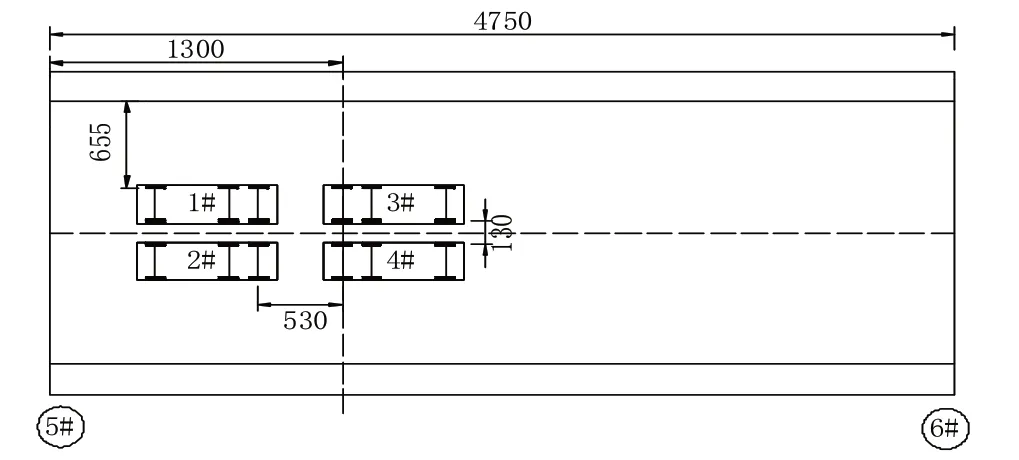
图9 工况三车辆布载示意图（单位：cm）

图10 工况四车辆布载示意图（单位：cm）

2.3 静载试验结果分析

各控制截面在试验工况下，主要控制测点实测应变值均小于理论计算值，主要控制测点的应变校验系数范围为0.06～0.98，卸载后相对残余变形均小于20%，测试结果规律正常，表明所测桥跨强度满足设计要求；拱顶截面在试验工况下，测点实测挠度均小于理论计算值，各挠度测点的校验系数为0.59～0.96，所测桥跨刚度满足设计要求。卸载后相对残余变形均小于20%，表明结构处于弹性工作状态，实测数据与理论值对比分析，见图11～20所示。

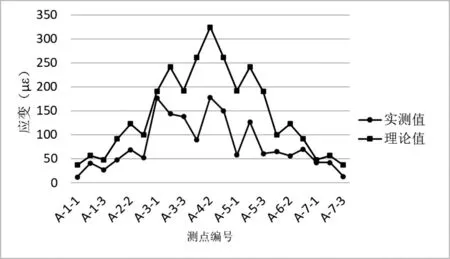
图11 工况一拱顶A 截面应变测点（中载）弹性应变值与计算值对比图

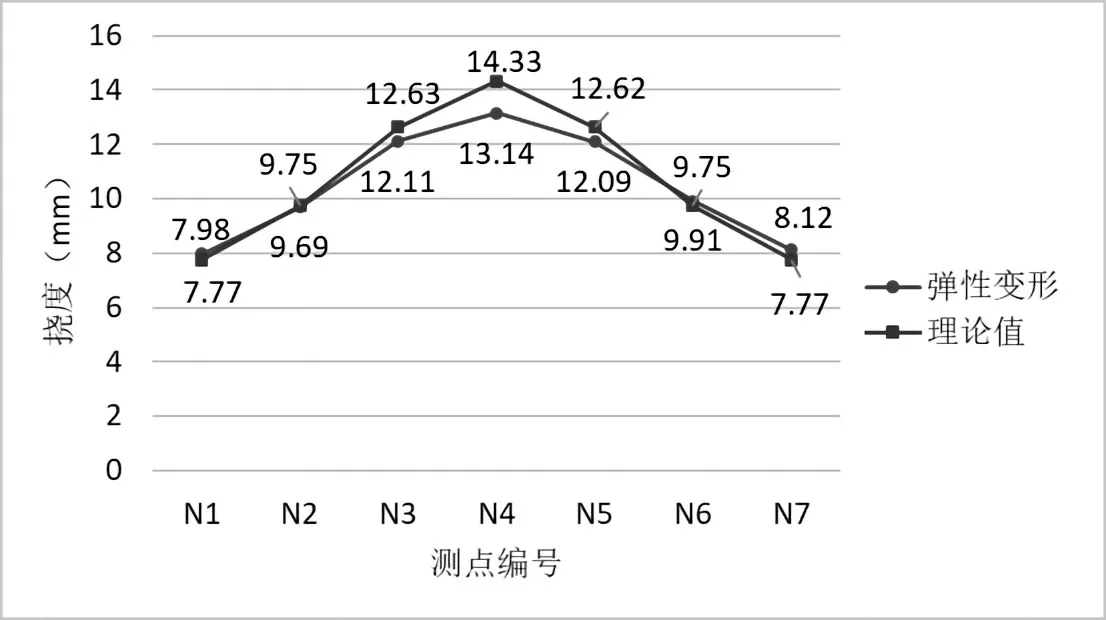
图12 工况一拱顶A 截面（中载）挠度实测值与理论值对比图

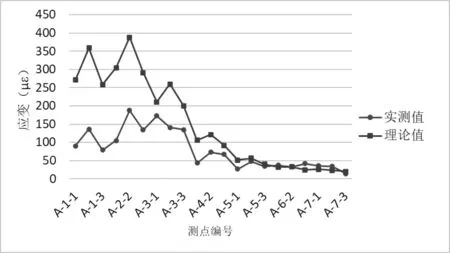
图13 工况二拱顶A 截面应变测点（偏载）弹性应变值与计算值对比图

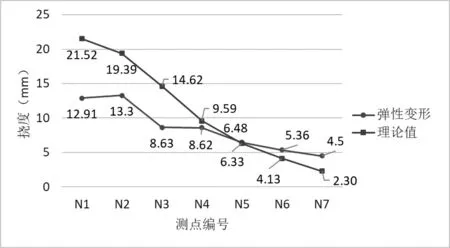
图14 工况二拱顶A 截面（偏载）挠度实测值与理论值对比图

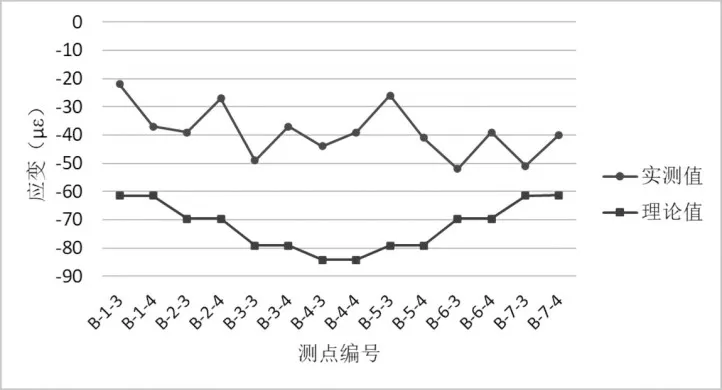
图15 工况三拱脚最大负弯矩B 截面应变测点（中载）弹性应变值与计算值对比图

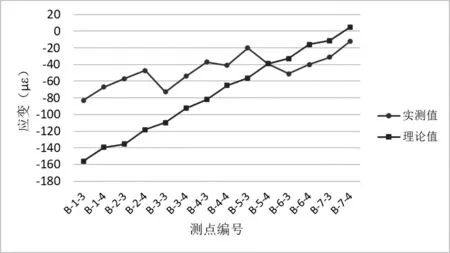
图16 工况四拱脚最大负弯矩B 截面应变测点（偏载）弹性应变值与计算值对比图

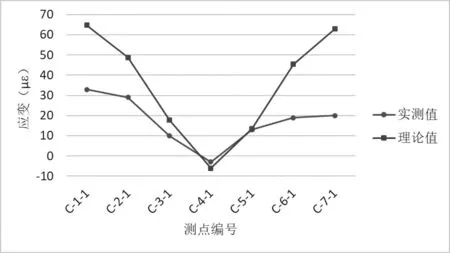
图17 工况三斜腿根部最大负弯矩C 截面应变测点（中载）弹性应变值与计算值对比图

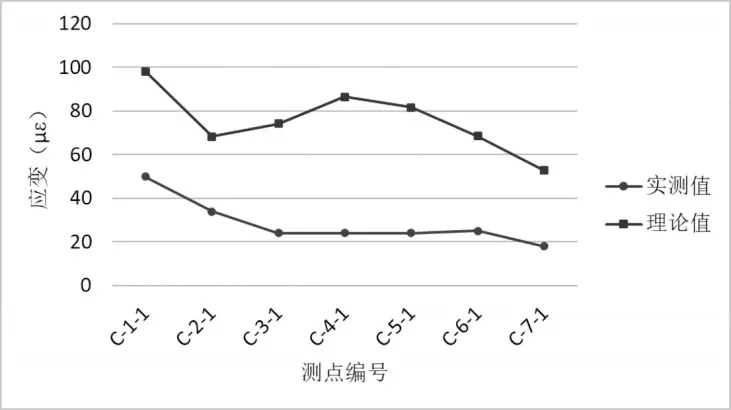
图18 工况四斜腿根部最大负弯矩C 截面应变测点（偏载）弹性应变值与计算值对比图

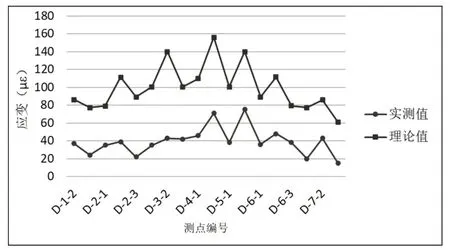
图19 工况三L/4 截面最大正弯矩D 截面应变测点（中载）弹性应变值与计算值对比图

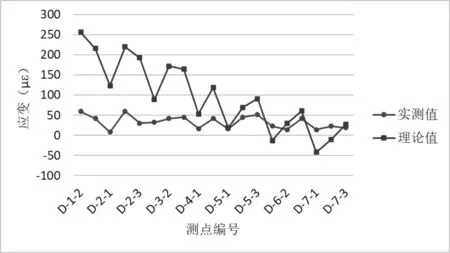
图20 工况四L/4 截面最大正弯矩D 截面应变测点（偏载）弹性应变值与计算值对比图

3 动载试验

3.1 试验测点布置及试验工况

环境随机激振法试验：测试点布置在6#跨1/4L、2/4L、3/4L 的桥面；无障碍行车试验：测试截面布置在6#跨跨中截面，在4#拱肋布置2 个动应变测点，试验工况采用4 种车速（20～50km/h）跑车进行动力响应测试。

3.2 试验结果分析

3.2.1 自振频率测试

采用低频高灵敏振动传感器测定主拱圈自振及脉动信号，通过频谱分析得到拱肋结构的竖向自振频率，阻尼比根据自振信号的衰减特性计算得到。实测6#跨竖向一阶频率2.148Hz 略大于理论计算频率2.002Hz，表明结构实际刚度大于理论计算刚度，与静载试验挠度检测结果相符，自振频率测试结果如表2所示。

表2 自振频率测试结果

3.2.2 冲击系数计算

桥梁冲击系数采用动应变和动挠度的时程曲线计算。结合现场条件，采用动应变时程曲线计算桥梁冲击系数，实测20～50km/h 跑车试验下，6#跨4#肋的冲击系数，分别为0.041～0.103，并与车速有十分明显的相关性，在时速（20～40km/h）冲击系数大于规范计算值（0.10），50km/h 的冲击系数基本与规范计算值相符合[4]，跑车试验实测冲击系数，如表3所示；冲击系数随车速变化曲线，见图21。

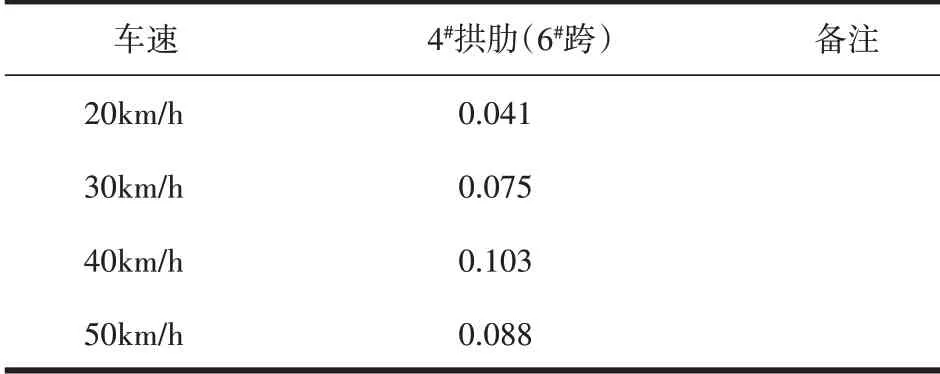
表3 跑车试验实测冲击系数

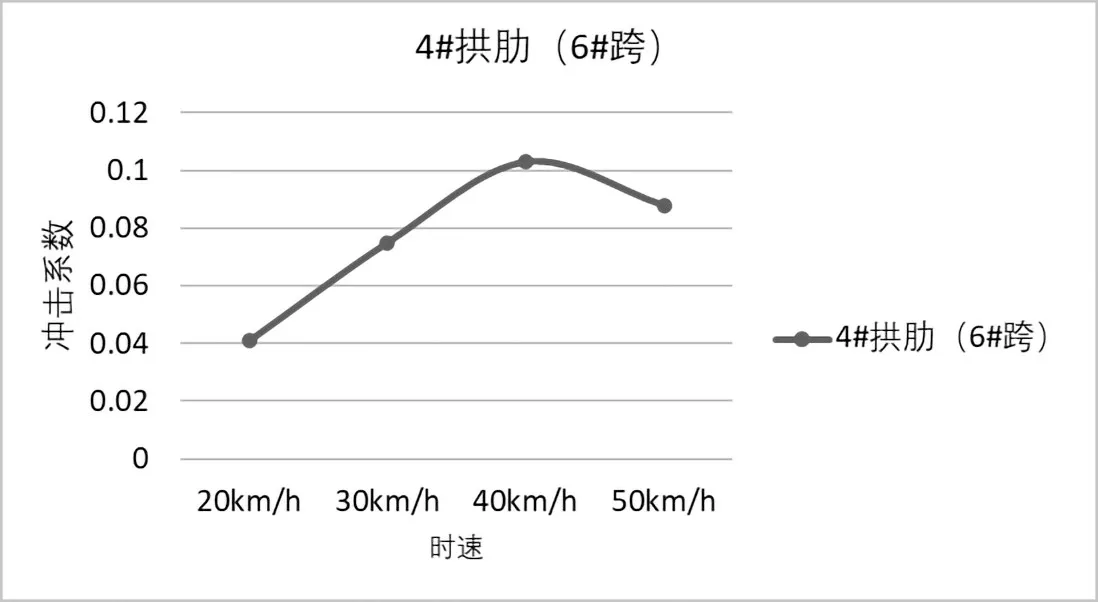
图21 冲击系数随车速变化曲线

4 结论

一是静载试验控制截面在试验工况下主要控制测点实测应变值均小于理论计算值，主要控制测点的应变校验系数、卸载后相对残余变形均满足规范要求，表明所测桥跨强度满足设计要求；

二是拱顶截面在试验工况下主要测点实测挠度均小于理论计算值，各挠度测点的校验系数、卸载后相对残余变形均满足规范要求，表明所测桥跨刚度满足设计要求；

三是竖向一阶频率2.148Hz 略大于理论计算频率2.002Hz，表明结构实际刚度大于理论计算刚度，与静载试验挠度检测结果相符。

分析结果表明：经加固运营多年后的某刚架拱桥承载能力满足原加固设计荷载标准，原采取的拱脚、斜腿增大截面、拱肋粘贴钢板加固效果良好。