100 m高钢筋混凝土烟囱双向切口爆破时差研究*

高文乐，刘志成，李坤鹏，史卓金

(1.山东科技大学 土木工程与建筑学院，青岛 266590;2.中铁十四局建筑分公司，济南 250014)

随着国家对环境保护的重视，一些高污染、高耗能的火力发电被关停或者进行升级改造，许多废弃的高耸烟囱等构筑物需要拆除。往往受场地大小的限制，单向低位爆破切口的爆破形式已经不能满足倒塌周围空间的要求，因此折叠爆破拆除的形式应用越来越多。为了确保烟囱爆破拆除的经济和安全，许多学者通过数值模拟对烟囱的爆破拆除的过程进行了计算。其中薛江波对砖烟囱破坏分析之后，通过分离式建模进行数值模拟的方式对钢筋混凝土烟囱单向倒塌爆破拆除进行计算，数值模拟得出的数据与在爆破现场测到的数据高度一致[1]。Munjiza和Friedhelm采集烟囱爆破过程中爆堆范围以及烟囱整体触地速度的数据，与数值模拟进行对比分析，试验证明数值模拟的模型和前处理数据可以用到工程实际中[2,3]。武哲分析了处于复杂环境中的一栋90 m高框架剪力墙结构楼房采用三个爆破切口进行爆破拆除的技术，最终得到了理想的爆破效果[4]。任江通过对烟囱的结构分析，考虑烟道和灰斗板对烟囱倒塌的不利影响，通过封堵现有烟道，应用复式梯形的切口形式，开设定向窗和导向窗对爆破方向精准定位等，最终实现了烟囱按照预定方向倒塌[5]。叶家明通过应力条件计算出水塔爆破缺口的圆心角大小和刚度条件计算出水塔爆破缺口高度，并基于ANSYS/LS-DYNA软件，对水塔的定向倒塌进行数值模拟，数值模拟分析也验证了水塔不能倒塌的结果[6]。采用基于LS-DYNA联合Hypermesh的方法对寿光巨能热电厂100m高的烟囱进行了数值模拟，并进一步利用数值模拟的方法对上下爆破切口的最佳起爆时差进行研究，对相似工程爆破设计和施工具有较大参考价值。

1 工程概述

寿光市侯镇南部巨能热电厂，是一座废弃电厂，内部发电设备已经拆除。其院内有一高为100 m的钢筋混凝土烟囱需进行爆破拆除。周围环境为：烟囱东距3层厂房50 m，南距鲁丽热电厂120 m、本厂平房80 m，西、北距最近厂房70 m。如图1。

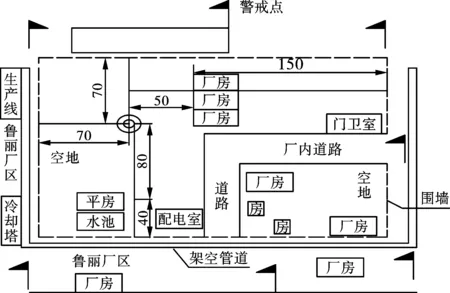
图 1 爆破周围环境示意图(单位：m)Fig. 1 Surrounding environment of blasting(unit:m)

烟囱顶部排烟口直径3.5 m，壁厚160 mm，烟囱底部外直径8.3 m、壁厚360 mm。混凝土烟囱内部设置有耐火砖内衬和隔热层，其中隔热层厚50 mm，内衬在5 m以下的厚度为230 mm，5 m以上为120 mm；竖向配筋为0～15 m为φ22、15～50 m为φ20、50～80 m为φ16，底部为双层钢筋网片结构，上部为单层钢筋网片结构。烟囱底部基座为直径15 m，深1.8 m钢筋混凝土结构[7]。

2 爆破方案及爆破参数

2.1 爆破拆除方案的选择

烟囱的爆破拆除主要有定向倒塌、原地坍塌和折叠倒塌三种方式，折叠倒塌又分为异向和同向折叠倒塌[8]。待拆烟囱在烟囱向下的冲击力不够的情况下，原地坍塌方案很难对烟囱的倒塌方向进行控制；同时，周围距离明显无法满足高度100 m烟囱的定向倒塌爆破；根据待拆烟囱的周围环境以及对烟囱结构的分析，选择折叠倒塌爆破方案。由于作业场地大小的限制，爆破拆除时不仅在烟囱底部设置爆破切口，还要在其中部的适当位置炸开一个或一个以上的切口，使烟囱朝向两个或两个以上的方向进行同向或反向分段折叠倒塌。在正南正北方向上距离最近建筑物的距离大于70 m，满足倒塌范围需求，有足够的安全距离，故选用双向折叠倒塌爆破拆除[9]。即充分利用中间平台，分+0～+50 m和50～100 m两段，分别设计上下两个爆破切口，上部向正北、下部向正南方向倒塌的双向折叠倒塌。

2.2 爆破切口参数

(1)切口位置

根据充分的研究和分析得出，烟囱的下部爆破切口设置为0.5 m以上，此位置外径为8.3 m、壁厚0.36 m，重量为1200.98 t，重心高度为23.6 m。上部切口设置在烟囱50.5 m处，此位置外径为5.6 m、壁厚0.24 m，重量为322.37 t，重心高度为18.8 m。

(2)切口高度

切口高度是保证定向倒塌的一个重要参数。一般情况下[1]，爆破切口的高度通常取为h=(1.5～2.0)δ。为确保爆破时烟囱按预定方向准确倒塌和减小爆堆范围，实际工程中切口高度通常取大于切口位置的壁厚5倍以上，因此得出其下部切口h=5.0×0.36=1.8 m，取3 m；烟囱上部切口取h=5×0.24=1.2 m，考虑上切口打眼施工困难，实际取1 m。

(3)切口长度

烟囱倒塌方向和爆堆范围较大地受到切口长度的影响。为取最佳的切口长度，应根据式(1)进行取值

(1)

式中：L为爆破切口长度；s为烟囱爆破部位的外周长。

烟囱的爆破切口圆心角取α=210°，下部的切口长度取14 m，上部切口长度取10 m。

(4)上下切口的起爆时差

折叠爆破达到最佳效果应当满足：保证下切口起爆时，防止上、下段筒体间出现倾倒方向偏差。

通过计算切口高度可知，在切口闭合瞬间，上段筒体重心在切口水平面的投影到塔心的距离大于或等于该处半径[10]，因此，起爆时差为

(2)

式中：φ为烟囱与Y轴的夹角；J1为转动惯量；L1为烟囱计算长度；Δt为经验值，一般取100～500 ms(筒体材料强度高时取小值)。

目前，国内上、下爆破切口的起爆时差选1.4～7.0 s，根据理论和工程经验分析得出[7]，实际爆破采用半秒6段雷管，即在上部爆破烟囱形成5°的倾斜时下部切口开始起爆[11]，上部与下部的起爆时差约为2.5 s。

3 烟囱倾倒过程的动能分析

烟囱折叠倒塌过程中形成了铰接双连杆折叠下落的现象，为双自由度动力学的问题，采用拉格朗日方程建立动力学模型[12]。见图2。

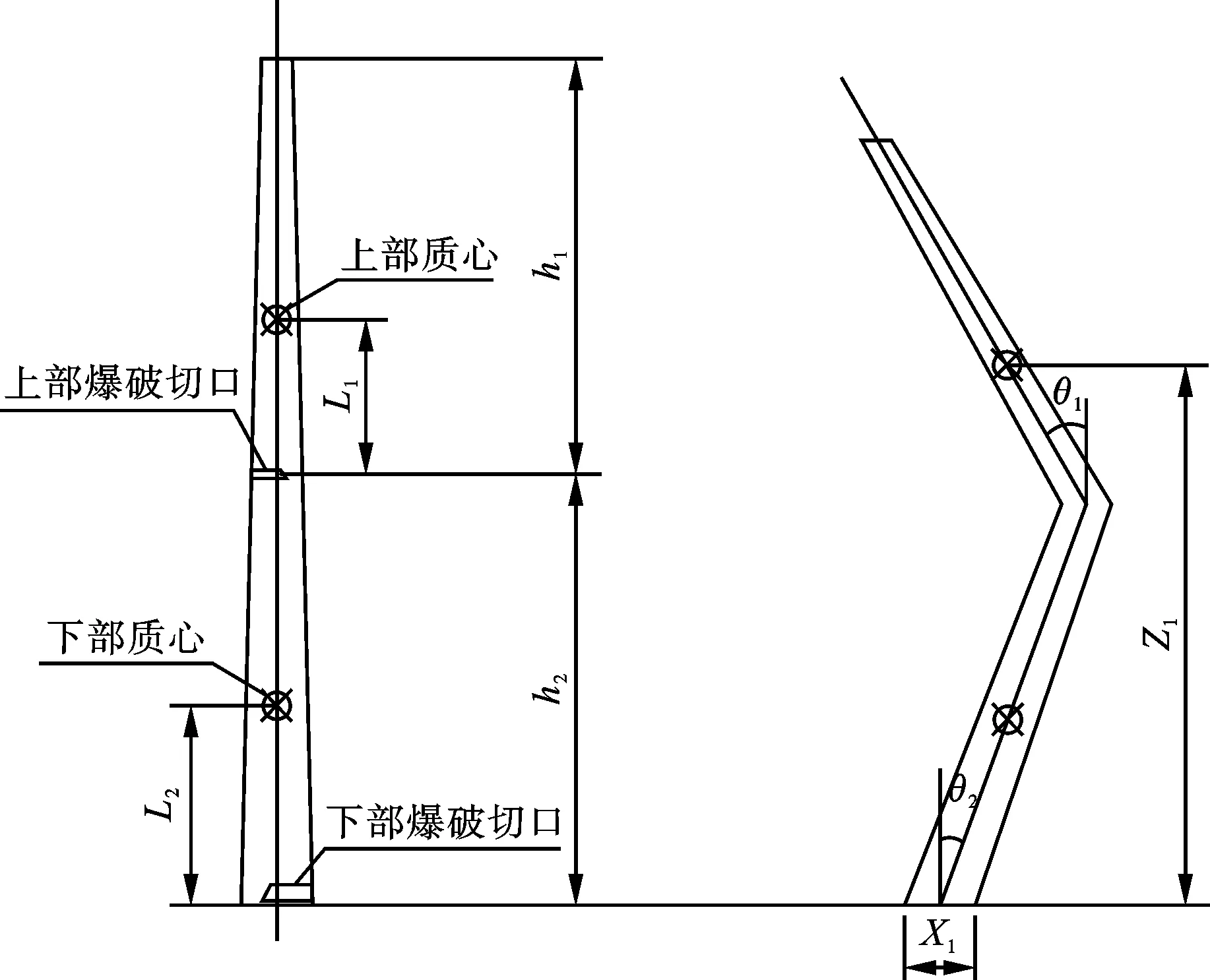
图 2 烟囱折叠倒塌过程图Fig. 2 Schematic diagram of the collapse of the chimney

(1)上段筒体的几何学关系

x1=h2·cosθ2-L1·sinθ1

(3)

Z1=h2·cosθ2+L1·cosθ1

(4)

式中：X1为烟囱上段质心水平位移；Z1为烟囱上段质心垂直位移；h1为上段筒体长度；h2为下段筒体长度；L1为上段筒体质心到上部切口的距离；L2为下段筒体质心到下部切口的距离；θ1为上段筒体转角；θ2为下段筒体转角。

将X1，Z1进行微分，可得出烟囱上段质心水平向及垂直向速度分量，从而得出上段平动部分动能

(5)

(6)

(7)

m1为上段筒体的质量，而上段绕其重心转动的转动部分动能为

(8)

J1c为上段绕其质心的转动惯量。

由式(7)和式(8)两式可得上段的总动能为

(9)

(2)下段筒体的动能为

(10)

J2为下段筒体绕其质心的转动惯量。

(3)从而得到运动过程中系统的总动能为

T=T1+T2

(11)

(12)

4 计算模型

采用SolidWorks建立精准三维立体模型，之后导入到Hypermesh软件中对其进行细化处理。利用Hypermesh软件强大的网格划分功能，对模型网格进行加密划分。考虑到烟囱模型关键地方的约束较多，后期需要添加大量的约束，采用直接法建立钢筋混凝土共节点分离式模型[13]，将钢筋节点与混凝土节点直接产出单元体。模型材料参数设定中，钢筋设置为BEAM161，混凝土设置为SOLID164 实体单元。据钢筋混凝土结构的力学特征研究得出，将混凝土模型设置为* MAT_BRITTLE_DAMAGE ，混凝土的弹性模量为20 GPa，泊松比为0.2，拉伸极限强度为5.0 MPa，剪切极限强度为6.0 MPa，钢筋模型设置为*MAT _ PLASTIC _KINEMATIC ，其密度为7825 kg /m3，弹性模量为200 GPa，泊松比为0.25，屈服强度为335 MPa，爆破切口失效模型设置为* MAT_ADD_EROSION，将钢筋的抗拉失效应变定义为0.15。

通过修改关键字中的CONTROL_TIMESTEP中的DT2MS控制计算时间，当DT2MS>0时，模型中离散的所有小单元都会以软件内部设定好的时间步长进行计算，全部的小单元都会被质量缩放。当DT2MS<0时，并不是所有的小单元都会质量缩放了，只有时间步长小于DT2MS的单元才会被质量缩放[14]。

5 上下切口最佳延时时差研究

前面已经对该爆破过程进行了数值模拟，模拟结果与实际爆破结果高度一致。在此基础上对其进一步研究，分别设置上下切口的起爆时差为1s、1.5 s、2 s、2.5 s、3 s，通过爆堆最远距离、烟囱倒地破碎程度和烟囱触地速度这三个变量对起爆时差进行优化。

(1)倒塌过程的对比(见图3)

图 3 不同起爆时差下的倒塌过程模拟效果比较Fig. 3 Comparison of simulation effects of collapse process with different delay time

通过对比分析图3，可以看出随着上下切口起爆时差的增长，烟囱上半段的倒塌角度越小，上半段触地的时间越晚。分析倒塌过程图可以看出上部爆破切口部分的闭合受到下部爆破切口的影响，当上下部爆破切口的起爆时差相差较小时，烟囱上下两段的倒塌方向相反。烟囱下半段倒塌会通过爆破切口保留部分的烟囱向反方向拉动上半部分，导致上半部分落地速度较快。当起爆时差为3 s时，上部和下部爆破切口起爆时差相差较大，上部烟囱爆破切口部分的钢筋混凝土已经被拉坏，下半段烟囱对上半段的倒塌速度影响较小，上部分烟囱断裂后下部分烟囱才开始倾斜，是两个独立的爆破过程。上下部烟囱爆破倒塌没有衔接起来，会导致爆破倒塌方向的不确定性增大[15]。

(2)爆堆倒塌最远距离的对比

通过分析图4不同起爆时差下的爆堆范围及倒塌最远距离得出不同起爆时差下的烟囱触地后基本破碎，只有起爆时差为2.5 s时的倒塌最远距离最小为50 m，其他起爆时差的倒塌最远距离均为55 m左右。因此起爆时差为2.5 s时的倒塌范围是最小的，即为最安全的爆堆范围。

(3)烟囱触地速度的对比

通过图5不同起爆时差下的烟囱触地速度可以分析得出：最大触地速度发生时刻随着起爆时差的增大而越来越大，起爆时差为1 s、1.5 s、2 s、2.5 s、3 s下的最大触地速度出现时刻分别为6.5 s、6.9s、7.5 s、7.9 s、8.2 s，同时证明图3中得出的随着上下切口起爆时差的增大触地时间越来越晚的结论正确。起爆时差为1 s的烟囱整体最大触地速度为16 m/s，其余起爆时差的最大整体触地速度随起爆时差增大而逐渐减小。

6 数值模拟结果及分析

分析各项指标，双向折叠倒塌爆破的上下切口的最优起爆时差为2.5 s，和爆破设计的公式计算得出的上下爆破切口的起爆间隔时差相同。图6显示了烟囱倒塌与工程实际的比较，数值模拟结果精确仿真了工程实际的倒塌过程。烟囱倒塌的方向也按照爆破设计的方向倒塌，折叠爆破实现了减小爆堆范围的要求。0 s时上部爆破切口起爆，在重力作用下开始向着爆破切口方向倾斜。2.5 s时下部爆破切口起爆，此时上部烟囱大概倾斜了5°，减小了烟囱出现前冲现象的概率。4.2 s时上下段的烟囱倾斜角度不断加大，倾斜速度不断加快。6.6 s时近乎自由落体式的速度触地破坏，实际的烟囱倒塌过程与数值模拟计算相同时刻的烟囱倒塌的过程基本一致。

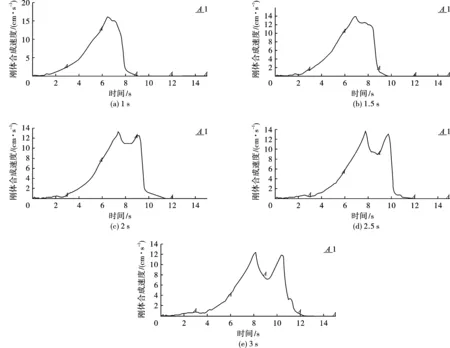
图 5 不同起爆时差下的烟囱整体触地速度Fig. 5 The overall velocity of the chimney touching the ground with different delay time

图 6 实际爆破效果与模拟效果的比较Fig. 6 Comparison of actual blasting effect and simulation results

结合数值模拟的结果可以将烟囱的倒塌过程分为三个阶段：第一阶段为上切口的形成至保留区出现裂缝的阶段；钢筋和混凝土共同承担上部烟囱的压力作用、上部切口形成而产生弯矩，出现拉应力作用。此时处于弹性阶段，应力与应变呈现线性正比例关系。随着弯矩的增大，爆破切口保留处的应变也越来越大，由于混凝土抗拉强度远小于抗压强度，混凝土在拉应力作用下开始出现塑性变形，但钢筋弹性模量较大，其仍然属于弹性阶段[16]。当上部切口保留处的拉应力大于混凝土所能承受的最大拉应力时，爆破切口保留处开始出现裂缝。裂缝的出现标志进入第二阶段，随着弯矩和变形的增加混凝土逐渐退出工作，在受拉钢筋达到屈服之前，所有的拉应力由钢筋承担。接下来进入破坏阶段，为第三阶段，钢筋达到屈服值以后进入强化和颈缩阶段，此时裂缝快速变大、上部烟囱倾斜角逐渐增大直到从爆破切口处断开触地破坏，下部切口爆破后也会产生和上部切口相同的三个阶段[17]。

7 结论

(1)基于LS-DYNA联合Hypermesh的数值模拟方法对100 m高钢筋混凝土烟囱的双向折叠爆破进行了仿真模拟，数值模拟的结果与工程现场数据高度一致。

(2)分析了烟囱倒塌的触地快慢受到起爆时差的影响，得出起爆时差越大，触地时间就越晚的结论。同时起爆时差越大，上部爆破切口倒塌方向的爆堆就越大。爆破时差为2.5 s时的爆堆堆积范围是最小的。

(3)分析了烟囱的触地速度，得出整体触地速度越快对地面的振动也就越大，越不安全的结论。分析得出起爆时差为1 s时的烟囱整体触地速度最大为16 m/s，其余起爆时差下烟囱整体触地最大速度随起爆时差增大而逐渐减小。也就意味着起爆时差越大对地面的振动越小，越有利于周边建筑物的安全。

(4)综合分析模拟结果，爆破时差为2.5 s时爆堆的范围最小，烟囱整体倒塌触地速度也相对较小为13.8m/s，爆堆破碎程度与时差影响关系不明显，所以2.5 s是最佳的起爆时差。从而也证明了爆破时差计算公式是正确可行的，对类似的爆破工程具有一定的指导意义。