基于协同仿真方法的U型橡胶结构涡致振动研究
熊小慧, 唐明赞,*, 汪海燕, 朱 亮, 李小白
(1. 中南大学 轨道交通安全教育部重点实验室, 长沙 410075; 2. 中南大学 轨道交通安全关键技术国际合作联合实验室, 长沙 410075; 3. 中南大学 轨道交通列车安全保障技术国家地方联合工程研究中心, 长沙 410075; 4. 中车青岛四方机车车辆股份有限公司, 青岛 266111)
0 引 言
U型橡胶结构外风挡被广泛应用于高速列车两车厢端部连接处,如图1所示,使车体表面光顺平滑过渡,以此来减小列车运行时的气动阻力与气动噪声[1-3]。近年来,随着旅客列车向高速化、轻量化方向发展,结构设计中被忽略的气动弹性问题逐渐突显出来。当列车高速运行时,列车表面周围空气的流速急剧加快,运动的空气以列车风的形式作用于外风挡上,对U型橡胶结构产生沿流向的阻力(拉力)和垂直于流向的升力,风产生的压力或U型橡胶外风挡上旋涡的脱落均可能诱发结构产生以流固耦合作用为特点的变形或振动现象[4-5]。而外风挡的变形振动反过来又影响周围流场运动,从而改变气动载荷的分布和大小,将导致车厢端部连接处的气动力分布不均匀,严重影响列车行车稳定性。同时,外风挡的变形振动对于结构的疲劳寿命同样产生危害。因此对于高速列车U型橡胶结构外风挡的气动弹性研究显得尤为重要。

图1 高速列车U型橡胶结构外风挡
气动弹性其本质是气动力、弹性力以及惯性力之间相互耦合作用发生在两交界面上的流固耦合问题[6-7]。在工程领域,除了航空航天工程中的飞行器结构外,民用工程领域的桥梁、烟囱、高塔、高楼等高耸结构,机械工程领域的涡轮机械以及电力工程领域的输电线等,都存在流固耦合问题[8-11]。对于此类较复杂结构流固耦合的研究,主要采用风洞试验与数值计算方法。随着计算机软硬件技术的迅速提高,数值模拟方法已发展成为分析流固耦合作用的重要工具[12-13]。周岱等采用了弱耦合分区法模拟了不同雷诺数下单圆柱横向和两向流致振动、串列双圆柱两向流致振动,分区弱耦合算法计算效率较高,但难以克服强附加质量效应,易导致数值失稳[14-15]。强耦合分区算法在每时间步内依次迭代计算各单场方程直至收敛,具备良好的物理守恒性和程序模块性[16]。对于低质量比、大位移或柔性体等复杂情形可采用分区强耦合算法进行求解。并且基于分区强耦合的模块化优势,运用商业软件计算流固耦合问题具有广阔的工程应用潜力[17-18]。
高速列车U型结构外风挡采用橡胶材料,相同的工作环境下,其强度与刚度均低于金属材料,在气动载荷作用下U型橡胶结构更容易出现大变形及振动问题。关于橡胶材料的有限元分析,软件Abaqus具有较完备的材料模型,而软件STAR-CCM+对于流体的建模仿真具有较好的分析能力。因此,需要构建软件之间的协同仿真环境,以充分发挥各仿真平台的优势,并消除在单一平台中进行仿真的局限性[19]。
目前,尚未有研究采用STAR-CCM+和Abaqus相结合的方法,对高速列车U型橡胶结构外风挡以及车体其他部件的气动弹性问题进行流固耦合分析。为了验证该协同仿真方法的可行性,本文利用高速列车上拆卸的U型橡胶结构试件进行风洞试验,并根据风洞试验构建仿真模型,其目的为了说明该流固耦合协同仿真方法能否较好的分析U型橡胶结构在气动载荷作用下的变形振动问题。在本次U型橡胶结构试件协同仿真中,研究了不同空气流速条件下U型橡胶结构变形及振动情况,探讨了U型橡胶结构振动频率与空气旋涡脱离频率的相互关系。关于高速列车整车外风挡气动弹性问题尚未有研究,此基于流固耦合协同仿真的U型橡胶结构试件的试验研究,是为下一步整车外风挡结构气动弹性问题研究做的基础性工作,可利用该协同仿真方法去分析列车不同运行工况下外风挡的气动响应状态,为高速列车外风挡设计及应用评估提供分析方法与技术支撑。
1 流固耦合理论基础
在流固耦合分析中,常用耦合方法有直接耦合法和分区耦合法[20]。直接耦合法可同步直接求解耦合方程,但由于流固耦合问题中高度的非线性特征,很难在一种网格体系中用一种格式同步推进求解,导致在实际应用中存在局限性。分区耦合法最大限度地保持了流体与固体之间的独立性,能够充分利用现有的计算流体力学(CFD)和计算固体力学(CSD)的方法和程序,加上数据交换模块,减少了计算复杂度、简化了隐式/显示的处理、有利于子循环求解、程序模块化等优点,使得分区耦合法在流固耦合问题中有了广泛的应用。图2所示是一个典型的流固耦合问题,将计算域分为流体区域和固体区域,其中流体模型和固体模型的材料属性、边界条件等分别定义,并且在两个模型的交界面发生相互作用,通过耦合求解获得流体和结构的响应。

图2 流固耦合模型
1.1 动力学与运动学条件
固体模型基于拉格朗日坐标系,流体模型通常采用欧拉坐标系。而对于流固耦合问题,由于流固界面是可变形的,因此流体模型必须建立在ALE(任意拉格朗日-欧拉)坐标系上。并且流体模型与固体模型分区进行计算,其相互作用在交界面上需满足运动学和动力学条件[21]。
其流固耦合交界面的运动学条件(或位移相容性)为:
其流固耦合交界面的动力学条件(或牵引力平衡)为:
流体速度条件是由运动学条件决定,其方程为:
在流体域耦合界面上的节点位置由运动学条件决定,其他流体域节点的位移可由程序自动确定,以保持计算网格质量,然后求解其ALE公式中的流体流动控制方程。
根据动力学条件,流体牵引力沿流固耦合界面整合成流体力,施加于结构节点上,其方程为:
其中hd为固体位移的虚量。
1.2 双向耦合的迭代计算
耦合分区法中的双向耦合迭代计算不断利用耦合系统中流体(或固体)场求解变量提供给固体(或流体)场进行连续迭代求解[22]。

①从流体方程中求解流体节点解向量
此解向量利用固体模型中的节点位移在流体流动分析中得到,固体位移松弛因子λd(0<λd<1)。压力向量解的残差满足判别条件。
②从固体方程中求解固体节点解向量
流体压力松弛因子λτ(0<λτ<1)。
③在指定的耦合边界条件上计算流体节点的位移为:
④压力和位移迭代解还没有收敛,则程序返回到步骤①并继续进行下一个迭代。在这种求解方法中,时间步长和求解时间由流体模型控制,并确定了控制耦合系统收敛的参数。这些参数包括压力和位移公差、松弛因子、收敛准则等。
1.3 STAR-CCM+与Abaqus协同仿真方法
软件STAR-CCM+和Abaqus协同仿真方法建立在双向耦合迭代计算的基础上,利用SIMULIA协同仿真引擎在两个软件之间以耦合步间隔自动交换数据,这种协同仿真技术相对于文件交换方法的耦合更强。在协同仿真耦合步中,Abaqus优先计算,即图3协同仿真流程图中灰色部分为一个耦合步。
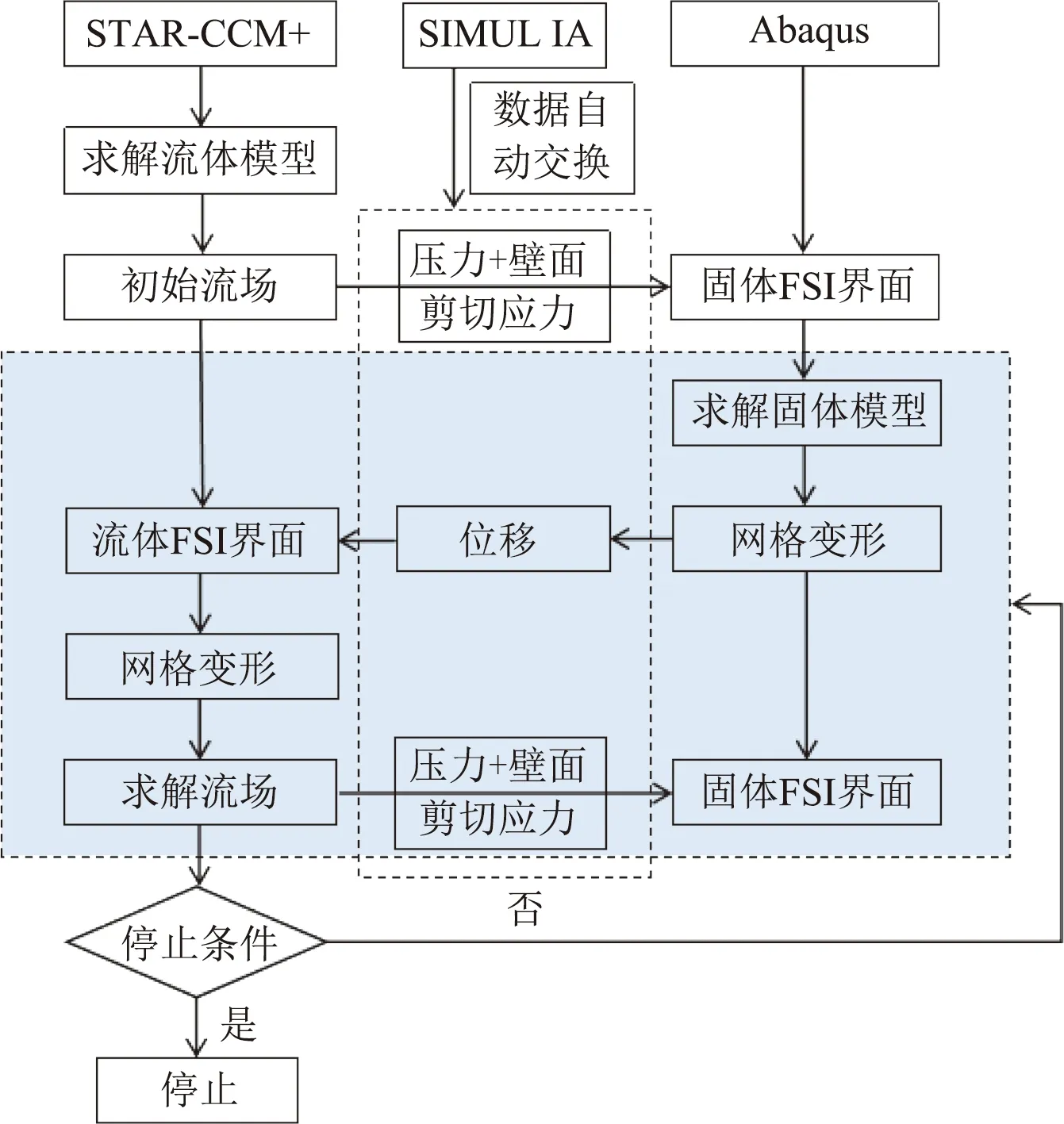
图3 STAR-CCM+和Abaqus协同仿真流程
2 U型橡胶结构协同仿真建模及验证
为验证STAR-CCM+与Abaqus协同仿真方法的可行性,利用U型橡胶结构外风挡试件在风洞进行压力位移测试,再根据风洞试验进行流固耦合协同仿真分析,比较风洞试验和数值计算的测试点压力、位移以及变化频率,并基于流固耦合协同仿真方法分析了不同速度等级下U型橡胶结构变形及振动情况。
2.1 U型橡胶结构风洞试验
风洞试验中,在U型橡胶结构表面布置压力传感器测量表面压力变化,并使用红外线激光位移计对橡胶变形振动进行测量,风洞试验传感器布置如图4(a)所示。U橡胶结构的固有动态特性由模态试验所得,试验如图4(b)所示。力锤法模态试验测量的一阶固有频率为7.29 Hz,二阶模态16.59 Hz,三阶模态23.54 Hz。

图4 风洞试验测点布置
2.2 建立协同仿真计算模型
根据风洞试验中的模型及工况建立流固耦合协同仿真模型。该外风挡试件以EPDM(三元乙丙橡胶)为基材,通过一系列工艺处理得到现U型结构,其材料试验所得该试件杨氏模量6 MPa,泊松比0.4995,密度1300 kg/m3。
1) 计算模型及测点布置。图5所示为U型橡胶试件计算模型及测点位置,为了便于数值仿真与风洞试验结果的比较,计算模型的尺寸参数以及工艺孔位置与风洞试验试件一致,其中压力测点p1’和位移测点d1’的位置与风洞试验测点布置一致,空间压力测点p2’用于分析U型结构上空气旋涡脱离的频率。

图5 计算模型及测点布置
2) 模型离散化。STAR-CCM+和Abaqus协同仿真分析中,需要准备流体和固体两个计算模型,几何一致且相对于坐标轴处于同一坐标位置。图6(a)为Abaqus软件中固体模型的网格,采用C3D8RH单元;图6(b)为STAR-CCM+软件中流体计算区域部分壁面网格示意,在近U型橡胶结构区域进行网格加密并在结构表面和风洞壁面都设置附面层。

(a) 固体模型离散
3) 计算区域及边界条件。计算区域的尺寸与风洞试验的试验区段尺寸一致,断面宽1 m,高0.8 m。计算区域速度入口为均匀风速来流,四面设为壁面,为避免压力出口对所关心区域流场结构的影响,并保证区域内流场的充分发展,压力出口设置较远,速度入口到U型橡胶结构壁面为3 m,U型橡胶结构壁面到压力出口为6 m。U型橡胶结构的固定边界与风洞安装支架的固定方式相同。计算区域及边界条件的设置如图7所示。
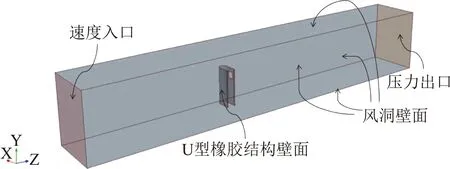
图7 流场计算区域及边界条件
4) 模型参数设置。在STAR-CCM+中设置流场计算模型,采用三维非定常黏性不可压缩k-ω湍流模型,网格变形基于RBF(径向基函数)方法,二阶精度时间离散,耦合时间步长0.001 s,并设置内迭代10次,速度入口空气流速分别为20 m/s、30 m/s、40 m/s。
在Abaqus设置中,杨氏模量6 MPa,泊松比0.4995,密度1300 kg/m3,瑞利阻尼alpha=0.125,beta=0.00159,采用动隐式求解,耦合时间步长0.001 s,并设置内迭代10次。并将Abaqus中固体模型的配置参数,输出“.inp”文件,在STAR-CCM+中的联合仿真设置中指定该文件路径。
2.3 数值计算方法验证
数值计算中压力测点p1’在不同风速下的平均值与风洞试验该测点位置的压力平均值如表1所示,位移测点结果如表2所示。由于U型橡胶结构在不同风速的作用下产生变形振动,为了比较测点的响应过程,选取30 m/s风速条件下,位移测点风洞试验与数值计算中的弯曲变形振动时程曲线进行比较,并进行了功率谱分析,如图8所示。
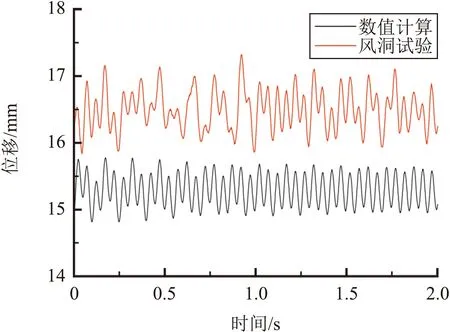
(a) 位移测点振动时程曲线
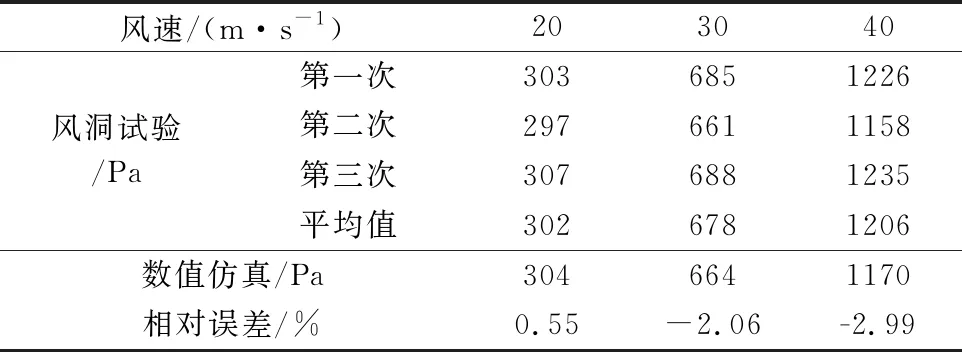
表1 U型橡胶结构表面压力测点结果

表2 U型橡胶结构表面位移测点结果
通过表1中数据可以看出:风洞试验压力监测点p1的结果重复性较好,将三次风洞试验测量数据求取平均值并与仿真计算结果进行比较,在风速为40 m/s条件下数值计算与试验的压力最大相对误差为2.99%。因此,对压力场的计算该仿真方法具有一定的可靠性。
在表2中,通过对比位移测点的仿真计算与风洞试验结果可以发现,数值计算结果相对偏小,并且随着风速的增大,相对误差随之增大,当风速达到40 m/s时,相对误差为8.92%。从位移比较结果来看,该流固耦合协同仿真方法用来研究U型橡胶结构振动变形具有一定的可靠性。
通过表2与图8可以得出,30 m/s风速条件下,风洞试验位移测点的平均位移为16.5 mm,振动主频为20.1 Hz;数值计算的平均位移为15.3 mm,振动主频为20.5 Hz。风洞试验与数值计算的位移相对误差为7.27%,属于工程应用可接受范围。
3 计算结果及讨论分析
3.1 不同速度等级下结构位移及频率
不同风速条件下结构由静止到振动平稳,测点d1’的计算全过程位移时程曲线如下图9所示;取0~2 s时间段位移做功率谱分析如图10所示;取4~6 s时间段位移做功率谱分析如图11所示。
不同风速条件下位移测点d1’在0~2 s和4~6 s内两个阶段的振动主频以及平均位移见下表3所示。
由图9中可以看出,U型橡胶结构受到风载荷作用由静止产生弯曲振动。在0~2 s时间内,结构受气动力、弹性力、惯性力以及阻尼的作用,弯曲振动的振幅逐渐变小。并且随着风速的增加U型橡胶结构产生的变形位移量越大。在4~6 s时间内,U型橡胶结构维持在弯曲变形状态下等幅振动,且风速越大,振动幅值越大。

图9 不同速度等级下测点d1’的位移时程曲线
通过图10和图11中及表3中得出:1) 在0~2 s时间内,风速为20 m/s、30 m/s及40 m/s条件下U型橡胶结构振动主频分别为7.0 Hz、7.2 Hz和7.5 Hz。而该U型结构的一阶弯曲固有频率为7.29 Hz,因此,在不同速度等级下,结构受到气动力作用由静止产生变形振动,其振动特点为该结构产生以接近自身一阶弯曲固有频率的弯曲振动。(2)在4~6 s时间内,U型橡胶结构在气动力、弹性力、惯性力以及结构阻尼的作用下变形弯曲振动幅值变小,其结构处于一定弯曲变形状态下的振动,风速为20 m/s、30 m/s及40 m/s条件下U型橡胶结构振动主频分别为7.0 Hz、20.5 Hz和26.5 Hz。

表3 测点d1’的平均位移及振动主频

图10 不同速度等级下测点d1’的位移功率谱分析(0~2 s)

图11 不同速度等级下测点d1’的位移功率谱分析(4~6 s)
3.2 涡脱频率与结构振动关系
图12为不同速度等级下空间监测点p2’的压力时程曲线和压力功率谱。表4中为测点p2’的压力功率谱变化主频和4~6s时间内U型橡胶结构位移测点d1’的振动位移主频。
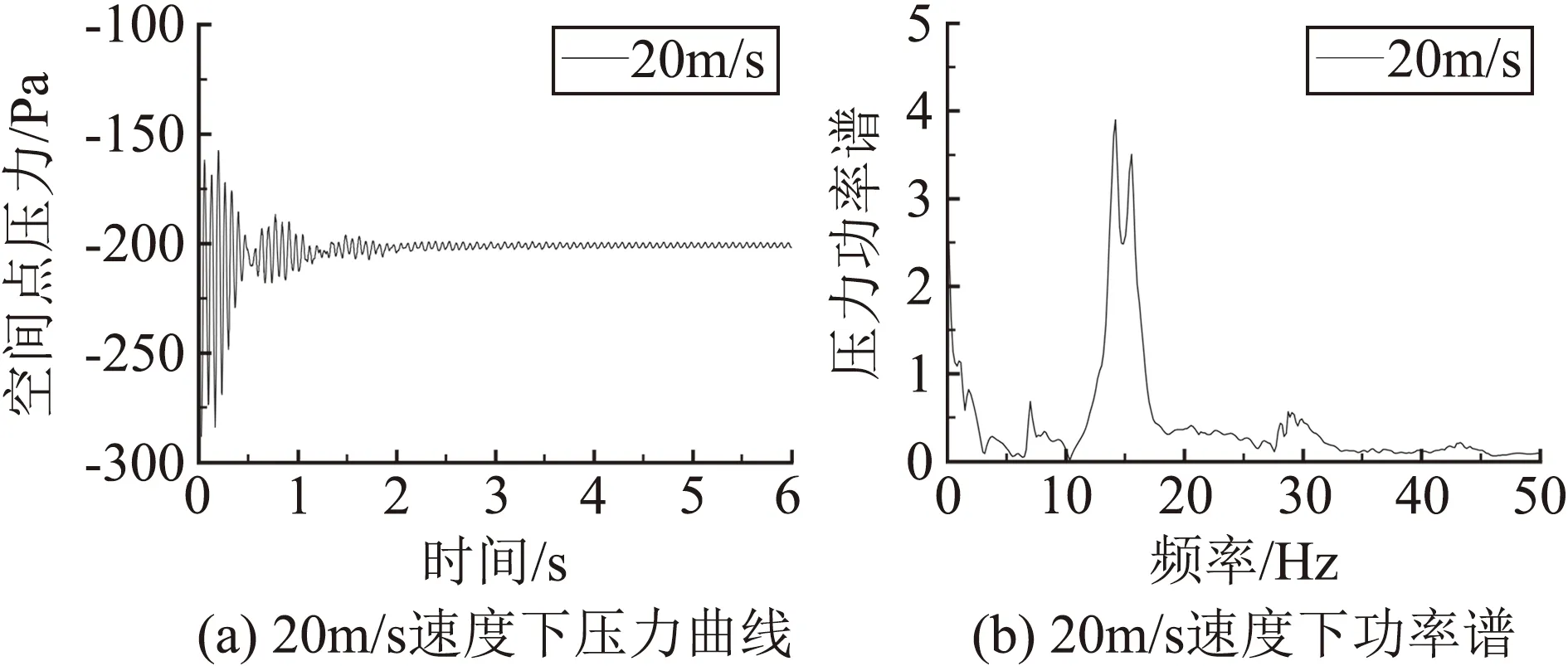
图12 不同速度等级下空间点的压力时程曲线及功率谱

表4 涡脱频率与结构振动主频
由图12中可以看出,测点p2’处的压力变化随风速变化明显,压力变化幅值随风速增加而增加。压力变化频率明显随风速的增加而增大。
在4~6 s时间内,U型橡胶结构的振动受旋涡脱落的影响产生高频振动,当风速较低时,旋涡脱落的湍动能较小,不足以强迫结构产生与涡脱频率相同的振动,因此20 m/s风速下空间点压力变化频率为14.2 Hz,而U型结构振动频率为7.0 Hz;而当风速较大时,涡脱频率强迫结构做相近频率的振动,如30 m/s风速下空间点压力变化频率为20.2 Hz,而U型结构振动频率为20.5 Hz。
3.3 流场压力与速度矢量云图
图13、图14所示分别为速度入口30 m/s风速条件下,U型橡胶结构处于4~6 s时间内的流场压力云图及矢量云图。
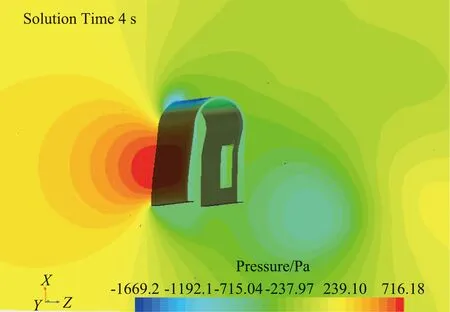
(a) t=4.0 s
压力云图及矢量云图展示旋涡的产生、发展及脱离。由图13中可以看出,在U型橡胶结构的圆弧部位可以观察到涡的产生,随着时间的推移,逐渐从圆弧顶部脱离,并沿着流场方向向后发展,从而导致圆弧部位的摆动。图14矢量云图中通过速度矢量显示了涡的旋转方向及流动方向,旋涡的产生和脱离导致弧顶部位产生摆动,形成U型橡胶结构的涡致振动现象。
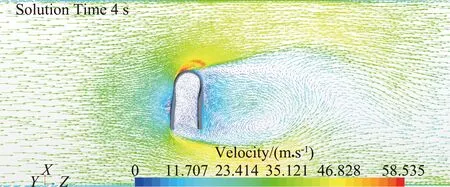
(a) t=4.0 s
4 结 论
本文基于STAR-CCM+和Abaqus协同仿真方法,研究了不同空气流速条件下U型橡胶结构变形及振动情况,探讨了U型橡胶结构振动频率与空气旋涡脱离频率的相互关系。并利用U型橡胶结构试件风洞试验,验证了该协同仿真方法用于研究此类问题的可行性。得到的主要结论有:
1) STAR-CCM+和Abaqus协同仿真方法对于橡胶结构大变形振动问题的研究满足工程应用要求,具有一定的可靠性。
2) U型橡胶结构受到气动载荷作用由静止产生弯曲变形,风速越大其结构产生的弯曲变形量越大。气动力作用下结构弯曲变形同时产生弹性力、惯性力以及阻尼力,各作用力相互耦合导致结构产生振动,其振动特点为接近该结构自身一阶弯曲固有频率的弯曲振动。
3) 当结构受到气动力、弹性力、惯性力趋于平衡,其结构处于一定弯曲变形状态下的振动。风速较低,旋涡脱离的能量不足以强迫U型橡胶结构的振动与涡脱频率相一致。随着风速的增大,U型橡胶结构的振动是由旋涡脱离导致的受迫振动。
——以徐州高层小区为例

