通过二次指数平滑构建生猪价格短周期量化模型的方法与预测效果评估

杨雪 李文献

摘 要： 基于供需逻辑设计的长周期量化模型对生猪价格趋势变化及周期判断无法在短期内完全体现，因此为提高预测对市场变化的响应速度，更准确地判断周期进程，设计短周期量化模型具有重要意义。本文主要通过二次指数平滑方法构建生猪价格短周期量化模型来预测本轮猪周期生猪价格，且在二次指数平滑及衰减趋势方法的基础上，设计综合评估指数，比较多种参数确定方法从而选择最优值，输出多组初始预测值，进一步设计加权方法计算加权预测值和预测带，模型预测效果良好，可为生猪价格短期预测提供参考，与长周期模型形成互补。

关键词：生猪市场 二次指数平滑 价格预测

一、前言

2018年8月以来，非洲猪瘟严重影响生猪生产效率，推动了新一轮猪周期的产生，生猪价格大幅波动，本文对分析生猪价格规律预测趋势变化具有重要意义。杨雪和李文献根据供需价格理论分析设计主因（非洲猪瘟）量化模型（Quantitative model of hog price cycle caused by African Swine Fever，QM-ASF），预测月度价格趋势，将本轮猪周期划分为主因影响期、供应减少期、产能恢复期、产能释放期、产能调整期和成本竞争期六个阶段。又通过对生产区与消费区在猪周期进程中价格变动的差异性分析，设计生猪调运指数，反映供需变化和所处猪周期阶段，预测生猪价格走势，对QM-ASF的预测提供补充与预警信息。但QM-ASF作为长周期模型，其预测判断无法在短期内完全体现，调运指数的预警作用也需要通过一段时间的观察再确定，仅依靠上述两种方法无法及时判断生猪价格变化和周期的起点与终点。而短周期量化模型具有对序列变化响应及时的优势，可以迅速反映当前市场价格变化，进而分析现阶段价格规律，为市场供需变化和猪周期阶段变化提供更具体的判断。本文设计二次指数平滑多期加权预测模型（Multi-period weighted quadratic exponential smoothing，QES-W），对本轮猪周期生猪价格进行预测并评估其效果。

Robert G和Brown提出的指数平滑法 （Exponential Smoothing，ES）认为时间序列的态势具有稳定性或规则性，因此时间序列可以顺势推延，即最近的态势会在未来持续。ES模型适用于水平型的序列，二次指数平滑模型（Quadratic Exponential Smoothing Model，QES）适用于具有趋势性的序列。马丽娜采用QES模型研究蔬菜价格变化趋势，结果显示其具有较强的预测分析能力。根据对时间序列发展中趋势是完全延续还是逐渐减弱的研究，Gardner和McKenzie进一步提出了衰减趋势方法（Damped trend methods），认为趋势不会随着时间增加而无限增长或减少，而是逐渐衰减，即时间价值会损失。王玉明等通过衰减趋势的QES模型较好地预测了黑热病发病数。

本文将衰减趋势的QES模型应用于生猪价格的趋势分析，且不同于以往研究仅选择固定的预测期长度（Predictive Step Length，l）计算单一预测值（冯金巧等），本文选择不同的预测期长度计算多组预测值对未来1至l期的价格进行预测，同时进一步设计加权方法计算加权预测值以缩小预测误差。

二、二次指数平滑多期加权模型（QES-W）整体构架与计算方法

（一）模型设计框架

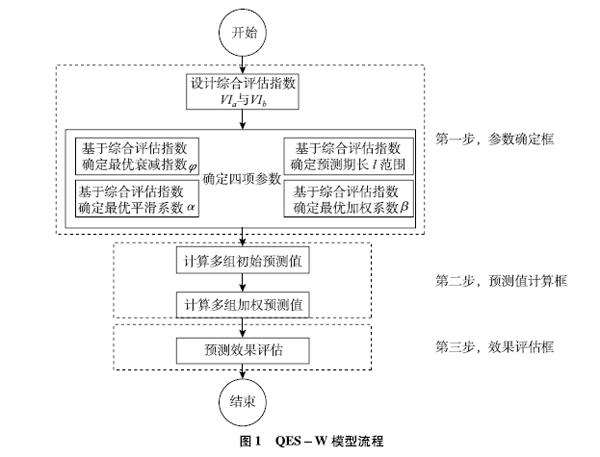
QES-W模型流程如图1所示。

（二）計算方法

QES-W模型设计包括参数确定、预测值计算和效果评估三部分内容（见图1），其中预测值计算是模型的核心内容，参数确定是提高模型预测值预测效果的方法，效果评估是对模型实际应用时预测效果的验证。

预测值的计算分为初始预测值和加权预测值两部分，初始预测值的计算如下。

式中，y︿t+l|t表示t时刻对t+l时刻的预测值，yt表示t时刻的观测值。at表示t时刻的基线水平值，bt表示t时刻的趋势因子值，kl表示预测期长l的时间价值。

本文进一步设计加权方法，通过多组不同的初始预测值计算对应的加权预测值，缩小预测误差：

式中，y︿t+l|t+l-i表示在t+l时刻的i期之前对t+l时刻的初始预测值，y︿t+n表示通过加权系数βi将多组t+l时刻的初始预测值计算后的加权预测值，n=l。

模型中涉及四项关键参数，初始预测值的计算与衰减指数φ、预测期长l、平滑系数α共三项参数有关，加权预测值的计算与加权系数βi有关。

衰减指数φ主要用来衡量时间价值kl随着预测期长l的增加而损失的程度，取值范围0<φ≤1，Gardner和McKenzie研究发现，φ过小则衰减效果太强，与趋势延续假设相悖，而φ过大则近似无衰减，因此应用衰减模型时通常限制080≤φ≤098。本文对上述范围内的φ进行检验，最终确定预测效果最优的φ。

预测期长l可以衡量模型预测期的长短，表示t时刻对t+l时刻的预测，l越大，可预测得越远，同时预测效果也随之下降。冯金巧等通过优选误差最小的预测期长l来确定最终的取值，本文则是分析l增加过程中预测效果的变化，判断预测效果达到通过标准条件下l的最大值，依次确定l的取值范围，使模型可以计算多组不同的初始预测值。

平滑系数α决定预测模型对实际观测值变化的响应程度，取值范围0≤α≤1，α越大，预测值对最新观测值的变化越敏感。冯金巧等采用定常系数方法，通过优选误差最小的平滑系数α来确定最终的取值。盖春英和裴玉龙应用自适应动态系数方法使平滑系数随序列变化而调整。本文分别对两种方法进行检验，比较后选择预测效果更优的方法确定α。

加权系数βi决定初始预测值在加权预测值计算中所占的权重，加权计算时既可以选择全期加权，又可以选择移动加权，本文分别对这两种加权方法进行检验，选择加权后预测效果更优的方法确定βi。

参数确定需要比较不同参数条件下的预测效果，预测效果评估的内容包括相关系数r、拟合优度R2、平均绝对误差MAE、平均绝对误差百分比MAPE、误差均方MSE和误差均方根RMSE这六项指标。r和R2从趋势拟合度角度评估预测效果，取值在0～1，值越大代表预测效果越好;MAE、MAPE、MSE和RMSE从误差大小角度评估预测效果，值越小代表预测效果越好。定义指标标准值作为预测效果是否良好的判断依据（见表1）。

经过六项指标的初步评估后，为直观表现参数对预测效果的影响，本文设计了综合评估指数，包括预测值的综合评估值VIa和预测带的综合评估值VIb。VIa选择 r衡量拟合度，赋值为正，选择MAE、MAPE和RMSE的达标百分比（即各自实际值除以标准值）的平均数衡量误差大小，赋值为负，计算如下。

由于模型根据不同预测期长l产生了多组预测值，除检验每组预测值的预测效果外，还可通过预测带准确性（Probability of Accuracy，PA）和预测带带宽（Width of Predictive Band，PW）对多组预测值构成的预测带效果进行检验，定义预测带的综合评估指数VIb为单位带宽下的准确性，VIb越大代表预测带的预测效果越好，计算式如式（9）。

基于综合评估指数确定模型参数的具体方法将在后文详细介绍。

三、二次指数平滑多期加权模型（QES-W）参数确定方法与结论

（一）样本数据的整理

本文选取2013年1月1日至2020年10月26日（不含节假日）全国生猪日均价为样本数据，根据杨雪和李文献基于调运指数研究对猪周期不同阶段划分的判断，将全样本数据分为两个子样本集（见图2）。

（二）衰减指数φ与预测期长l的确定方法

1比较多组初始预测值的预测效果确定最优衰减指数φ

令φ={080，085，090，095}，l∈{N+，且1≤l≤26}（N+表示正整数）， α=08代入式（1）—式（6）計算得到不同φ和l条件下的初始预测值，通过式（8）计算对应条件下的 VIa，结果如图3所示，图中26条曲线从上至下依次代表l取值为1到26时的评估结果。图中结果显示随着φ的增加，VIa逐渐减小，预测值的预测效果下降，且l越大，预测效果下降得越快。表明φ越小越好，因此确定最优衰减指数φ=08。

2比较多组初始预测值的预测效果确定预测期长l范围

根据上述结果令φ=08，令l∈{N+，且1≤l≤26}（N+表示正整数）， α=08代入式（1）—式（6）计算得到不同l条件下的初始预测值，通过式（8）计算对到应条件下的VIa，结果

如图4所示，图中结果显示应用不同周期的样本数据，预测值的预测效果均随着l的增大而下降，本轮周期下降得更为明显。对结果进一步分析，计算l每增加一个单位时VIa的变化百分比，结果如图5所示，图中结果显示上轮周期数据，随着l的增加，VIa变化率平稳下降;而本轮周期数据，随着l的增加，VIa变化率存在明显转折点，当l=19时，VIa变化率陡然增大，VIa恶化明显。以上结果表明l取值不宜超过18，因此确定l∈{N+，且1≤l≤18}。

（三）平滑系数α的确定方法

1应用定常系数方法确定平滑系数α

定常系数方法即在模型计算中使用固定的α，这种方法优点在于简单便于计算，缺点在于α无法适应所有阶段的序列变化，容易在某一阶段产生较大误差。应用定常系数方法确定α的步骤如下：

首先，令α=005m（m∈N+，且2≤m≤19），代入式（1）—式（6）计算初始预测值，通过式（8）计算VIa，产生18个（α，VIa）数据点;

其次，根据上述18个数据点，计算VIa关于α的回归方程：VIa=f（α）=aα2+bα+c;

最后，计算上述回归方程的一阶导数VI′a=f′（α）=2aα+b，令VI′a=0，即可得出对应最优α=-b2a。

结合（二）结果，令φ=08，l={N+，且1≤l≤18}，应用定常系数方法计算出的VIa关于α的回归方程和α的最优取值结果如表2所示。

2应用自适应动态系数方法确定平滑系数（α）

自适应动态系数方法是一种通过模型当前的预测误差来实时调整α的方法（盖春英和裴玉龙），其优点在于随着原始序列在不同时期的变化对α进行相应调整，以提高模型适当性，缺点在于这种调整是一种相对调整，并不是最优调整。应用自适应动态系数方法确定α的过程如式（10）—式（13）。

其中，αt表示t时刻的动态平滑系数，et表示t时刻的预测误差，Et表示t时刻的综合预测误差，Mt表示t时刻的综合绝对预测误差，Et和Mt分别是et和et的指数加权平均值，加权系数为γ，这里取γ=02（盖春英和裴玉龙）。

3比较两种方法下初始预测值的预测效果确定最优平滑系数（α）

应用配对样本t检验的方法比较两种方法下初始预测值的VIa，结果如表3所示，不同样本数据均显示使用定常系数确定的α最优取值的预测效果显著高于使用自适应动态系数，因此本文最终确定α的取值为定常系数。

（四）加权系数（β）的设计与确定

1应用全期加权方法计算加权预测值

全期加权方法是对当前时刻所有的初始预测值进行加权，这种方法的优点是包含更多的数据信息，缺点是不同时刻初始预测值的数量不同，加权系数需根据情况重新调整，计算较复杂。初始预测值与加权预测值关系见图6，使用全期加权方法时，t+1时刻的加权预测值是对l=1至l=18的18组初始预测值进行的加权，t+2时刻的加权预测值是对l=2至l=18的17组初始预测值进行的加权，为保证至少5个加权因子，仅计算至t+14时刻，即对l=14至l=18的5组初始预测值进行加权。

加权系数计算如式（14）所示。

其中，q为连续的两个初始预测值之间的比。

应用全期加权方法确定βi的步骤如下。

首先，令q=005m（m∈N+，且2≤m≤20），代入式（14）计算βi，将βi代入式（7）计算加权预测值，通过式（8）计算VIa，产生19个（q，VIa）数据点;

其次，根据上述19个数据点，计算VIa关于q的回归方程：VIa=f（q）=aq2+bq+c;

最后，计算上述回归方程的一阶导数VI′a=f′（q）=2aq+b，令VI′a=0，即可得出对应最优q=-b2a，进而根据式（14）计算对应βi。

结合前文计算结果，令φ=08，l={N+，且1≤l≤18}，α取值见表2，全期加权计算出的VIa关于q的回归方程及对应q最优取值结果如表4所示。

2应用移动加权方法计算加权预测值

移动加权方法是对当前时刻最近的5期初始预测值进行加权，相比于全期加权方法的优势在于计算简单，不用考虑加权系数的重新计算，缺点是损失了一部分的信息。使用移动加权方法时，t+1时刻的加权预测值是对l=1至l=5的5组初始预测值进行的加权，t+2时刻的加权预测值是对l=2至l=6的5组初始预测值进行的加权，依次类推计算至t+14时刻，即对l=14至l=18的5组初始预测值进行加权。加權系数计算如式（15）：

其中，i表示距离当前时刻的时间间隔。

应用移动加权方法确定βi的步骤与全期加权方法一致，结合（二）与（三）结果，令φ=08，l={N+，且1≤l≤18}，α取值见表2，移动加权计算出的VIa关于q的回归方程及对应q最优取值结果如表5所示。

3比较两种方法下加权预测值的预测效果确定最优加权系数（βi）

应用配对样本t检验的方法比较使用两种方法时多组加权预测值的VIa，结果如表6所示，不同周期样本数据显示全期加权方法预测效果不如初始预测值和移动加权，而移动加权计算出的加权预测值与初始预测值的比较在不同周期存在差异，上轮周期显示初始预测值效果更好，本轮周期显示移动加权效果更好，但两者之间的差值均很小。

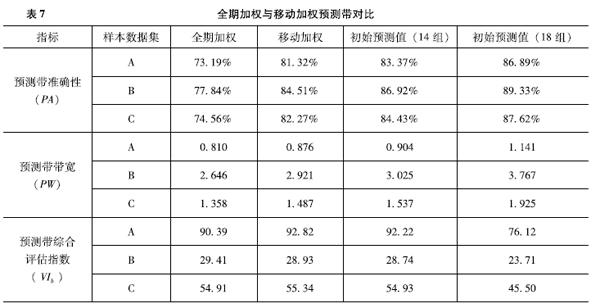
比较两种加权方法计算出的14组加权预测值构成的预测带、14组初始预测值构成的预测带和18组初始预测值构成的预测带的准确性（PA）及带宽（PW），根据式（9）计算VIb，结果如表7所示，不同周期样本均显示全期加权预测带的准确性不如移动加权和初始预测值，且PA<80%，移动加权预测带相比初始预测带准确性较低，但带宽有所减小，从VIb上看，移动加权预测带效果优于初始预测带。

综上所述，全期加权预测值和预测带的效果均不如移动加权，在预测值的预测效果上，移动加权与初始预测值差别不大，但在预测带综合评估上，移动加权优于初始预测值，因此最终选择移动加权。

四、本轮猪周期价格预测结果及评估

（一）模型验证样本数据

为验证模型对本轮猪周期生猪市场价格的预测效果，选取数据集B为样本数据（详见第三部分），将该章节确定的参数取值代入式（1）至式（7）计算。

（二）预测结果效果评估

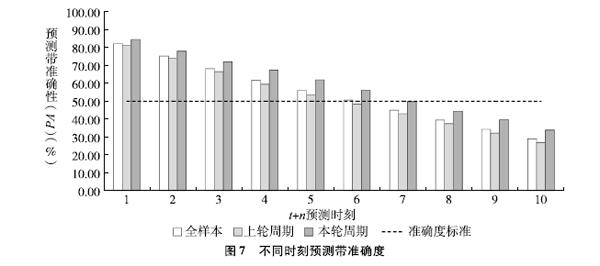
本模型对t+1时刻的预测具有14组加权预测值，t+2时刻具有13组加权预测值，依次类推，至t+14时刻仅有1组加权预测值，为保证多组加权预测构成的预测带具有一定的适应性，比较不同时刻的预测带准确性如图7所示，结果显示当预测时刻查过t+5之后，预测带的准确性逐渐低于50%，因此本模型最终仅呈现t+1至t+5共5组加权预测值，其效果评估如表8所示，拟合优度及预测误差的评估均达到良好标准。

五、总结

本模型使用的数据来源于卓创资讯，不同数据来源可能得到不同的预测结果，但只要原始数据统计标准一致就不影响模型趋势的预测。同时原始数据中不包含节假日数据，因此实际应用涉及节假日效应时需要结合其他模型和基本面信息进行调整。

在參数确定部分，主要对模型涉及的四项参数进行分解，在其余参数不变的条件下，逐一分析计算各个参数在模型总体达到最优效果下的取值。这种方法优势在于可以独立分析不同参数对模型的影响，且计算相对简单，一旦确定最优参数则可在模型整个运算过程中应用。但存在两个缺点，一方面未考虑不同参数间的交互作用，独立计算的最优取值，并不一定是使模型达到最优的参数组合;另一方面一旦确定参数后就不再进行调整，难以适应原始序列不同时期的变化规律。后续对参数的研究需要建立VIa关于φ、l、α、β的多元回归方程，动态输出当前时刻预测效果最优条件下的参数组合。

在预测效果评估部分，主要基于六项指标对模型进行静态评估，只能保证模型可用性，反映模型总体性能，无法保证一段时间内模型适当性始终保持良好状态，模型在实际应用中的稳定性需要通过模型的动态监控和校正来实现，这也是后续研究的重点。

对模型预测值的进一步分析有利于提高应用的准确性和精确度。首先基于对多组预测值的一致性评估分析最新预测值的可能偏离方向，提高预测准确性;然后基于对预测值与实际值差异，通过动态指标评估，分析价格变化规律;最后由于使用的数据频率不同，模型既可预测日均价，又可预测周均价、月均价等，预测短周期时精确度高，预测长周期时精度低但具有时间提前的优势。通过长周期预测值的提前性，可对短周期预测值设计控制线，进一步提高预测精确度。

通过本模型研究价格变化规律是对长周期量化模型的补充，综合不同模型对趋势判断的研究，通过长周期模型预测价格周期阶段，通过短周期模型判断阶段起点和终点，也是进一步研究的重点。

参考文献：

[1]冯金巧，杨兆升，张林，董升一种自适应指数平滑动态预测模型[J]吉林大学学报（工学版），2007（6）：1284-1287

[2]盖春英，裴玉龙自适应指数平滑模型预测区域经济研究[J]公路，2001（11）：43-46

[3]马丽娜探索基于指数平滑模型的农产品价格预测[J]农村经济与科技，2020，31（10）：336-337

[4]王玉明，孟蕾，李娟生指数平滑法在黑热病发病预测中的应用[J]地方病通报，2010，25（3）：24-25，29

[5]杨雪，李文献本轮猪周期主因非洲猪瘟量化模型设计及价格预测效果评估[J]中国猪业，2020，15（5）：26-32，38

[6]杨雪，李文献生猪调运指数设计与分析应用[J]今日养猪业，2021（1）：67-70

[7]付楠楠生猪期货的市场影响分析[J]中国证券期货，2020（3）：17-20

[8]BROWN，ROBERT GStatistical forecasting for inventory control[M]New York：McGraw/Hill，1959

[9]GARDNER E S，MCKENZIE A EForecasting trends in time series[J]Management Science，1985，31（10）：1237-1246

[10]HOLT C CForecasting seasonals and trends by exponentially weighted moving averages[J]International Journal of Forecasting，2004，20（1），5-10