聚焦小学数学教学核心素养实践探索

雷芳

一、教材分析

数学广角的目的是让学生接触数学思想方法，经历猜想、推理、验证等数学探索的过程，激发学生对数学的好奇心和求知欲。“鸡兔同笼”问题最早出现在大约1500多年前古代数学名著《孙子算经》中，是最具代表性数学问题。经调查，五六年级学生解答鸡兔同笼问题，仅少数学生会用假设法和方程法答题，却难以讲解思路。这不难看出他们只会套用做题的方法，并没有理解数学的本质。因此，数学教法和学法上应将有序思考与合适调整作为探讨的重点。

二、学情分析

“鸡兔同笼”问题对于四年级学生难以理解，四年级的学生虽具备应用逐一尝试法、列表法解决问题的能力，初步接触多种解题策略，但在数学的应用意识和应用能力有待提高。

三、教学目标

1.知识技能目标：通过探索学习、合作交流，让学生用不同的方法解决“鸡兔同笼”问题。从中渗透“化繁为简”的思想，掌握列表法、假设法等解决数学难题，尤其通过图示“数形结合”体验“假设法”。

2.情感态度目标：在解决问题过程中，培养学生的迁移思维能力，感受古代数学问题的趣味性。

3.教学重点：渗透化繁为简的思路，学会有序列表，适度调整列表法，体会假设法的逻辑性和一般性。

4.教学难点：理解用假设法解决“鸡兔同笼”问题的算理。

5.教学资源的开发和利用：“鸡兔同笼”历史资料显示，古人抬腿法的视频，教学课件简单有效，探究单的准备，学生课堂发表的观点由学生评价，产生质疑由学生讨论来解答，有效运用了“生成”。

四、教学过程

（一）创设情境

师：我们来读一下：

今有雉兔同笼，上有三十五头，

下有九十四足，问雉兔各几何？

师：朗朗上口胜似古诗。

师：这是1500多年前的数学名著《孙子算经》中一道有趣的鸡兔同笼问题，谁能用现代文描述一下？

（学生说完后，出示白话文，做文字对比）

师：是否想到刚发探究单？观察一下有什么不同？

师：为什么老师把数据改小？

生：为了容易理解。

师：说的好。化繁为简，思路不变，请大家看看探究单。

探究单

班级：_______  姓名：_______

笼子里有若干只鸡和兔。从上面数有8个头，从下面数有26只脚。鸡和兔各有几只？

（1）从上面数有8个头，写成文字式：________________________

从下面數有26只脚，写成文字式：________________________

（2）猜测：鸡有7只，兔有1只，对吗？为什么？把你猜测的过程填写到下表中。

我的方法是：

我的结论是：通过上表我得出鸡有（    ）只，兔有（    ）只。

我的发现是：__________________________________________。还有其它方法吗？

设计意图：让学生理解化繁为简，探究单设计上凸显数量关系，学生方便列表。

（二）新知探究

师：好，小组开始交流。（小组交流3分钟，教师选取几份作品）

作品展示汇报交流

师：小组讨论非常热烈，刚才老师在巡视过程中，选了几份作品，我们先来看这份作品。

（只讲解数量关系）

师：首先我们请同学说说他的做法。该同学有哪方面值得赞赏？比如，我赞赏他的勇气;又有哪些需要改进的？大家说说。

师：是否又觉得自己有进步，请修正自己的数量关系。

（出示数量关系图片）

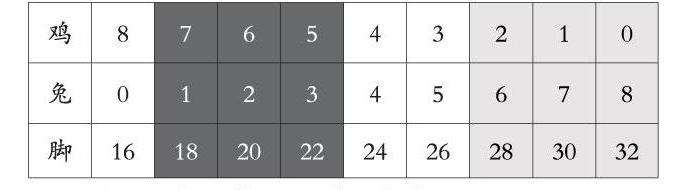
大家知道。数量关系作用非常强大，随便一组鸡和兔的数据，就能算腿是不是正确的？举例子，鸡7只，兔1只，总脚数是多少？显然不等于已知的26只脚，这猜测是不对的。我们利用数量关系来列表。

师：看表格，你们觉得怎样？好在哪里？

师：能发现出规律吗？是否有补充的？肯定学生答案，有序列举。每少一只鸡，每增加一只兔，多增加2只脚。刚才有同学采用多只调整，没有这几组数据，为什么呢？

（请学生讲）

师：任意一组数据开始，得到脚数比已知脚数少时，只要增加兔的只数，差值大调整的数据就多，明显能更快得出答案。反之，比已知脚多时，我们只要减少兔子的只数，即可。

（列表更简洁明了）

小结：其实列表法的用途非常广，三年级时租船问题也用列表法解决的，遇到题目不知如何入手时，可以通过这样有序列表，找到规律，适当调整是很好的思路。

设计意图：通过学生讲解，不难发现有序列表的规律，从而引导出适当调整数据——列表法。

师：还有其它方法吗？列表法确实是种好方法，刚才有的同学还用其它方法来解答，请大家看看（学生讲解）。

师：大家都听懂了吗？

（画图请学生上台边写算式边讲）

生：假设全部是鸡。

2×8=16只脚

我们来判断一下，这个假设对不对？显然不对，已知脚是26只，少了几只脚？

生：26-16=10只。

师：为什么会少了10只脚？

生：因为把兔子当成了鸡，为什么要除以（4-2）呢？一只兔子就少了2只脚，少的这10只脚是把几只兔子当成了鸡？（画）

10÷（4-2）=5只兔

8-5=3只鸡

假设全部是兔。

一共有4×8=32只脚，这个假设对吗？

不对，比已知腿多出了32-26=6只脚。

师：为什么会多出了6只脚？

生：因为把鸡当成了兔子，为什么要除以（4-2）呢？每只鸡多算了2只脚，那么多出的6只脚，就是把3只鸡当成了兔子。

6÷（4-2）=3只鸡

8-3=5只兔

师：大家觉得他讲得如何？请给予评价。

小结：刚刚我们学习了假设法，都是先假设脚全是鸡或全是兔做出判断，根据差的脚数做出调整，找到答案。

设计意图：学生通过画图分析，对假设法的理解能深入到本质。

请大家试着用上面的方法解决前面的“鸡兔同笼”问题。

（三）全课小结

师：古代是用什么方法来解决鸡兔同笼问题的呢？（视频）古人所用的抬腿法，其实也是假设法，可见古人的解题思路是多么巧妙，通过学习大家对不同的解题方法有更深层认识。

设计意图：了解古人的解题思路，开阔学生的思维。

板书设计（有序列表，适当调整）

笼子里有若干只鸡和兔。从上面数有8个头，从下面数有26只脚。鸡和兔各有几只？

假设法：笼子里都是鸡。

8×2=16只脚;26-16=10只脚;  4-2=2只脚;10÷2=5只兔 。

假设都是兔子，8×4=32 只脚。

32-26=6 只脚;6÷（4-2）=3 只鸡;8-3=5 只兔。

五、教学反思

本课是学生的课堂，学生互动评价，教师适当点评。

优点1：从数学本质上思考有序列表和适当调整，任何一组数据，都能通过脚总数的比较，有效调整鸡或兔的只数，且可以快捷得到最终答案，颠覆传统的有序列表方法。

优点2：用假设法的时，学生通过画图，来理解假设法，并理解为什么要4-2=2条脚，这是难点。学生互动讲评能轻松理解。

优点3：探究单设计得当，理解了数量关系，为课堂活动开展奠定基础，学生全程参与探索。

责任编辑  林百达