Diagnostics of a microhollow cathode discharge at atmospheric pressure

Chen ZHOU(周晨),Yueying LI(李玥颖),Zhi YU(俞鸷),Jingfeng YAO(姚静锋),Chengxun YUAN(袁承勋),2,∗and Zhongxiang ZHOU(周忠祥),2,∗

1 School of Physics,Harbin Institute of Technology,Harbin 150001,People’s Republic of China

2 Heilongjiang Provincial Key Laboratory of Plasma Physics and Application Technology,Harbin 150001,People’s Republic of China

Abstract Based on a sandwich-like structure,a microhollow cathode discharge device is designed,and a stable discharge is realized by injecting helium into the discharge region of the device at atmospheric pressure.A wall probe is used to determine the relevant parameters of the plasma generated by the device,such as particle density,electron temperature,and the electron distribution function.At the same time,a sink parameter is used to correct the electron distribution function of the wall-probe diagnostics,and to further study the relationship between electron density and the electron temperature of the corrected electron distribution function.

Keywords:wall-probe diagnostics,sink parameter,particle density,electron temperature,atmospheric pressure

1.Introduction

High-pressure discharge plasma has significant applications in industry[1–3].Plasma generated at atmospheric pressure is also important.It can have a high density and a small spatial range,making it useful for the precise surface treatment of materials[4–6].For example,such plasmas can reduce costs and improve efficiency in chip manufacturing.At present,dielectric barrier discharge plasma[7–9]and jet discharge plasma[10–12]are commonly used in atmospheric-pressure discharges.However,microdischarge devices[13–15]can not only produce stable plasma at atmospheric pressure,but also generate high current and a high deposition effect,making microdischarge plasma an attractive research topic.

Since it was originally proposed by Langmuir,probe diagnostic technology has been steadily developing[16,17].However,many problems still exist and need to be addressed.For example,the technique is hard to apply to the diagnosis of high-pressure and high-density plasma.At present,probe diagnostic theory is based on the collisionless model at low pressure,and is rarely used at high pressure,where the accuracy is not as good as for the collisionless model at low pressure[18,19].

Demidov et al[20]proposed a sandwich-like structure for an electrode[21],creating a microdischarge of a helium/air mixture at atmospheric pressure.Although the plasma electron spectroscopy generated by such a device at atmospheric pressure has been diagnosed many times,the diagnostic results are still less satisfactory than those obtained at low pressure[22].The current theories for probe diagnostics at high pressure have been summarized by Demidov et al.Also,a sink parameter has been used to correct the results of probe diagnostics,and the advantages of wall-probe plasma diagnostics at high pressure have been proposed[23,24].However,the theory has rarely been verified experimentally.

In this paper,we report the design of a discharge device with a microhollow cathode.When the device is used to inject an appropriate amount of helium at atmospheric pressure,a stable discharge is realized.The traditional Langmuir method is used to analyze the plasma density,and the ion density at the saturated ion current is also characterized.Based on the Bohm criterion,we analyze the trend of change of the electron temperature with current.At the same time,the assumptions of Maxwellian and non-Maxwellian distributions are fitted to the electron energy distribution function(EEDF).Also,the dependence of electron temperature and electron density on current,obtained using different fitting methods,is further studied and analyzed.Finally,a sink parameter is used to correct the electron distribution function(EDF),and the dependence of the corrected electron temperature and electron density on current is studied.

2.Experimental setup and theory

2.1.Experimental setup

For probe diagnostics at atmospheric pressure,a stable and diagnosable plasma source is essential.A microdischarge device has therefore been designed,consisting of three sheets of molybdenum and two sheets of ceramic(Al2O3),each 0.15 mm thick.The molybdenum sheets serve as the anode,cathode,and wall probe,and the ceramic acts as an insulator,as shown in figure 1(a).The helium is injected into the hole in the middle.Recently,some researchers have suggested that a steady discharge at atmospheric pressure requires an electrode hole diameter less than 0.2 mm[22].For that reason,a hole with diameter of 0.12 mm was punched by a femtosecond laser(figure 1(b)).Figure 1(c)is an image of the microdischarge device,in which the bright region in the middle is the discharge region.

Figure 1.(a)A schematic of the discharge device,(b)a picture of the experimental device and(c)an image of the discharge.

Figure 2 is a block diagram of the experimental setup.A 0–1500 V adjustable DC power supply is chosen,with a 100 kΩ resistance to protect the circuit.Note that the voltage and current can be read directly from the power supply.The helium is controlled by a fine-tuning valve.For data acquisition,a Langmuir single probe system is used,with a voltage range of–150 V to +150 V;the scan step size is 0.2 V.Specifically,the typical parameters are a voltage of 450 V and a discharge current of 6.6 mA.

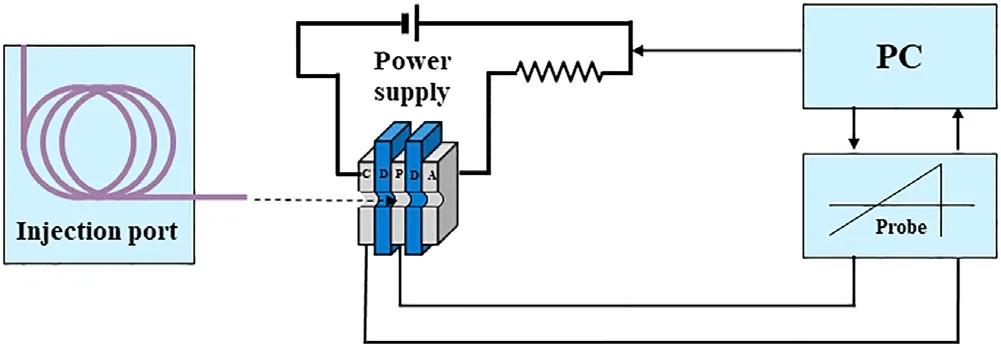
Figure 2.Block diagram of the experimental setup.

Since the wall probe and the discharge electrode are the same size,it is inevitable that the electric field and discharge between the cathode and the anode are affected by the wall probe.By comparison with the typical I–V characteristics of a Langmuir probe used to diagnose plasma,it is found that the difference between the typical[25]and experimental(figure 3)characteristics is not large,so the diagnostic result of the wall probe reported here is reliable.

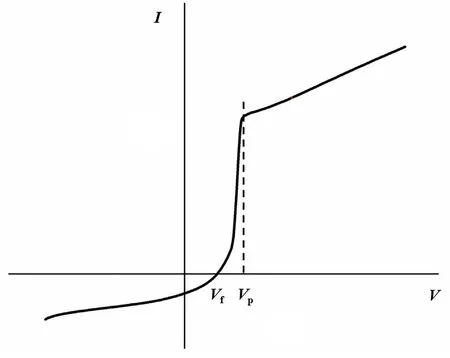
Figure 3.The I–V characteristics of a wall probe.

Figure 4 shows the I–V characteristic of the microdischarge device for different probe diameters.It can be seen that when the output current is in the range of 2–15 mA,there is an increasing voltage–current characteristic.Therefore,the discharge is in the abnormal glow discharge region[25].The floating potential is then small,which is conducive to probe diagnostics.Since the probe’s diagnostic range is–150 V to+150 V,this area cannot be diagnosed with the existing probe system.In this experiment,the discharge current is chosen to be in the abnormal glow discharge range of 2–15 mA.Another reason for choosing a small discharge current is that as the current increases,the corrosion of the device increases.

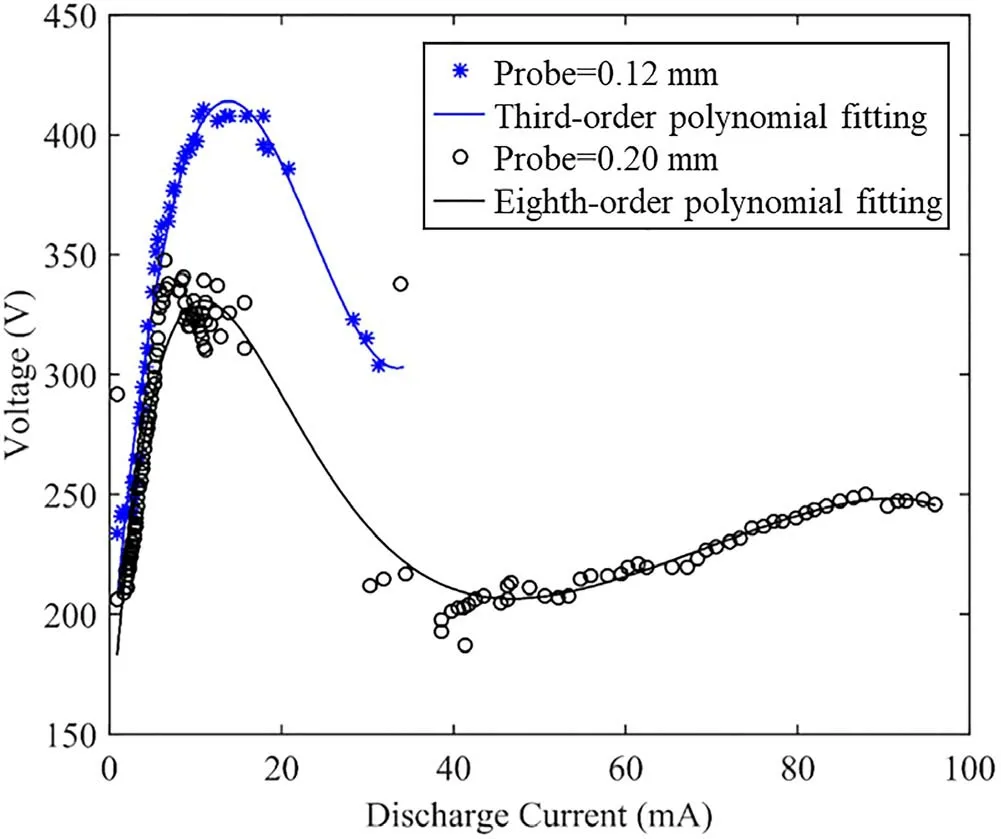
Figure 4.The I–V characteristic of microdischarge devices with different probe diameters.

2.2.High-pressure probe diagnostic theory

In recent years,the theory of probe diagnostics at atmospheric pressure has made great progress.At high pressure,the probe can act as a sink for nearby electrons.This produces a reduction of the electron density near the probe,arising from electron absorption(recombination)on the probe’s surface.A distortion of the EDF is caused by the limitation of the diffusion replenishment rate of the depleted electron region flowing into the probe.This reduces the detector current at any energy.This being the case,a correction term should be added to the electron energy[23]:

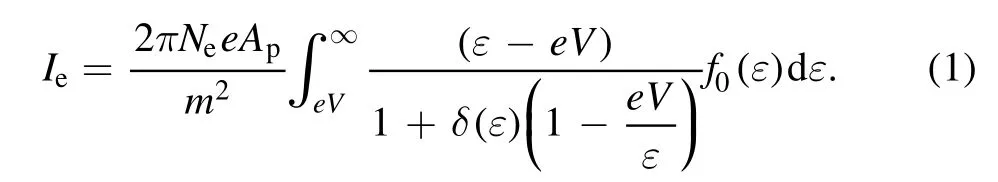
Here,Neis the electron density,Apis the probe area,andδ(ε)is the sink parameter,which is an artificially defined quantity related to the electron energy.For different probe structures,the following relations are satisfied:

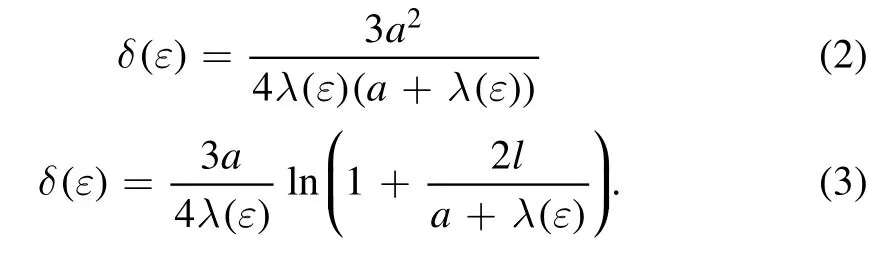
In these equations,which represent the sink parameter of the spherical probe in equation(2)(see figure 5(a))[26]and a cylindrical probe in equation(3)(see figure 5(b))[23],a is the radius of the circular and cylindrical probes,l is the length of the cylindrical probe,andλ(ε)is the mean free path of the electrons.As opposed to a collisionless mean free path,the energy-dependent mean free path represents the displacement that occurs when the electron loses 1% of its energy.When the probe size is large enough(a/λ≫1[27]),the following relationship is satisfied[23]:

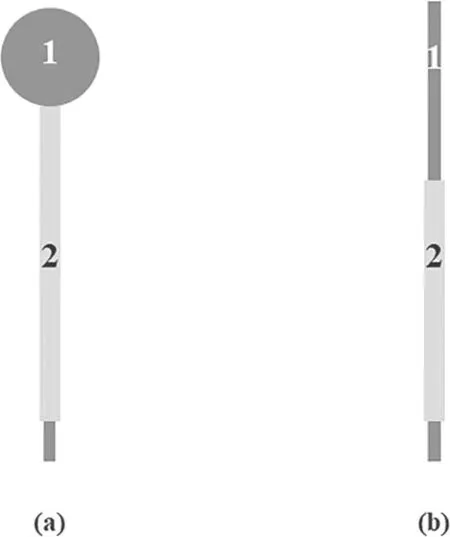
Figure 5.Typical probe constructions:(a)spherical and(b)cylindrical probes.1 designates a conductor and 2 an insulator.

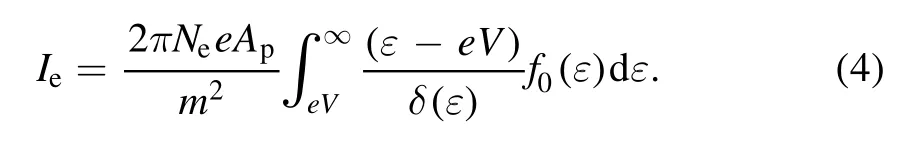
From this relationship,Demidov obtained the electron distribution function,which is proportional to the first derivative of the current with respect to the voltage:

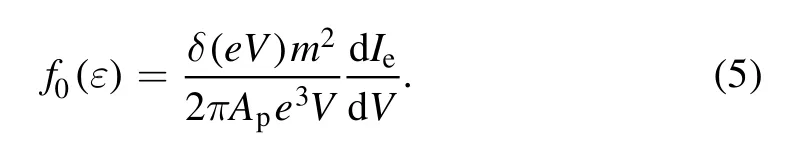
This parameter definition is consistent with the definition of the Druyvesteyn formula[28],which is the theoretical formula governing the EDF in a plasma with collisions.If the size of the wall probe used in this experiment is sufficiently large,it is feasible to use the above simplified formula.The main problem is then to find an accurate sink parameter.In this paper,the electron mean free path and the diameter of the probe are assumed to be nearly the same,

which can be substituted into equation(3).Therefore,

So,the sink parameter is assumed to be 1.

3.Results and discussion

3.1.Plasma parameters

3.1.1.Particle density obtained by the Langmuir/ion saturation current method.Electron density is obviously an important plasma parameter.The same is true for the electron temperature,which provides a means of understanding the plasma heating mechanism.This experiment therefore first uses a traditional diagnostic method to obtain the electron density and effective electron temperature.

Traditional probe theory can diagnose some plasma EEDFs at low pressure,and the calculation of electron density by saturation current is also readily achieved in this experiment.According to the Bohm criterion,the energy obtained by ion acceleration in the pre-sheath is equal to half of the electron temperature,making it possible to obtain the density at the boundary between the pre-sheath and the sheath.Further,the density in the plasma region can be obtained by assuming a Boltzmann distribution of electrons.

Here,neis the electron density in the plasma region,nsis the electron density at the boundary between the pre-sheath and the sheath,Isatis the saturated ion current,M is the ion mass,andkTeis the electron temperature.Although there is a loss of ions in the sheath,in this paper,we assume that the ion flux at the boundary is the same as at the probe wall,and that the ions are accelerated in the sheath to satisfy the condition of constant flux.The electron current at the plasma potential(which is small due to the electron sink effect)is related to the saturated ion current:

This electron current formula can be used for high-pressure collision plasma diagnostics.Here,Vpis the plasma potential(probe potential)andis the current at the plasma potential.

Figure 6(a)shows the variation of electron density obtained by the Langmuir method.The plasma density obtained in this way is 1000 times smaller than it is at atmospheric pressure.Due to the density change caused by the difference in electric field,the electron motion is no longer simple collisionless particle motion at high pressure,but is effectively a fluid motion with collisions.Under the effect of the probe’s potential field,it is appropriate to describe the electron flow as diffusion.Under the influence of gas flow velocity,the discharge pressure is less than atmospheric pressure,so the density is less than the theoretical value of atmospheric-pressure discharge density.In addition,this experiment diagnoses the electron density in the glow region,where it is reasonable that the density is smaller than that in the positive column region.With increasing current,the density increases.In this experiment,the influence of gas flow velocity on the diagnostic results is also considered,so the diagnostic operation is repeated at half of the abovementioned experimental gas flow velocity.

The Langmuir method can show the trend of variation of plasma parameters.The density is larger at high pressure,as expected.Although the diagnosis is made in an open environment,due to the existence of the airflow at the probe position,the actual pressure should decrease as the gas flow velocity increases.This provides a very effective method for predicting the plasma density from the gas pressure and plasma temperature.

However,the probe diagnostic of plasma with ion saturation current for calculating plasma density is as broadly applicable as the Bohm criterion method.It can be seen from figure 6(b)that the ion density obtained by this diagnostic method is closer to the true plasma density than that obtained by the Langmuir method.The calculation of plasma density by ion saturation current only needs to satisfy the conservation of flux in the sheath,whereas the Langmuir method needs to satisfy the collisionless assumption in the sheath[25].In a collisional plasma,this assumption is obviously not applicable,and the diffusion expression for electron motion is more useful.Compared with the main electron group,fast electrons better satisfy the collisionless assumption.Therefore,fast electrons constitute an important part of the saturation current.Since the airflow is relatively low,the gas pressure is higher.Hence,the fast electron motion is limited,which leads to an increase of current,while the electron density obtained by the Langmuir method tends to be smooth.The fast electron group is more suitable than the main electron group for the collisionless assumption.

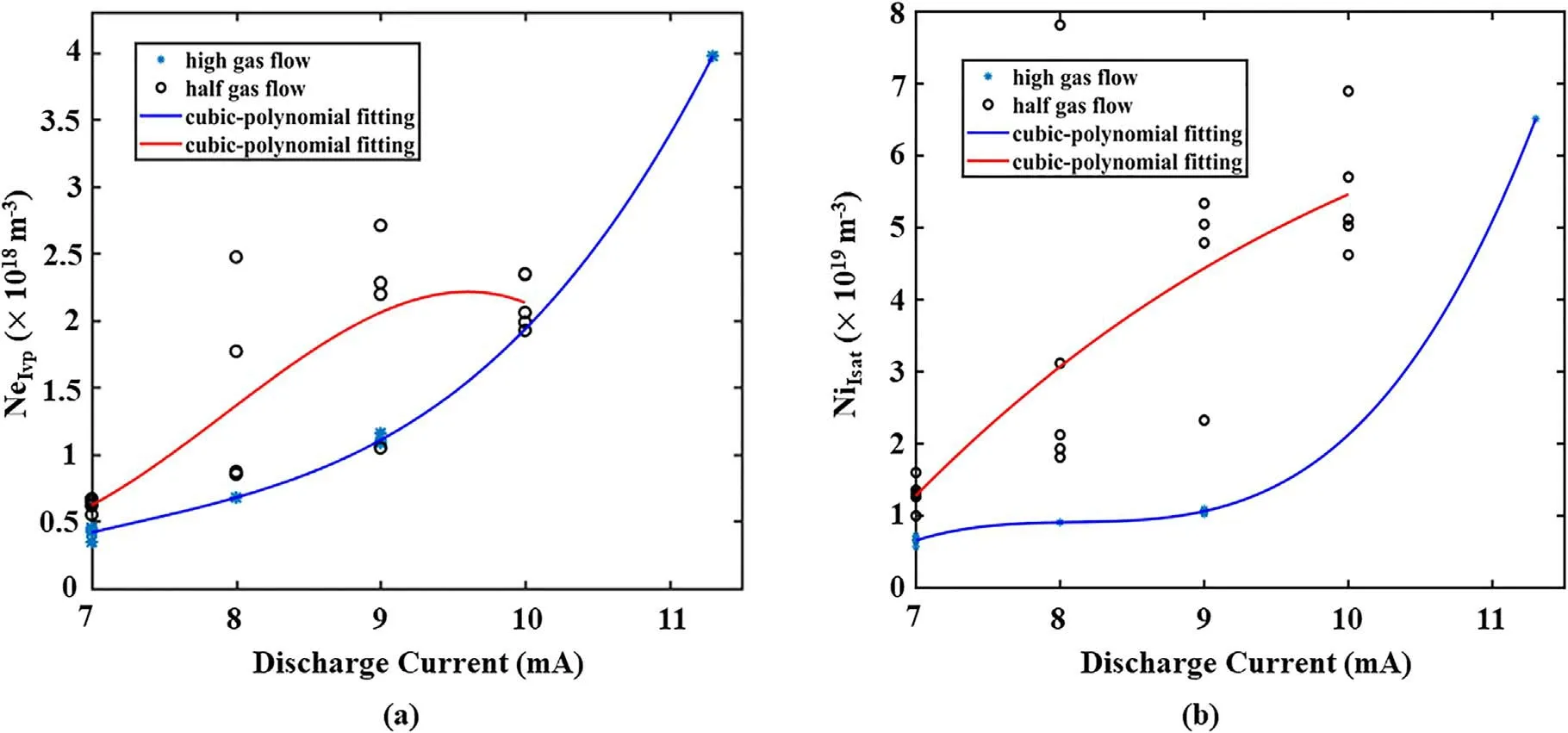
Figure 6.(a)Electron density obtained from the current at the plasma potential.(b)Ion density obtained from saturated ion current.

3.1.2.Electron temperature obtained by the Bohm criterion method.As is well known,stable discharge is the prerequisite for obtaining accurate probe diagnostic parameters.It can be seen from figure 7 that stable diagnostic parameters can easily be obtained using a higher gas flow velocity,reflecting the fact that the microdischarge device is more stable at low pressure than at high pressure.According to figure 6(b),the operating current of the device can reach more than 10 mA at low pressure,while at high pressure a stable discharge is only maintained between 6 mA and 10 mA,even though the breakdown voltage of the device is relatively high.Therefore,to obtain plasma parameters at high pressure,an appropriate pressure range needs to be provided.It is worth noting that the parameters obtained for higher current are more stable at high pressure,which is related to the structure of the wall probe.Because it is difficult to generate a stable plasma glow discharge region at low current,once voltage is applied to the wall probe,the discharge conditions of the entire device are changed.Eventually,there will be a discharge between the probe and the cathode,which is not conducive to accurate I–V characteristic diagnostics and the determination of the plasma potential and EDF.However,if the plasma is nonlocal(the energy relaxation length of the electron is equal to or greater than the plasma dimensions)and the electron temperature is low(the self-consistent field of the plasma is low,～0),then the fast(highly energetic)part of the EEDF can be measured without distortion.Our group has reported on this problem[29].In addition,a series of papers has also reported on this problem[15,20,22].According to the literature[29],the plasma generated by the device is non-local and the electron temperature is low.So,it is feasible to diagnose plasma with a wall probe.

Figure 7.Electron temperature obtained by the Bohm criterion at high and low gas flows.

Because the probe produces both a sheath and a presheath in the plasma,the Bohm criterion can be used to obtain the electron temperature rather accurately:

Here,Vfis the float potential.This diagnostic method is used in traditional probe diagnostics,and currently matches the diagnostic at high pressure to a high degree.It can be used to predict plasma density parameters.

As shown in figure 7,the electron temperature tends to be stable as the gas flow velocity increases,which further reflects the stability of the plasma.

In addition,the plasma temperature at low pressure is significantly higher than that at high pressure.It can be concluded that the plasma at high pressure reduces the electron temperature to maintain the gas discharge state.This is consistent with the tendency of electron density and electron temperature in low-pressure discharge plasma to change as current changes.In addition,different trends of plasma parameters with current under different pressures are caused by the non-locality and locality of fast electrons in the plasma.The increase of electron density in a non-local plasma is maintained by a decrease of electron temperature,which,in a plasma,is a heat dissipation phenomenon.Nevertheless,plasma at high pressure has the properties of a localized plasma,and its electron temperature tends to be stable as the electron density increases.Under these conditions,the electrons in the plasma are in a state of thermal equilibrium.

3.1.3.Electron density and electron temperature obtained by the distribution function.Figure 8(a)shows the calculated electron density obtained by fitting the energy integral of the EEDF.It can be compared with the electron density obtained at the plasma potential.Both show the same density value and the same trend of density change.However,the EEDF obtained by fitting only shows the distribution characteristics of the main fraction of the electrons,because the EDF is obtained under the assumption that the sheath is collisionless.At the same time,it also confirms that the EDF obtained using the second derivative has a relatively large error.In the published literature[19,23],it is pointed out that the EDF obtained using the second derivative under high pressure is smaller than the EDF obtained using the low pressure collisionless model.This is because it is difficult to satisfy the collisionless assumption when the electrons in the sheath move to the probe’s surface.The introduction of the sink parameter can effectively correct this problem.

Assuming a Maxwellian distribution,the experimentally obtained EDF is fitted to obtain the electron temperature.Interestingly,the electron temperature obtained by this method is similar to that obtained by the Bohm method.It can be seen from figure 8(b)that the electron temperature decreases with increasing current.Unlike what is found using the Bohm method,the electron temperature at low pressure is less than that at high pressure,but the electron temperatures obtained by the two methods are very consistent at high pressure.The Bohm method is more general,and the function fitted with the single-temperature Maxwellian distribution only reflects the electron temperature of the main electron group;it does not include the temperature of the higherenergy,faster electrons.

Many electron distribution functions do not completely satisfy the ideal Maxwellian distribution,but some are still close to it,and the two-temperature Maxwellian distribution is commonly used.The electron temperature obtained by the above-mentioned fitting method only shows the temperature of the low-temperature electron group,ignoring the temperature of the high-temperature electron group.In particular,the EDF in the helium discharge plasma will also have electron groups of higher energy.This is a characteristic of metastable helium atoms and an important phenomenon in plasma collisions.The EDF can generally be divided into three parts.The first part,the electron group with lower energy,shows the characteristics of a Maxwellian distribution,with a lower electron temperature,generally less than 1 eV.The second part is the hightemperature Maxwellian distribution formed by the higher temperature electron group,for which the temperature is about 10 eV.There are also some electrons(the third part)that do not conform to the Maxwellian distribution.A large number of electrons with specific energy are reflected in the EDF because of the large number of collisions in the plasma.Therefore,the electron density and effective electron temperature are obtained by the direct interpolation of the second derivative,and they are more in line with the real state of the plasma.

Figure 9(a)is a graph of electron density versus current based on a non-Maxwellian distribution.The trend of electron density obtained by this method is consistent with that obtained by fitting to a Maxwellian distribution,but the trend obtained by fitting to a non-Maxwellian distribution is more obvious.Also,the repeatability is better than that of the method of obtaining the plasma density using the current at the plasma potential.Unlike the electron density parameters obtained by Maxwellian distribution fitting,the electron density obtained by this method does not only show the distribution characteristics of the main electron group,but also shows the distribution of the fast electron group at higher energies.

A common strategy is to obtain the EEDF from the EDF.Using the EEDF to obtain the electron density and the average energy of the electrons is an important method for describing the plasma.Therefore,it is very important to have a way of obtaining an accurate EDF.An accurate EDF can yield accurate plasma parameters,but the EDF reflected by the parameters may be inaccurate.The EDF obtained by different fitting methods followed by the diagnosed plasma density can therefore only be used as a reference for judging the accuracy of EDF.Another method used to study the EDF is the collision electron energy spectrum.Under suitable discharge conditions,the EDF inferred by this method can accurately reflect fast electron peaks.

Figure 9(b)shows the effective electron temperature obtained by the EDF under the assumption of a non-Maxwellian distribution.The trend of the effective electron temperature obtained under non-Maxwellian distribution conditions is consistent with the electron temperature obtained by the Bohm method,and both show the experimental phenomena of high airflow and high electron temperature.Unlike the case in which a Maxwellian distribution is assumed,the effective electron temperature reflects the average energy of all electron groups,not the temperature of just the low-temperature electron group.The results show that the changing trends of the average electron energy for the two pressures are complementary.The average energy of the electrons in the low-pressure discharge plasma first increases steadily and then shows a downward trend.The electron temperature under the assumption of a non-Maxwellian distribution is consistent with the trend of electron temperature change obtained by the Bohm method,but the temperature is greater.This is because the electrons experience collisions in making their way to the probe,which introduces an error into the EDF diagnosed under the assumption of a non-Maxwellian distribution.In turn,the electron energy value is large,and the peak position shifts to a higher energy.This is consistent with the subsequent diagnostics of the EDF.Therefore,under high pressure,the second-derivative diagnostic EDF only describes the electron distribution accurately in the high-energy range.In the resulting collision electron energy spectrum,the second derivative can still be used to express the high-energy fast electron group.

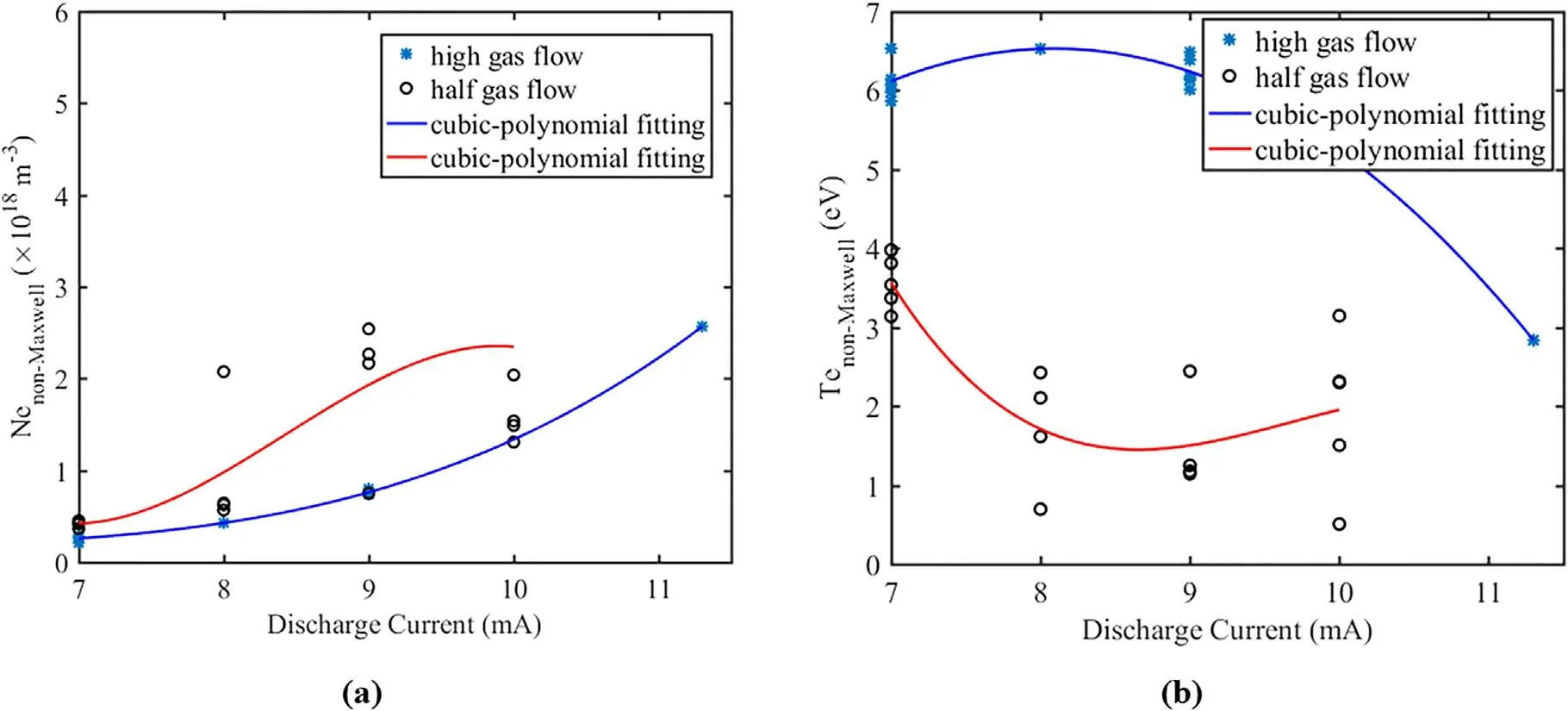
Figure 9.(a)Electron density and(b)electron temperature obtained by the assumption of a non-Maxwellian distribution.

3.2.EDF corrected by the sink parameter

Figure 10(a)shows the diagnostics of the EDF at different pressures.The results show that changing the current has little effect on temperature.Low current corresponds to lower plasma density.

Combining the previous results,it can be concluded that low-pressure plasma has a characteristic resembling a twotemperature distribution,while high-pressure discharge plasma is closer to a Maxwellian single-temperature distribution.In other words,the distribution of electrons at low pressures is more uniform,but in fact,fast electrons are hidden in the distribution.Figure 10(a)shows that there is a small characteristic fast electron peak at 20 eV,which is the characteristic metastable helium atom peak.However,at low pressure,the EDF is subject to the influence of noise,and can only delineate the fast electron distribution below 10 eV.Because of the characteristics of the two-temperature distribution,there is also the problem that fast electrons are concealed in the high-temperature electron group.This means that the effect of the sink of electrons is to cause the EDF obtained by the second derivative to have a larger error.

Figure 10(b)shows that the electron distribution function has the same properties as the EDF obtained by the secondderivative method.Low pressure produces a two-temperature distribution,and high pressure is approximated by a Maxwellian distribution.However,it is difficult to distinguish the characteristic electrons of metastable helium atoms.

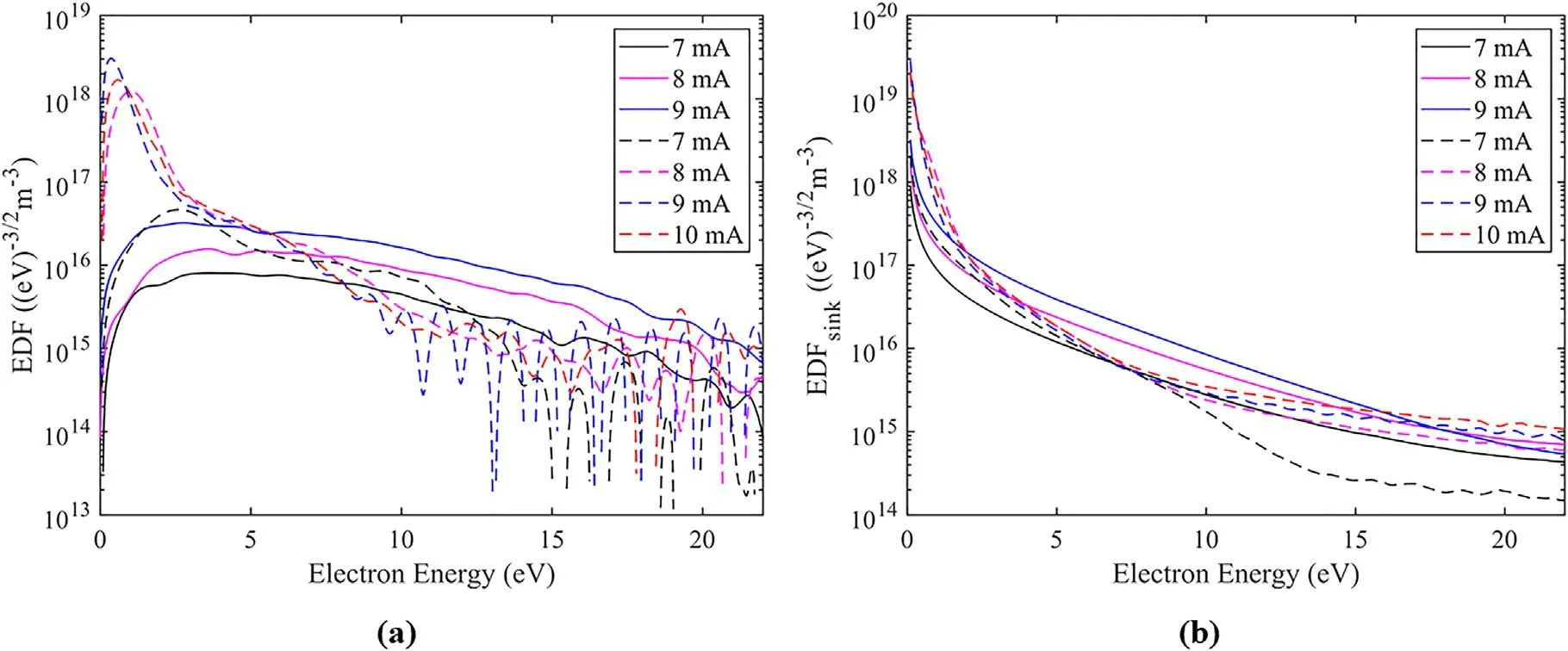
Figure 10.(a)The EDF obtained by the second derivative and(b)the EDF obtained using the sink parameter correction.The dotted lines represent low pressure and the solid lines represent high pressure.

In this experiment,since the wall probe is much larger than the electron energy mean free path,one might think that the sink parameter should be much larger than 1.However,the sink parameter is related not only to the probe size,but also to the mean free path of the plasma electron energy.For non-local plasma,the mean free path of the electrons is relatively large,roughly the size of the whole device.Unfortunately,this experiment does not satisfy the non-local plasma conditions under such discharge conditions.Correspondingly,it is difficult to observe the characteristic peak of the metastable helium atom in the EDF,which makes it difficult to obtain accurate results when the sink parameter is set to 1.Theoretically,an effective sink parameter can compensate for such an error.

The EDF obtained by the first derivative is smoother and has less noise than the EDF obtained from the second derivative.To obtain a more accurate EDF,more sensitive electrical detection methods are needed.The acquisition interval of the I–V characteristic acquisition instrument is only 0.2 V.From the second-derivative result of the I–V characteristic,this method has difficulty distinguishing between high-energy electrons and high noise levels.This is because the acquisition system is only a simple microcomputer that controls the output voltage and detection current;the means of detection need to be improved.

Figure 11(a)shows the electron density obtained using the EDF,taking account of the effect of the electron sink due to the probe,which is consistent with the EDF obtained by the second derivative.

Figure 11(b)shows the electron temperature obtained by EEDF integration,which is consistent with the electron temperature obtained by the second derivative.

Figure 11.(a)Electron density and(b)electron temperature obtained by the EDF with sink parameter correction.

4.Conclusions

This paper reports the design and testing of a microhollow cathode discharge device.A stable discharge is achieved by injecting an appropriate amount of helium into the atmospheric environment,and a probe diagnostic is realized at high pressure.At the same time,a wall probe is used to diagnose the plasma and to provide experimental results.This paper also compares our results with plasma parameters obtained by present-day high-pressure diagnostic theory and with results obtained by the collisionless model probe diagnostic method.The results show that the plasma parameters corrected by the sink parameter are better than those obtained by collisionless theory.Interestingly,the method of obtaining the electron temperature through the Bohm criterion is found to be applicable to both high-and lowpressure conditions,and can provide a reference value for subsequent fast electron analyses[30–32].

Acknowledgments

The research has been financially supported by National Natural Science Foundation of China(No.11775062).