机动管线充气排液过程中油-气体两相流阻力特性

姜俊泽，张镇，李江，陈雁，陈明，蒋苇

(1.陆军勤务学院 油料系，重庆 401311；2.耐德工业股份有限公司，重庆 401300；3.综合训练机构，北京 102218)

0 引言

机动管线是油料保障的骨干装备，管线撤收前需要对管内油料进行排空回收。采用压缩空气进行管线排空具有不受环境条件影响、不需要水源、不需要进行油水分离等优点，是高原高寒和水资源缺乏地区排空管线的不二选择，而准确预测排空过程的阻力特性是进行管线排空工艺设计的基础。

管线充气排空过程与输油管道的清管有一些相似之处。关于管道清管过程的相关研究较多，而针对机动管线充气排液过程的研究较少。Baker[1]很早就开始清管现象研究，基于实验数据和现象观测，提出一个理想的清管模型，将管道分成未扰动多相流区、液塞区、干气区和多相流再生区，并利用稳态方程计算管流的阻力。Minami[2]在Baker模型基础上进行了瞬态清管的实验和理论研究，将管道分为管线上游区、清管液塞区和管线下游区3个流动区域，并且模拟清管及清管后整条管道流体的流动，同时对清管模型及瞬变流模型进行耦合。后来一些学者也基于上述模型建立了清管模型，如Lima等[3]、Nguyen等[4]、史培玉等[5]，但也都是针对使用清管球的清管过程。由于成品油的强挥发性，清管过程中的气体与液体(简称气液)两相流动伴随有剧烈的相变和传质现象，并且管内油品不断减少，气体不断增加，管内的阻力变化表现出明显的非线性特征，这与其他条件下的两相流动和单相流动存在显著区别。油-气体两相流的发展和管内油品数量变化直接影响着管流的阻力特性。

许多研究者试图用一种模型来预测所有流动模式范围内的两相摩擦压降。模型通常分为均质流动模型(HFM)和分离流动模型(SFM)。HFM假设两相在流动过程中充分混合并且以相同的速度流动而没有任何界面滑移，而SFM则认为两相分别以不同的速度流动但在它们之间共享界面，并且气相和液相的运动分别遵循其自身的解析解[6]。

一些研究人员对垂直管和向下管的两相流动摩擦压降进行了研究。Yao等[7-8]在室温下进行了实验，实验的出口压力在0.17～ 0.28 MPa范围内，随着管路内径的增加，现有的垂直向下管内气水两相流摩擦压降相关性的预测精度显着降低。另一些研究者对制冷剂在微型管中沸腾所引起的压降进行了理论和实验研究，并建立了两相流的相关性模型。由于微型管的直径只有1～4 mm，液体表面张力对压降影响较大，对摩擦力影响较小[9-11]。因此，这些结论仅适用于微型管和低压状态，不适用于大直径的管路。Ribatski等[12]在913个实验数据中比较了12种两相摩擦压降的关系式，其中8种流体在微尺度通道中流动，质量流量在23～6 000 kg/m2·s的范围内，结果表明这些关系式的通用性均较差，即使是最准确的关系式也只能在30%的范围内有较高的精度。Zhang等[13]对典型的中国喷气式飞机燃料RP-3流经绝热水平微型管的流动阻力特性进行了实验研究，其压力范围为1～2.58 MPa，实验温度为295～789 K，质量流量达1 573 kg/m2·s.实验结果表明：当降低的温度小于0.95%时，摩擦阻力在相同质量通量下的多种压力下相等；当降低的温度大于0.95%时，摩擦阻力不相等，也就是说温度变化对阻力有一定影响。Zhang等[13]还根据实验数据提出一个新的摩擦系数关系式，来提高经典模型的适用性。Zhu等[14]也在压力范围3～6 MPa、温度329～810 K和质量通量803.71～1 607.4 kg/(m2·s)的条件下进行了相似的研究。结果表明，摩擦系数随着温度的升高而上升，在准临界点达到峰值，然后逐渐下降至稳定值，据此提出了一种新的摩擦系数关系式，其平均偏差为5.1%，其中90.3%的数据点在±10%误差带内。

由于机动管线充气排液过程中油品不断减少，系统阻力呈现非线性变化，之前的研究成果不能有效解决这一过程的阻力预测。本文针对机动管线充气排液过程特点，建立管线气液两相流阻力计算模型，用于分析和预测排空过程系统阻力的动态变化特性，为机动管线工艺设计提供理论依据。

1 充气排液过程流动阻力的计算模型

充气排空过程管内的流动体可分为3部分，一部分是单相气体段，一部分是气液混合段，一部分是单相液体段，如图1所示。由于气体段压力损失较小，本文建立的模型主要考虑气液混合段和单相液体段的流动阻力计算问题。

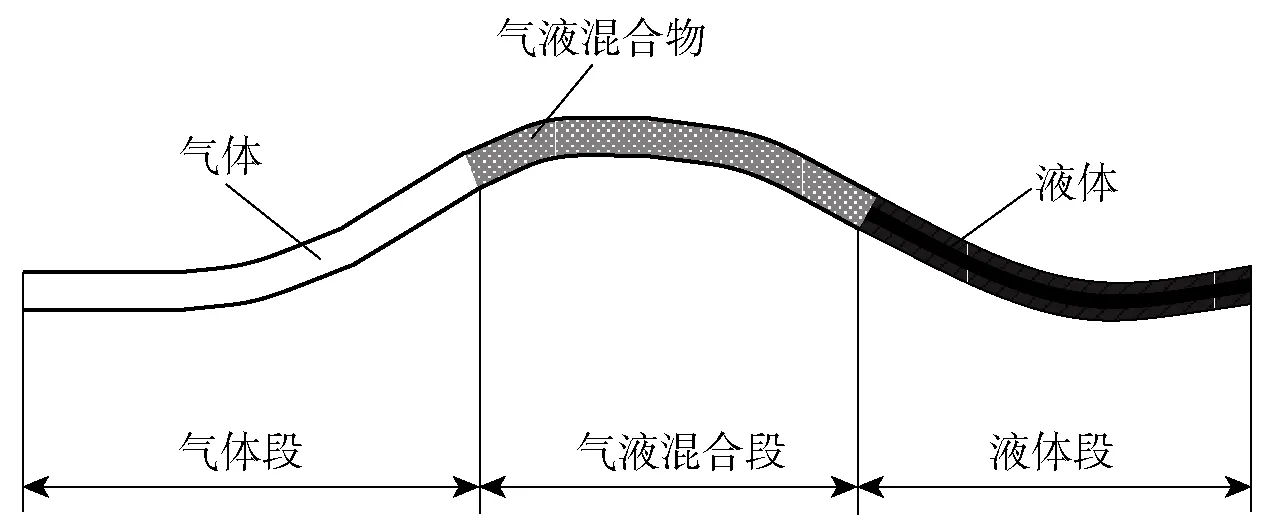
图1 充气排空过程某一时刻的水力状态

文献[15]对充气排液过程中管内持液率变化规律进行了研究，发现排空过程中气液混合段主要是以分层流和段塞流的形式存在，而且分层流存在的时间极短。根据Kelvin-Helmholtz的界面不稳定性准则，当气液间相对速度达到一定值时，界面的稳定性被破坏，分层流开始向段塞流转变。段塞流的压隆一般由两部分组成，一部分是流动阻力产生的摩擦压降，另一部分是由于气体压力变化产生的加速压降。Cazarez-Candia等[16]认为，尽管在段塞单元内部存在局部的速度变化，加速和减速对压降的作用可以抵消，对于整个段塞单元来讲总的压降变化为0 MPa.因此，在段塞单元内部不考虑加速压降。

1.1 流型转变过程

从分层流向段塞流的转变可用Kelvin-Helmholtz的界面波不稳定性理论来描述，当吸引力大于表面张力和重力的作用时，就会引起界面的不稳定，破坏分层流结构[17]。作用在波上的重力为

(hg-h′g)(ρl-ρg)g，

(1)

式中：hg、h′g为相临时刻气体高度；ρg和ρl分别为气体和液体密度；g为重力加速度；下标g和l分别代表气相和液相。

假设存在静止的波，吸引力将会导致波的增涨：

(2)

式中：p、p′为界面处相临时刻的压力；u′r和ur为相临时刻气相和液相在界面处的相对速度，由连续性关系，有

(3)

界面波增涨的条件是吸引力大于重力，使得分层流变得不稳定。将(1)式～(3)式合并，得到不稳定性的判据：

(4)

式中：

(5)

(6)

式中：Ag、A′g为相临时刻气液占有管路的截面积；θ为气液界面与管线轴向的夹角。

对于小的有限波，将(6)式围绕 展开泰勒级数，得

(7)

式中：

(8)

SI为相界面的湿周。

当管中液层高度较低时，有Ag=A′g、c2=1；管中液层较高时，有A′g→0、c2=0. 若满足这些条件，则有

(9)

式中：d为管路内径。

(9)式代入(7)式得到具有坡状液层的分层流向段塞流转变条件：

(10)

且

ur=ug-ul，

(11)

式中：ug和ul分别为气相和液相在界面的局部速度。

排空开始时，液相速度较快，气体流速较慢，气液两相的分层流状态比较稳定，但随着气体占有管线空间的变大和坡状液层的产生，使得气体的局部速度变大。当满足(11)式时，生成界面波，分层流开始向段塞流转变。

气液的局部流速可由(12)式和(13)式求出：

(12)

(13)

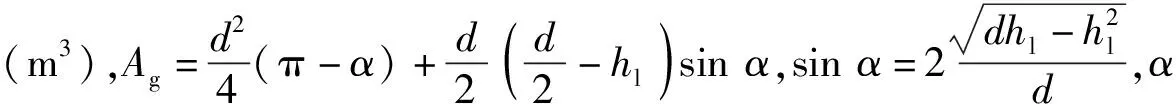
由于段塞流结构比较稳定，可以在很大的气液速度比范围内存在，因此段塞流是气液两相流中一种相对稳定的流型。另外，由于重力的作用，在气顶液前进的过程中会出现液体回流，也为段塞流的形成提供了条件。

1.2 段塞流阻力计算

在气液两相段塞流压降计算模型中，将整个段塞流分割成若干个段塞单元，每个段塞单元由液相段塞区(A-B段)和液层与气泡区(B-C段)组成部分，如图2所示。

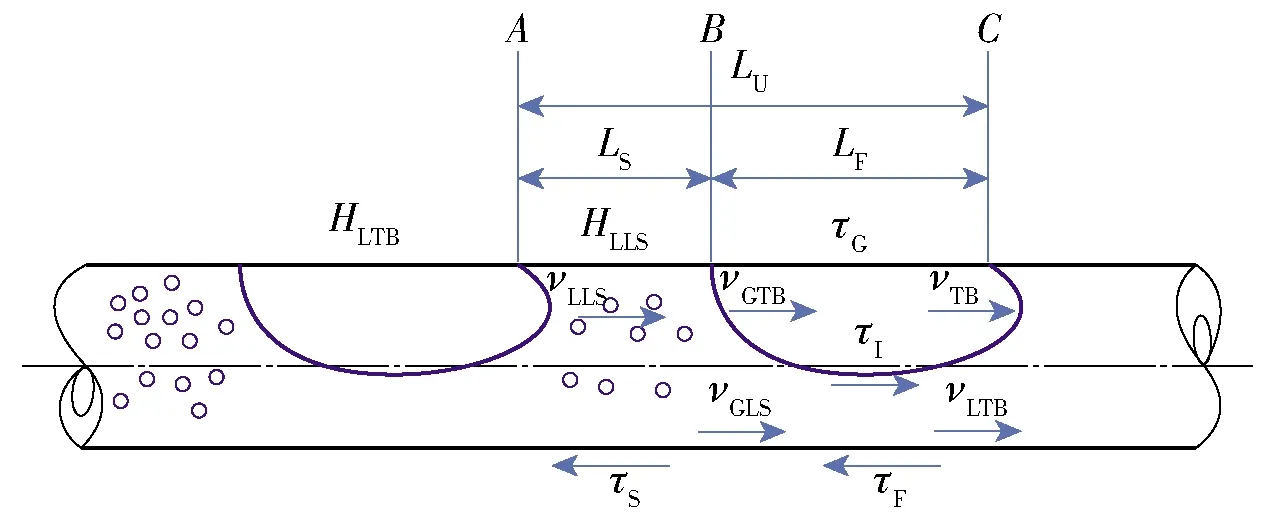
图2 充气排液时管内的段塞流模型

图2中：LS、LF、LU分别为液塞区、液层与气泡区和整个段塞单元的长度，且LS+LF=LU；HLLS、HLTB分别为液塞区和液层与气泡区的持液率；νLTB、νGTB分别为液层和气泡的当地速度；νTB为段塞单元的运动速度；vSL分别为气泡的绝对速度，uB为气泡的漂移速度，有vTB=vSL-uB；νLLS、νGLS分别为段塞内液相和气相的当地速度；τS、τF、τG、τI分别是液塞与壁面，液层与壁面，气泡与壁面以及气液两相界面间的剪切应力。

分别计算液塞区和气泡与液层区的流动阻力。液塞区的阻力可表示为

(14)

式中：Ss为液塞区的湿周，Ss=πd. 液层区的持液率相对较小，但排空过程中其长度可达液相段塞区的数倍，其压降对段塞单元影响很大。这一区域的阻力可表示为

(15)

式中：Sf为液层区的湿周。由于考虑了坡状液层的影响，将(15)式中的Sf写成hF的函数：

(16)

式中：hF是液层区内液层平均高度，一般取hF=0.6d[18].

LS可采用文献[18]提出的关联式进行计算：

ln(LS)=-26.8+28.5[ln(d)+3.67]0.1.

(17)

液塞内液体表观速度和液层区气泡速度之间的关系可表示为

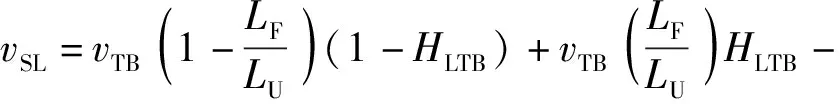
(vTB-vLLS).

(18)

目前多数学者认为段塞内的气泡存在漂移，即当管内形成段塞流时，由于段塞内的气泡与流动方向作反方向的漂移，因此管内气液混合段的运动速度并不等于液体段的速度，而是液体流速与气泡运动速度的差值。Benjamin利用伯努利定理对气泡表面进行分析，得到水平管长气泡漂移速度的计算式[19]：

(19)

回流到液层区的液体量与被液塞覆盖的量是相同的，可以表示为

(vTB-vLLS)(1-HGLS)=(vTB-vLTB)HLTB，

(20)

式中：HGLS为液塞区的气相持液率，在液塞区认为液相是连续的，也就是不考虑小气泡的存在，则HGLS=0；HLTB为液层区的持液率，可根据管路截面的几何关系[20]进行计算：

(21)

液层区速度和厚度的关系可以用Brotz提出的公式[21]来表示：

(22)

另外，对于一个段塞单元有

(23)

通过(4)式、(5)式和(8)式，即可求得LF.

τS、τF的计算方法分别为

(24)

(25)

式中：fS为液塞段的摩擦系数，fF为液层段的摩擦系数，两摩擦系数可由伯拉休斯关系式[9]确定：

(26)

(27)

C为流态系数，层流时C=16、n=1，紊流时C=0.046、n=0.2[22]，dF是液层区水力直径，dF=4AF/SF，μl为液体的动力黏度；ρS为液塞区的平均密度；ρF为液层区相对密度。

整个段塞流区域的压降可表示为

ΔPM=NΔPU，

(28)

式中：N为段塞数量；ΔPU=ΔPS+ΔPF.

1.3 液体段阻力计算

液体段摩擦阻力的计算可采用列宾宗公式：

(29)

式中：fM为液体段摩擦阻力系数，采用Fang修正过的关系式[23]进行计算：

(30)

Re为雷诺数，Re=uLdρl/μl；ll为液体段长度，可表示为

ll=l-lM-lg，

(31)

l为管路总长，lg为气体段的长度，lM为气液混合段长度，与液塞数量的关系为

lM=NlU.

(32)

为确定管流的阻力，必须确定液体段的长度，而确定液体段的长度必须要先确定气体段长度和气体段长度lg和气液混合段长度lM.

1.4 气体段长度计算

根据动量定理，得

(33)

式中：A为管路截面积(m2)；t为排空进行时间(s)。

由于气体段紧邻气液混合段，在段塞的尾部存在相当长的极薄液层[24]，混合段和纯气体段没有分明的界线，因此，将管内持液率小于0.1的部分作为纯气体段。根据前期的研究，对持液率小于0.1的时刻，排空压力、流量进行多元回归分析，得到气体段长度和终端液体流量随时间变化的关系[25]：

lg=-335.19+2.67t0.95+340.8qg+689.57pg，

(34)

ql=(0.54+0.004 1t-2×10-5t2+4.9×10-8t3)A/t，

(35)

式中：pg为入口空气压力(MPa)。

以气体流量7 m3/min、排气压力0.5 MPa为例，气体段长段和液体段长度随时间变化的曲线如图3所示，气液界面位置随时间变化的曲线如图4所示。

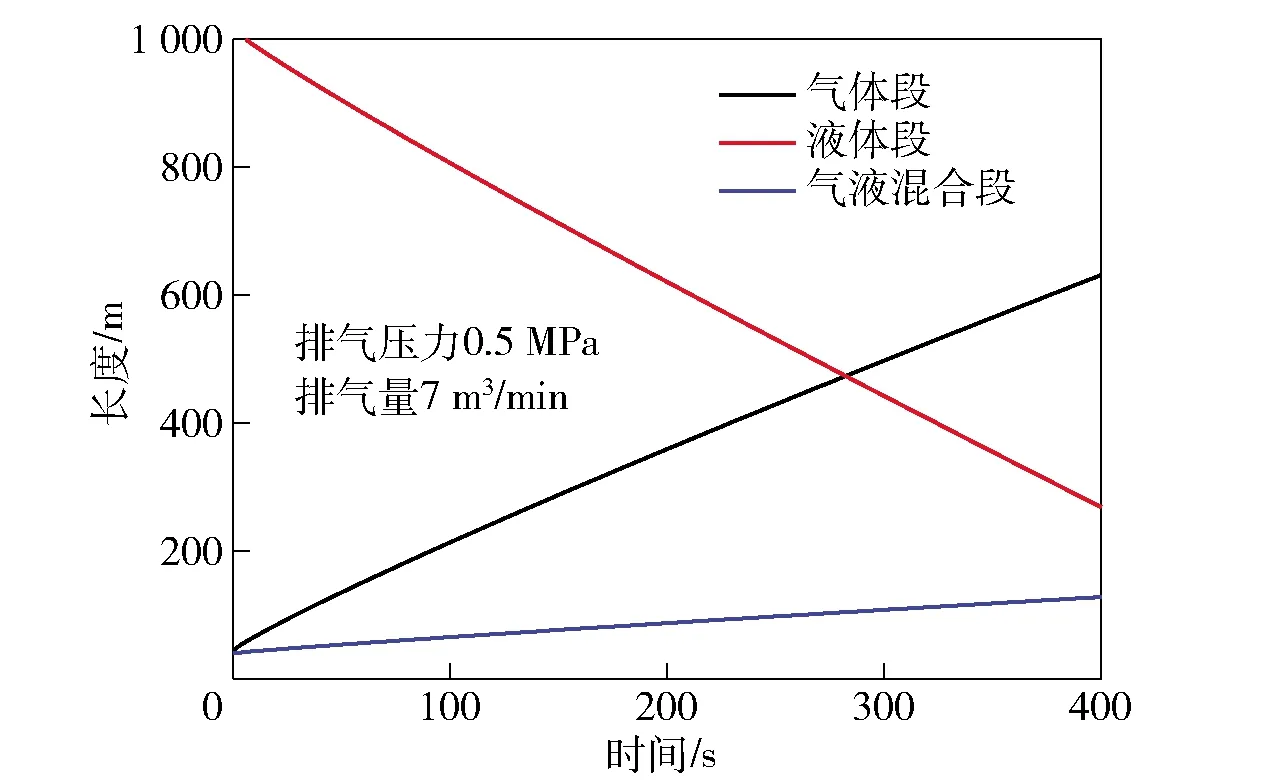
图3 气体段、液体段和气液混合段长度随时间变化

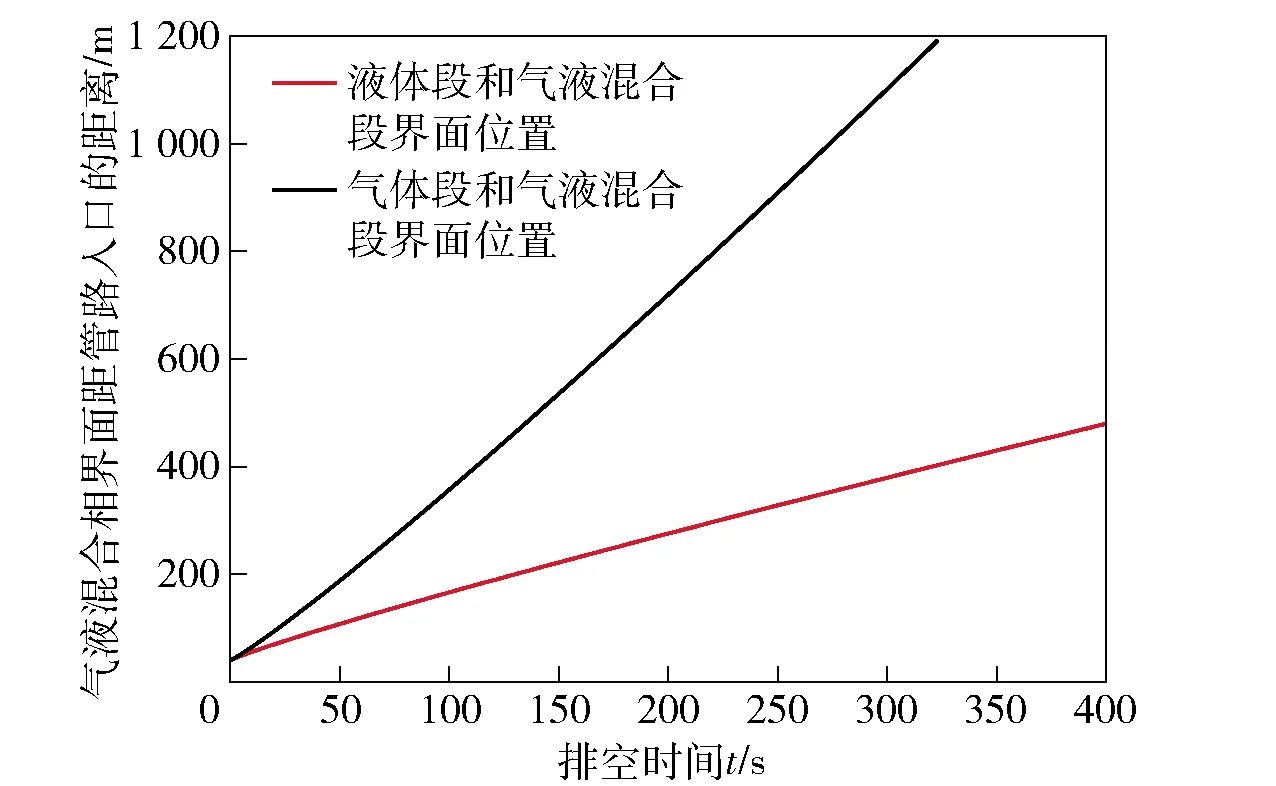
图4 气液界面位置随时间变化

终端液体流量随时间变化情况如图5所示。

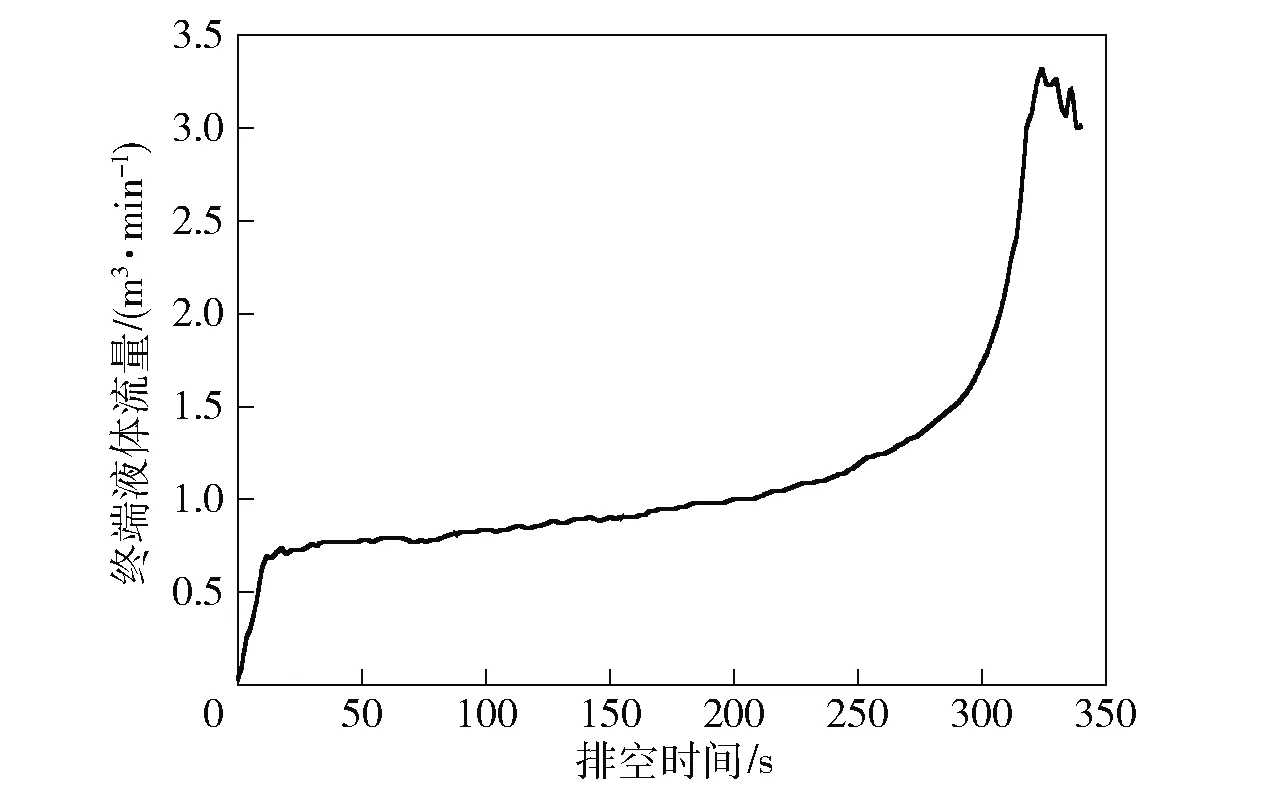
图5 终端液体流量变化

1.5 段塞单元周期的计算

根据何利民等[26]的研究，通过非线性回归和显著性检验，发现对液塞频率影响最大的因素是液相折算速度，其次是液塞速度和流体特性系数，气相折算速度影响最小,在总结Gregory&Scott关系式和Silva关系式的基础上，对段塞频率与气相、液相折算速度的关系进行了拟合分析[27]，得出

(36)

由此可得液塞出现的周期为

T=fst.

(37)

2 模型验证

2.1 实验系统

管路越长，阻力作用越明显，为保证实验验证的有效性，采用在室外搭设长距离管路的方法进行验证。铺设1 014 m的钢质管线(每根管子长6 m)，其中阻力测试段长度为1 098 m，管路水平直线铺设。为了保证流动阻力不受管壁光滑度的影响，使用的是绝对粗糙度ε=0.015 mm的钢管。管路沿线等距布置6个压力变送器，可根据需要随时调整管路长度，压力变送器型号为麦克传感器股份有限公司产MPM480型，量程范围为-0.1～2.5 MPa，固有频率为1 kHz，精度等级0.5%，稳定性和复现性好，采用引压接头将其安装在管线上，并配有密封胶圈。管路首末端分别布置气体流量计和液体流量计。气体流量计选用北京凯安达仪器仪表有限公司生产的KDBT-100型涡轮流量计，流量计的量程范围为20～400 m3/h，综合精度等级为1%，公称压力1.6 MPa；液体流量计选用合肥精大仪表股份有限公司生产的AVX-100-DDL-123型智能涡街流量计，计量范围0～270 m3/h，公称压力4 MPa，流量计均采用法兰夹装连接。管路进口设置空压机为管路充气，空压机为螺杆式空压机，最大排气压力和排气量分别为0.7 MPa和10 m3/min.管路出口设有储液罐，用于盛装管内排出的油品，经泵送入管线后重复使用。压力和流量信号的采集使用的是Visual Basic软件开发的数据采集系统，信道数量为16，采集频率为1 000 Hz.测量仪器的不确定度分析如表1所示，实验流程如图6所示。

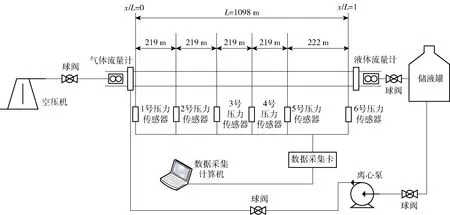
图6 实验流程图

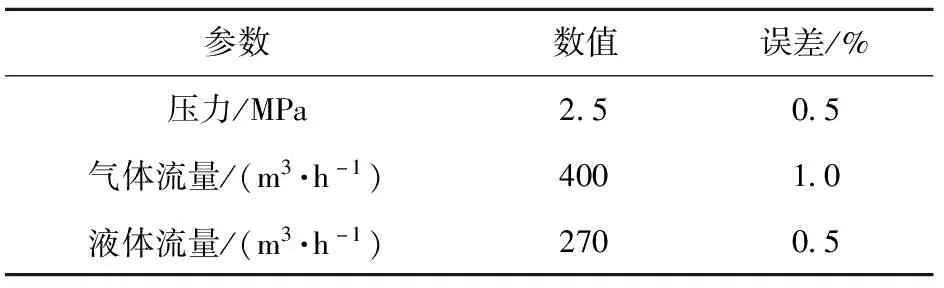
表1 实验测量不确定度分析

实验之前，将管路两端的阀门关闭，开始时，先打开空压机和其出口的阀门，当空压机压力稳定在0.5 MPa左右，同时打开管路入口和末端阀门开始排液，排液时间从开阀瞬间开始计算。实验参数如表2所示。

表2 实验参数

2.2 实验结果分析

实验测得的管路摩擦阻力pf=p1-p6，重复上述实验多次，取其中两次结果，分别如图7和图8所示。

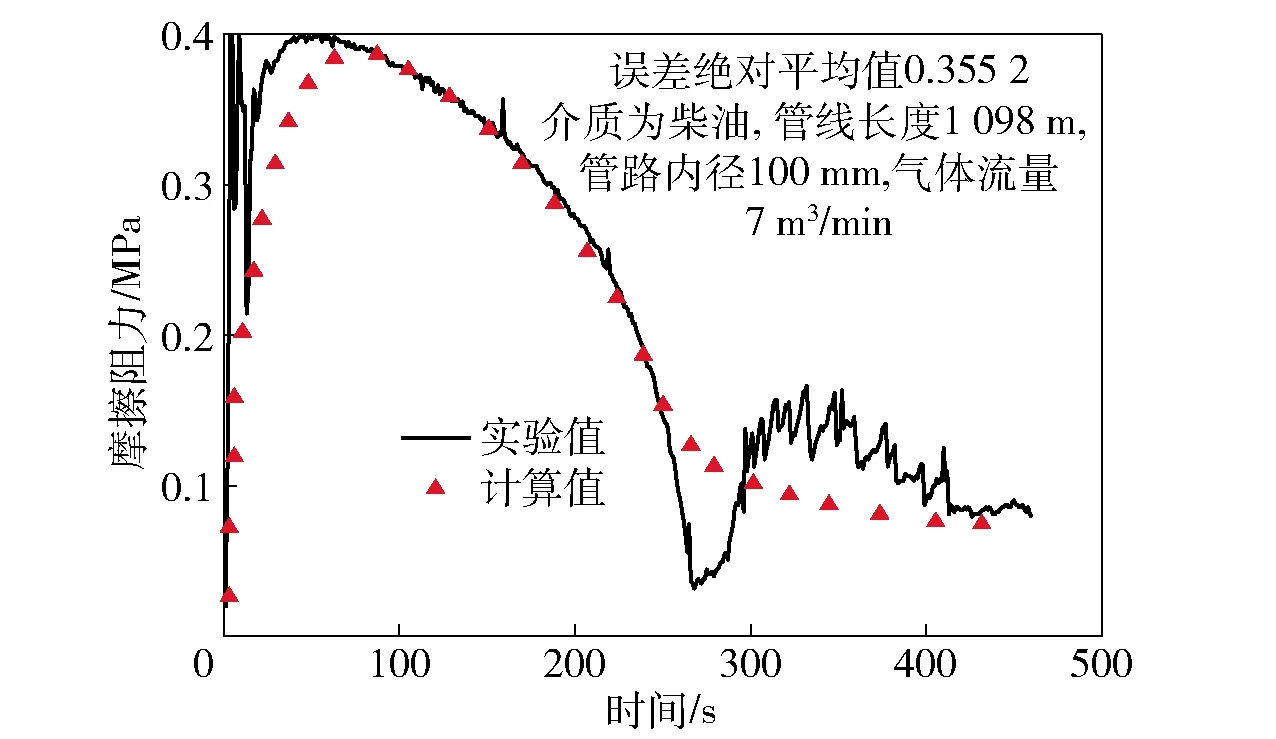
图7 第1次实验验证

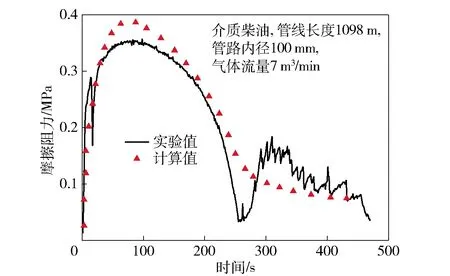
图8 第2次实验验证

从实验数据和关联式的计算结果对比情况看，在排液前期吻合程度较高，但在排液后期，计算值与实验值有一定的误差。在实验过程进行到280～300 s时，各次实验都出现了摩擦阻力下降再上升的现象，关系式在这一区域上的误差最大，这是由于管内的纯液体段被完全排出管路，摩擦阻力以气液混合段为主，这说明气液混合段的摩阻计算对模型整体的计算准确性产生了影响。另外，在段塞频率的计算上采用的是何利民等[26]给出的关系式，关系式具有一定的局限性。但总体上看，上述方法总体上能够反映排空过程管路摩擦阻力的变化趋势。

2.3 不同参数对模型准确性的影响

不同的参数可能对模型的准确性产生一定的影响，因此采用误差绝对值的平均值MR表征计算结果与实验之间误差，其定义为

(38)

式中：n是样本数量；yi,c为计算值，yi,e为期望值，i为样本序列。

通过不同工况下的实验对各参数的影响程度进行比较分析，工况参数如表3所示。不同工况对比如图9～图12所示。

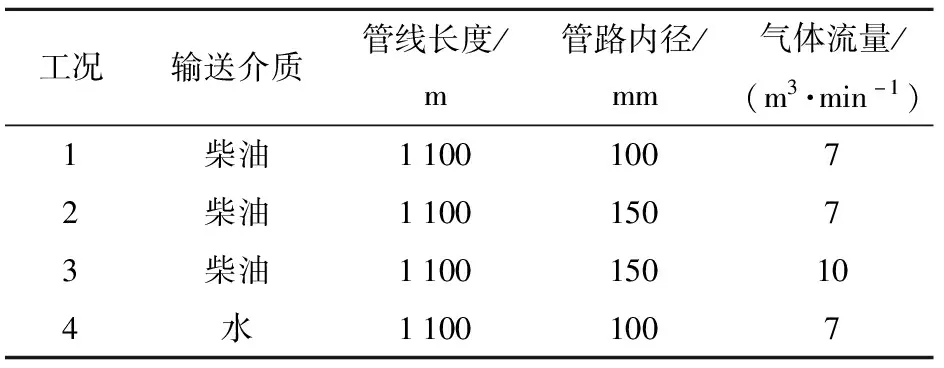
表3 不同工况参数

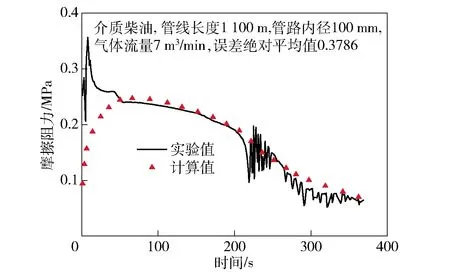
图9 工况1实验阻力随时间变化

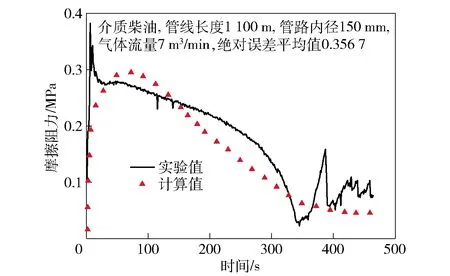
图10 工况2实验阻力随时间变化

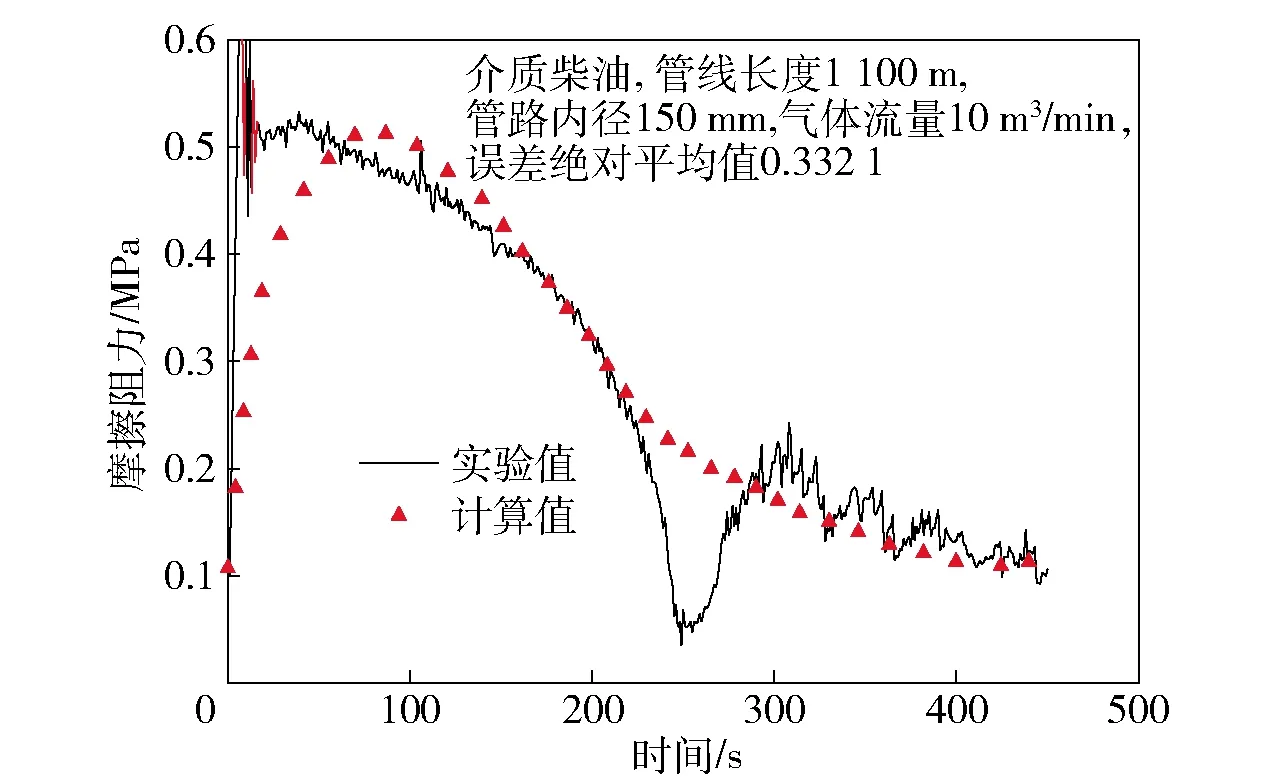
图11 工况3实验阻力随时间变化

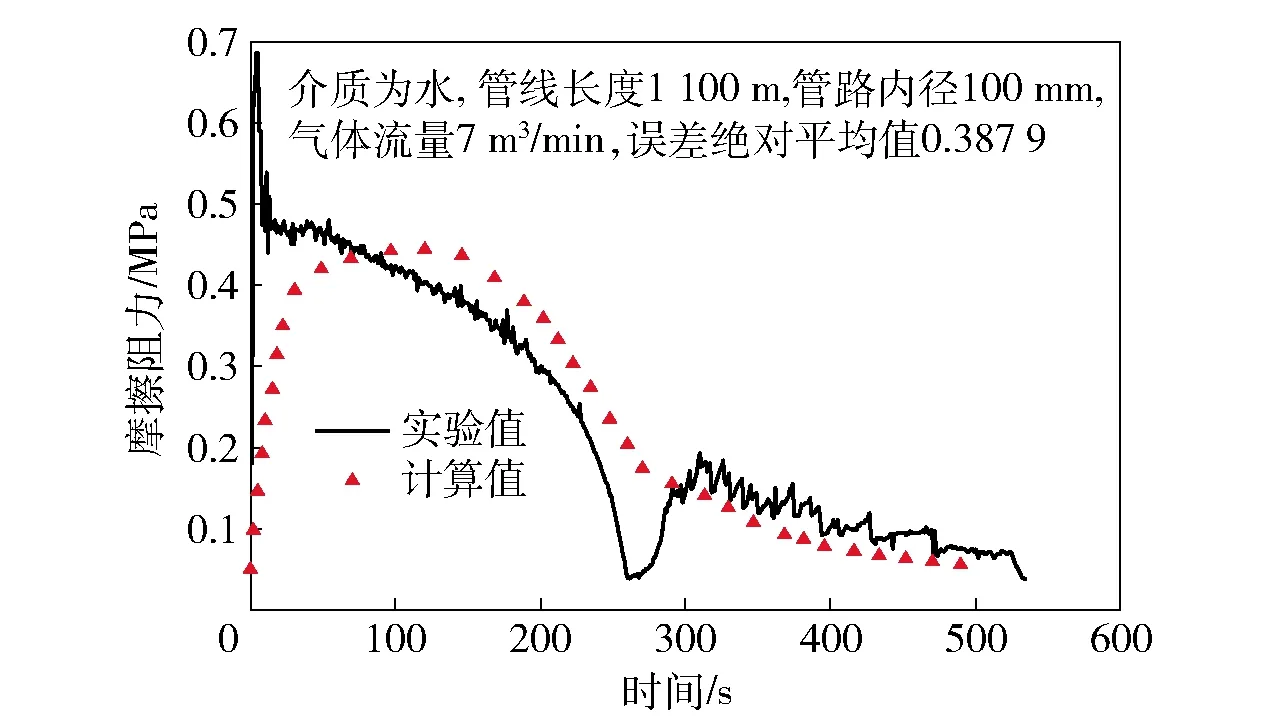
图12 工况4实验阻力随时间变化

将图7、图9、图10、图11、图12中的实验值和计算值进行计算，得到MR1=0.355 2，MR2=0.378 6，MR3=0.356 7，MR4=0.332 1，MR5=0.387 9. 对只改变一个参数的MR作差，即I=|MRi-MRj|，差值越大，说明该参数的变化对计算准确性的影响越大。管线长度影响的值为Il=|MR1-MR2|=0.023 4，管径的影响值为Id=|MR3-MR1|=0.008 7，气体流量的影响值为Igr=|MR4-MR1|=0.023 1，流体物性的影响值为If=|MR5-MR1|=0.032 7. 由此可见，输送液体的物性对本文计算方法准确性影响最大，而管路内径的影响最小。这是由于不同的流体，气液相间相互作用的强度不同，相间的相互作用也是影响系统阻力的一个因素。

3 结论

本文提出一种管道充气排空过程管路阻力的计算方法，将管路分为气体段、液体段和气液混合段，通过分别计算每一段的摩擦阻力而得到整个管路阻力特性：气液混合段的阻力计算是关键，以段塞单元的流动阻力为基础，通过理论分析和经验公式确定段塞流的长度和频率来计算气液混合段的阻力；由于液体段的长度不断变化，管内液体处于变加速直线运动状态，流动速度与进气流量和压力有关，通过实验数据拟合出液体段长度与时间、压力和流量的关系式，再利用列宾宗公式计算液体段的流动阻力。利用上述模型进行流动阻力计算，并与管线充气排液多种工况的实验数据对比，得到以下结论：

1)管路充气排液过程管内的流动阻力随时间呈非线性变化，在前2/3时间段内，管流的阻力主要来自于纯液体段，由于纯液体段长度的不断变化，管流阻力随时间变化曲线呈近似抛物线；在充液进行到2/3时，管流阻力骤降，这是管流阻力主导因素发生改变的一个拐点，此后，管流阻力又缓慢增加，系统阻力主要来自于气液混合段，并伴有较剧烈的压力波动。因此，管路充气排液过程的阻力变化可分为2个阶段，以气液混合段和纯液体段分别计算管流阻力也是合理的。

2)计算模型在排液过程的前2/3时间段内与实验数据吻合较好，但在后面1/3时间段内，计算值与实验值有一定的误差，误差主要来自气液混合段：一是对段塞流出现频率的估计采用的是何利民等[26]给出的经验关系式，但段塞频率具有一定的随机性，影响因素也很多，很难拟合出适用于多种条件下的关系式；二是气体跟随液体排出管路时会产生加速压降，模型没有考虑加速压降和段塞流压力波动对的阻力的影响。从总体表现看，该模型与实验数据的相关性较好，可以用于管道充气排液过程的阻力计算。

3)采用误差绝对平均值对影响模型准确性的参数进行了分析，影响最大的是油品物性，如黏度、密度、表面张力等，而管路内径、管线长、气体流量的影响较小。由此可见，不同的气液两相流系统特性差距很大，特别是伴有相间传质的成品油管道，对强挥发性液体的两相流管路还应进一步深入研究。