基于多物理场耦合的毛细水高度研究
邓改革, 何建国, 康宁波
(1.宁夏大学 土木与水利工程学院, 银川 750021; 2.中国矿业大学银川学院 信息工程学院, 银川 750021; 3.宁夏大学 农学院, 银川 750021)
毛细作用是指浸润液体在细管里升高和不浸润液体在细管里降低的现象,是液体的惯性力、黏性力、毛细力与重力等共同作用的结果[1]。土壤毛细水是靠毛细吸引力而保持于土壤毛细孔隙中的水。土壤毛细水上升高度对包括路基冻坏以及农田土壤次生盐渍化等在内的众多过程具有重要的影响,目前国内外学者在毛细水上升高度方面已经开展了大量的研究工作但尚不深入。
于丹等[2]进行了不同干密度重塑黄土的毛细上升速率和最大高度的研究,发现毛细最大上升高度与干密度之间非线性关系,而是呈现近似抛物线的函数关系。李先瑞等[3]针对改性黄土进行了垂直方向毛细水上升作用的研究,发现石灰能够有效降低土体内的含水率,且随着含量的增加,吸水作用越明显,而水泥对于土体内部结构的改性作用更大,提升土体强度和遇水稳定性,阻碍毛细水上升作用显著。肖红宇等[4]进行了基于黏性土分形特征的毛细水上升高度研究,推导出土体内毛细水上升高度预测公式,并将公式预测结果与实测结果进行了对比分析,发现误差在工程允许范围之内,具有一定的实际应用价值。落宇杰等[5]进行的压实黄土状粉土毛细特性试验发现,毛细水上升的速率随毛细上升高度的增加而逐渐衰减。袁玉卿等[6]通过室内试验研究了豫东黄泛区粉砂土毛细水上升规律及控制技术,研究发现随时间的延长毛细水上升高度逐渐稳定,毛细水上升速度与压实度呈反比,级配碎石、水泥稳定土、纤维水泥稳定土能有效阻隔毛细水上升。
胡明鉴等[1]进行了砂性土条件下,不同粒径及潜水矿化度组合的毛细水上升试验,研究了不同粒径及潜水矿化度下对毛细水上升高度及上升速度的规律。王聪[7]、栗现文[8]等通过观测毛细水上升速度和高度,研究不同浓度盐溶液和盐渍土对毛细水上升的影响,并对这些影响因素进行机理分析。
魏样[9]、童玲[10]等分别研究了石油及柴油污染对土壤毛细水上升特性的影响。章求才等[11]研究了温度和气压对某金属矿山尾矿坝中毛细水上升规律的影响,发现温度对毛细水上升的影响较气压大;在毛细水上升初期,温度、气压对毛细水上升规律的影响不大,但在上升后期其影响逐渐明显。
Masoodi等[12]采用达西定律模拟了液体向由纤维素和高吸水性纤维制成的纸状膨胀多孔介质中的芯吸现象。提出了新的毛细模型,将多孔介质中达西定律与质量守恒方程相结合,通过向质量守恒方程添加附加的汇或源项,以说明基质的膨胀和液体吸收。新模型预测芯吸速率较修正的沃什伯恩方程预测芯吸速率更好。
Aghajani等[13]提出了一种改善土壤中毛细水上升高度准确性的方法,该方法重新考虑了传统方法中被忽略的毛细区域中水分和吸力的变化,试验结果表明,改进的方法比以前的毛细管上升解决方案更加准确和通用。
Fili等[14]进行了采用多相格子玻尔兹曼方法(LBM)检验土壤持水曲线中毛细现象的研究。LBM模型首先针对基准问题进行验证,然后用于模拟静态粒子阵列,以此来研究初始流体密度分布对系统毛细管响应的影响。结果表明,湿润锋的统一性直接影响土壤骨架毛细响应峰值的大小。
Zhou等[15]研究了非饱和土的抗剪强度与毛管持水曲线的关系,提出了一种新的、考虑吸附水毛细凝结的非饱和土壤保水模型。模型中,将土壤的饱和度分为基于毛细管水的饱和度和基于吸附水的饱和度。通过对部分饱和的双圆柱系统的分析,提出了一种新的非饱和土抗剪强度准则。研究结果将大大改进对试验数据预测的准确性。
以上对毛细水高度的研究多侧重于室内土柱试验,研究内容多集中于不同土质结构、矿化水、污染物以及外界温度压力等方面,取得了一定的研究成果。而基于多物理场耦合的毛细水上升高度机理方面研究尚未见公开报道。本文使用多孔介质中多相流理论,通过多物理场耦合软件COMSOL Multiphysics建立模型,耦合多孔介质界面中达西定律和相输运,最后通过实验室土柱试验对模拟结果进行验证。研究结果将对弄清毛细水上升机理提供新的思路和方法。
1 研究方法
1.1 数值模拟研究
1.1.1 理论模型 在经典的多孔介质模型中,构成其基体的尺寸及其之间的孔隙在毛细吸水过程中保持恒定。目前计算毛细水上升高度的模型主要有两种,一种基于Lucas-Washburn方程,另一种基于达西定律[12]。这两种方法在计算毛细上升高度方面均存在缺陷,致使理论计算值与实际结果之间偏差较大。下面介绍多物理场耦合多孔介质中的多相流计算模型,该多物理场耦合了多孔介质界面中的达西定律和相输运。多孔介质界面中的相输运遵循润湿或非润湿流体体积分数的独立方程:
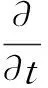
(1)
式中:εp为孔隙率;ρi为第i相的流体密度(kg/m3);∇为梯度算子;si为相的体积分数;κ为渗透率(m2);κri为相对渗透率(给定流体的饱和度的函数);μi为流体的动态黏度(Pa/s);pi为压力(Pa);∇pi为压力差(Pa);g为重力加速度(m/s2)。
由于两相的体积分数之和为1,因此可以从以下公式计算剩余的体积分数:
s1=1-s2
(2)
式中:s1为非润湿相体积分数;s2为润湿相体积分数。
毛管压力pc作为润湿相sw(模型中为s2)的饱和度和入口毛细管压力pec的函数进行计算。通过使用Brooks-Corey模型[16-18],毛管压力由下式得出:
(3)
式中:λp为孔隙分布指数;pec为入口毛细管压力。基于Brooks-Corey模型,湿相和非湿相的相对渗透率由下式给出:
(4)
(5)
式中:κrs为湿相相对渗透率;κrsn为非湿相相对渗透率。
通过达西定律接口将达西定律与连续性方程相结合:
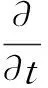
(6)
式中:ρ为流体密度;μ为流体动力黏度;κ为渗透率(m2)。
1.1.2 模拟参数确定 以1,2,3号管土柱为数值模拟的研究对象,建立模型水力边界条件:地下水位线在砂土柱的最底端并保持稳定,砂土柱顶端设置为自由边界[6]。由于竖管的对称结构,同时为了减小网格数量以提高计算效率,建立竖管的二维模型,所建立模型宽度为41 mm,高度为1 000 mm,并对所建立模型进行网格划分,建模相关参数见表1—2。计算时间为1 600 min,时间步长为5 min,通过COMSOL Multiphysics多物理场仿真软件,利用有限差分法对上述方程进行离散化求解。
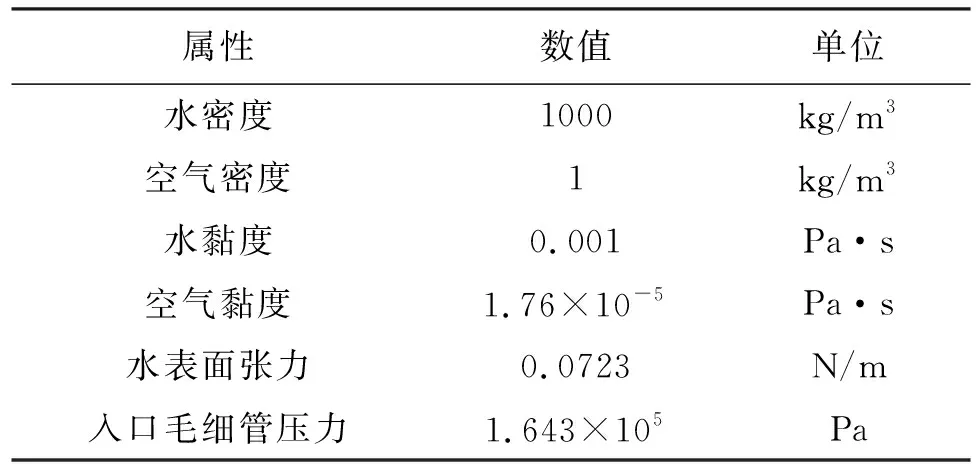
表1 水、空气和多孔材料的材料参数

表2 不同编号砂土多孔介质特性参数
1.2 土柱试验研究
本文采用竖管法研究毛细水上升高度。试验用砂土编号为#1,#2,#3,按照相关规范进行物理指标试验,测定相应参数,结果见表3。
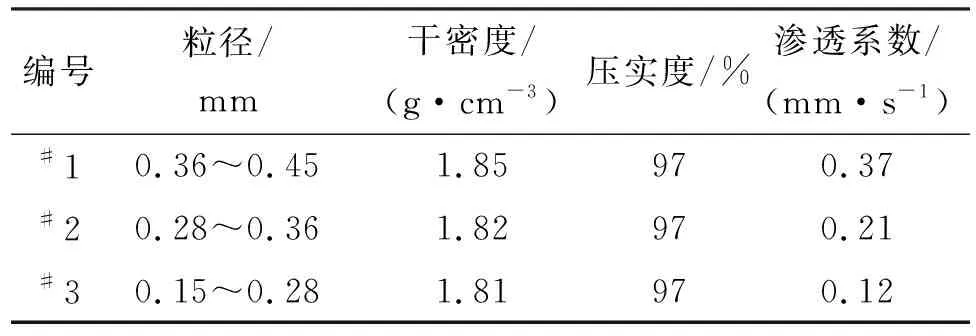
表3 试验用砂土物理参数
试验采用自制的毛细管水上升高度装置(图1)。装置由仪器支架、3支有机玻璃管、有机玻璃水箱、标尺、微型循环水泵及相连接的橡胶管组成。有机玻璃管长度为100 cm,内径41 mm,外径45 mm,顶端敞口可以与大气连通。将编号为#1,#2,#3的砂土分别装入编号为1,2,3的有机玻璃管中。三根有竖管放置在有机玻璃水箱托盘中,托盘高出水箱液面一定距离,通过微型循环水泵将水箱中水补充至托盘中,使托盘中液面保持恒定。

图1 毛细管水上升高度装置
毛细水上升高度主要试验步骤如下:将筛分配制好的一定质量的砂样,通过漏斗将土样装入有机玻璃管中,使其具有相同的压实度。打开微型循环水泵并开始计时,观测湿润锋的位置,记录毛细水上升高度与时间。前期毛细水上升较快,每隔10 min记录湿润锋所在位置,之后随着毛细水上升速度变慢,读数时间间隔相应加大。
1.3 现场试验研究
在实训基地内部选择合适的场地,在场地上方提前30 d布置遮挡物防止外界雨水渗入,然后开挖长宽高分别为1 m×1 m×0.8 m的土坑,通过水泵向坑底部供水,不断调整水泵的流量使水面保持恒定,通过钢卷尺读取土壤湿润锋位置的变化见图2。

图2 毛细水上升高度现场试验
2 结果与分析
2.1 数值模拟结果及分析
从图3可知在模拟1 600 min后1,2,3号管湿润锋位置高度分别为16.8,23.1,37.5 cm,该模拟结果与后面实验室室内土柱试验结果较为接近。由图4可知,在模拟初期毛细水高度随时间增加较快,在模拟后期毛细水高度增加缓慢并逐渐趋于稳定。在毛细水上升高度不高的情况下,由于基质吸力做功远大于水分重力势,所以毛细水上升速度较快;但随着高度的上升,重力势增加明显,基质吸力做的功相对减少,上升的速度就逐渐变慢[6]。
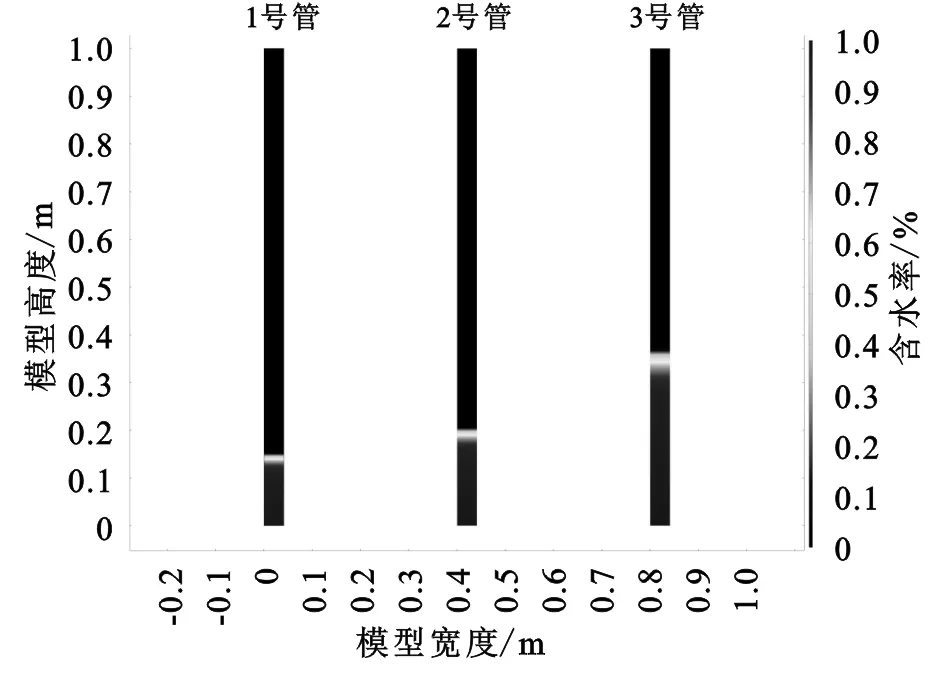
图3 不同编号毛细管1 600 min毛细水高度

图4 3号管7个不同时刻毛细水高度情况
2.2 土柱试验结果及分析
由图5可知,毛细水上升试验开始的前120 min毛细水上升速度较快。试验开始供水的第2小时,1,2,3号管毛细水分别上升至14.2,18,28 cm,这表明在相同压实度条件下不同粒径的土柱毛细水上升高度不同。3号管(粒径范围:0.15~0.28 mm)毛细水上升高度高于1号管(粒径范围:0.36~0.45 mm)及2号管(粒径范围:0.28~0.36 mm),说明砂土粒径越小毛细水上升的高度越大。随后毛细水高度继续增大,但是其上升速度逐渐减小。至510 min,1,2,3号管毛细水分别上升至14.6,19.6,34 cm。

图5 毛细水前510 min上升高度
由图6可知,在随后的试验时间内,试验土柱内毛细水高度持续增加,3号管毛细水高度最大,2号管次之,1号管最小。至1 600 min 1,2,3号管毛细水分别上升至15.6,22.0,37.5 cm。毛细高度随时间变化曲线斜率代表毛细水上升速度(图7),前120 min曲线斜率较大,表明毛细水上升速度较大,随后曲线斜率逐渐减小,毛细水上升速度也随之逐渐减小但并未停止,毛细水高度增加缓慢并逐渐趋于稳定。
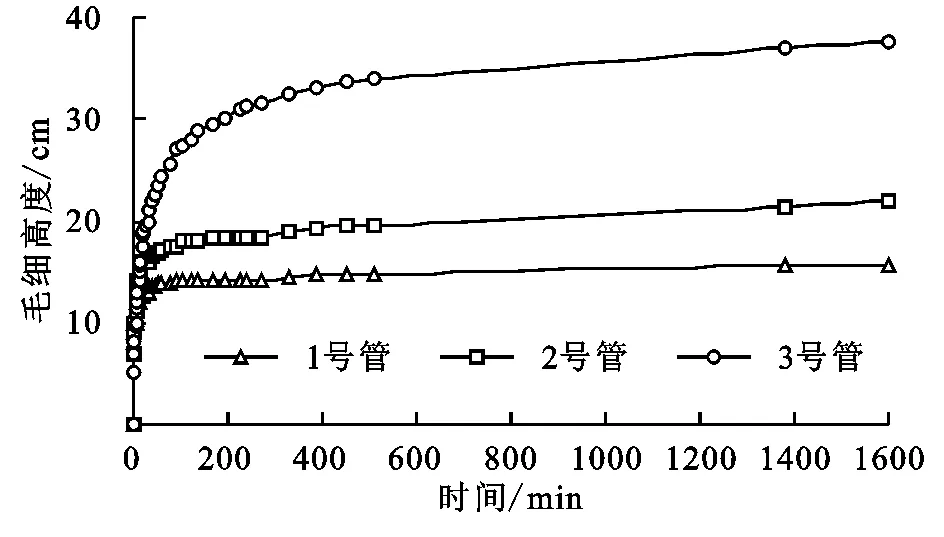
图6 毛细水1 600 min上升高度
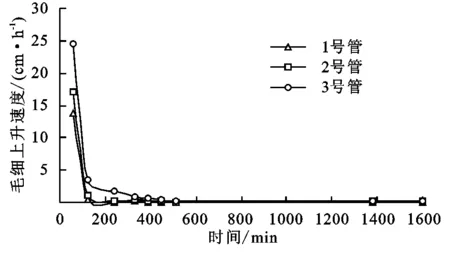
图7 毛细水上升速度随时间变化(0~1 600 min)
利用Origin软件,对图7数据的曲线进行函数拟合,所得关系式见表4。上升高度关系式两边对时间求导即可得毛细水上升速度表达式(表4)。

表4 毛细水上升高度拟合关系式
由表4可知,毛细水上升高度符合幂函数性质,为增函数,其变化特征是初期高度增加快,到一定程度后增加缓慢。而毛细水上升速度属于指数减函数,毛细水上升速度随时间减小。
将数值模拟结果与室内试验结果进行对比(表5),在误差范围内数值模拟与室内试验结果吻合较好。
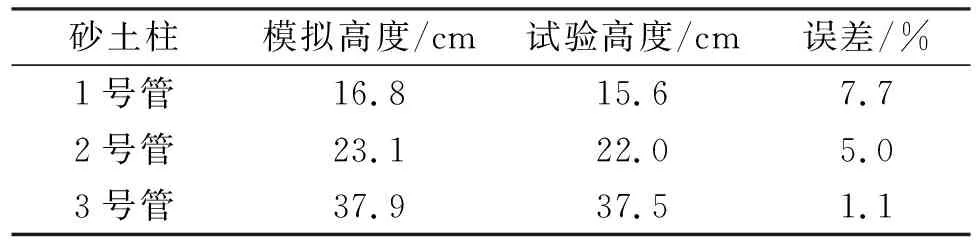
表5 模拟高度与试验高度对比
2.3 现场试验结果及分析
由于现场土坑中砂土参数与3号管中砂土参数较为接近,因此图8试验数据与3号管试验数据较为接近。通过分析数据可知毛细高度在30 cm以内,现场试验毛细高度小于实验室内土柱试验高度,其试验误差小于10%,当毛细高度超过30 cm后,试验误差逐渐增大至15%左右。现场观测发现,土坑中30 cm以上高度区域砂土粒径增大,且砂土中石块等杂物增多,对毛细水上升高度产生了影响。将试验误差考虑在内,可以认为现场毛细水上升规律与室内土柱试验以及多物理场仿真结果相吻合。

图8 毛细水1 600 min上升高度现场试验
3 讨论与结论
相同压实度不同粒径砂土柱内,毛细水上升高度与时长近似呈幂函数关系,为增函数,其变化特征是初期高度增加快,到一定程度后增加缓慢;毛细水上升速度与时长近似呈指数函数关系,为减函数,毛细水上升速度表现为初始阶段较大但随后迅速减小以致各组间差异不明显[8]。
在本试验中,相同压实度不同粒径砂土柱毛细水上升高度由大到小依次为:3号管(粒径范围0.36~0.45 mm),2号管(粒径范围0.28~0.36 mm),1号管(粒径范围0.15~0.28 mm),毛细水上升高度与砂土粒径呈负相关,总体表现为粒径越小,毛细水上升高度越大。在较小粒径条件下,黏性力的作用较强,在小粒径范围内起主要作用。相反,在大粒径范围下,重力作用表现更加明显,尤其是到毛细运移的后期,重力的影响增大,作用不可忽略[19]。砂柱粒径越小其内部毛细孔隙越小,毛细管力越大,毛细润湿峰上移迅速,同样时间间隔内,上升距离较高,且在试验结束时的高度也远远高于大粒径的高度[19]。这一结论和胡明鉴[1]、董斌[19]等的研究结论具有相同之处。
本文通过耦合多物理场多孔介质中达西定律和相输运,较好地模拟了毛细水上升高度,并且在试验误差范围内理论值与室内试验结果吻合较好,该研究方法在其他参考文献中尚未见公开报道。
压实度作为土柱试验的参数之一对毛细水高度具有一定的影响,本文仅研究了相同压实度条件下不同粒径的毛细水高度,而基于多物理场耦合条件下,不同压实度对毛细水高度的影响尚有待今后进一步研究。
试验用砂土作为一种多孔介质,其内部毛细流动现象是由惯性力、黏性力、毛细力与重力共同作用产生的,但在不同毛细高度各项作用力对毛细上升的贡献并不相同,这也是进一步理解毛细流动现象机理的关键所在[19]。
由于现场砂土粒径及土中杂物的影响使得现场试验与实验室试验及数值模拟结果存在一定的误差,但是将试验误差考虑在内,可以认为现场毛细水上升规律与室内土柱试验以及多物理场仿真结果相吻合。该结论应用于工程领域时,应该充分考虑现场因素对毛细水高度的影响,以现场试验作为补充,尽量减小试验误差。

