关于强-Drazin逆的Cline 公式

张维玺，郭世乐，陈焕艮

(1. 杭州师范大学理学院，浙江 杭州 311121； 2. 福建技术师范学院电子与信息工程学院，福建 福清 350300)

在本文中，所有环都是具有单位元的结合环.N(R)为环R中所有幂零元的集合.对于任意元素a∈R，记元素a的交换子为comm(a)={x∈R∶ax=xa}.元素a称为有Draizn逆aD，若

aaD=aDa,aD=aDaaD,a-a2aD∈N(R).

a∏表示1-aaD对于任意一个有Draizn 逆的元素a∈R.若ab具有Drazin逆，则ba也具有 Drazin逆，并且(ba)D=b((ab)D)2a，这个公式被称为Cline 公式.元素a∈R称为有强-Drazin逆，若存在元素x∈R满足

x2a=x,ax=xa,a-ax∈N(R).

这里x是唯一的，并称为元素a∈R的强-Drazin逆.文[1]研究了它的许多基本性质.正如我们所知，元素a∈R具有强-Drazin逆当且仅当a可表示为可交换的幂等元和幂零元的和[2].一个复数矩阵A具有强-Drazin逆当且仅当它有特征值0和1[1].

1 多项式条件

下文将在条件a(ba)2=abaca=acaba=(ac)2a下研究关于强-Drazin逆的Cline公式.

定理1设R为环，且a,b,c∈R满足a(ba)2=abaca=acaba=(ac)2a，则ac具有强-Drazin逆当且仅当ba具有强-Drazin逆.

证明假设ac具有强-Drazin逆，则存在正整数n使得(ac-(ac)2)n=0.以下证明ba-(ba)2是幂零元.

(ba-(ba)2)3=(ba-baba)(ba-baba)(ba-baba)=

bababa-3babababa+3bababababa-babababababa=

bacaca-3bacacaca+3bacacacaca-bacacacacaca=

b(acac-3acacac+3acacacac-acacacacac)a=

b(1-ac)(ac-(ac)2)2a.

假设(ba-(ba)2)n=b(1-ac)(ac-(ac)2)n-1a，可得

(ba-(ba)2)n+1=(ba-(ba)2)n(ba-baba)=

b(1-ac)(ac-(ac)2)n-1a(ba-baba)=

b(1-ac)(ac-(ac)2)n-1a(ca-caca)=

b(1-ac)(ac-(ac)2)n-1(aca-acaca)=

b(1-ac)(ac-(ac)2)n-1(ac-acac)a=

b(1-ac)(ac-(ac)2)na=0.

由归纳法，求得ba-(ba)2是幂零元，因此ba具有强-Drazin逆.

相反地，假设ba具有强-Drazin逆，那么存在正整数m使得(ba-(ba)2)m=0.同理可得

(ac-(ac)2)3=(ac-(ac)2)(ac-(ac)2)(ac-(ac)2)=

(ac)3-3(ac)4+3(ac)5-(ac)6=

a(ba)2c-3a(ba)3c+a(ba)4c-a(ba)5c=

a(1-ba)(ba-(ba)2)2c.

由归纳法，通过计算易得(ac-(ac)2)m+1=a(1-ba)(ba-(ba)2)mc=0，因此ac-(ac)2是幂零元，所以ac具有强-Drazin逆.

□

推论1设R为环，且a,b,c∈R，那么ab具有强-Drazin逆当且仅当ba具有强-Drazin逆.

证明令c=b，那么由定理1可得结论，证毕.

引理1设R为环，a∈R.那么a具有强-Drazin逆当且仅当1-a具有强-Drazin逆.

证明见[1，引理3.3].

推论2设R为环，且a,b,c∈R满足a(ba)2=abaca=acaba=(ac)2a，那么1-ac具有强-Drazin逆当且仅当1-ba具有强-Drazin逆.

证明假设1-ac具有强-Drazin逆，由引理1可得ac具有强-Drazin逆.继而由定理1可得，ba具有强-Drazin逆.再次由引理1可得，1-ba具有强-Drazin逆.

相反地，假设1-ba具有强-Drazin逆，同理可得，1-ac具有强-Drazin逆.

□

进一步，我们还有：

定理2设R为环，且a,b,c,d∈R满足acd=dbd,bdb=bac，如果ac具有强-Drazin逆，那么bd具有强-Drazin逆.

证明假设ac具有强-Drazin逆，则存在正整数m使得(ac-(ac)2)m=0.以下证明bd-(bd)2是幂零元.因为acd=dbd,dbd=bac，进而计算

(bd-(bd)2)2=bdbd(1-bd)2=bacd(1-bd)2=

bac(d-2dbd+dbdbd)=bac(d-2acd+acacd)=

bac(1-ac)2d=b(ac-(ac)2)(1-ac)d.

假设(bd-(bd)2)n=b(ac-(ac)2)n-1(1-ac)d，可得

(bd-(bd)2)n+1=(bd-(bd)2)n(bd-(bd)2)=

b(ac-(ac)2)n-1(1-ac)d(bd-bdbd)=

b(ac-(ac)2)n-1(1-ac)(acd-acacd)=

b(ac-(ac)2)n-1(1-ac)(ac-acac)d=

b(ac-(ac)2)n(1-ac)d.

由归纳法可得bd-(bd)2是幂零元，因此bd具有强-Drazin逆.

□

推论3设R为环，且a,b,c,d∈R满足acd=dbd,bdb=bac，如果1-ac具有强-Drazin逆，那么1-bd具有强-Drazin逆.

证明假设1-ac具有强-Drazin逆，则由引理1可得，ac具有强-Drazin逆.继而由定理2可得，bd具有强-Drazin逆.再次由引理1可得，1-bd具有强-Drazin逆.

□

推论4设R为环，且a,b,c,d∈R满足acd=dbd,bdb=bac，如果(ac)k具有强-Drazin逆，那么(bd)k具有强-Drazin逆对于任意的正整数k.

证明假设(ac)k具有强-Drazin逆.当k=1时，由定理2可得bd∈R具有强-Drazin逆.现在假设k≥2.通过计算易得(bd)k=b(ac)k-1d.因为db(ac)k-1=(ac)k具有强-Drazin逆，可知b(ac)k-1d具有强-Drazin逆.因此(bd)k具有强-Drazin逆，证毕.

2 矩阵形式

分块矩阵的Drazin逆在许多领域有广泛的应用，如奇异微分方程、马尔科夫链等.下文将研究强-Draizn逆的Cline公式的矩阵形式.

定理3设R为环，且A∈Mm×n(R),B,C∈Mn×m(R)满足A(BA)2=ABACA=ACABA=(AC)2A，则AC∈Mm(R)具有强-Drazin逆当且仅当BA∈Mn(R)具有强-Drazin逆.

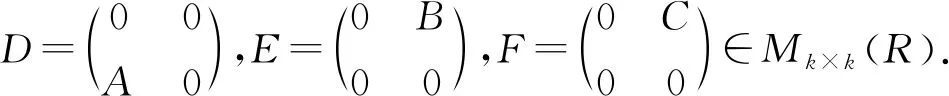
因为A(BA)2=ABACA=ACABA=(AC)2A,所以有

D(ED)2=DEDFD=DFDED=(DF)2D.

则由定理1可得，ED具有强-Drazin逆当且仅当DF具有强-Drazin逆.并且

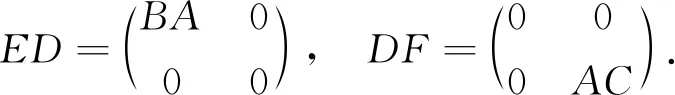
因此，AC∈Mm(R)具有强-Drazin逆当且仅当BA∈Mn(R)具有强-Drazin逆.证毕.

推论5设R为环，且A∈Mm×n(R),B,C∈Mn×m(R)满足A(BA)2=ABACA=ACABA=(AC)2A，那么Im-AC∈Mm(R)具有强-Drazin逆当且仅当In-BA∈Mn(R)具有强-Drazin 逆.

证明⟹.因为Im-AC∈Mm(R)具有强-Drazin逆，则由引理1可得AC∈Mm(R)具有强-Drazin逆.再根据定理3可得BA∈Mn(R)具有强-Drazin逆.再次由引理1可得，In-BA∈Mn(R)具有强-Drazin逆.

⟸.同理可证得.

□

定理4设R为环，且A,D∈Mm×n(R),B,C∈Mn×m(R)满足ACD=DBD,BDB=BAC，如果AC∈Mm(R)具有强-Drazin逆，则BD∈Mn(R)具有强-Drazin逆.

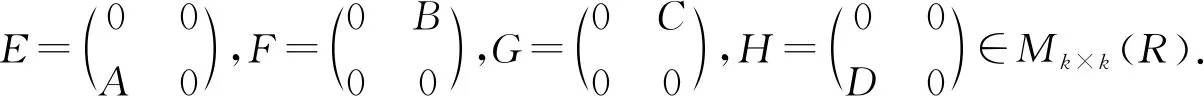
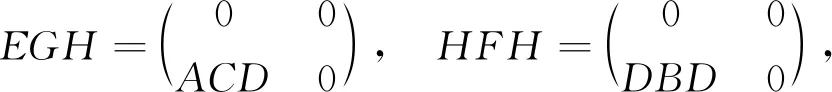
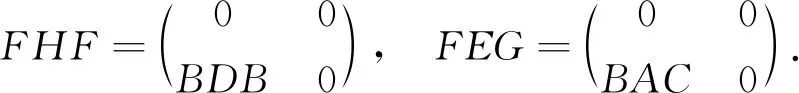
因为ACD=DBD,FHF=BAC,所以有

EGH=HFH,FHF=FEG.

□

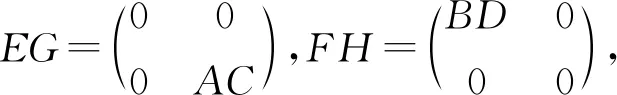
推论6设R为环，且A,D∈Mm×n(R),B,C∈Mn×m(R)满足ACD=DBD,BDB=BAC，如果Im-AC∈Mm(R)具有强-Drazin逆，那么In-BD∈Mn(R)具有强-Drazin逆.

证明⟹.因为Im-AC∈Mm(R)具有强-Drazin逆，则由引理1可得，AC∈Mm(R)具有强-Drazin逆.继而由定理4可得，BD∈Mn(R)具有强-Drazin逆.再次根据引理1可得，In-BD∈Mn(R)具有强-Drazin逆.

□

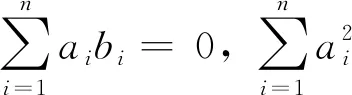
具有强-Drazin逆.

证明令A=P+Q，这里

□

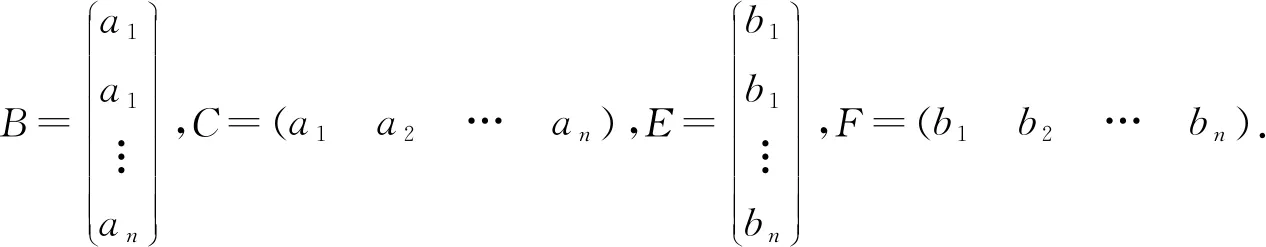
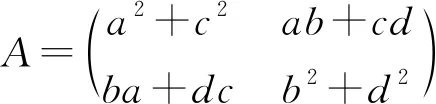
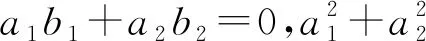
3 例子

最后，构造一些例子来说明所得的结论.

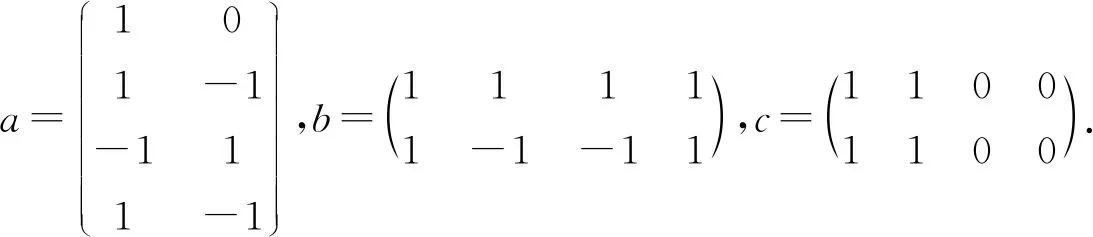
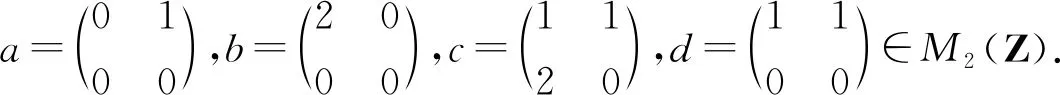
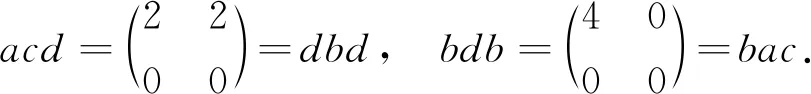
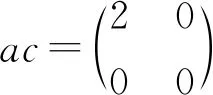
最后，说明推论7的条件“c+bd=0”是必要的.

例3令a=c=1，b=d=0∈Z.则有ac+bd≠0,a2+b2=1,c2+d2=1,令

容易验证A没有强-Drazin逆.