MARTINGALE REPRESENTATION AND LOGARITHMIC-SOBOLEV INEQUALITY FOR THE FRACTIONAL ORNSTEIN-UHLENBECK MEASURE∗

(孙晓霞)

School of Data Science and Artificial Intelligence,Dongbei University of Finance and Economics,Dalian 116025,China

E-mail:xiaoxiasun@dufe.edu.cn

Feng GUO(郭峰)

School of Mathematical Sciences,Dalian University of Technology,Dalian 116024,China

E-mail:fguo@dlut.edu.cn

Abstract In this paper,we consider the measure determined by a fractional Ornstein-Uhlenbeck process.For such a measure,we establish an explicit form of the martingale representation theorem and consequently obtain an explicit form of the Logarithmic-Sobolev inequality.To this end,we also present the integration by parts formula for such a measure,which is obtained via its pull back formula and the Bismut method.

Key words Fractional Ornstein-Uhlenbeck measure;integration by parts formula;martingale representation theorem;Logarithmic-Sobolev inequality

1 Introduction

A stochastic process(Xt)0≤t≤1is called a fractional Ornstein-Uhlenbeck process if it satisfies the stochastic differential equation

Quite a lot of interest has been paid to the study of the martingale representation and the Logarithmic-Sobolev inequalities for different measures.It is proved in[13]that Logarithmic-Sobolev inequality holds for the Wiener measure on the path space over a connected Lie group.For the Wiener measure on the path space over a Riemannian manifold,[17]gives the Logarithmic-Sobolev inequality with a bounding constant which can be estimated in terms of the Ricci curvature.Moreover,for such a measure,the Logarithmic-Sobolev inequality can also be obtained by embedding the manifold into a Euclidean space[3]and the martingale representation[5].For the Brownian bridge measure on loop space,the martingale representation and the Logarithmic-Sobolev inequality are investigated in[2,12,14].

The Logarithmic-Sobolev inequalities for measures can be obtained via their martingale representations,which in turn can be established by their integration by parts formulas.The integration by parts formulas for different measures are important in infinite dimensional analysis,and have been well studied.For instance,the integration by parts formula is investigated for the Wiener measure on the path space in[7,11,15],for the Brownian bridge measure on the loop space in[1,8,10,16],for the fractional Wiener measure under different integrals in[6,9],and for the fractional Ornstein-Uhlenbeck measure in[21].

ContributionsWe establish the pull back formula(Proposition 3.1)and an integration by parts formula for the fractional Ornstein-Uhlenbeck measure(Theorem 3.2).We give an explicit form of martingale representation theorem(Theorem 4.1)by the corresponding integration by parts formula.Consequently,we derive an explicit form of the Logarithmic-Sobolev inequality(Theorem 4.2)by the martingale representation theorem.

The paper is organized as follows:in Section 2,we give some preliminaries about fractional Brownian motions.We present in Section 3 the pull back formula and the integration by parts formula.In Section 4,we obtain the martingale representation theorem and the Logarithmic-Sobolev inequality for the fractional Ornstein-Uhlenbeck measure.

2 Preliminaries

Let(Ω,F,Ft,ν)be a filtered probability space,where Ω is the space of Rn-valued continuous functions on[0,1]with the initial value zero,ν is the fractional Ornstein-Uhlenbeck measure such that coordinate process(Xt(ω))0≤t≤1=(ωt)0≤t≤1satisfies(1.1),F is the ν-completion of the Borel σ-algebra of Ω,and Ftis the ν-completed natural filtration of ω.The space Ω is a metric space with the uniform metric

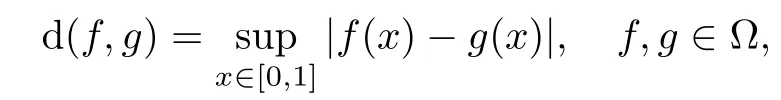
and the topology of uniform convergence is derived from this metric.

In what follows we consider fractional integral with H>1/2.Let

where h∈H and

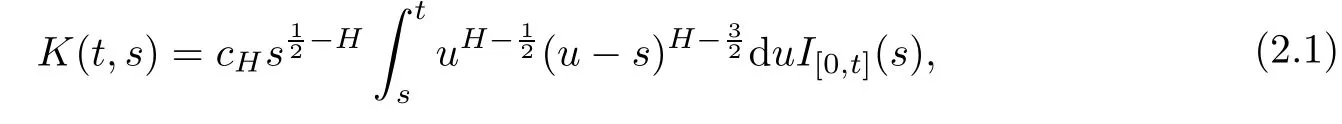
in which,for beta function B(·,·),

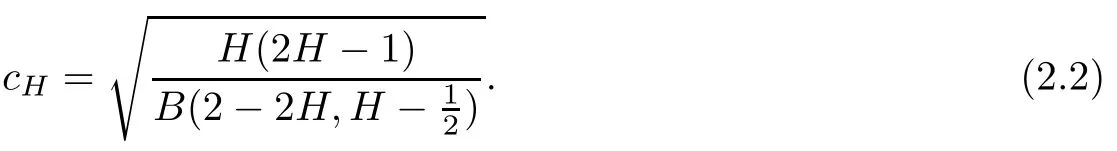
By the definition of Kh,for H>1/2,we have

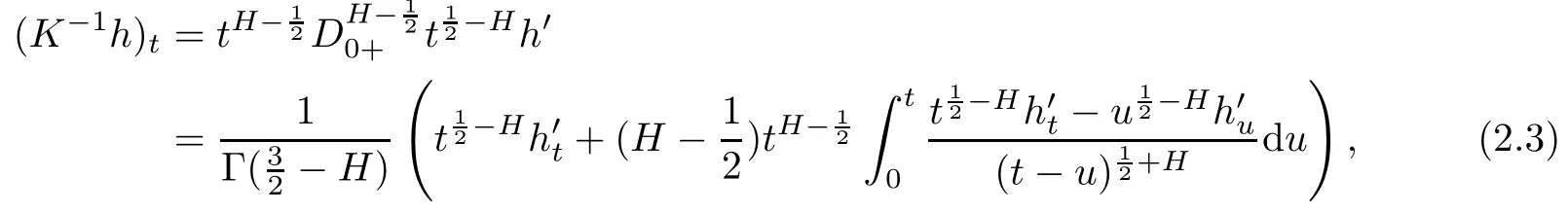
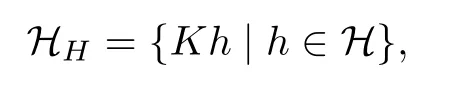
with scalar product

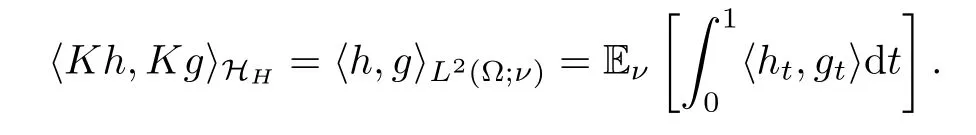
In fact,it is easy to check that HHis a Hilbert space.For Kh∈HH,the directional derivative of F along Kh is

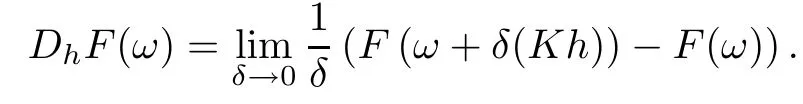
We denote all the smooth cylindrical functions on Ω by

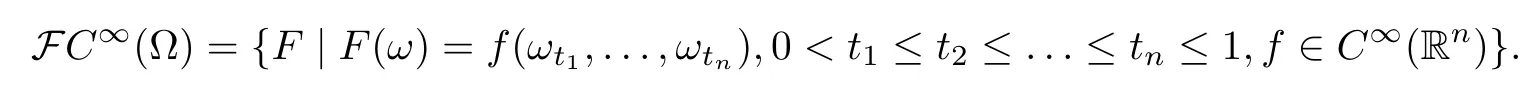
For F∈FC∞(Ω),the directional derivative of F along Kh is

where

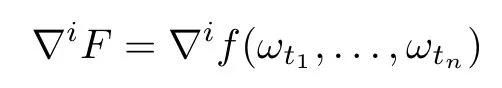
is the gradient with respect to the i variable of f.For F∈FC∞(Ω),the gradient DF:Ω→HHis determined by

Then,through the integration by parts formula(3.4),we can show that the gradient operator D is closable in Lp(ν)for all p and that FC∞(Ω)is a core.We denote again its smallest closure by D.Furthermore,Dom(D)denotes the domain of the smallest closure of D.

3 Integration by Parts Formula for Fractional Ornstein-Uhlenbeck Measure

To obtain the integration by parts formula for the fractional Ornstein-Uhlenbeck measure,inspired by the idea in[4],for any H∈H,we first construct an Rn-valued function(βt)0≤t≤1such that for any r∈(−∊,∊),the stochastic differential equation

has a solution(Xt(r))0≤t≤1satisfying

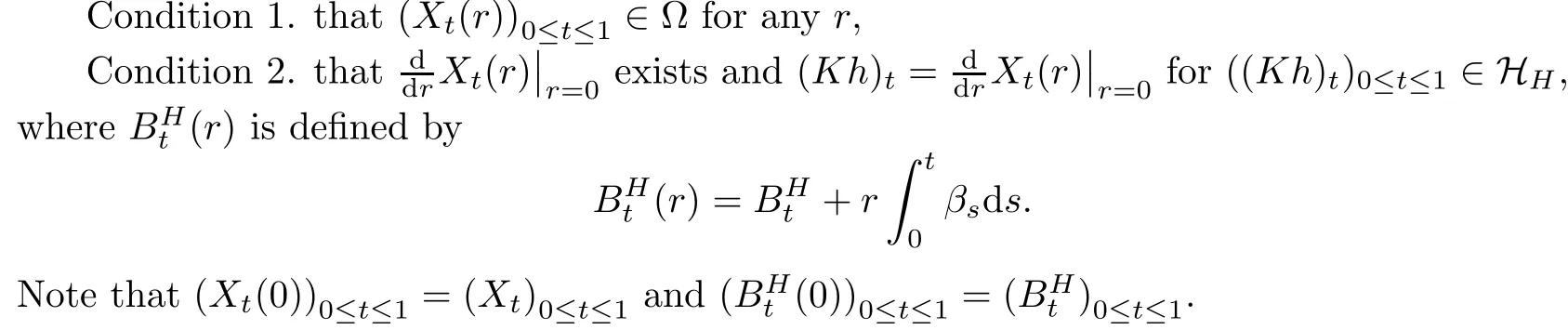
Proposition 3.1Suppose that h∈H.If(βt)0≤t≤1satisfies Condition 3 and Condition 3,then we have

ProofDifferentiating(3.1)with respect to r at r=0,we get

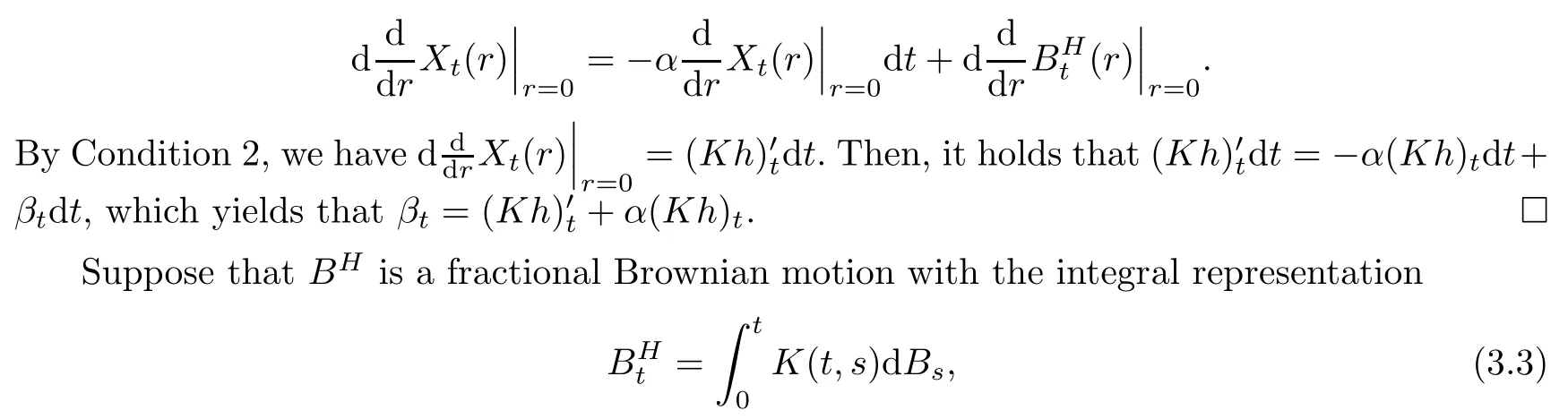
where(Bt)0≤t≤1is an n-dimensional Brownian motion under ν(see[6]).In the following we establish the integration by parts formula for the fractional Ornstein-Uhlenbeck measure ν via the pull back formula given in Proposition 3.1:

Theorem 3.2For F∈Dom(D)and Kh∈HH,the integration by parts formula for the fractional Ornstein-Uhlenbeck measure ν is

By Hölder inequality,

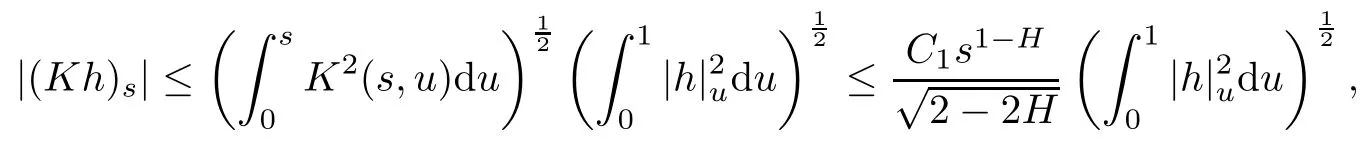
where C1satisfies

which is due to Theorem 3.2 in[6].Hence,for s∈[0,1],we have

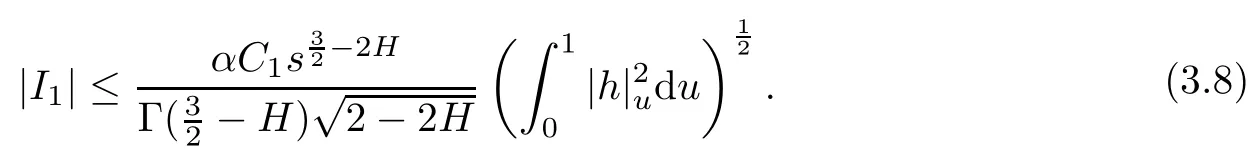
By[19,Theorem 3],there is a constant C2such that

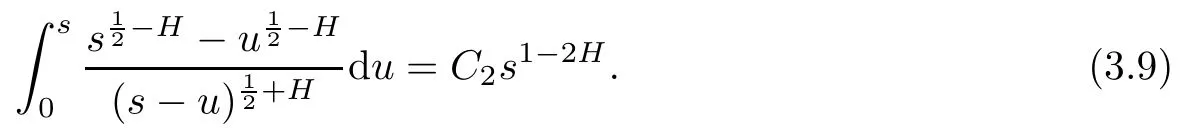
In fact,by replacing u with sv,we get

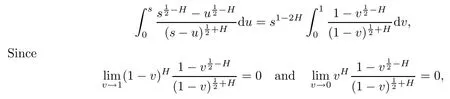
by the comparison test for improper integrals,(3.9)holds.Therefore,

Suppose that h is bounded adapted process,then,by(3.12),Eν[ρ1(r)]=1.It is easy to see that Z

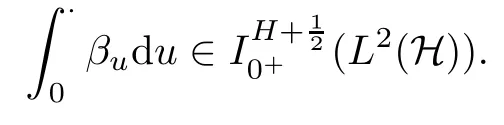
Therefore,by[19,Theorem 2],

Differentiating the above equation with respect to r,we obtain

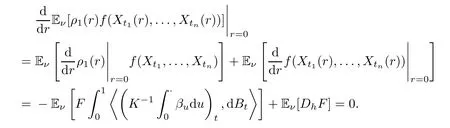
Hence,for the bounded adapted process h,we have the following integration by parts formula:

holds for bounded processes hn,then by(3.15)and(3.16),the integration by parts formula(3.13)holds for any adapted process h∈H.Moreover,since D is a closable operator,the integration by parts formula(3.13)holds for any F∈Dom(D). □

Now we have established the integration by parts formula for the fractional Ornstein-Uhlenbeck measure ν.In the next section we will study the martingale representation and the Logarithmic-Sobolev inequality for ν via the integration by parts formula using an idea similar to that employed in[12,18].

4 Martingale Representation Theorem and Logarithmic-Sobolev Inequality

To prove the Logarithmic-Sobolev inequality,we generalize the classical Clark-Ocone martingale representation theorem for Wiener measure to the fractional Ornstein-Uhlenbeck measure ν.The classical Clark-Ocone martingale representation theorem states that every martingale adapted to the filtration Ftis a stochastic integral with respect to Brownian motion B.Supposing that F∈L2(Ω;ν),there exists a Ft-predictable process η such that

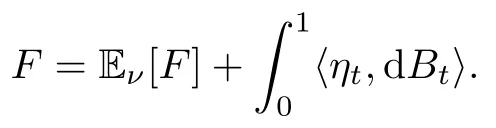
The following theorem gives the explicit form of η for the fractional Ornstein-Uhlenbeck measure:

Theorem 4.1Suppose that F∈Dom(D).There exists a L2(ν×dt)-integrable and Ft-predictable process(ηt)0≤t≤1such that

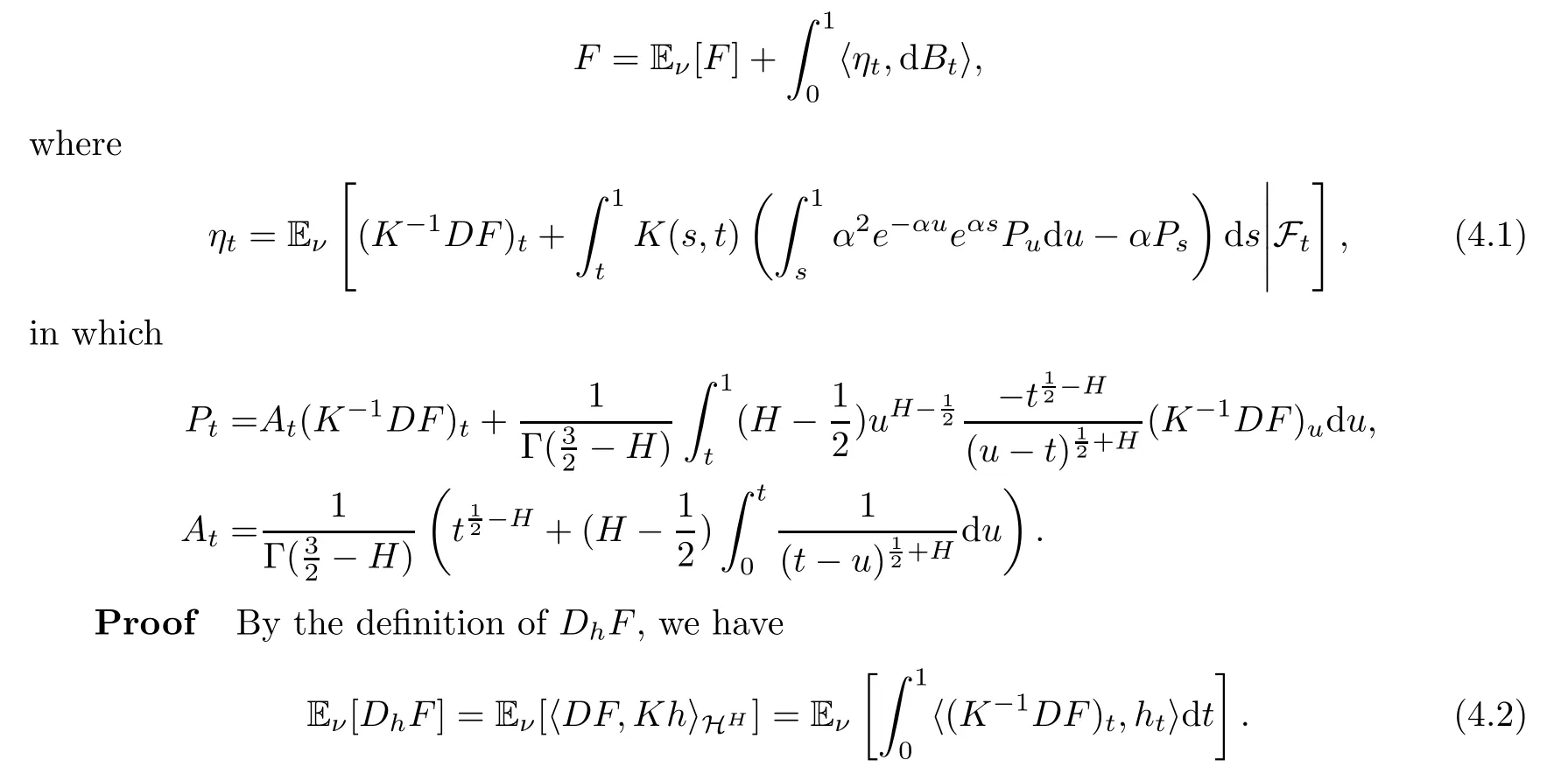
At the same time,by the integration by parts formula(3.4),it holds that

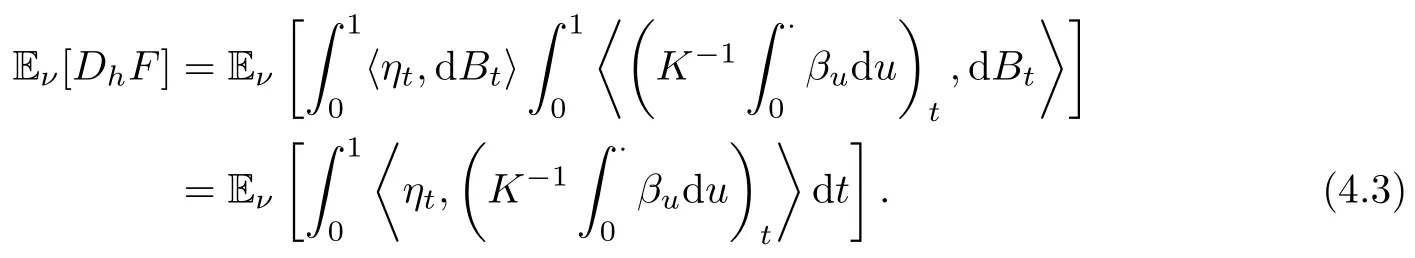
Let

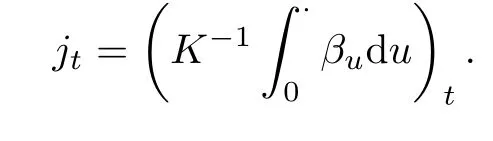
Then,

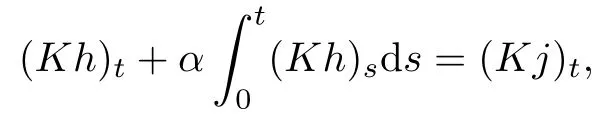
which implies that

Thus

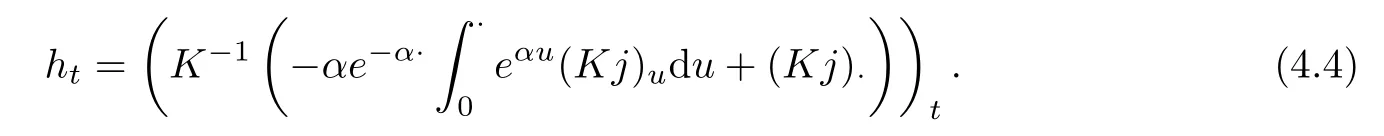
Combining(4.2),(4.3)and(4.4),we have

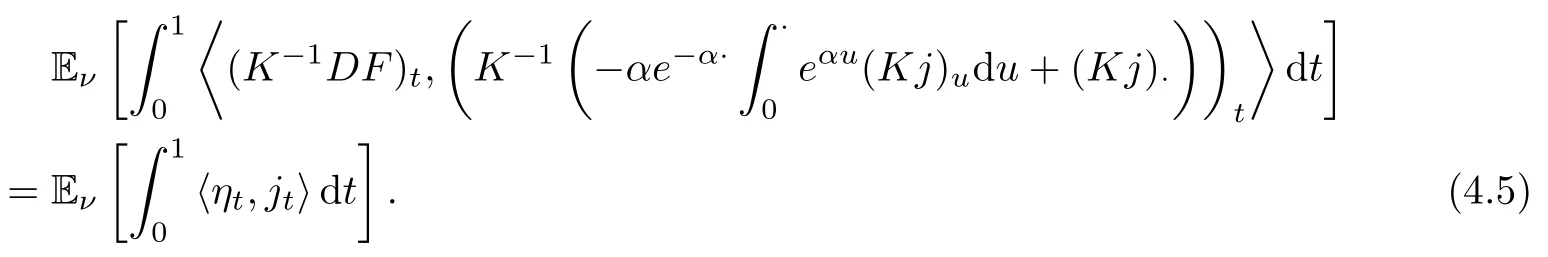
By(2.3)and the linearity of K−1,

where

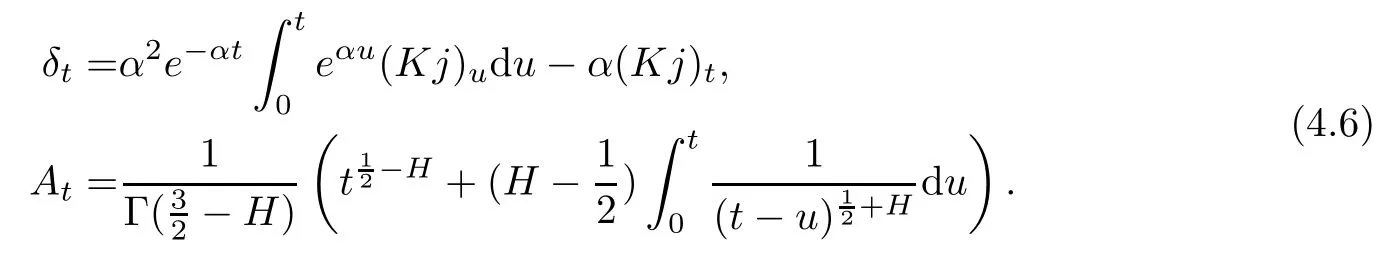
Hence,the left side of(4.5)can be written as

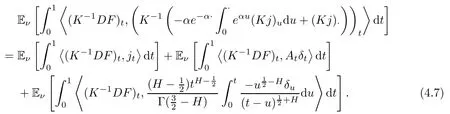
By calculation,the third term of the above equation is

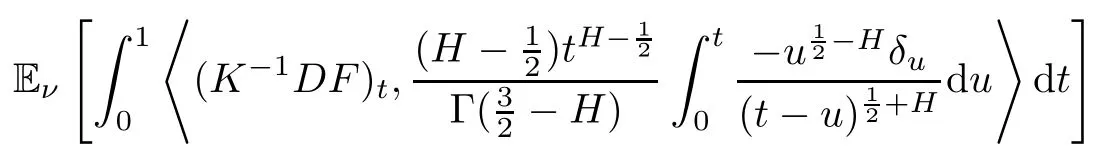
Then(4.7)equals

where

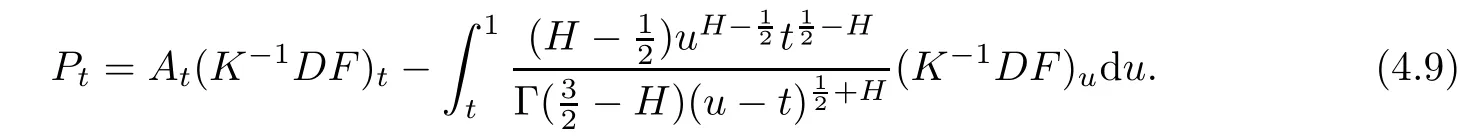
By(4.6),we infer that

Combining(4.5),(4.8)and(4.10),we obtain

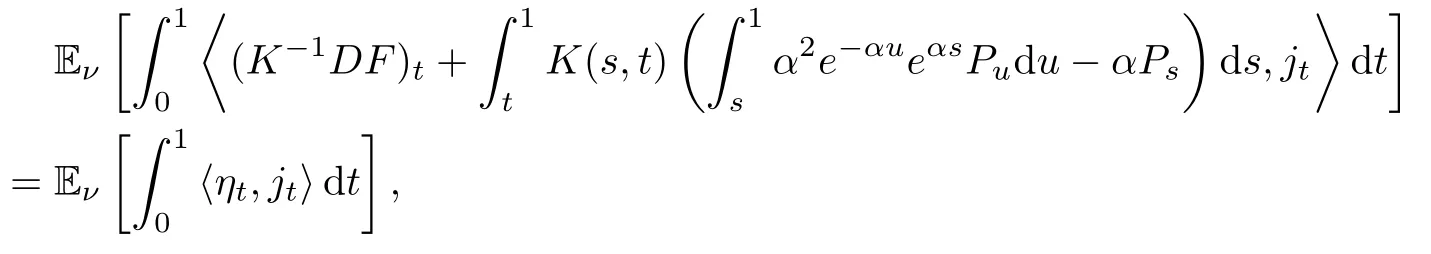
which implies that

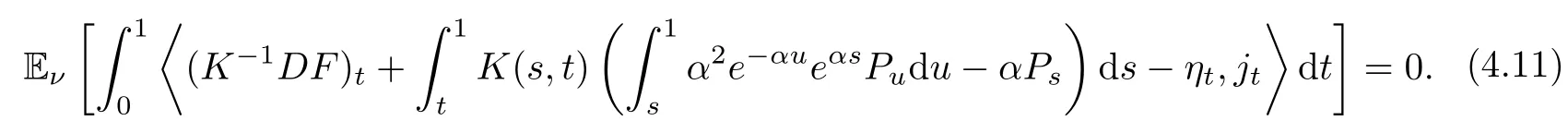
Note that the(Ft)-predictable projection of the process

is

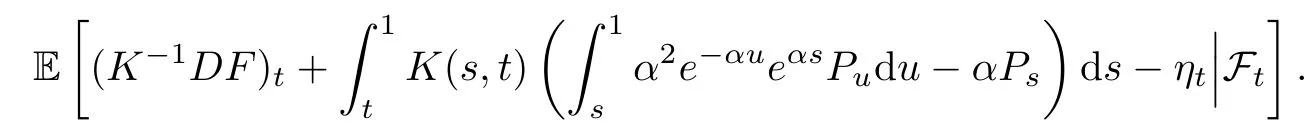
In what follows,we show that

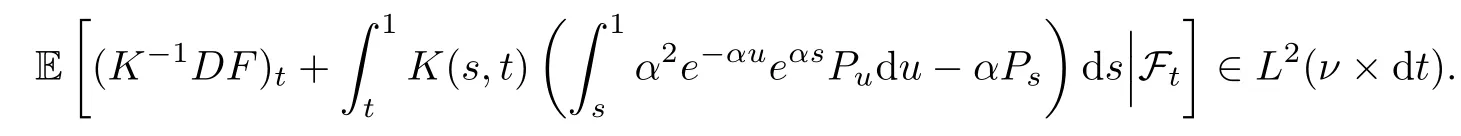
By the Hölder inequality and the inequality(a+b)2≤2a2+2b2,we get

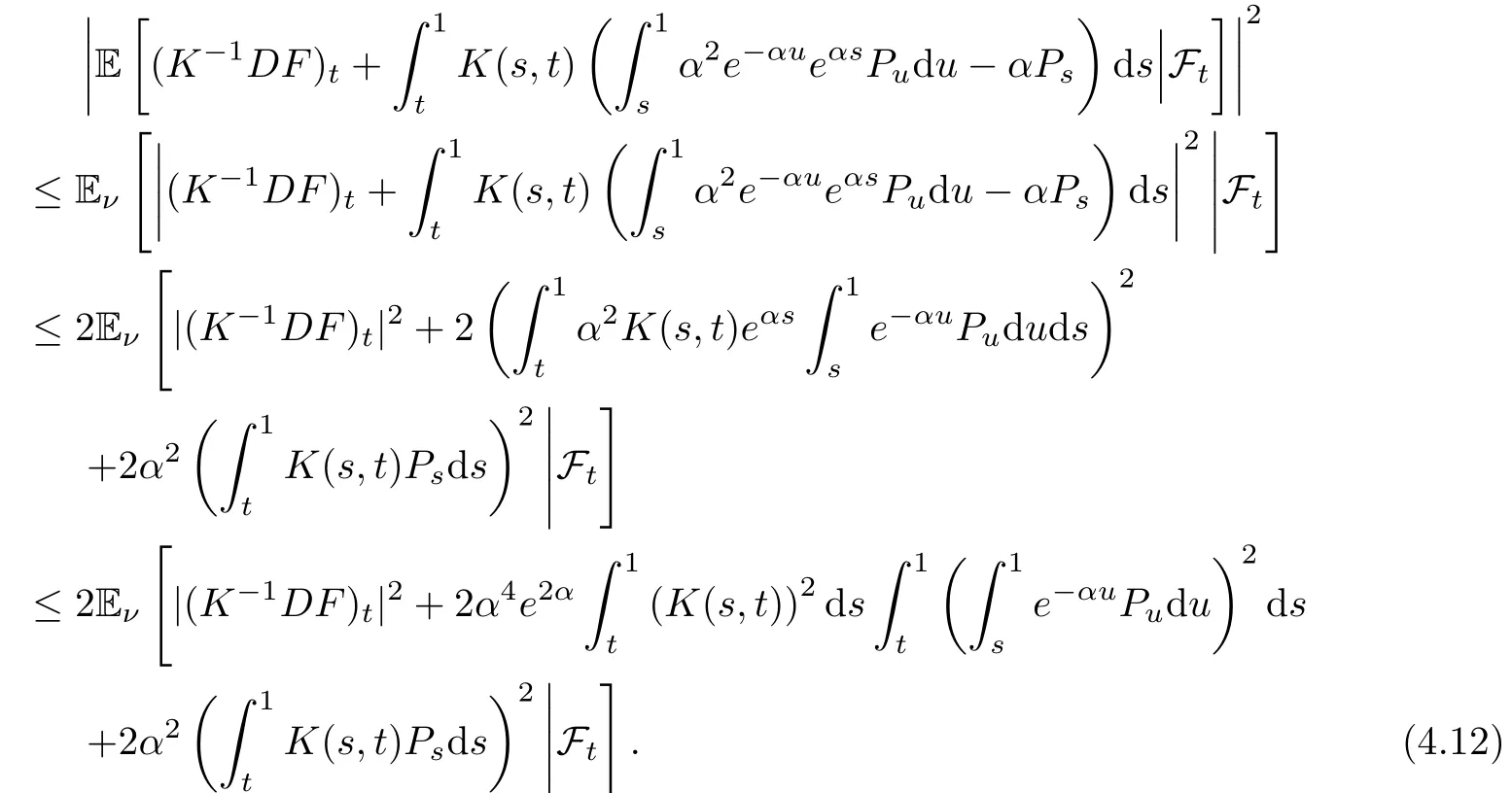
It is obvious that

Hence,by(3.7),(4.12)and(4.13),we gain that

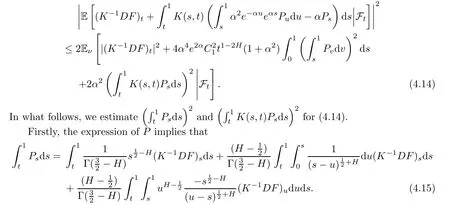
It is obvious that

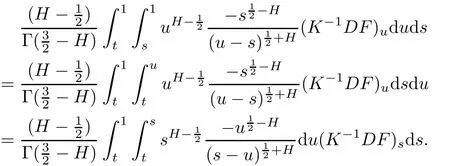
Then(4.15)becomes

It holds that

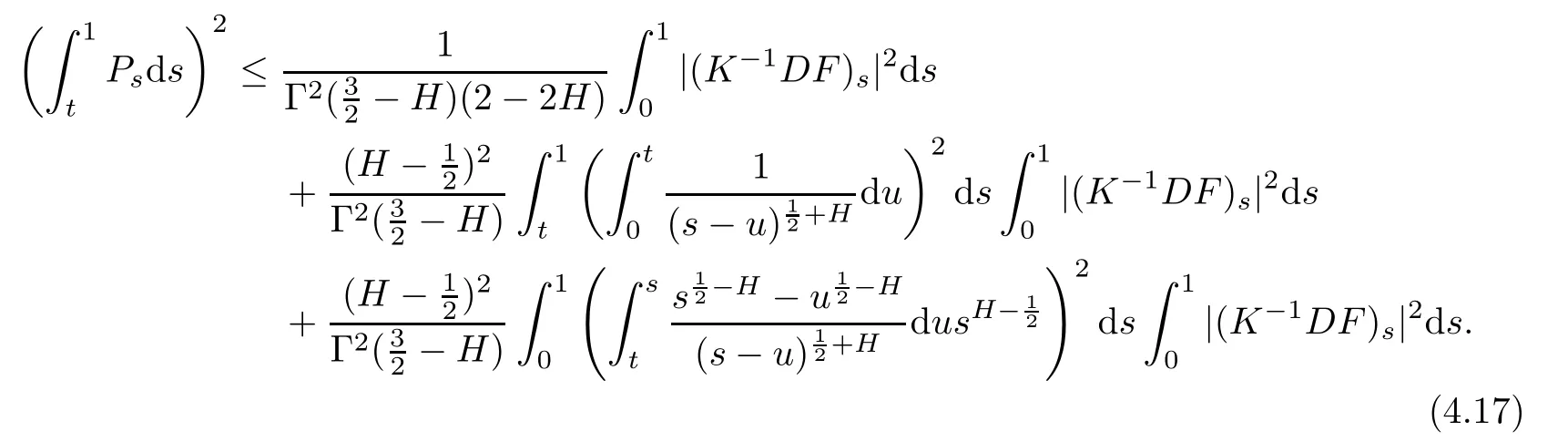
Since

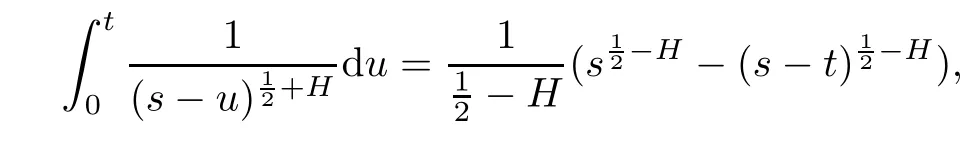
we get

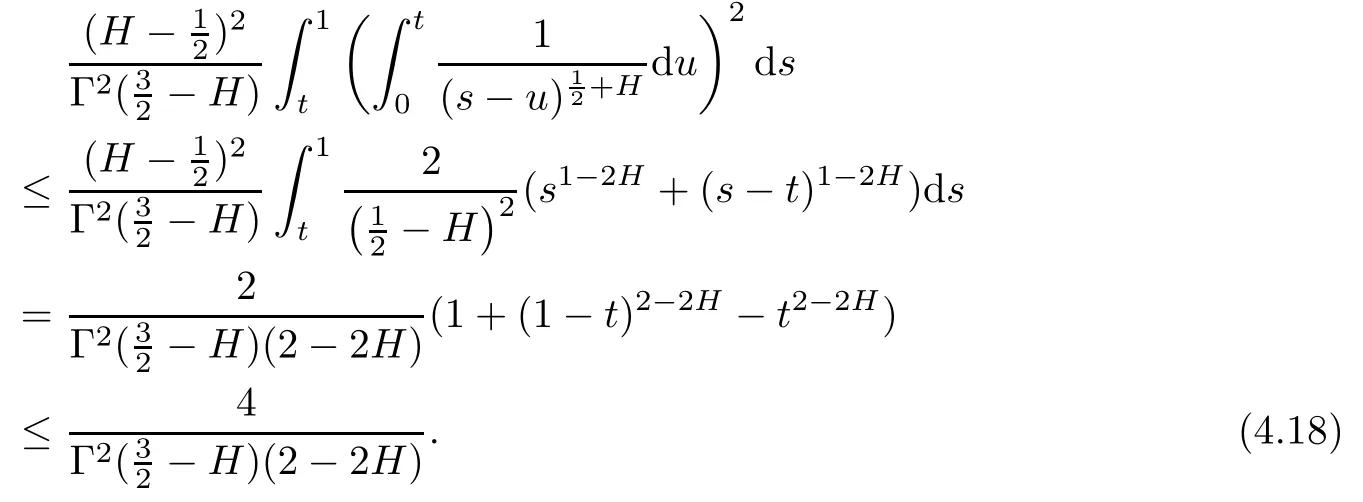
By(3.9),we obtain

Combining(4.17),(4.18)and(4.19),it holds that

where

Secondly,by(4.9),we have

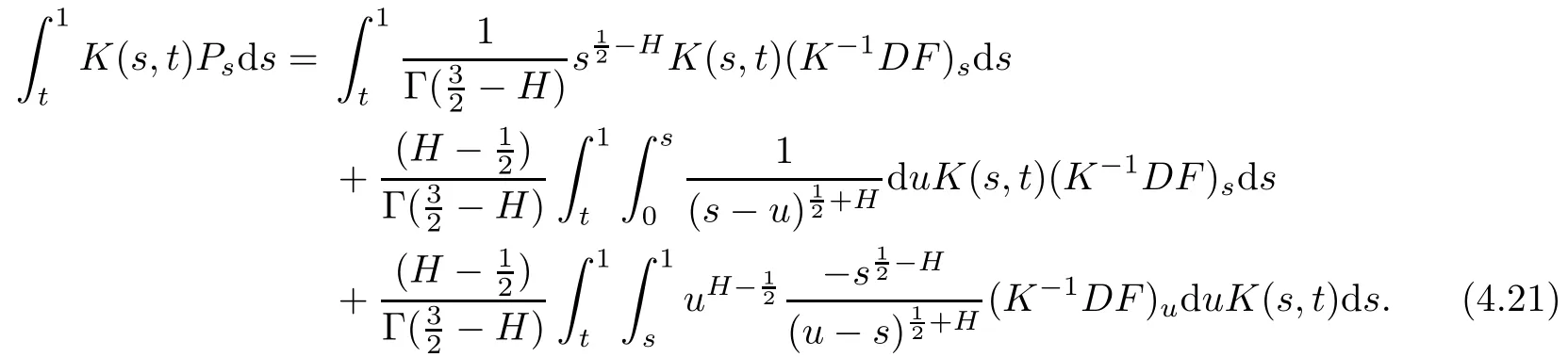
It is obvious that

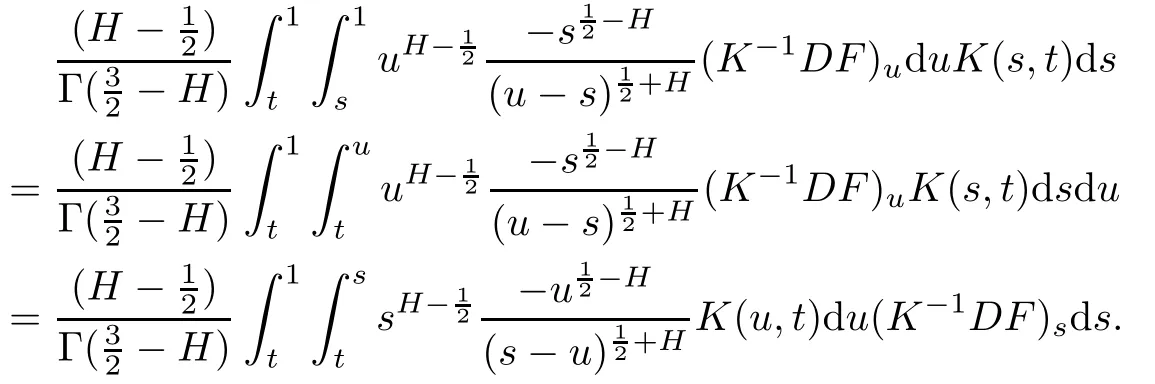
Hence,by(4.21),

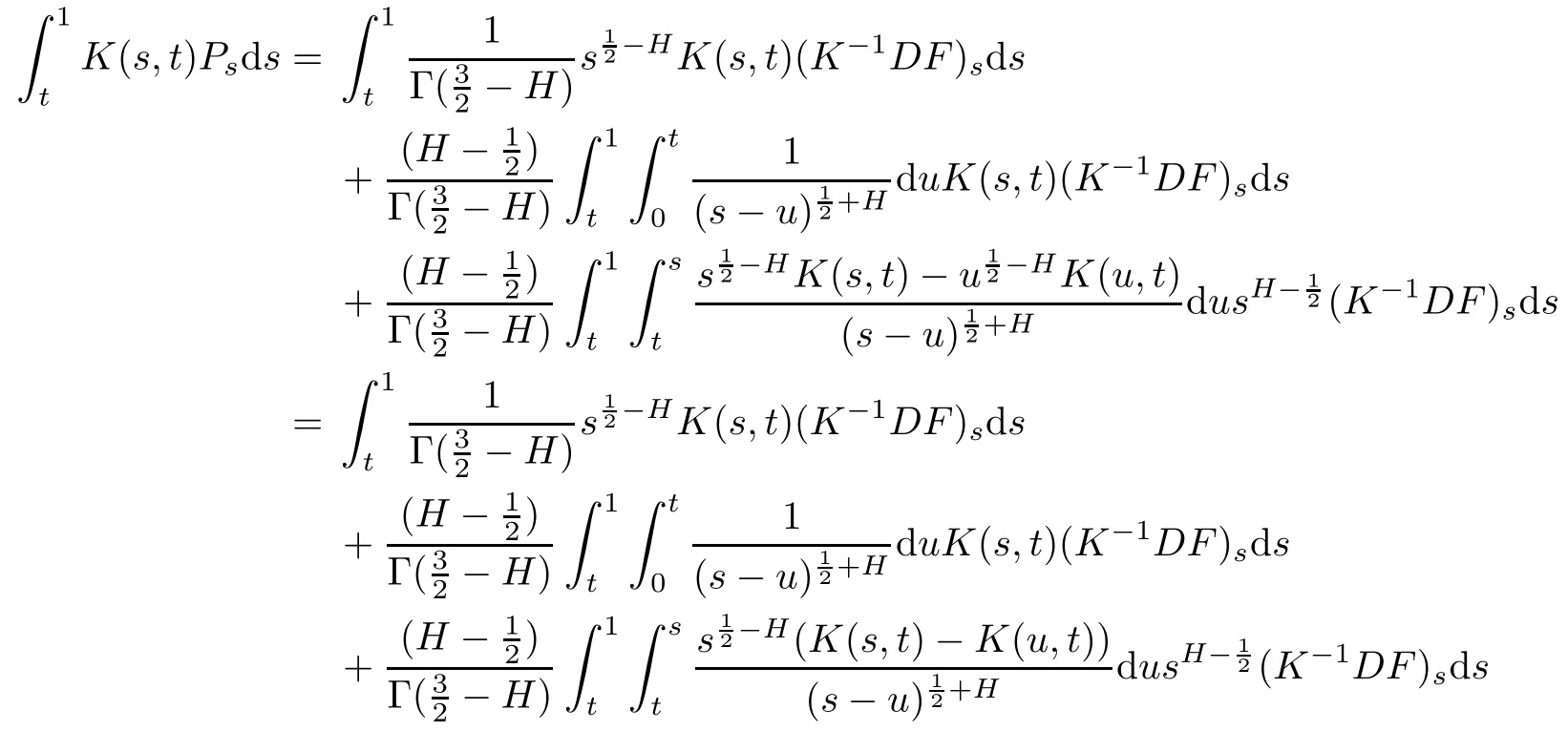
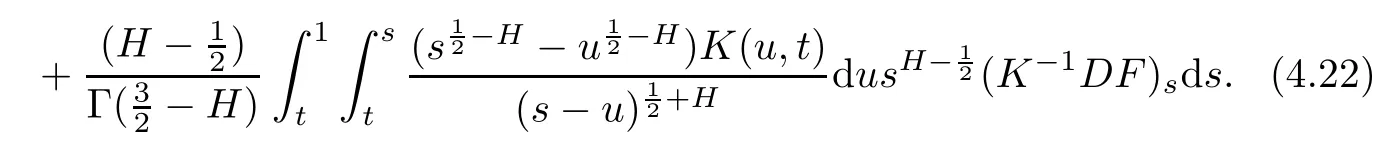
Then,by Hölder’s inequality,we get

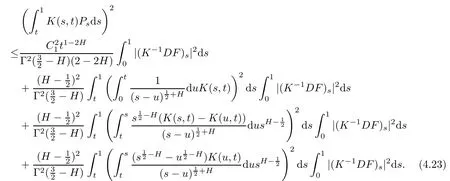
In a fashion similar to(4.18),it holds that

By the expression of K(s,t)in(2.1),we have

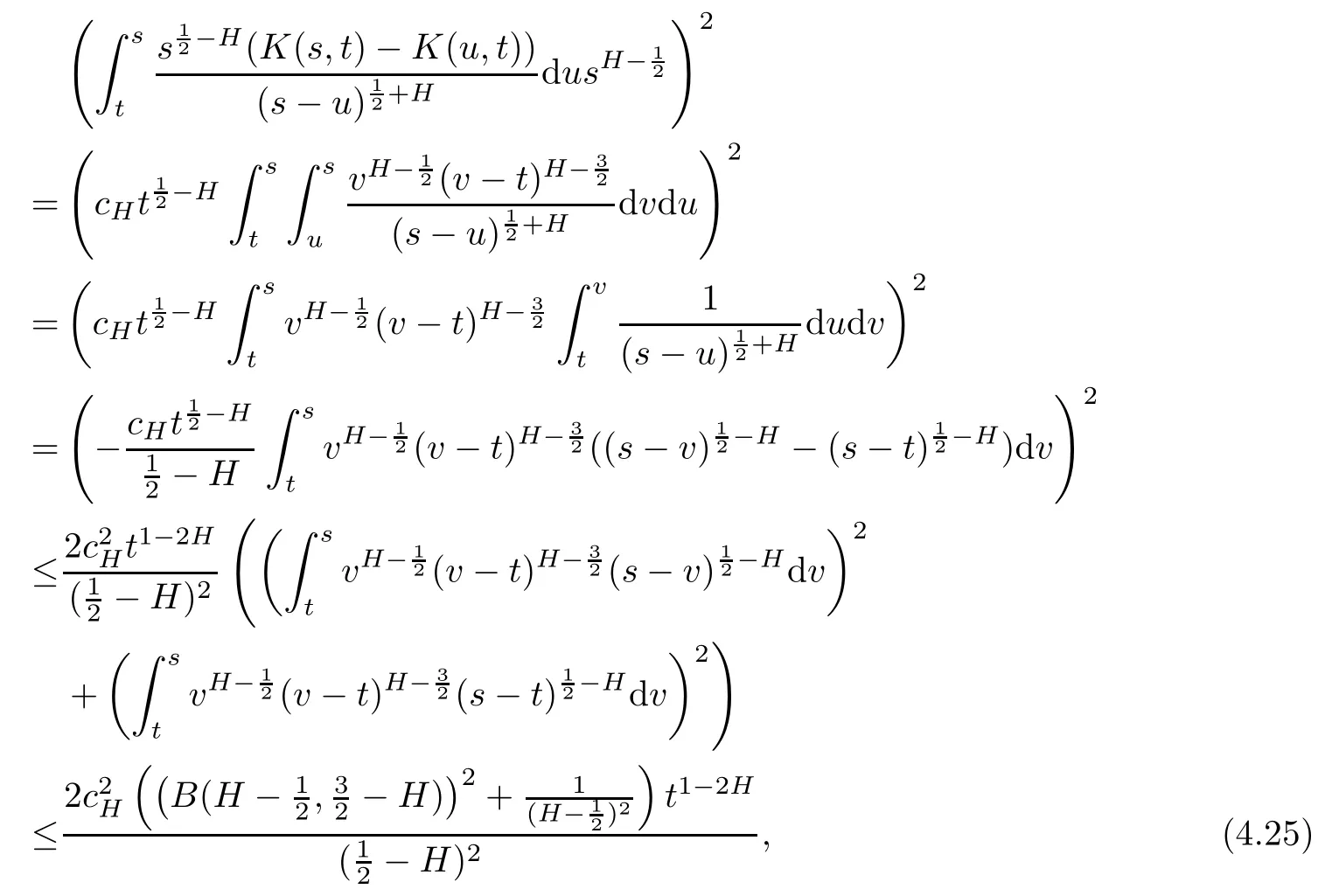
where B(·,·)is a beta function.By(3.7)and(3.9),

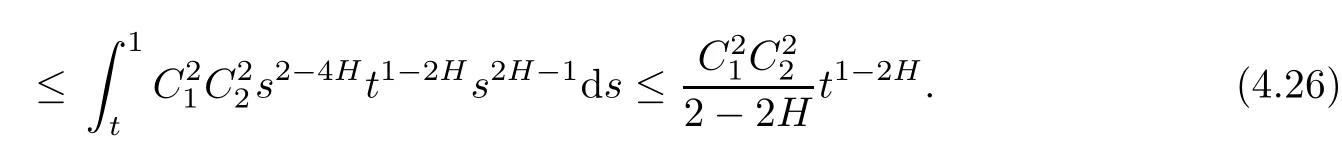
Then,combining(4.23),(4.24),(4.25)and(4.26)yields that

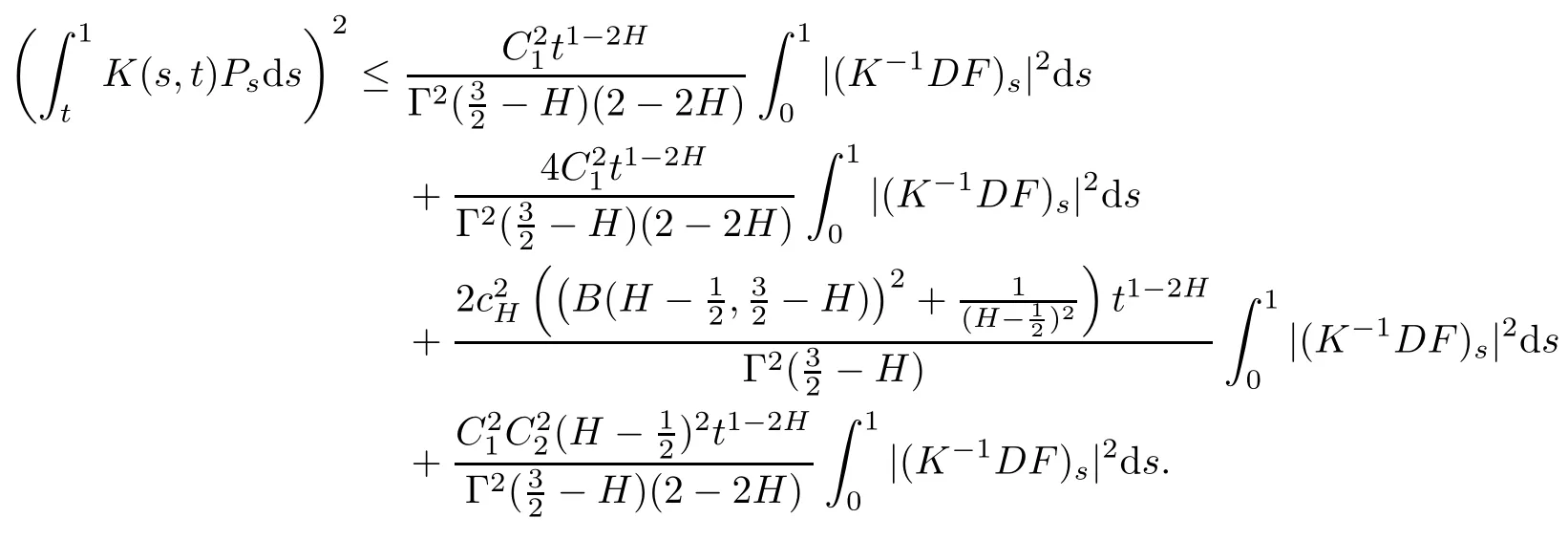
It follows that

where

Therefore,by(4.14),(4.20)and(4.27),

Thus,we obtain

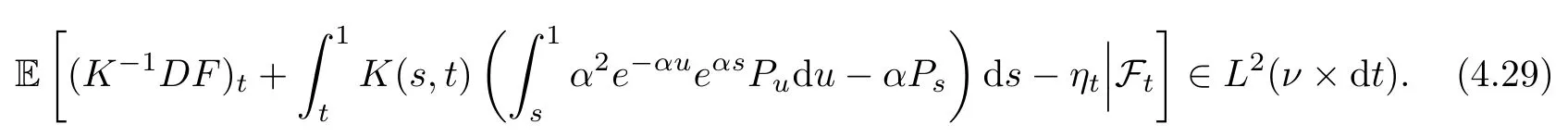
Note that any L2(ν×dt)-integrable and(Ft)-predictable process can be approximated w.r.t.the L2(ν×dt)norm by processes j∈H.Hence,by(4.29)and(4.11),we have

which implies that

Here ends the proof. □

In the following we establish the Logarithmic-Sobolev inequality by the Martingale Representation Theorem in Theorem 4.1:

Theorem 4.2For F∈Dom(D),it holds that

with C1and C2satisfying(3.7)and(3.9),respectively.

ProofLet G=F2and let Gtbe a right continuous version of Eν[G|Ft].Then,by Theorem 4.1,

where η satisfies(4.1),in which F is replaced by G.By Itô’s formula,we obtain

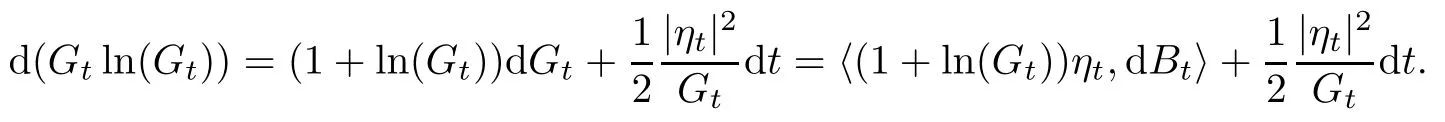
Due to G1=Eν[G|F1]=G and G0=Eν[G|F0]=Eν[G],we get

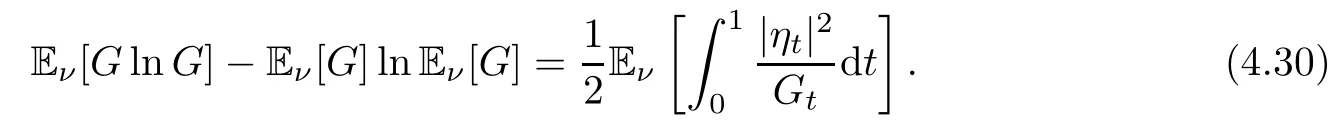
Since DF2=2FDF,it holds that

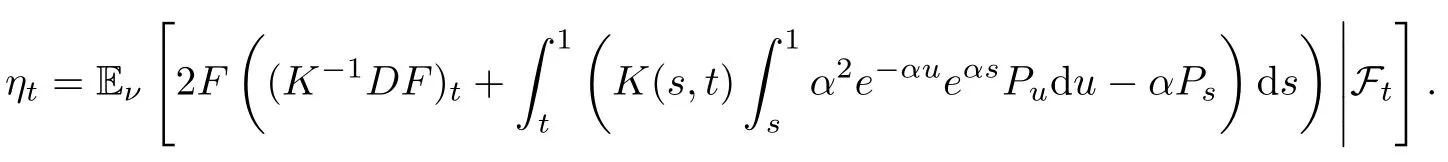
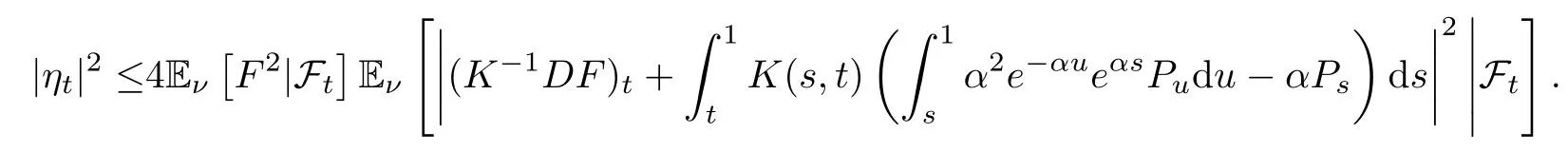
Then,by(4.28),we have

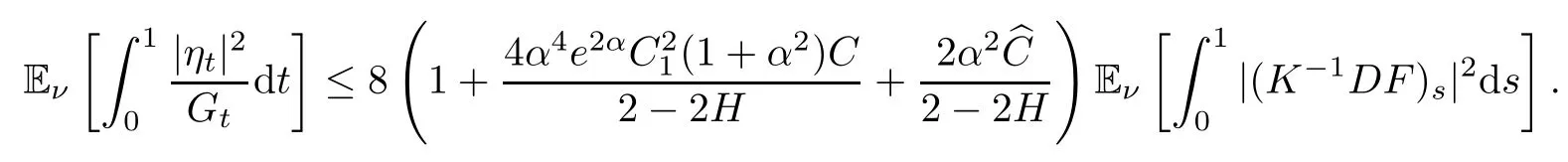
Hence,by(4.30),we obtain the Logarithmic-Sobolev inequality

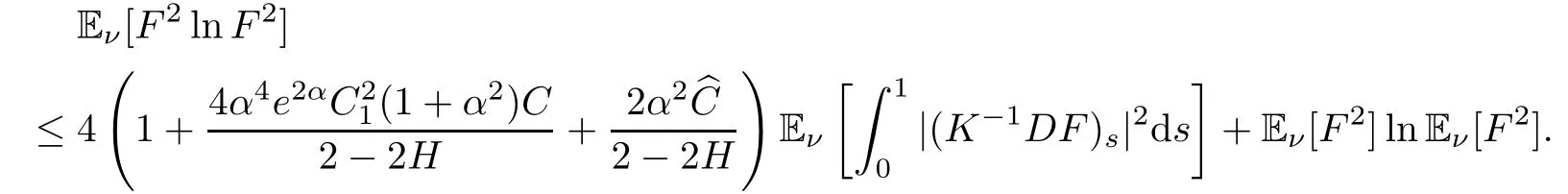
This completes the proof. □

Remark 4.3We should point out that the Logarithmic-Sobolev inequality for ν in Theorem 4.2 can be deduced directly from a Gross’s logarithmic Sobolev inequality in[18,Theorem 8.6.1],since such inequalities are dimension free.The proof given in this paper can be seen as an application for the Martingale Representation Theorem in Theorem 4.1 and this idea is useful when we consider the Logarithmic-Sobolev inequality for the fractional Brownian motion over a Riemannian manifold(c.f.[18,Theorem 8.7.1]and[12,Theorem 5.2]).