一种减少网络振动的智能路由选择算法设计
邵天竺 王晓亮 陈文龙 唐晓岚 徐 敏
(首都师范大学信息工程学院 北京 100048)
(nestea_god@hotmail.com)
近年来互联网和移动通信产业的快速发展,网络系统不断向着规模化、异构化、动态化的方向演进[1].同时,伴随着5G网络的成熟,万物互联将带来网络终端数量、网络流量以及应用形式上的新一轮爆发性增长,并对数据转发速率、超低延迟、高能效比和大规模连接提出更高的要求[2].由此带来的服务能力和复杂性问题使得当前的网络系统面临无数新的挑战,现有尽力而为的路由转发算法难以满足这些应用所带来的多样化的网络服务质量需求.
随着网络环境的不断发展,当面对突发流量或大流量时,基于最短路径的传统路由协议可能导致严重的网络拥塞.互联网需要一种更加智能的路由策略,将网络状态与路由策略融合,提升网络服务质量.然而互联网庞大的网络规模和数据流量使得智能机制的设计充满挑战.
机器学习技术近来已取得高速发展,在计算机网络方面,有监督和无监督的人工神经网络(ANN)技术从路由策略到入侵检测的各种领域中得到广泛应用.尽管传统的浅层人工神经网络经常被用于主动网络管理的流量预测,然而其性能实际上是相对受限的[3],因为单纯增加ANN的隐藏层数量难以改善网络操作决策(例如调度、路由等)的性能.然而,深度学习系统(例如Deep Belief Networks,Deep ANNs和Deep Boltzmann)的快速发展给网络领域的研究提供了新的突破点,它的算法性能显著提高[4].
以深度学习技术为基础的智能路由算法设计,其核心思想是利用大数据驱动的网络特征获取机制,从部署范围的历史数据中寻找路由选择与时间、或路由选择与流量间的映射关系,从而指导后续路由优化.
相比传统数学模型支持下的路由策略设计,数据驱动的智能路由算法具有复杂度低和通用性强等优势.其中,复杂度低主要体现在其避免了针对网络复杂特性和多样需求的数学建模工作,以历史流量数据为基础,通过神经网络的迭代训练代替精确建模,大幅降低核心映射的获取复杂度;通用性强则体现在相同的机器学习模型,可以面向不同的网络环境和需求场景,采用不同的数据集来求解对应的差异化问题.
然而,随着智能化路由技术的发展,新的技术挑战也随之而来.通过实验我们发现,目前的智能路由算法在基于历史数据进行路由更新时,很容易因为局部流量的微小变动而导致大范围的、无关流量的调整,在每个调整周期造成大范围的链接断连、丢包以及路径切换,对网络传输性能带来了负面影响.显然,这是智能路由算法迫切需要优化的问题.
本文中,我们提出了一种对路由抖动敏感的智能路由调度算法FSR(flap suppression routing).FSR的核心思想是在实现全网链路负载均匀分配、最大化利用全网转发资源的同时,寻求与当前路由选择变动最小的更新方案,使得每个更新周期带来的路由抖动尽可能小,路由快速收敛,提升网络整体转发效率.实验发现,FSR算法能够明显提升路由收敛速度,与对照算法相比提升约30%的网络吞吐量,并显著减少网络丢包和链路拥塞.
1 问题描述
路由选择是互联网网络层的核心机制,稳定而高效的路由选择可以保障一个网络系统良好的运行.传统路由协议的核心建立在最短路径的选择上,而并未考虑网络当前的负载分布和未来可能的流量分布情况,所以传统路由面对复杂网络状态特别是突发流量的情况下容易造成网络拥塞.如图1(a)左图所示,在节点A和节点B之间的链路由于突发流量造成拥塞时,基于最短路径的路由算法无法有效避让.更令人失望的是,由于传统路由选择算法不具备从历史流量分布中学习规律的能力,所以造成的拥塞情况在流量规律性很强的场景下会反复发生,严重降低网络使用体验.
因此,设计一种新型的智能化路由策略是网络发展的迫切要求.它应融合网络当前状态信息,从网络的历史行为中寻找规律,进行智能化路由选择,提升网络运行效率,实现如图1(a)右图所示的效果.目前,已有一些相关工作利用深度学习进行路由选择.其中,算法LRD[5]提出了独特的流量矩阵,将流量矩阵作为深度学习的特征输入,并且在最大化链路利用率的问题上给出了较好的解决方案.算法RDL[6]则首次将CNN神经网络应用在流量工程上,与LRD不同的是,RDL以流量需求矩阵做为特征输入,对于突发性流量具有更好的适应性.
然而,经过实验研究发现,目前智能路由算法仍然存在进一步改进的空间.由于目前的智能路由算法主要是学习历史流量的分布特征与路由选择直接的映射关系,并将其应用到当前流量环境的路由选择问题中,所以当网络流量分布发生变化时,很容易引起较大范围的路由抖动.如图1(b)左图所示,预期节点D和节点B间链路可用性降低时,原本仅需调整数据流2即可,即将数据流2的转发路径调整为A—B链路.但由于当前智能路由算法尚未考虑路由振动,故无关的转发路径1也受到影响,重新进行了选路,这无疑会影响整个网络的传输效率.
我们在NS3仿真平台上设计了一个18条链路构成的拓扑,对该网络重放30 min的测试流量并每5 min重构网络路由,并观察3个重构周期,结果如表1所示:

Table 1 Impact of Oscillation Caused by Route Reconfiguration on Network Transmission表1 路由重构引起的振动对网络传输的影响
RDL算法平均每次路由更新都会导致约9.7条链路受到影响,比例达到50%以上,而受到影响的完整转发路径达到4.7条.LRD算法相类似,在同样实验条件下,它会导致约12条链路受到影响,比例达到约70%,受影响的转发路径达到5条.这无疑会影响整体网络的转发性能.在300 Mbps带宽的链路上,RDL和LRD算法分别取得的平均带宽为229.93 Mbps和234.43 Mbps.其中,在第1个路由更新周期调整完成后,2种算法取得的平均带宽均受到严重影响,分别下降到176 Mbps和135 Mbps,只能达到最大带宽的58.67%和45%,传输效率受到显著影响.
于是,针对这一问题,本文提出了一种振动抑制的智能路由选择算法FSR,在图1(b)右图所示的情况下,仅调整受D—B链路影响的数据流2,将因此带来的路由抖动收敛到最小状态,进而提升网络传输效率.由此,保证尽可能少的改动网络路由选择,同时提升网络资源的利用率.
2 FSR算法设计
不同于现有研究工作,FSR需要关注转发路径的变化,尽可能抑制端到端路由抖动,其主要设计思路有2个特征:
1)在挖掘历史流量的特征信息时,不满足于传统机制对链路状态与时间关联规律的探寻,而是寻找路径-链路-时间3个维度的变化特征.本文设计了如图2所示的模型结构,通过链路、路径2个维度构建流量矩阵,再增加时间通道刻画二维流量矩阵的时间变化特性.以此做为输入数据,使得训练得到的神经网络可以更加全面地刻画流量特征,从而寻找路由动荡最小的全局路由方案.
2)本算法针对不同的网络规模,其输入矩阵也存在较大差异.
考虑到随输入参数增加而可能出现的梯度消失或梯度爆炸问题,FSR算法选择具备卷积层的CNN神经网络以更好地适应不同规模的网络输入.
因此,本节将从算法的优化目标入手,着重研究FSR算法的输入输出处理和CNN神经网络设计,以此为基础完成抖动抑制算法的设计和实现.
FSR算法中的CNN网络结构如图2所示.整体结构由卷积层、池化层和全连接层构成,每一层的参数说明为:
第1层(L1).该层为输入层,每个输入样本为10@30×18的输入矩阵,其中10代表共有10个时间采集点,30为整个网络中有30条链路,18表示18个OD对.
第2层(C2).该层为卷积层,主要作用是对原始输入样本进行空间滤波,因此该层与输入层之间的连接是局部连接.在该层使用15种滤波器,每种滤波器去卷积输入矩阵就得到不同特征的映射,即得到15个特征图.卷积核的大小设置为2×2,每个特征图的大小为16×16.
第3层(P3).该层为池化层,主要作用是减少模型特征提取方面的误差.我们设置2×2的池化窗口,采用最大池化的方式对上一层数据进行池化操作.
第4层(F4).该层为卷积层,作用与第2层(C2)相同,在该层使用20种滤波器,每种滤波器去卷积输入矩阵就得到不同特征的映射,即得到20个特征图.卷积核的大小设置为2×2,每个特征图的大小为16×16.
第5层(H5).该层为池化层,参数与第3层(P3)相同.
第6层(O6)与第7层(B7).这2层为全连接层(第3隐含层),作用是配合前面的卷积层和后面的输出层,组成分类部分,因此该层前后都是全连接.神经元个数分别为60个和30个.
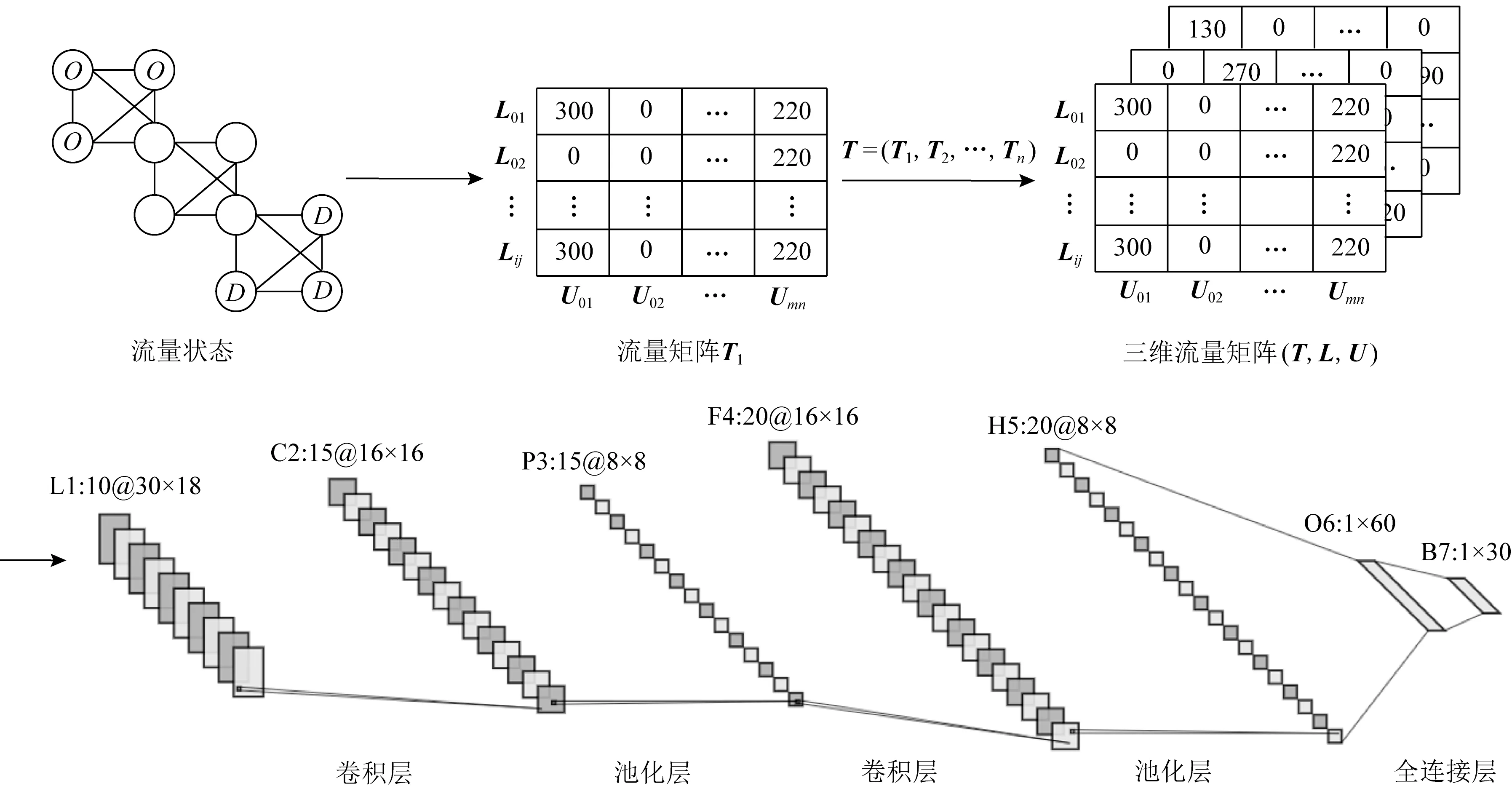
Fig.2 Data processing and neural network design图2 数据处理与神经网络设计
2.1 设计目标
考虑到当前智能路由算法可能带来的路由抖动问题,本文的优化目前将以全网流量的均匀分布作为约束条件,以最小化相邻时间片的路由选择为优化目标,设计整体智能路由算法.
具体来说,令一个网络拓扑表示为无向图G=

为了求解这一优化问题,FSR算法将采用深度学习算法得到满足Max(Load e)<K约束条件的可行解范围,之后在可行解范围内求解链路改变最小的最优解.
2.2 输入输出
FSR算法中,满足约束条件的可行解范围由CNN深度学习神经网络给出.针对CNN神经网络,本节首先讨论算法的数据初始化处理.
区别于传统流量工程中对网络流量的矩阵描述,本文中所设计的流量矩阵,同时包含路径和链路的流量分布状态,在横向和纵向2个维度的特征关联性更强,这有助于CNN的卷积层更好地获取这2个维度间的关联特征.我们还在输入上设计了时间通道,使整个数据集更加具有时间连续上的特征.
为了描述网络历史流量特征,FSR算法采用如图2所示的三维矩阵(T,L,U)作为算法输入.其中,T=(T b,T b-1,…,T b-h+1)为历史流量数据的时间片;L=(L01,L02,…,L ij)表示节点i到节点j间的链路上的流量;U=(U01,U02,…,U mn)表示节点m到节点n的完整路径上的流量.对矩阵中某一行求和,可以得知所有通过该链路的传输路径的总流量.而观察某一列的非空项,则可以得知该时间片内此源—目的(OD)对间的路径所包含的链路,横坐标代表了路径情况,而纵坐标表示链路情况.我们对于不同的路由拓扑输入的矩阵大小是不同的,所以对于一旦处理维度较大的输入矩阵时,ANN的训练参数会急剧增加,容易出现梯度消失或爆炸的现象.而在前面加上了卷积层的CNN能更好地去适应不同的路由拓扑.
训练数据采集自MAWI Working Group Traffic Archive所提供的WIDE到上游ISP的传输链路上的跟踪流量.首先,将网络总体流量数据按照时间片分割为流量序列,这里时间片长度可以任意指定,时间片长度为5 min.之后,将该流量序列输入到提前构建好的网络拓扑中(网络拓扑具体形式参加第4节实验部分),按照OSPF协议进行该流量序列的路由转发,并以30s的间隔观察网络流量分布情况,对于任意链路的负载Load e>K的情况,剔除该流量分布数据,将剩余的所有流量分布情况做为训练数据使用.将训练数据转化为网络流量特征矩阵的形式则可得到最终的训练集DataSettrain.
FSR算法中,CNN输出的结果是当前流量分布情况下的可行解范围,具体的形式是针对每一个OD对,给出其可行路径方案的概率值.FSR算法是去解决一个多分类的问题,于是本方案不仅为最终的结果进行了标签的标注,同时为每一个OD对的路径进行了序号的标注,于是可以准确地通过标签来反映出拓扑路径的选择.
首先,需要在算法运行之前,针对每一个OD对,给出其可选的路径方案集合Path,为了控制神经网络算法的可行解空间,FSR算法需要对Path集合进行预处理,设每个源—目的对间的可行路径数量上限为n,于是,对于给定的网络拓扑G=
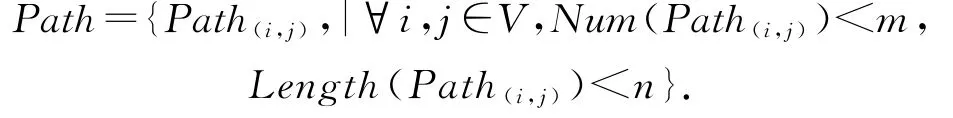
FSR算法中CNN在此基础上,针对每一个OD对(i,j),输出其Path集合中每一条路径的选择概率p,即CNN的输出为

之后,FSR算法在CNN的输出集中,按照选择概率p降序排列,并计算每一个路径方案Path(i,j)所对应的链路抖动幅度,最终将抖动幅度最小的方案做为FSR算法的输出,进行下一时间片的路由调整.
2.3 神经网络设计
CNN神经网络中的神经元采用ReLU激活函数,具体形式为

CNN神经网络中,卷积层的正向传播函数为
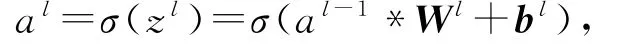
其中,a l为第l层神经元的输出,z l为第l层神经元的输入,W l为从l-1层映射到l层的权值矩阵,b l为与上面参数对应的偏移值,σ为激活函数ReLU.另外,FSR中采用均方差来度量损失值,对应的损失函数可为
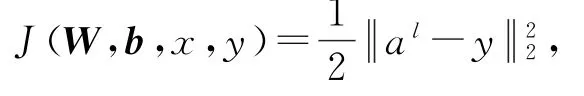
其中,x为训练集输入,y为训练集中期望的输出结果.
按照CNN神经网络的基本思想我们给出全连接层也就是DNN神经网络正向传播的公式:
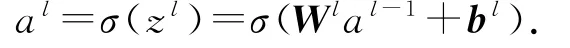
根据随机梯度下降法可以给出全连接反向传播公式:
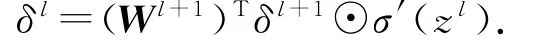
算法1.CNN全连接层算法.
输入:最大迭代次数Max、学习率α、输入的样本对{(x1,y1),(x2,y2),…,(x m,y m)};
输出:各层的W,b.

阈值,就跳出循环输出各层的W,b结束∗/针对池化层,本文采用的是最大池化(max pooling)的方法,设置大小为2×2的池化窗口来减少模型特征提取方面的误差,这一误差主要来自2个方面:1)邻域大小受限造成的估计值方差增大;2)卷积层参数误差造成的估计均值偏移.
结合上文给出的卷积层正向传播函数可以得到池化层输出的反向传播函数:
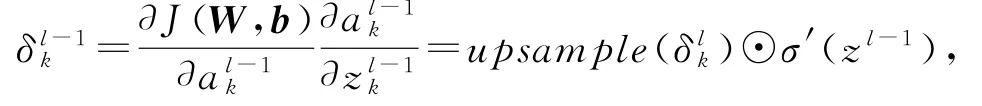
其中,upsample操作为最大池化的过程.
CNN神经网络中的所有权重都用随机函数初始化,即高斯函数和Xavier函数.利用训练集不断优化权重设置,直到获得CNN神经网络合理的权重矩阵.
训练阶段,FSR算法把训练集输入上述CNN网络中,不断地进行迭代计算来自动地调整模型参数.同时,在训练中采用了10重交叉验证(10-fold cross-validation)的方式,这样可以有效地避免陷入局部优化问题.
在上述神经网络设计的基础上,FSR算法采用如图3所示的结构,利用历史流量数据进行CNN神经网络的训练,完成训练后,FSR算法通过获取实时数据进行流量特征的抓取并输出供优化的备选路由调整方案,通过抖动抑制机制,最终选取路由抖动最小的调整方案,进行下一时间片的路由更新.
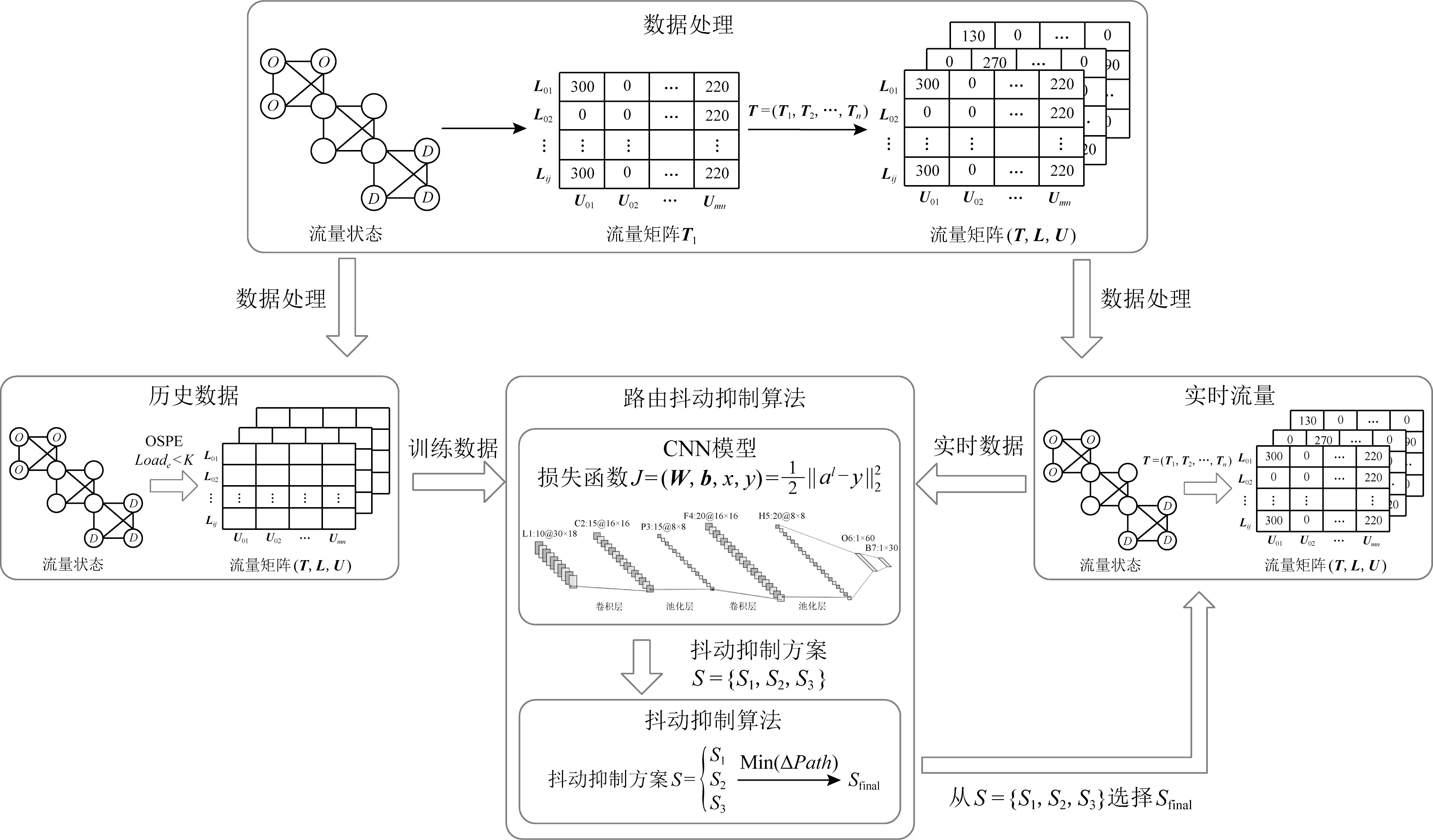
Fig.3 Architecture of FSR algorithm图3 FSR算法架构
2.4 抖动抑制
CNN神经网络会给出下一时间片内可能的流量优化分布方案,但根据第1节讨论过的,这样的流量分布方案可能带来普遍的路由抖动、传输中断、数据重传等问题,进而导致网络整体传输性能下降.于是我们需要在待选方案中,选择尽可能减小网络振动的方案,可能的方法有:
1)最小化路径变动.这是设计上最为简单的方法,我们将主观抹去所有传输路径本身的差异性,仅从路径变动的角度去衡量不同方案带来的网络振动.例如原有传输路径为A—B—C—D,下一时间片给出的方案中,一项为A—E—C—D,另一项为A—E—F—D,那么我们将选择前者,因为它相对于现有传输路径,仅改变了一跳,带来的可能的网络抖动是最小的.这样的处理好处是方法简单、计算开销小、便于大规模部署,不足之处则是忽视了不同路径本身的重要程度.
2)最小化流量变动.这是一个更复杂但更合理的方法.若使用这一方法,则我们不再单纯关注相邻时间片网络传输路径的变化跳数,而是要考虑被调整的路径所对应的总体流量大小.这是由于一条传输路径在相邻时间片内可能存在较大的路径调整,但是该路径上仅有10 MB流量,我们应该认为这对网络性能的影响非常有限.如果一条路径本身调整幅度不大,但该路径上承载了10 GB流量,那么我们有理由相信这对网络的影响远比前者更大.
3)加权的流量变动最小化.在1)2)方法的基础上,如果我们同时考虑流量的大小和优先级,那么我们可以得到一个更加合理但复杂度显著提升的抖动抑制方法.这需要我们更好地权衡算法有效性与算法开销间的平衡,甚至设计专门的机器学习机制来处理算法的复杂性.
于是,综合1)~3)路由抖动的评价思想,我们将路由抖动定义为
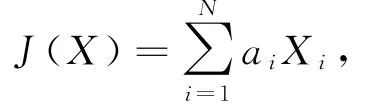
其中,X i表示链路改变数量、改变链路中的负载、改变路径上的时延等可用的输入参数,a i表示X i所对应的权重系数.
本文我们将按照最小化路径变动中的思想,定义备选的路径方案相比上一时刻所最终决定的路径方案中每个OD对改变的链路数量分别为m1,m2,…,m K,其中K为OD对数量.于是,按照最小化路径变动的思想可得到:

在本文中,FSR算法采用第1种最小化路径变动机制来抑制路由抖动,如算法2所示.
算法2.抑制振荡算法.
输入:OD对数量K、每个OD对改变的链路数量m1,m2,…,m K;
输出:改变链路数量最少的路径Jmin.

具体来说,在运行阶段以5 min为一个时间间隔,在每个时间间隔结束时,把当前网络的流量情况整理为网络流量特征矩阵(T,L,U)输入CNN神经网络中.CNN神经网络此时做为拥塞控制模型最终将提供可行路径方案的概率集合OutputCNN,将此集合做为网络振动抑制算法的输入参数,最终FSR算法可以给出当前时刻的最佳路由方案.
2.5 复杂度分析
我们对FSR算法的复杂度进行估算分析.从整体上来看,本文提出的FSR算法是由CNN神经网络以及抑制抖动算法所组成,我们首先来讨论神经网络的复杂度.CNN神经网络的复杂度可以直接按照表达式O(M2×K2×Cin×Cout)获得,其中M为输出特征图(feature map)的尺寸,K为卷积核(kernel)的尺寸,Cin为输入通道数,Cout为输出通道数.输出特征图尺寸又由输入尺寸X、卷积核尺寸K、填充Pad ding、步长Stride这4个参数决定,具体可表示为M=(X-K+2×Pad ding)/Stride+1.对于不同拓扑的输入尺寸的增大,时间复杂度也会随之升高.另一方面,本文提出的抑制振荡算法为最小值的排序算法,抖动抑制算法时间复杂度为O(n),故整体算法的复杂度取决于神经网络的复杂度.
3 实验分析
我们设计了4组实验分别对FSR算法与对照组算法RDL、算法LRD进行了综合的性能对比和实验结果分析.实验内容包括拥塞率、吞吐量、传输路径的平均跳数和算法运行时间.
3.1 实验设计
在本实验中,我们期望FSR算法训练得到的神经网络,能够对网络流量的变化产生恰当的反应,并指导网络中的路由选择以较低的变动成本做出有效响应,使得全网流量合理分摊,所有链路均得到高效利用.
为了验证算法有效性,我们在NS3仿真平台上设计了4组实验,使用的仿真设备硬件配置为:CPU为I7-8700K,GPU为NVIDIA TESLA T4,内存为64 GB,分别从网络拥塞率、网络最大吞吐量、网络的平均路径长度和运行时间这4个方面对算法性能进行了综合的对比与分析评价.另外,由于路由选择与网络拓扑具有相关性,为了验证算法在不同网络拓扑下的性能,构造了4种拓扑结构同时进行实验,如图4所示.
关于本实验中4种不同的拓扑设计,其目的是为了验证在不同节点和可选路由规模的情况下,FSR算法对于网络流量优化及路由抖动抑制的综合效果.FSR算法和当前智能路由算法能够优化网络流量分布的前提,是网络中任意2个节点间存在足够数量的可选路由路径.所以对于结构过于简单、节点间连接不够丰富的拓扑,路由调整空间受限,实验无法分析出智能路由算法与传统路由算法性能上的差别.因此,本实验中,我们按照节点数量逐渐增加,可选路由数量逐渐增加的思路,设计了如图5所示的4种拓扑结构.
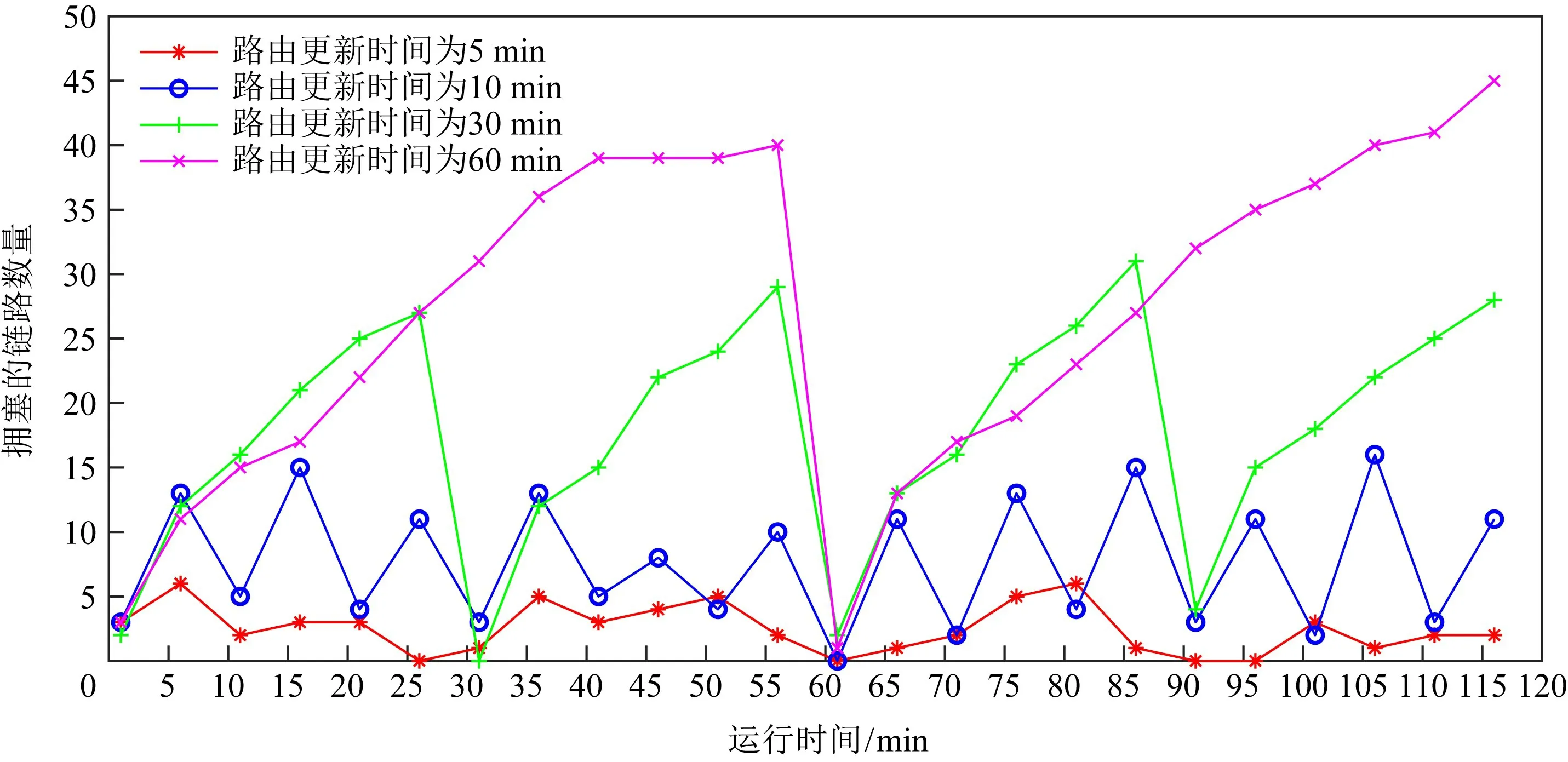
Fig.4 Number of congested links in different time slices图4 不同时间片下拥塞链路数量

Fig.5 Experimental topology图5 实验拓扑
本节实验中使用到的网络流量来自于MAWI Working Group Traffic Archive所提供的WIDE到上游ISP的传输链路上的跟踪流量,时间跨度为2009-03-30—2009-04-06.同时,为了横向对比并验证FSR算法的性能,我们选取了RDL,LRD两种算法.其中,LRD算法在流量工程中将流量矩阵作为深度学习的特征输入,在最大化链路利用率的问题上给出了很好的解决方案.RDL算法则将CNN神经网络应用在流量工程的问题上,并以流量需求矩阵做为特征输入,能适应突发性流量.
3.2 时间片选择
本文我们将路由选择按照时间片进行周期更新.时间片在本实验中具体设定为5 min.关于时间片的取值,其实质是网络资源充分利用与路由稳定性间的平衡问题.我们分别以5 min,10 min,30 min,60 min作为路由重构的时间片选择,使用拓扑4的网络环境,以2 000 Mbps生成速率在120 min内统计拥塞链路的数量,实验结果如图4所示.可以看出,时间片间隔越长,路由稳定性越好,对于网络连接的影响越小,但是另一方面,时间片间隔越长,由于路由灵活性降低,网络中出现链路利用率不均的情况越来越验证,造成网络中链路拥塞的数量越来越大.所以得出时间片的选取将是针对不同网络环境进行资源利用率和路由稳定性间的权衡取舍,在本实验中,5 min的时间间隔是我们在实验中挑选的一个实践数值,该数值在我们设置的网络环境中能够较好地平衡网络流量分配和传输稳定性,并证明本文提出方案的有效性.
3.3 实验结果分析
本节将详细讨论每一组实验的具体设计和实验结果,并对实验结果进行详细分析和讨论.实验结果显示FSR算法在得到的网络性能上全方面优于对照算法组,证明FSR算法有效抑制了路由重构时带来的网络性能下降,与对照算法相比提升约30%的网络吞吐量,同时显著降低路径长度和拥塞概率.
3.3.1 拥塞率
本实验考察各算法在网络流量不断增加的情况下,能否利用网络现有带宽资源,保障网络通信效率,尽可能减少网络拥塞.
在图5所述的4个网络拓扑中,分别测试FSR,RDL以及LRD算法在网络流量不断增加的情况下网络拥塞出现的概率.其中网络流量从100 Mbps一直增长到最大3 600 Mbps,直至所有链路均完全拥塞,即拥塞率达到100%为止.在这一过程中,每增加100 Mbps流量分析一次网络拥塞率.在本实验中,我们将网络中某一条链路的利用率大于某个阈值定义为该链路出现了拥塞,统计所有链路中处于拥塞状态的链路占比,作为网络当前的拥塞率.我们得到了如组图6所示的实验结果.
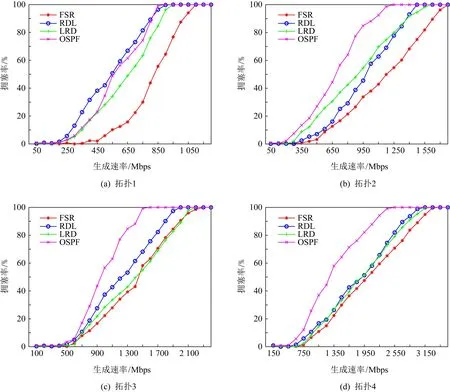
Fig.6 Congestion rate experiment图6 拥塞率实验
FSR在每一种拓扑中,均表现出了最好的网络拥塞抑制能力,说明FSR在不同网络状况下,均具备较为良好的网络资源利用能力.具体来看,在拓扑1中,FSR与对照组算法的差异最为明显,FSR的优势最大.
以全网10%拥塞率为例,对照组算法中,RDL算法在拓扑1中,当源端发出流量达到280 Mpbs左右时,即出现10%的全网拥塞.LRD算法则在相同情况下,当源端流量达到350 Mbps时,出现10%拥塞.OSPF算法与LRD算法相当,相对比来看,FSR算法可以坚持到源端流量达到550 Mbps时,才出现全网10%的拥塞.相比RDL和LRD,FSR算法分别提升96%与57%.再以全网链路全部拥塞出现时的源端流量来看,RDL算法与LRD算法非常接近,均在源端吞吐达到950 Mbps时,全网出现完全拥塞,OSPF算法则在约860 Mbps时出现完全拥塞.FSR算法则可以坚持到源端吞吐达到1 100 Mpbs时才出现全网拥塞.与对照组算法相比,在相同的网络环境下,最大可承受的源端吞吐量提升了16%~28%.由此可见,FSR算法可形成更加合理的路由选择,并更加充分利用全网网络资源,在相同的网络条件下,使得网络可以承担更大的流量压力.
3.3.2 网络吞吐
本实验中,网络源端的流量生成速率从50 Mbps开始持续增长,一直提升至网络整体吞吐量不再发生变化,得到的结果如图7所示.
从图7可以看出,随着网络拓扑逐渐复杂,网络节点逐渐增多,4种算法的整体吞吐量都呈现增长趋势.

Fig.7 Network throughput experiment图7 网络吞吐实验
另一方面,从整体上来看,FSR算法在相同网络拓扑结构下,相比对照组算法,能够达到更大的网络吞吐量.其中,拓扑1网络环境下,4种算法差距最小,RDL和LRD算法几乎相同,OSPF略好于前两者,LRD算法最终达到约305 Mbps,RDL算法最终达到约320 Mbps,略微优于LRD算法,OSPF算法达到约345 Mbps.FSR算法最终可以达到385 Mbps,相比对照组算法,分别提升约20%,26%和12%.拓扑3中,FSR算法取得了最大的吞吐量优势.对照组算法中,OSPF算法达到约580 Mbps,LRD算法最终取得约640 Mbps的最大吞吐量,RDL算法则可达到720 Mbps.与此相对比的是,FSR算法可以达到最大865 Mbps的最大吞吐量,相比对照组算法,分别提升约49%,20%和35%.
3.3.3 平均路径长度
为了在网络资源受限或者流量分布不均的情况下,充分利用网络资源提高全网吞吐能力,路由路径的调整则必然会存在“舍近求远”的情况,从而达到网络负载的均衡.
然而,一个恰当的平均路径长度也是一个优秀的路由选择算法需要考量的因素.
在4种网络拓扑中,分别运行OSPF,FSR,LRD和RDL这4种算法,同时,利用实验设计阶段选取的网络流量,并分别记录每个算法20次的网络路由调整结果,计算全网源—目的对间的平均路径长度,得到如图8所示的实验结果.

Fig.8 Average path length experiment图8 平均路径长度实验
从实验结果可以看出,随着网络结构更加复杂、网络规模不断增大,除OSPF算法路径不变外,其他各算法的平均路径长度都呈现增长趋势,但除去路径不变的OSPF算法,FSR在4种拓扑情况下平均路径均为最短.其中,拓扑1环境下,3种智能路由算法的平均路径长度差异最小,RDL算法在经过20次更新周期后,平均转发路径长度为8.09,LRD算法为7.29,而FSR算法的平均路径长度为5.89.在拓扑3和拓扑4中,FSR的平均路径长度均大幅度低于对照算法组中的智能路由算法.以拓扑4为例,RDL为28.34,LRD为25.94,同情况下FSR则为16.11,平均路径长度分别降低了43%和38%,但相比OSPF算法依然提升了约79%.
综上所述,通过对4种拓扑下3个算法的测量可以发现,FSR给出的路由选择,其平均路径长度相比对照算法组,有明显的降低,可以以更高的效率完成数据的转发操作.
3.3.4 算法运行时间
除了网络性能之外,一个路由选择算法还需要考虑算法自身的效率问题,效率低下的算法可能导致路由计算开销较大,从而影响算法可用性,为了考察FSR算法的算法效率,我们设计了一组实验,在同样进行20次路由选择的条件下,记录3种智能路由选择算法的运行时间,并在4种不同的拓扑上分别进行该实验.
通过实验可以发现,在4种不同的拓扑下,算法运行时间略有差异,在3种算法的横向对比中,FSR算法的总体运行时间最长.这主要是由于FSR算法与对比组算法相比,为了减少网络中的路由抖动而多了一个处理环节.这一设计一方面确实增强了网络整体运行效率,而另一方面也带来了一定的额外时间成本.
具体来说,FSR算法在20次路由调整过程中,最短用时3.35s,最长用时4.38s,平均用时3.73s.而与之对比的是,对照组算法中,RDL算法最短用时2.28 s,最长用时3.3 s,平均用时2.69 s,LRD算法最短用时2.83 s,最长用时3.68 s,平均用时为3.17 s.FSR算法运行时间确实长于对照组的2种算法,平均运行时间方面,FSR相比RDL要多消耗1.04 s,而相比LRD算法要多消耗0.56 s.
通过上述实验可以看出,FSR算法由于额外的抖动抑制操作,在运行时间上比对照组算法多出了额外的时间开销.但考虑到FSR算法在实际吞吐率测试中带来约30%的带宽提升,不难发现即便存在算法运行速度上的劣势,但FSR算法由于抑制了网络振动,仍旧可以实现比现有机制更好的网络传输效率.
4 相关工作
流量工程和路由策略是互联网技术的基础并受到了学术界和工业界的共同研究.这些研究广泛涉及了互联网的各种应用形式,包括传统网络[7]、数据中心网络[8]和核心骨干网[9].相关研究的核心目标均是为了满足在复杂多变的应用环境中尽可能地优化满足灵活的服务质量要求,而这一个问题的求解则建立在数学模型的建立和求解基础上.然而,正如引言所述,网络规模的庞大和流量需求的多变为这一类问题的数学建模工作提出了巨大的挑战,通常的做法是针对具体应用场景进行必要的简化假设,并以此使得数学模型可以有效求解.然而现实网络环境往往是多种应用需求、流量特性和网络结构的复杂叠加,简化假设在实际场景中往往难以满足.针对上述问题,目前还难以找到一个有效的通用模型,并在优化效果上达到实际使用的需求,因此,传统基于数学模型的网络管理机制越来越难以满足快速发展的网络应用的需求.
另一方面,随着计算能力的提高和数据的爆炸式增长,人工智能得到了极大的发展,强大的计算能力可以模仿更深的神经网络(DNN),而大数据可以提供足够的训练样本.其中人工神经网络和深度学习技术取得了最大的发展,其通过构建更多层次的深度神经网络,实现学习和识别抽象模式,并已广泛应用于图像分类、物体识别、通信以及其他各个相关领域[10-11].
机器学习技术已被广泛应用于解决各类网络管理问题,包括拥塞控制[12-13]、资源分配[14]和视频流的比特率选择[15]等.其中,对于路由选择问题,早期Q路由[16]首次将Q学习[17]应用于网络路由上下文.与传统基于最短路径的路由策略相比,Q路由通过历史规律的学习,可以更加有效地避免网络拥塞并降低传输时延.在Q路由中,每个路由器分别学习从数据包头到输出端口的映射.这涉及路由器以每个数据包分辨率不断交换有关其针对不同目的地的延迟信息.我们认为,在每个数据包级别上以分散方式进行操作,在可伸缩性和通信开销方面提出了重大挑战.
针对这些问题,近年来也取得了一定的研究成果[18-19].其中,LRD算法通过强化学习的方式来进行智能的路由选择,将经典的最小化最大链路利用率作为研究的目标,希望通过历史网络流量来驱动路由的选择.RDL采用了深度卷积神经网络(CNN)来控制网络流量,利用当前请求发送的流量数据来合理地规划路由的路径选择,通过利用在线的方式不断地迭代CNN神经网络,以此来得到更具适应力、平均时延和丢包率更低的模型.然而,正如本文引言讨论的,当前智能路由算法对路由更新时的振动抑制还存在较大优化空间.
5 总 结
随着网络流量的快速增长以及网络应用模式的不断更新,路由机制及网络设备的转发能力面临着更为严峻的考验,传统的、相对固化的路由算法已经很难满足当前不断增长和变化的网络需求.
动态灵活的路由调整机制,以及基于历史数据学习网络流量和路由选择规律的能力,是智能路由算法核心优势所在.本文聚焦于当前智能路由算法在每个路由更新周期所带来的大范围的路由抖动以及由此引发的网络转发效率降低的问题,提出了一种路由抖动敏感的智能路由选择算法,核心思想是在追求全网链路负载均匀分配、充分利用全网转发资源的同时,寻求与当前路由选择变动最小的更新方案,使得每个更新周期带来的路由抖动尽快收敛,提升网络整体转发效率.FSR算法利用CNN生成当前网络拓扑环境的路由方案可行解,并从可行解中寻找路由抖动最小的最优解.实验表明:FSR算法与对照算法相比提升约30%的网络吞吐量,同时显著降低网络丢包和拥塞概率.
未来,我们将会结合具体的网络应用场景,进一步研究更有针对性的其他路由抖动收敛机制,同时重点研究算法时间开销的优化方法,提升FSR算法的执行效率.
作者贡献声明:邵天竺,负责实验方案设计与仿真、数据分析,参与方案设计、论文编写;王晓亮(通信作者),负责方案设计、论文编写,参与实验方案设计;陈文龙,参与方案设计;唐晓岚,参与实验方案设计;徐敏,参与方案设计、数据分析.

