基于三参数Weibull分布的安徽省年最大风速均一性检验

温华洋 朱华亮 刘壮 孔芹芹 马文周 陈凤娇

(1.安徽省气象信息中心，安徽 合肥230031；2.合肥工业大学，安徽 合肥230023)

引言

均一的长序列气象资料是气候变化研究的基础[1－2]，但由于台站在长期观测过程中，不可避免的存在观测方式、观测仪器和周边探测环境改变以及台站迁移等非气候因素造成了长序列数据的不连续[3]。为建立真实的气候序列，众多学者对资料序列的均一性检验和订正工作开展了大量研究，形成了诸多方法。如标准正态均一化检验方法[4](简记SNHT，下同)、二相回归方法[5](TPR)、惩罚最大F检验方法[6](PMFT)等，这些方法在地面资料[7－9]、辐射资料[10]和高空资料[11]均一性检验上取得了一定的进展，形成了系列均一化数据集[12－14]，在气候变化研究等领域发挥重要作用。各种方法的比较表明，根据不同要素、不同区域、不同时间尺度选取不同的均一性检验与订正方法较为有效[15－18]。

风的研究与大气环境治理[19]、风能开发利用[20]和气候变化[21－24]等工作密切相关，但风资料的均一性研究，国内目前仍处于一些尝试性的水平。刘小宁[21]采用SNHT方法对中国主要气象台站年平均风速进行了检验，何冬燕等[22]以两站为例对比分析了直接检验方法(t－检验)和3种间接检验方法(SNHT、PMFT和PMTT(惩罚最大T检验))对年平均风速的检验效果。周昊楠等[23]利用PMFT对新疆地区105个站点年平均风速进行了检验，并分析了造成非均一性的主要原因。彭嘉栋等[24]利用改进的二相回归法对中国中部典型高山站南岳和庐山平均风速进行了检验和订正。这些检验方法中不少方法要求气候序列服从正态分布，然而，有研究表明风速的概率分布并非完全是正态的，如刘小宁[21]使用的690个气象站风速资料序列中，服从正态分布的仅171个，占比不足25%。Stewart和Essenwanger[25]通过45个站点的风速资料研究发现，相较于其他分布，Weibull分布能较好地拟合实测风速的概率分布。Seguro和Lambert[26]研究表明，三参数Weibull分布对于年最大风速具有较高的拟合精度和较强的适应性，并用极大似然法估计出三参数Weibull风速分布的参数。Jandhyala等[27]采用似然比法探究了Weibull模型中的变点检验问题，并对极端气温数据开展应用。这些理论研究为开展基于Weibull分布的风速均一化检验提供了基础。

为此，本文采用基于三参数Weibull分布的变点检验方法，对安徽省1980—2018年元数据记录较为典型的郎溪站(包含了探测环境变化、台站迁移、仪器换型及高度调整等人为因素可能导致变点的情况)年最大风速序列进行检验，依据台站的元数据对检验出来的非均一点产生的原因进行了分析，最后应用该方法对安徽省部分台站1981—2018年年最大风速序列进行检验，并与国内普遍使用的PMFT法、SNHT法进行对比，为风速均一性检验提供参考。

1 资料与方法

1.1 资料与处理

选用安徽省1980—2018年年最大风速资料相对完整的56个国家级气象站作为研究对象，站点分布见图1，其中安徽省北部地区站点分布较为稀疏，南部地区站点分布较为密集。各站观测资料均通过台站—省级—国家级的三级质量控制。为减少气候因素对序列均一性检验结果的影响，需对检验序列进行去趋势处理。首先，针对待检验序列X＝{x1980，x1981，…，x2018}的站点选取参考站，参考站选取标准为:(1)与待检验站点的直线距离小于200 km，地理环境相似；(2)1980—2018年年最大风速资料序列较为完整；(3)与待检验站点的历年最大风速相关系数通过置信度α＝0.05的显著性检验，且排名前3位。其次，对三个参考站的年最大风速序列取平均值形成参考序列W＝{w1980，w1981，…，w2018}。最后，利用待检验台站的年最大风速与参考站进行比值X/W，形成检验序列Z＝{z1，z2，…，z39}，其中i＝1，2，…，39。

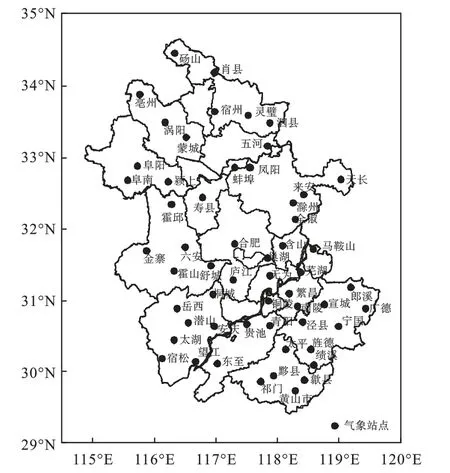
图1 安徽省56个国家气象站站点分布Fig.1 Distribution of 56 national meteorological stations in Anhui province

1.2 研究方法

Weibull分布是可靠性研究领域中应用最广泛的一种统计分布模型，而三参数Weibull分布是Weibull模型中对数据适应能力最强、拟合效果最好的，尤其对风而言[26]。三参数Weibull分布函数见式(1)所示:

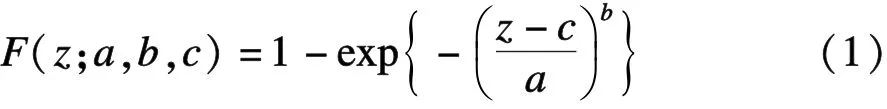
式(1)中，a＞0为尺度参数，b＞0为形状参数，0＜c＜z为位置参数。给出一组序列长度为n的年最大风速序列Z＝{z1，z2，…，zn}，利用K-S方法[28]检验序列是否服从Weibull分布(采用显著性水平为0.05的检验)。对于服从Weibull分布的序列，再利用极大似然估计法[26]得到年最大风速序列的三参数Weibull分布的参数a，b，c，即得到序列Z的三参数Weibull分布函数F(z；a，b，c)。

假设存在一个分割集κ＝{3，4，…，n－2}将年最大风速序列Z分割为两个新的子序列，即Z1＝{z1，z2，…，zk}，Z2＝{zk＋1，zk＋2，…，zn}，其中k∈κ。若序列Z1，Z2均通过K-S检验，则利用极大似然估计法可以得到序列Z1，Z2的三参数Weibull分布函数F1(z；a1，b1，c1)和F2(z；a2，b2，c2)。如果序列Z在分割点k发生突变，则有F1(z；a1，b1，c1)≠F2(z；a2，b2，c2)。为此，可以定义检验统计量:

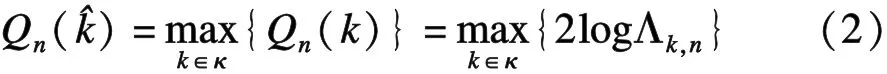
式(2)中，Λk，n的定义见文献[27]，∈κ。当QN(＾k)大于样本量对应的检验统计量阈值(表1)时，认为序列Z在＾k处发生突变；反之，则未发生突变。对于发生突变的序列，在突变点＾k处应用二分法将序列分为两个子样本，并分别进行均一性检验，继而检测出序列的全部非均一点，而当子样本长度小于8时，则不再进行均一性检验。

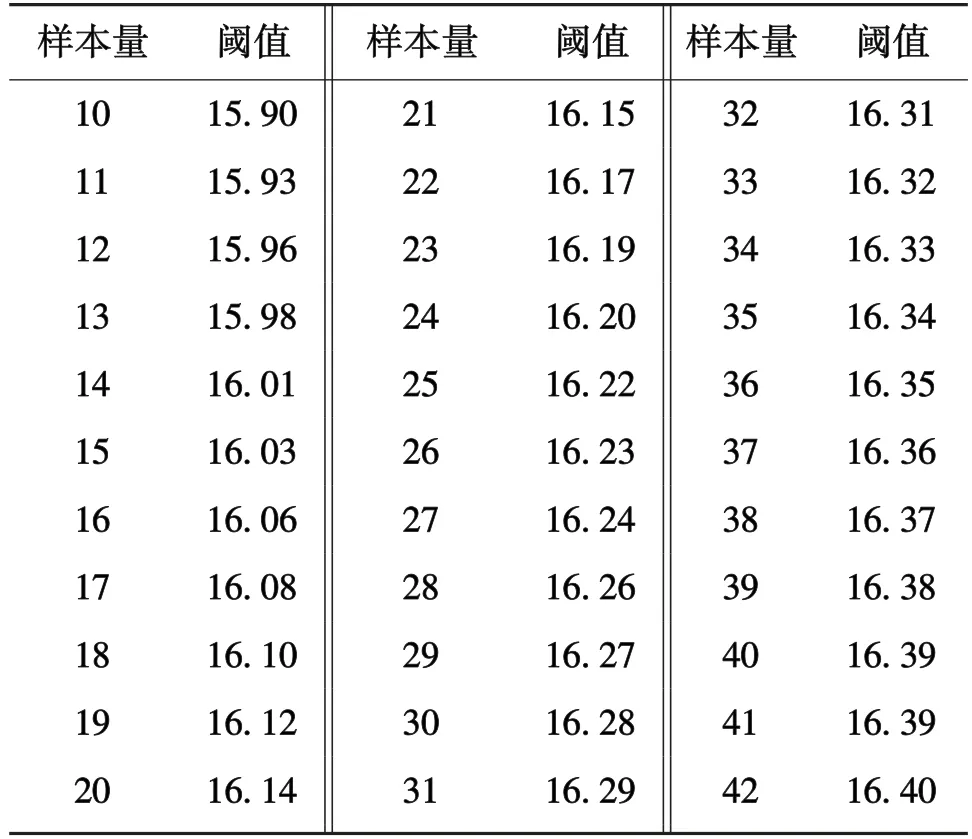
表1 不同样本量对应的显著性水平为0.05的检验阈值Table 1 Test threshold of significance level at 0.05 in terms of different sample sizes

2 结果分析

2.1 以郎溪站为例的年最大风速的均一性检验

2.1.1 序列去趋势

1980—2018年郎溪气象站年最大风速原始序列和去趋势序列见图2。由图2可知，年最大风速序列的波动较大，序列的最大值达到16.1 m·s－1，最小值达到6.3 m·s－1，其中1980—1998年的年最大风速为10.3—15.3 m·s－1，均 值 为13.1 m·s－1，并 以1.16 m·s－1/10 a的速度下降。从1999年开始，年最大风速明显变小，1999—2010年的年最大风速为6.3—11.0 m·s－1，均值为8.3 m·s－1，并以1.73 m·s－1/10 a的速度下降。到2010年之后，年最大风速又开始明显变大，2011—2018年的年最大风速为9.8—16.1 m·s－1，均值为13.5 m·s－1，并以2.07 m·s－1/10 a的速度下降。总体上，整个序列呈现下降趋势。为减少气候因素对序列趋势的影响，选用参考站进行去趋势处理。经检查发现，马鞍山站、泾县站和繁昌站的年最大风速资料序列较为完整，与郎溪站的距离较近，地理环境相似，年最大风速相关系数分别为0.77、0.33和0.33，且通过显著性水平α＝0.05的显著性检验。利用马鞍山站、泾县站和繁昌站的年最大风速序列对郎溪站观测序列进行去趋势处理，得到郎溪站年最大风速去趋势序列(图2b)。由图2b可知，序列在1999年、2010年前后发生了显著的变化，将整个序列分为1980—1998年、1999—2010年和2011—2018年三段，各段内序列基本无变化趋势。

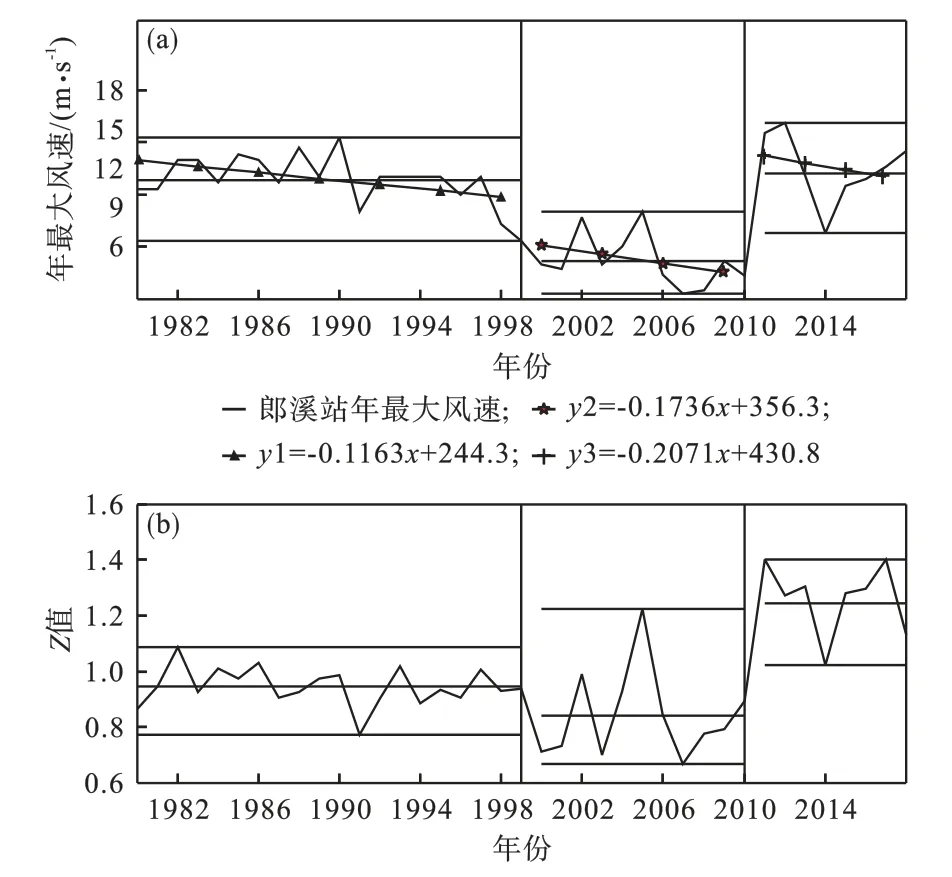
图2 1980—2018年郎溪气象站年最大风速原始序列(a)和去趋势序列(b)Fig.2 The original sequence(a)and detrended sequence(b)of annual maximum wind speed at Langxi meteorological station from 1980 to 2018

2.1.2 Weibull分布检验及参数估计

针对郎溪站1980—2018年的年最大风速去趋势序列Z，依次取分割点k＝3，4，…，n－2(对应年份为1982，1983，…，2016)，将序列分割为左右两个子序列，利用K-S方法分别检验分割点左侧序列和右侧序列是否服从Weibull分布。图3a为各分割点左侧序列和右侧序列K-S检验的P值，可以发现各分割点两侧序列的检验P值均大于0.05，通过显著性检验，表明各分割点两侧的序列均服从Weibull分布。为此，可以采用极大似然估计法得到各分割点两侧序列的三参数Weibull分布的参数a，b，c，即得到各分割点两侧序列的三参数Weibull分布函数F(z；a，b，c)。如果序列Z在某一分割点处存在非均一点，则Weibull分布的参数a、b或c一定发生变化，通过线性变化＾Z＝(Z－c)/a，将Weibull分布的位置参数c标准化为0，尺度参数a标准化为1，则可以侧重于研究Weibull分布形状参数b的变化。图3b为各分割点两侧序列的Weibull分布的形状参数估计值，可以看出形状参数在2010年附近出现了较大的跳跃，表明2010年前后可能出现了非均一点。

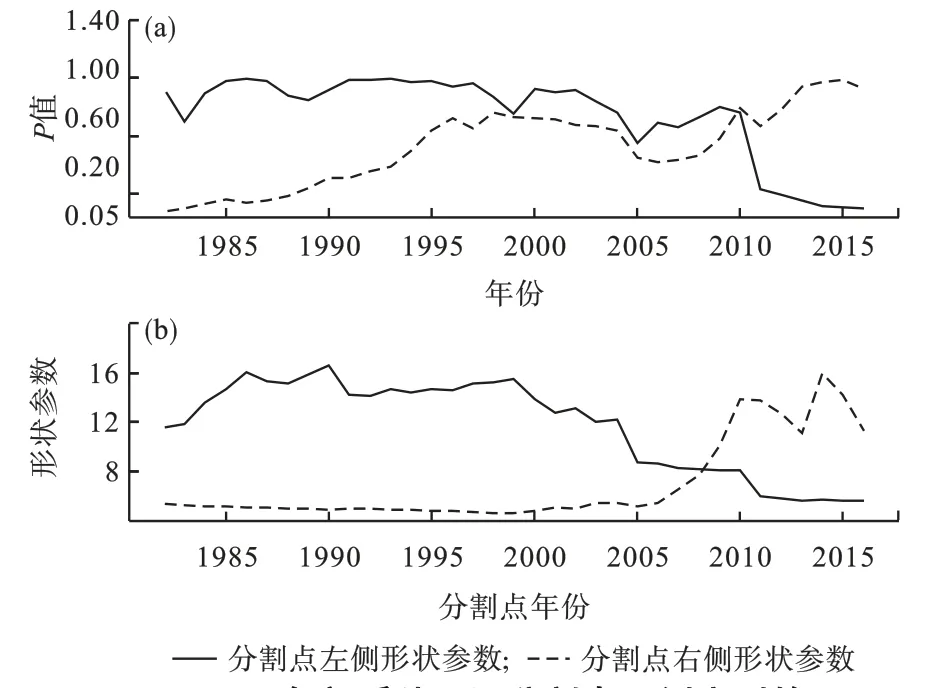
图3 1980—2018年郎溪站不同分割点两侧序列的Weibull分布K-S检验P值(a)和形状参数估计值(b)Fig.3 The P-values(a)and shape parameter estimation values(b)of Weibull distribution′s K-Stest on two side sequences at different segmentation points at Langxi meteorological station from 1980 to 2018

2.1.3 年最大风速的均一性检验

利用式(2)可以得到郎溪站1980—2018年的年最大风速去趋势序列Z在不同分割点的检验统计值Qn(k)，如图4a所示，可以看出序列的检验统计值在2010年达到最大，且大于样本量对应的检验统计量阈值16.38，表明郎溪站的年最大风速序列在2010年发生了突变。利用二分法将序列分为1980—2009年和2011—2018年两段，并分别进行均一性检验，发现1980—2009年的序列检验统计值在1999年达到最大(图4b)，且大于样本量对应的检验统计量阈值16.14，表明郎溪站的年最大风速序列在1999年也发生了突变。再对子样本1980—1998年和2000—2009年进行均一性检验时，未发现非均一点。经查郎溪站历史沿革和《气象台站观测环境综合调查评估报告(安徽省郎溪)》，2007年郎溪站地面探测环境评分仅58.6分，不符合要求的人为障碍物累计遮挡方位达到357.2°，人为障碍物主要是1998—2000年建设完成的住宅楼、宿舍楼、办公楼和厂房。随着建筑物数量增多和高度增加，会对空气的流动产生阻挡作用，造成观测场的测量风速明显变小。2011年观测场由建筑物密集的城区搬迁至正北方向约3 km探测环境较好的郊区，其地面探测环境评分为96.1分，无人为障碍物，因而探测到的风速变大，故认为该方法检验出的1999年和2010年两个非均一点是真实存在的，考虑1999年和2010年前后观测方式和统计方法无变化，风速传感器未换型，且仪器高度无变化，认为探测环境变化和站址迁移是郎溪站年最大风速序列产生非均一点的主要原因。

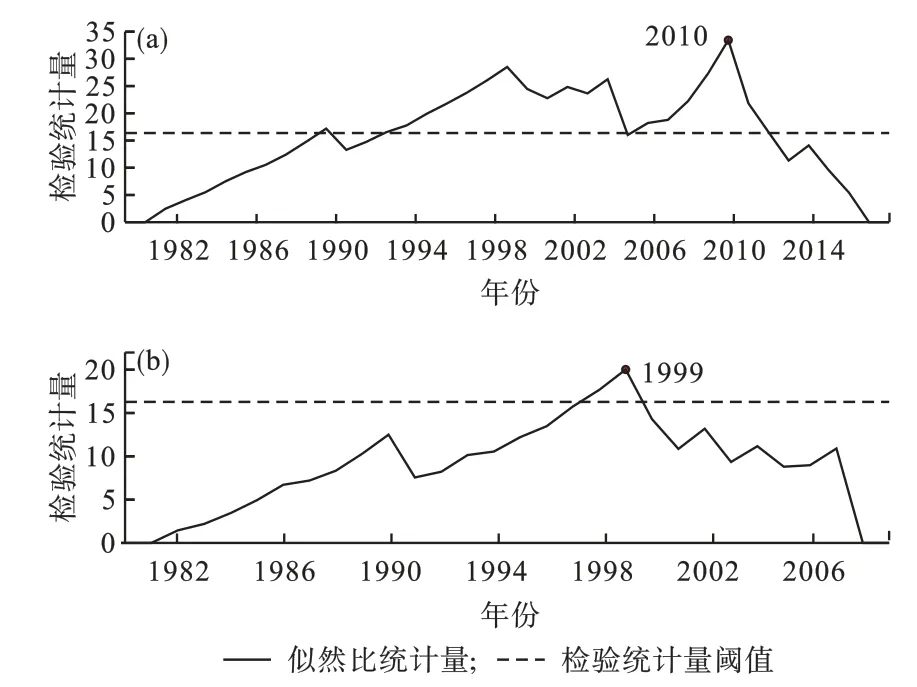
图4 1980—2018年(a)和1980—2009年(b)郎溪站年最大风速序列不同分割点的检验统计量Fig.4 Test statistics of annual maximum wind speed sequence at different segmentation points during 1980-2018(a)and 1980-2009(b)at Langxi meteorological station

2.2 Weibull检验与PMFT、SNHT检验效果对比

采用三参数Weibull检验对安徽省1980—2018年年最大风速资料相对完整的56个台站进行均一性检验，同时也用PMFT和SNHT方法对这些台站进行均一性检验，其中SNHT方法选取参考站标准与Weibull方法一致，检验结果如表2和表3。

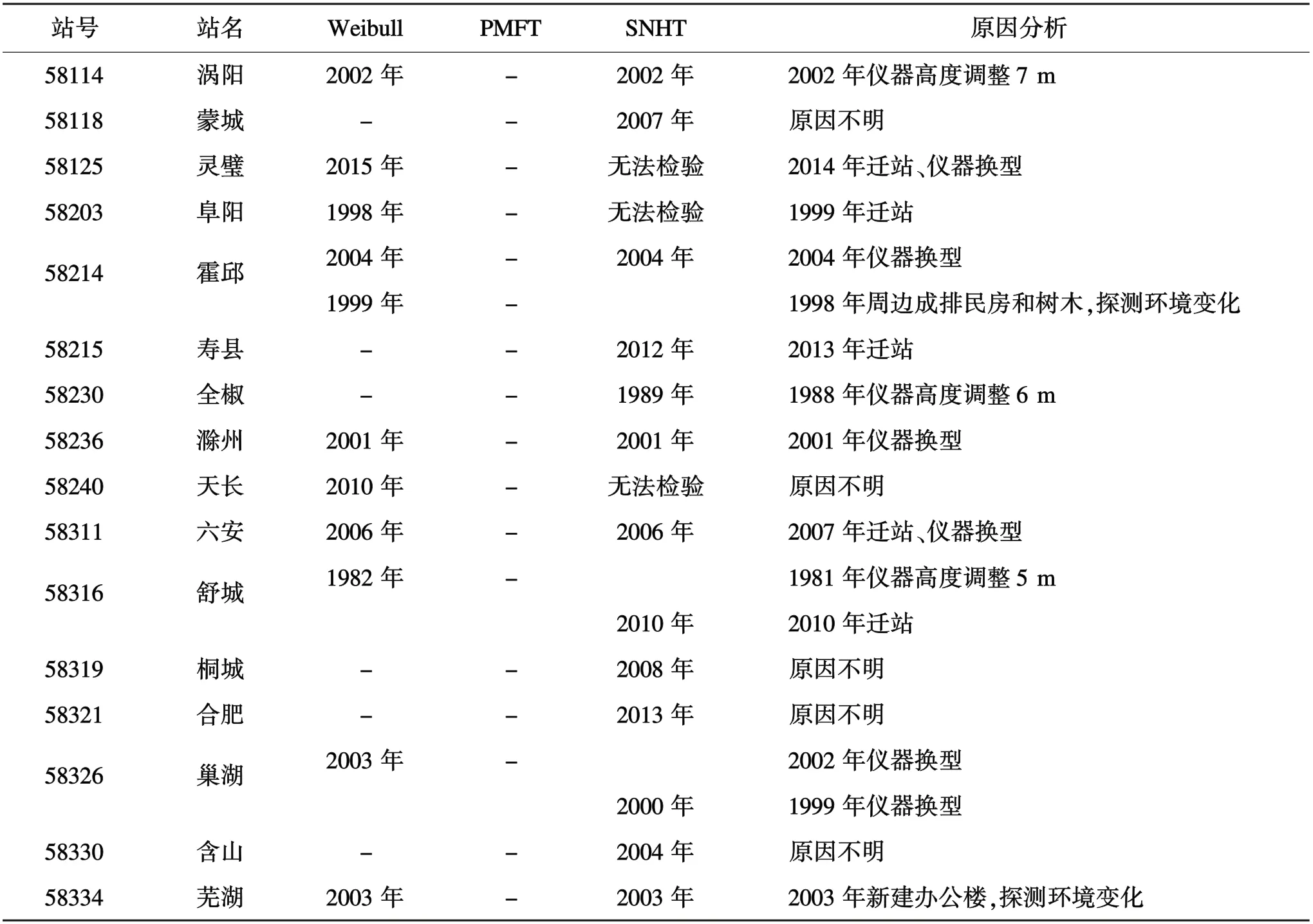
表2 1980—2018年安徽省56个台站最大风速资料Weibull、PMFT和SNHT检验结果及原因分析Table 2 Test results of maximum wind speed data using the Weibull，PMFT，and SNHT methods and cause analysis at 56 stations of Anhui province from 1980 to 2018

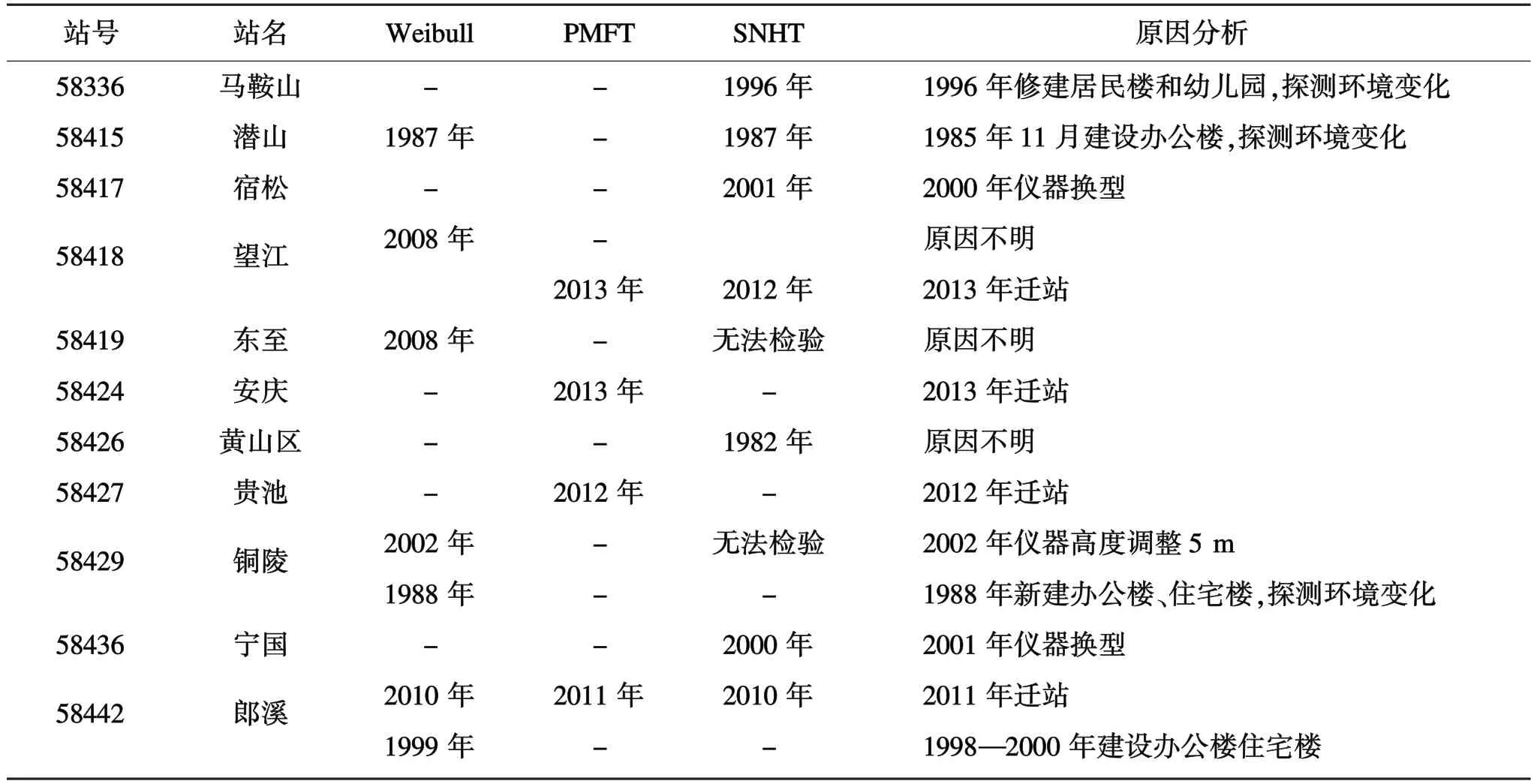
注:“－”为没有突变年份；“无法检验”为该台站的年最大风速序列(或取对数后)不服从正态分布，无法用SNHT法检验；存在多个非均一点的，按检验结果前后次序给出。

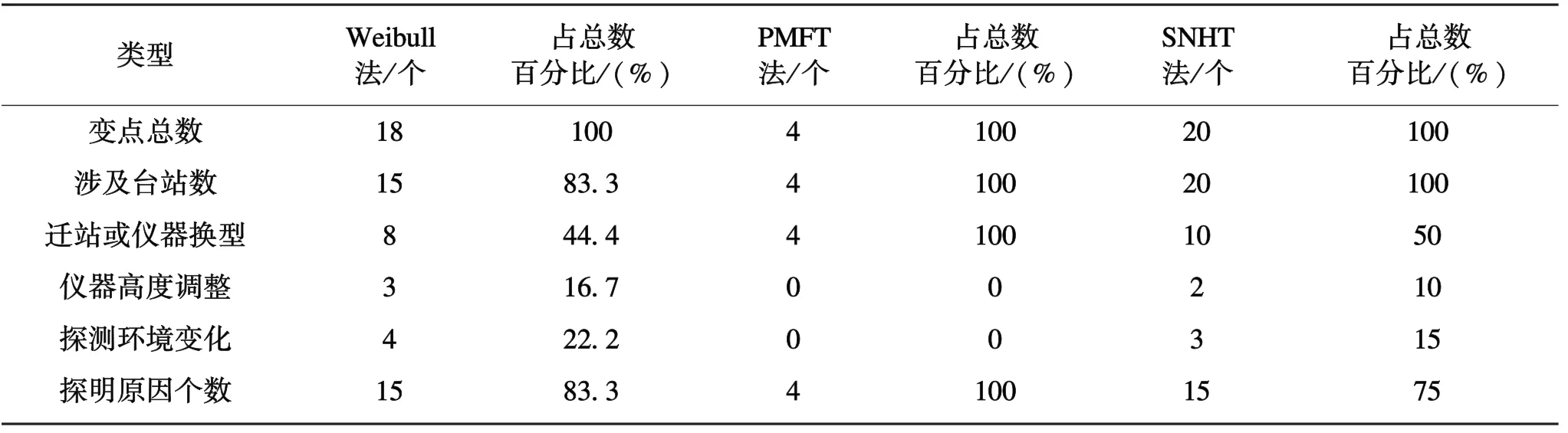
表3 1980—2018年安徽省56个台站最大风速资料Weibull、PMFT和SNHT检验结果统计Table 3 The statistical results of the test maximum wind speed data using the Weibull，PMFT and SNHT methods at 56 stations of Anhui province from 1980 to 2018

在Weibull检验方面，56个台站的年最大风速序列均通过K－S检验，表明序列均服从Weibull分布，采用Weibull分布检验发现56个台站中有15个台站存在非均一点，合计检测出18个非均一点，其中霍邱站、铜陵站和郎溪站均检测到2个非均一点。18个非均一点中有15个探明原因，占比为83.3%，其中因迁站和仪器换型造成非均一点的有8个，占比为44.4%，因仪器高度调整或周围障碍物导致探测环境变化的有7个，占比为38.9%，另外3个非均一点没有得到相应台站历史沿革和探测环境综合调查的印证，存在误判的可能性；在SNHT检验方面，56个台站中有19个台站未通过正态分布检验，对这些台站的年最大风速序列取对数变换后，仍有6个台站未通过正态分布检验，对剩下的50个台站进行SNHT检验，在检测出符合显著性的非均一点之后，再对分割点前后的两个序列做检测，检查两个序列是否均服从正态分布，发现有5个台站分割点前后的分布不同时服从正态分布。故实际上有11个台站是无法用SNHT法检验的。在剩下的45个台站中，使用SNHT方法找到了20个非均一点，其中因迁站和仪器换型造成非均一点的有10个，占比为50%，因仪器高度调整或周围障碍物导致探测环境变化的有5个，占比为25%，没有得到相应台站历史沿革和探测环境综合调查印证的有5个，占比为25%；同样，在PMFT检验方面，50个年最大风速序列通过正态分布检验的台站中检测出4个台站各存在一个非均一点，查阅台站历史沿革发现4个非均一点均由迁站造成。

综合比较Weibull、PMFT和SNHT检验结果发现，1980—2018年安徽省56个台站的年最大风速序列均通过Weibull分布检验，而有11个台站的年最大风速序列未通过正态分布检验，表明年最大风速序列更符合Weibull分布。56个台站的年最大风速序列均可用Weibull检验，而只有50个台站的序列可以采用PMFT检验，45个台站的序列可以采用SNHT检验，且PMFT只检测出4个非均一点，对年最大风速序列非均一点的敏感程度不如Weibull和SNHT。SNHT检测出20个非均一点，Weibull检测出18个非均一点，但Weibull方法找到的18个非均一点中有15个能得到台站历史沿革或者综合调查等的印证，检测准确率高达83.3%，而SNHT方法的检测准确率只有75%，相较于SNHT方法，Weibull方法的检测准确率更高。

3 结论与讨论

(1)采用三参数Weibull分布对1980—2018安徽省郎溪站的年最大风速资料序列进行均一性检验表明，郎溪站年最大风速资料序列在1999年和2010年存在非均一点，查阅郎溪站台站历史沿革发现，探测环境变化和站址迁移是郎溪站年最大风速序列产生非均一点的主要原因。

(2)通过对1980—2018年安徽省56个台站的年最大风速资料序列的均一性检验发现，56个台站的年最大风速序列均通过Weibull分布检验，而只有50个台站的年最大风速序列通过正态分布检验，表明年最大风速序列更符合Weibull分布。在检验结果方面，Weibull法检测出18个非均一点，其中有15个点对应着台站迁移、仪器换型、仪器高度调整和探测环境变化等原因，检验准确率为83.3%；PMFT法检测出4个非均一点，这4个点均由迁站造成，检验准确率为100%；SNHT检测出20个非均一点，其中有15个非均一点得到台站历史沿革的印证，检验准确率为75%。

(3)综合比较Weibull、PMFT和SNHT检验结果发现，PMFT法只检测出4个非均一点，对年最大风速序列非均一点的敏感程度不如Weibull和SNHT，SNHT法对待检序列要求较高，56个站点中有11个站点无法使用，且检验准确率不及Weibull法，这表明Weibull方法在年最大风速序列的均一性检验中更具有优势，但从检验过程来看，仍存在PMFT法和SNHT法同时检测出而Weibull未检测出的非均一点，如望江站2013年迁站引起的非均一点，表明Weibull分布检验存在着漏检的情况，因此可以考虑将三者结合同时检验，相互补充，相互参照，以提高检测的准确率。

(4)本研究重点探讨了基于三参数Weibull分布的变点检验方法对年最大风速序列均一性检验效果，但对年平均风速序列均一性检验效果如何尚未讨论，可作为后续研究工作，并与文献[21—23]研究结论进行对比分析，进一步探讨该方法的优劣。此外，很多断点是由台站迁移、仪器变更等原因造成的，这些原因不仅会导致年最大风速序列出现断点，也可能会导致相应的年平均风速序列出现断点，两者检验结果的互相比较、印证，也可作为后续工作重点进行探索。