高重力坝坝基岩体变形模量回复研究
廖 彬, 聂德新
(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059; 2.四川省投资集团有限责任公司,成都 610059)
大型水电站所在高山峡谷区,岩体坚硬、地应力量值高、卸荷明显、风化深度大,而高混凝土坝大多以微新、弱风化下带的Ⅲ1-Ⅱ级坚硬岩体作为坝基[1-2],必须对强风化-弱风化上带和卸荷岩体进行较大规模的爆破开挖才能达到要求,由此而造成坝基岩体的松弛、变形模量的降低,对大坝的变形稳定性带来大的影响,是高坝坝基岩体研究的重点。
对岩体变形模量的研究,无论以现场岩体变形试验成果进行评价,还是从岩体的其他特征指标进行评价都有较为成熟的技术或方法。D.U.Deere等[3]用钻孔岩心的RQD指标评价岩体变形模量;Z.T.Bieniawski[4-5]研究了岩体的RMR分级,提出了用分级指标选取变形模量;E.Hoek等[6]研究了不同岩体类型的变形模量和强度参数;中国水利水电勘察国标规范中给出了不同岩级的变形模量[1]。研究弹性波速结合一定的现场试验变形模量,建立起动静参数的关系去获得岩体变形参数有广泛的研究[7-10]。近20年来,溪洛渡、小湾、拉西瓦、白鹤滩、黄登等世界级大型水电站超高混凝土坝的兴建,对岩体变形模量和强度参数以大量的、系统的建前、坝基开挖资料,从坝址岩体的风化分带、卸荷程度、开挖爆破松弛带、岩体质量分级,对岩体的变形模量和强度参数作了新的、有开创性的研究,综合评价水平有了大的进展[11-16]。
由于岩体模量是应力、应变的函数,在河流初始下切边坡尚未形成时,处于深埋状态下的岩体的原位模量基本上为新鲜岩体的模量;伴随河谷高大边坡的逐渐形成,岩体应力释放,外部风化营力的进入,边坡岩体卸荷带、风化带的逐渐形成,岩体变形模量和强度参数的下降基本上是同步的,因此应力状态的变化是其主要因素之一。对地应力场特征、地应力的测量、地应力场反演已进行了较多的研究[17-25],符文熹[26]较为深入地研究了地应力对岩体变形模量的影响及变形模量取值,是值得探索的方向。本文以官地水电站为研究载体,用岩体应力状态的变化研究高重力坝大规模开挖减载、岩体松弛回弹、变形模量的降低和大坝建成后高重力坝压重后坝基岩体变形模量的回复。
1 工程概况及地质简况
官地水电站位于雅砻江下游,混凝土重力坝顶部海拔高度 1 334 m,最大坝高171 m。
官地坝址河谷深切、高度大、两岸地形坡度陡、河谷呈“V”形,河水面海拔高度 1 205 m左右,两岸山顶海拔高度 2 880 m(图1、图2)。坝址区所在大地构造部位为康滇地轴与丽江台缘拗褶带的交界部位,地层为二叠系峨眉山玄武岩,似层面产状260°∠80°,大坝所在部位无大的断层,两岸岩体弱风化深度11~80 m,弱卸荷深度9~88 m。

图1 官地河谷地形Fig.1 The topography of Guandi River Valley

图2 官地电站修建中河谷地形Fig.2 The river valley topography of the Guandi power station under construction
坝址位置测试的最大主应力方位为NW向,与其所在大的“川滇菱形断块”的构造应力场最大主应力方向基本吻合。通过对区域和坝址地应力场的数值分析,用新建立的弹性力学三个方向余弦计算公式,经过计算、检验,坝址初始构造最大主应力方向及量值:σ1=7.75 MPa,方向NW310°∠10°;σ2=5.25 MPa,σ3=2.25 MPa。
2 力学分析的基础及研究方式
2.1 力学方程
分析岩体模量的变化的力学基础,是有关平均应力与体积模量的关系

(1)

对于平均应力可以由三向主应力的和获得
(2)

对于体积模量,可以弹性力学的相关公式计算
(3)
式中:K为体积模量;E为岩体模量(弹性模量或变形模量);μ为泊松比。
在当前的岩体力学研究中,大多以变形模量作为变形的主要参数,现场岩体变形试验就以弹性力学的“布氏”方程作为计算变形模量的基本公式
E=π(1-μ2)pD/4W
(4)
式中:E为变形模量(若以弹性变形值代入,则为弹性模量);μ为泊松比;p为板上压力;D为承压板直径;W为变形值。
在应力、应变计算中,若以变形模量作为参数,则计算获得的为全变形。
体积变化率(体积应变)θ
θ=ΔV/V=Δεx+Δεy+Δεz
(5)
式中:Δεx、Δεy、Δεz分别为x、y、z三个方向的应变。
由式(1)(2)(5)得
(6)
式(6)便是分析岩体应力变化、体积应变改变时模量变化的基本力学方程。
2.2 研究方式
由于斜坡及坝基岩体的应力状态除符合弹性力学的基本规律外,由于地形的不均匀变化、材料的突变(断层等弱面)均会造成应力的变化。为了获得坝基模量变化的规律或总的特征,本文采用以下方式来处理:①将斜坡地形中个别突变的部位作适当的光滑;②将岩体中的小的结构面以岩体质量的综合岩级纳入模型;③材料的物理力学参数,按地质剖面展示的岩级进行选值;④力学分析以有限元计算获得应力、应变资料作为模量变化分析的基本资料;⑤以力学分析方法研究坝基岩体在重力坝重力作用下模量的回复,按坝基开挖前、坝基开挖、重力坝修建至设计的高度时坝基岩体变形模量的三个段次作比较分析;⑥应当充分认识到用力学分析方法研究坝基模量,由于涉及多种简化处理(或多种设定),仅在以力学理论揭示的确存在坝基岩体在重力坝压重后模量有回复的现象,而不完全去刻画岩体涉及的复杂变化。
3 坝基开挖爆破松弛带的确定
坝基的开挖,基本上是爆破开挖方式,两岸坝肩开挖大多以平行开挖面进行预裂爆破。河床部位开挖大多为水平预裂爆破。尽管对坝基开挖的冲击较其他大药量爆破要小一些,但仍有一定厚度的岩体被裂化、质量下降、力学参数降低,成为与混凝土坝接触面间的薄弱地带,成为表层抗滑稳定性需认真注意的部位。
官地坝基开挖中,对爆破松弛带的厚度采用物探声波测试,根据波速的变化来分析、确定厚度。为了获得坝基开挖松弛带的平均厚度、波速,筛选从地表开始有测试资料的测孔,列于表1。从表中资料可以看出:①大部分测孔松弛带波速低,有个别孔波速高,应视为松弛带不明显;②松弛带的厚度大多在1~2.5 m;③以各孔的平均厚度作为坝基爆破松弛带的厚度,以平均波速为爆破松弛带的波速。

表1 坝基爆孔声波测试结果 Table 1 Acoustic test results of blast hole in dam foundation
坝基爆破松弛带厚度为2.10 m;坝基爆破松弛带波速为3.338 km/s。
4 研究模型的建立
4.1 分析模型
分析坝基岩体在重力坝压重下变形模量的回复,涉及河谷的形状、地层岩性、构造、岩体应力状态、岩体物理力学性质、河谷下切的形态和建坝要开挖的形态,以及建坝后地基的应力状态,因此,建立合理、符合实际的数值分析模型是研究重力坝坝基岩体变形模量回复的主要工作。
4.1.1 河谷形态、高度的选取
官地河谷深度大、坡度陡,两岸地形也有变化,从图1和图2可以看出河谷两侧山顶的海拔高度在 2 880 m左右,雅砻江河水的海拔高度在 1 205 m左右,而目前坝址地形图涉及的海拔高度在 1 500 m左右,地形剖面海拔高度也在 1 500 m左右,这对分析整个峡谷岩体的应力状态是不够的,还必须获得整个峡谷区的地貌形态。
为获得官地河谷较可信的地貌形态,以坝址1∶1 000地形图为基础,将其纳入包含有两岸高处地形的库区地形图中,以此大范围地形图为基础,建立三维地形模型(图3)。

图3 坝址大范围三维地形模型Fig.3 3D massive terrain model around the dam site
对建立的三维地形进行剖切,获得Ⅶ线(坝轴线)地形剖面,并与地质上的Ⅶ线剖面进行拟合(图4)。从图上可以看出,地形线基本一致,表明地形模型是可信的。
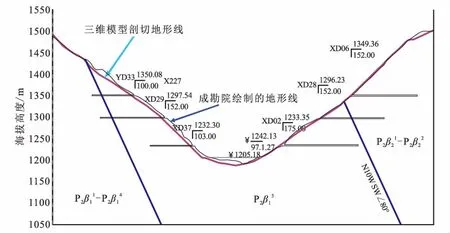
图4 剖切地形模型得到的Ⅶ剖面地形 与地质剖面地形Fig.4 The Ⅶ section topography and the geological section topography obtained by the sectional topography model
剖切至模型高处,获得河谷地形剖面,并对部分突点作适当光滑得到计算模型的地形(图5),从图中可以看出蓝颜色的地形线可以作为计算模型中河谷地形线。

图5 计算剖面Ⅶ线(轴线剖面)概化地质模型Fig.5 Generalized geological model for calculating profile Line Ⅶ (axial profile)
4.1.2 地层岩性模型
坝址二叠系岩性层为:阳新灰岩(P1y);泥质粉砂岩、砂岩、角砾状灰岩(P1p);凝灰岩、角砾状灰岩(P2β11); 含斑玄武岩、凝灰岩(P2β12);致密玄武岩、火山角砾集块岩(P2β13);含斑玄武岩、角砾熔岩(P2β14);辉斑玄武岩、角砾集块熔岩(P2β15);杏仁状玄武岩(P2β21);致密玄武岩、杏仁状玄武岩(P2β22);致密玄武岩(P2β23)。
坝址无大的断层,表2是坝址主要地层及在坝线剖面上岩层界线中心坐标,以此构建圆盘模型,纳入坝址三维地形模型,剖切得到计算剖面地质概化模型(图5)。

表2 坝址主要岩性层产状及中点坐标Table 2 Attitude of major rock formation at dam site and relevant midpoint coordinates
从图5中可以看出与大坝直接相关的地层为P2β15辉斑玄武岩、角砾集块熔岩,与Ⅶ剖面(含高处)相关的岩性层为P2β11-P2β14、P2β15、P2β21、P2β22。
4.2 初始构造应力方位、量值和岩体力学参数
4.2.1 初始模型和基本岩级物理力学参数
以概化的Ⅶ线(轴线剖面)为初始地质结构模型。岩体物理力学参数:河流未下切时各层岩体取初始岩体(新鲜岩体)参数;现今河谷各层岩体按对应岩级取值;爆破松弛带用平均声波纵波速度取Ⅳ级岩体参数;混凝土坝体的参数用多个大型水电站选用值,选取的岩体力学参数见表3。

表3 计算模型岩体及坝体参数Table 3 Calculation of model rock mass and dam parameters
4.2.2 计算的基本模型及开挖、坝体模型
根据地形、岩性、岩体等资料,图6是构建的用于计算的整个河谷基本模型。

图6 整个河谷基本模型Fig.6 Basic model of the entire valley
图7为坝基主要岩级模型,表浅部为Ⅳ级岩体,浅部为Ⅲ1级岩体,下部为Ⅱ级岩体,爆破松弛带为Ⅳ级岩体。
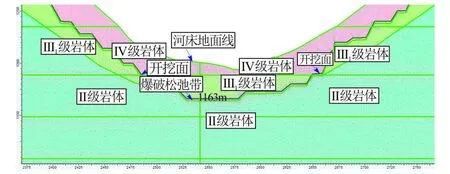
图7 坝基主要岩级Fig.7 Major rock mass levels of dam foundation
图8是建立的坝基开挖模型,开挖线按工程实际设定,河床表面海拔高度 1 200 m,重力坝建基面海拔高度 1 163 m,最大开挖深度37 m,两岸边坡开挖的起始海拔高度为 1 395 m,水平方向挖深35~50 m。
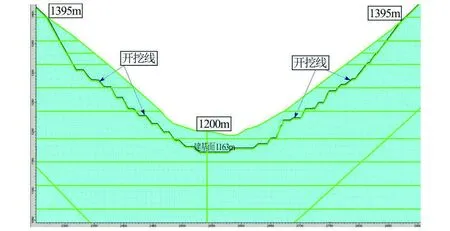
图8 坝基开挖模型Fig.8 Dam foundation excavation model
图9为重力坝模型,顶部海拔高度为1 334 m,河床建基面海拔高度为 1 163 m,爆破松弛带取检测的平均厚度2.1 m。每40 m高差设置水平线,以利于获取同高程单元的信息开展对比;河床布铅直线以利于分析纵向单元信息时纵向坐标相同。

图9 坝体及坝基模型Fig.9 Models of dam body and dam foundation
5 坝基岩体应力状态
5.1 自然河谷应力状态
由前面用应力、体积应变分析岩体模量的公式(1)~(6)可知,岩体应力的变化和体积应变的变化,将引起岩体模量变化。为此,在分析坝基岩体在重力坝重力作用下模量发生回复前,应先了解坝基岩体在各个阶段(自然河谷、坝基开挖、重力坝浇筑后)应力的变化特征。
5.1.1 最大主应力
图10为官地河床部位最大主应力,从图中可以看出:①河床部位,最大主应力量值呈环带状增大→集中增高→减小→逐渐增高现象;②河床表面 1 200 m的海拔高度σ≈0 MPa,向下增大;③河床下部海拔高度 1 148 m部位出现最大主应力集中包,量值46.43 MPa;④拟建的建基面位置(海拔高度 1 163 m)σ1=31.11 MPa,在应力集中包之上; ⑤应力集中包向下应力减小,下延深度172 m(海拔高度 1 069 m),量值36.71 MPa,呈现减小趋势到海拔高度876 m以下(深度124 m)才增加。
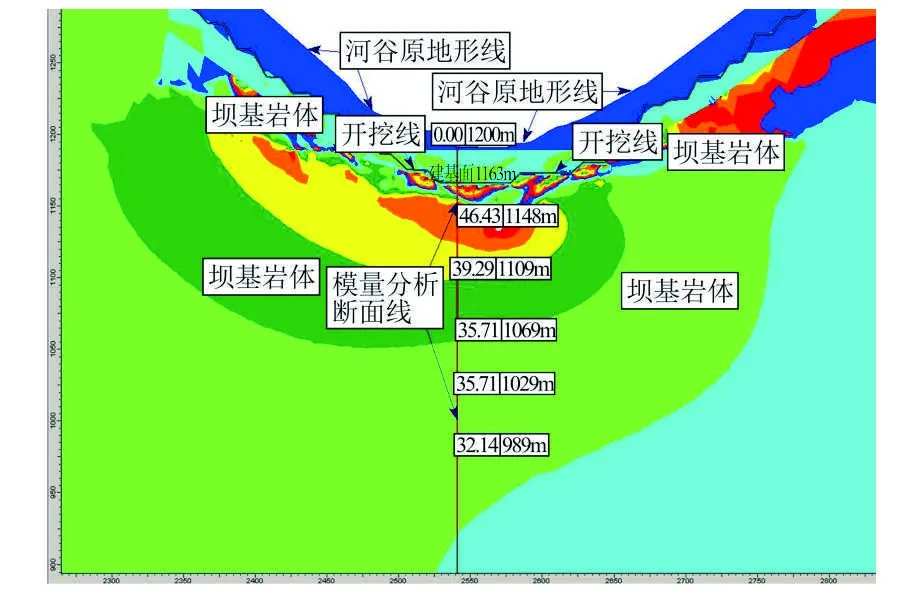
图10 河床部位最大主应力Fig.10 Maximum principal stress of the river bed
5.1.2 最小主应力
图11为河床部位最小主应力,河床表部应力接近0,向下逐渐增大,至92 m深度(海拔高度 1 108 m)为12 MPa。
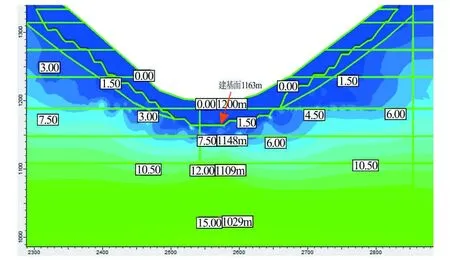
图11 河床部位最小主应力Fig.11 Minimum principal stress of the river bed
5.2 坝基开挖后河床部位岩体应力状态及变化
图12为坝基开挖后,河床部位最大主应力。从图中可以看出:①建基面(海拔高度 1 163 m)以下,最大主应力量值仍呈环带状分布;②在建基面下30~40 m出现应力集中包,量值50 MPa(海拔高度 1 130 m),较天然河床下部应力集中包出现的位置(海拔高度 1 148 m,图10)下延15 m左右;③建基面(海拔高度1 163 m)以下15 m(海拔高度1 148 m)的应力σ1=10.71 MPa,较开挖前的46.43 MPa下降35.72 MPa,表明岩体有较大的松弛。
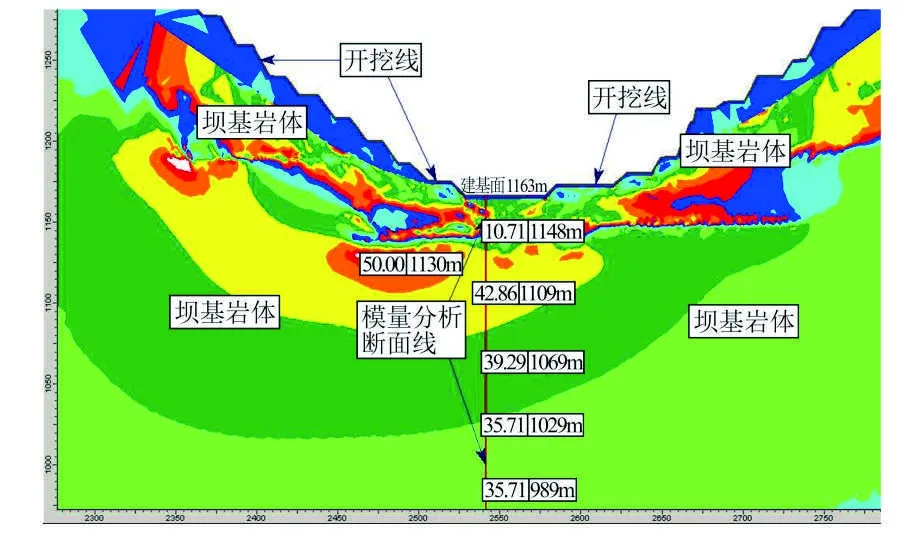
图12 开挖后河床部位最大主应力Fig.12 Maximum principal stress of the river bed after excavation
图13为开挖后河床部位最小主应力,从图中可以看出应力量值的变化与开挖前差异不大。

图13 开挖后河床部位最小主应力Fig.13 Minimum principal stress of the river bed after excavation
图14为计算的坝基开挖后,河床部位岩体回弹变形值,从图中可以看出:①建基面(海拔高度1 163 m)岩体回弹值6.53 cm;②海拔高度1 109 m(建基面下54 m),岩体回弹值3.67cm;③河床岩体回弹的影响深度超过100 m。
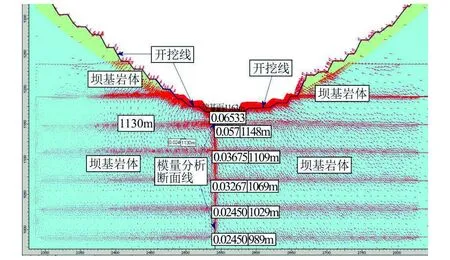
图14 坝基开挖后河床岩体回弹变形Fig.14 Rebound deformation of rock mass of river bed after dam foundation excavation
岩体应力的变化、岩体的回弹,预示河床开挖后岩体模量将降低。
5.3 重力坝浇筑至坝基岩体应力的增加值分析
图15为填筑重力坝(未蓄水)至海拔高度 1 334 m的河床部位最大主应力,从图中可以看出:①建基面(海拔高度 1 163 m)应力为4.0 MPa,与坝的自重相当;②建基面之下海拔高度 1 148 m原应力集中包处,量值30.0 MPa。

图15 重力坝浇筑至1 334 m时河床最大主应力Fig.15 Maximum principal stress of river bed when gravity dam poured to height of 1 334 m
图16为仅考虑坝体自重,河床部位岩体最大主应力的增加值,从图中可以看出:①建基面(海拔高度 1 163 m)增加3.6 MPa;②海拔高度945 m(建基面之下218 m)仍有2.1 MPa;③坝体自重应力呈环带状向下增加,开口大致与谷宽相当。

图16 坝体自重在河床部位的应力值Fig.16 The stress value of the dead weight of the dam at the riverbed
6 以力学方式研究官地水电站重力坝坝基岩体模量的回复
前面分析了河床坝基岩体应力的变化,由于应力状态变化,岩体将随应力的降低松弛回弹——模量降低;随重力坝重力的加载,岩体又将被压密(或压回),变形模量将发生回复。对于模量回复,最完善的方法应该以检测资料、变形监测资料和应力变化资料来开展分析:用预留的钻孔,分别按开挖前、开挖后、灌浆后、重力坝浇筑至坝顶未蓄水前4个主要阶段检测岩体波速的变化,分析岩体模量的变化;以各时期监测到坝基的变形量分析坝基的模量;然后用应力变化分析坝基模量的变化。目前已建的重力坝大多仅有其中的一项资料,且多为变形监测资料,而开挖前、开挖后、灌浆后、大坝浇筑开始至坝顶各时段系统的、可以对位的、连续的声波测试资料,由于施工的干扰很难实现,目前尚未见到系统成果。本文用应力状态分析模量的回复,因涉及官地河谷的应力状态、初始岩体力学参数的精确性、坝基岩体结构、岩体质量等众多问题,限于官地电站河床开挖前、筑坝后测试成果(声波等)基本没有,开挖中的较多成果仅能反映一个环节,因而用应力状态分析模量回复应是初步的,为的是揭示高重力坝坝基岩体模量的回复、提高,为今后科学、合理地开展坝基固结灌浆提供参考资料,也为以后的分析、研究提出另一种研究方法。
选取河床部位一条主断面线作代表性分析(图17),计算高程从河床表面(海拔高度 1 200 m)至河床下部100 m左右,深度约200 m,建基面(海拔高度 1 163 m)以下深度170 m左右。
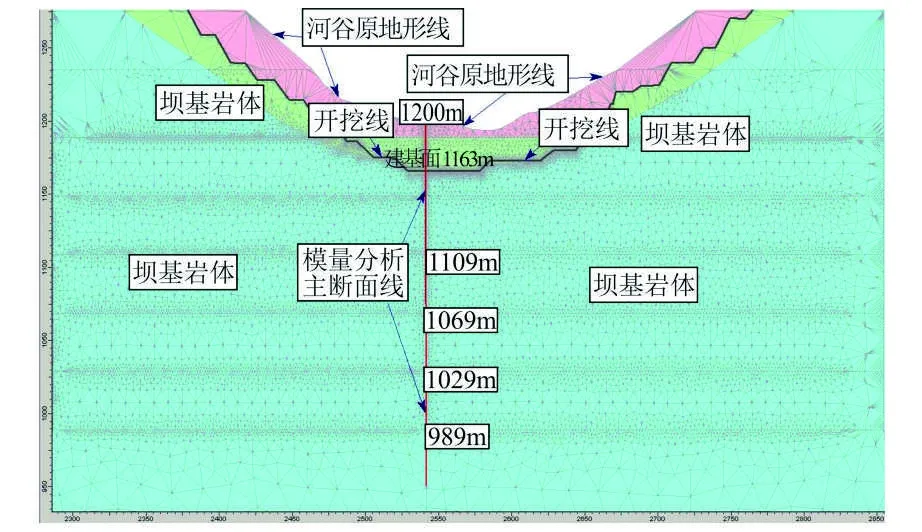
图17 模量回复力学研究计算主断面线位置Fig.17 Position of major cross-section line in research of mechanical calculation of modulus recovery
6.1 开挖前河床岩体模量分析
为分析坝基开挖前岩体模量,仍采用均化的方法,即以岩级代表含有硬性结构面,包括小的弱面的不均匀岩体。官地坝基无大的弱面。计算模量按前面的模型。
表4为用平均应力、体积应变资料计算的未开挖前河床部位岩体不同深度的变形模量(为了简化,表中仅列出部分单元),资料表明:①河床浅表部(海拔高度 1 200.63~1 164.26 m),按平均应力、体积应变计算的岩体变形模量平均值为 3 203 MPa,属于Ⅳ级岩体。②海拔高度 1 163.93~1 159.87 m,计算的岩体变形模量平均值为 8 915 MPa,属于Ⅲ1级岩体;海拔高度 1 163 m为建基面,按规范要求,可以作为高重力坝坝基,计算的模量与原来选定的建基面要求的模量是吻合的。③海拔高度 1 158.86~988.72 m,计算的坝基岩体变形模量平均值为 17 198 MPa,属于Ⅱ级岩体,模量值与地质上建议的变形模量大致相同。

表4 开挖前河床岩体变形模量Table 4 Deformation modulus of rock mass at riverbed before excavation
计算的坝基岩体变形模量与建基面选取的变形模量值相符,和建基岩体的变形模量值大致相同,表明用力学方式进行评价是可行的,因而可以作为坝基开挖后和重力坝修建后坝基岩体变形模量分析的基础。
6.2 坝基开挖后河床岩体变形模量分析
表5为计算的坝基开挖后河床岩体的变形模量。由于开挖后河床岩体应力状态发生变化,应力集中包向下转移,计算的岩体变形模量出现降低:①表部2 m左右(海拔高度 1 163.93~1 161.91 m),相当于爆破松弛带,岩体变形模量为 3 682.7~4 346.1 MPa,平均值为 4 033 MPa,属于Ⅳ级岩体的变形模量。②浅部2~10 m深度(海拔高度 1 160.89~1 141.44 m),岩体变形模量由原来的12~17 GPa变为5~7 GPa,降低幅度较大,其原因是应力集中包向下转移,建基面下由原来的应力集中包位置变成应力较小的部位,而应力较高的部位在海拔高度1 120 m左右。

表5 计算的开挖后河床岩体变形模量Table 5 Calculated deformation modulus of rock mass at riverbed after excavation
6.3 混凝土重力坝修建到设计的高度时坝基岩体变形模量的回复
表6为官地重力坝修建到设计的高度时河床岩体变形模量和开挖前、开挖后河床岩体的变形模量。表中资料表明:①重力坝压重后河床岩体变形模量有了较大回复;建基面(海拔高度 1 163.93~1 141.44 m)平均变形模量为14.3 GPa,较开挖后的4.8 GPa有了较大的变化;建坝后、开挖前平均模量14.3 GPa、14.1 GPa,岩体变形模量回复到开挖前的量值(表中的平均值)。②海拔高度 1 139.62~1 032.35 m段,建坝后、开挖后、开挖前河床岩体的变形模量分别为19.28 GPa、10.98 GPa、17.54 GPa,建坝后的变形模量比开挖前高出1.74GPa,这与高171 m坝体在该处高出原地表(海拔高度 1 200 m)134 m的压重有关;而高出开挖后平均模量近8 GPa(表6)。③海拔高度 1 030.53~988.72 m,建坝后、开挖后、开挖前计算的河床岩体变形模量平均值分别为14.11 GPa、11.12 GPa、17.19 GPa,岩体模量没有回复到开挖前的量值,这与河床应力集中包的转移、应力变化有关,但变形模量较开挖后提高了3 GPa。
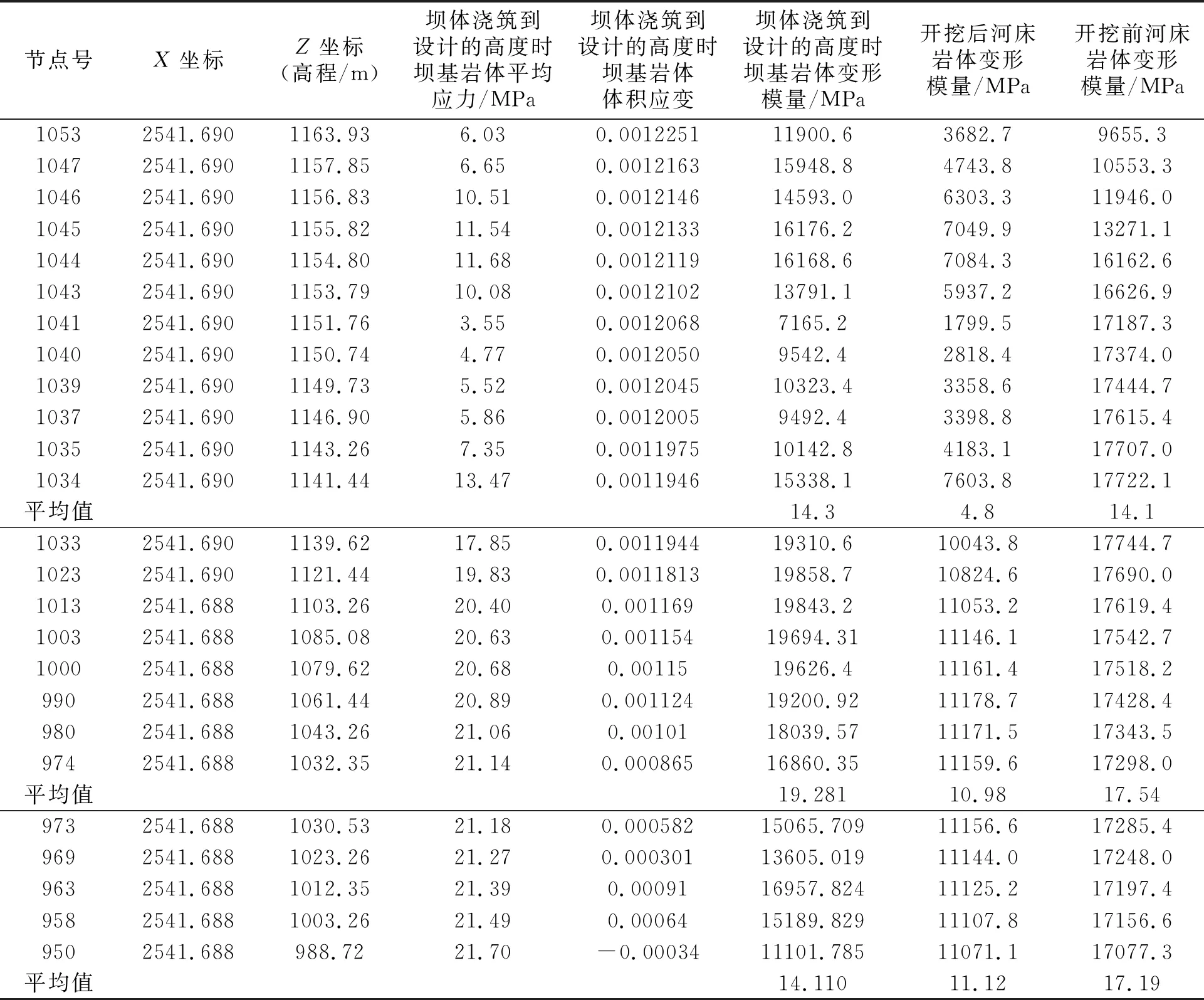
表6 计算的坝体浇筑到设计的高度时坝基岩体变形模量Table 6 Calculated deformation modulus of rock mass when dam foundation poured to dam crest
7 结 语
高混凝土重力坝大多以微新、弱风化下带的坚硬岩体作为坝基,河床表部的岩体大多不能达到这一条件,因此需要进行较大范围、较大深度的爆破开挖,挖除强风化、弱风化上带的岩体,从而引起岩体的松弛、卸荷,导致变形模量降低,成为高重力坝坝基重大工程问题。本文以概化的地质模型,以力学的基本方程和数值分析研究了官地水电站坝基玄武岩体在开挖前、开挖后和坝体浇筑后坝基岩体变形模量的变化及特征,得到以下结论及认识:
a.基于弹性力学理论研究高混凝土重力坝坝基岩体变形模量的变化应深入分析河谷的应力状态,给定的岩体力学参数应尽可能的合理,坝址地质结构模型应尽量精细。
b.本文以建立的岩体模量计算的理论公式为基础,以较精细的地质结构模型、较为准确的力学参数为前提,以数值分析为方法,研究了官地水电站河床坝基岩体随坝基开挖应力的降低、松弛回弹,建基面附近岩体变形模量由原来的14.1 GPa降低到4.8 GPa;随高重力坝重量的加载,坝基岩体被压密,变形模量达到14.3 GPa,发生回复,这为高重力坝坝基变形分析,提供了另一种研究途径。
c.本文用应力状态分析高重力坝坝基岩体变形模量的回复应是初步的,为的是揭示高重力坝建成后坝基岩体变形模量出现的回复、提高,为今后科学、合理地分析高重力坝坝基岩体力学参数提出了另一个研究思路。

