公共部门临聘人员岗位规模管理与控制模型建构——以深圳市罗湖区为个案的研究

王怡然，郭远远

（中央司法警官学院，河北保定 071000）

一、问题提出

我国历来对公务员实行严格的编制管理。《中华人民共和国公务员法》第二十五条明确规定：录用公务员，必须在规定的编制限额内，并有相应的职位空缺[1]。编制包括人员的数量定额和领导职数，由各级编制管理机关依据职能配置和职位分类，按照精简的原则确定[2]。随着我国经济社会的健康快速发展和公众需求的日益多元化，不少地区和部门机关事业单位的编制人员出现了不同程度的缺口，难以胜任日渐繁重的社会事务管理工作。在这种形势下，我国各级机关事业单位均招聘了大量临聘人员来承担一些岗位工作。

所谓临聘人员，是指由政府通过公共财政临时聘用，并协助政府部门或事业单位从事公共管理活动或行政事务的，不列入政府编制的人员[3]。这一特定群体通常是（街道）机关事业单位因工作需要，聘用于专业技术、辅助管理、工勤服务等岗位工作的人员[4]。其最大的特点就是不在公务员编制之内，即所谓的“编外人员”，通过签订劳动合同，其与用人单位之间形成一种临时的聘用关系，聘期根据聘用岗位的实际工作任务确定，合同期满需视工作需要并经考核合格才能续签合同。在实践中，我国公共部门临聘人员制度大大缓解了正式编制的不足，在我国各级政府，尤其是基层政府管理社会事务中发挥了一定的积极作用，但是由于管理不够规范，该制度还存在着不少弊端。例如缺乏科学的制度规范和监控机制、入口管理较混乱、执行公务的主体合法性受到质疑等等；部分临聘人员素质不高、效率低下、态度恶劣甚至是违法乱纪现象屡见报端，引起公众诸多不满。与此同时，由于同工不同酬，工资福利待遇偏低，工作量大，加之缺乏有效激励机制及职业发展前景，临聘人员怨声载道，离职率也比较高。要想破解上述难题，就必须对我国机关事业单位临聘人员实施科学管理，而首要工作是合理确定临聘人员的岗位规模。

深圳市罗湖区是实施临聘人员制度的代表性地区，截至2017 年3 月，该区临聘人员数（含编外和挂企借用人员）达到了32 264 人。在员额规模构成中，街道一级临聘人员员额规模占据较大份额，而且上升趋势远远超过公安、教育、卫生等其他系统。自2010 年以来，罗湖区街道临聘人员员额规模绝对增长值为4 583，占到该区临聘人员员额总体增长规模的81.27%；年均增长率约为10.84%，远高于该区临聘人员员额规模的增长速度。由此可见，罗湖区临聘人员员额规模压力主要来自街道一级。因此，本文主要对罗湖区街道一级临聘人员员额规模及其主要影响因素调查研究的基础上，通过回归分析，构建综合模型，以对临聘人员的岗位规模实施管理与控制。

二、研究依据

（一）样本选取

本文选取深圳市罗湖区的五个典型街道作为一级抽样对象，将调研对象定位于政府官员、临聘人员与社区居民三个群体，确定每个群体的抽样规模。而后采取等距抽样法，分别在五个街道抽取以下样本数量（见表1）。

表1 各街道问卷选样群体结构分布

（二）数据获取

本文主要通过实地问卷调查获取一手数据。在罗湖区各街道办的大力支持下，问卷得以顺利发放和回收，具体情况如表2 所示。在问卷调查过程中，结合深度访谈、历史文献调查等方法，全面获取数据与资料。

表2 问卷发放与回收情况

（三）变量选取

根据调研资料分析，我们设定影响罗湖区临聘人员规模的主要指标包括以下11 项因素：户籍人口规模、管理与服务人口规模、社区个数、地区生产总值、全社会固定资产投资总额、人均生产总值、财政收入总额、一般预算收入总额、一般预算总支出、一般公共服务支出、辖区面积平方公里数。这些指标构成临聘人员岗位规模这一目标变量（又称为因变量或被解释变量）的预测变量（又称为自变量或解释变量）。

（四）分析方法

主要运用SPSS 17.0 版分析软件工具对获取的数据资料进行录入和分析[5]。为了了解哪些因素对临聘人员岗位规模这一变量具有影响力和预测力，通常的做法是先进行皮尔森积差相关分析，再进行回归分析。在此基础上，构建多元回归模型，最终实现对研究对象进行预测和控制应用。但是在实际操作过程中，我们发现个别重要的常识性影响变量，比如辖区区划面积等相关变量，尽管在相关分析中显示出高度显著相关关系，但经过回归分析之后最终却没有被纳入回归方程中来。因此，为避免分析结论产生结构性系统错误，咨询专家后，本文最终选择采取非常规的分析思路，即经由调研数据分析，结合专业常识和深度访谈资料，确定出有关罗湖区各街道临聘人员岗位规模的可能解释变量之后，不经由皮尔森积差相关分析阶段，而是直接对所确定的解释变量与被解释变量进行逐步回归分析，以求得回归模型解。由于该分析方法更加强调专业知识、调查问卷等多方面数据资料的综合运用，故而权且可以称之为综合回归分析[6]。

三、模型的提出与检验

由于多数街道办所能提供的只有过去三至五年期间的历史数据，而罗湖区只有10 个街道，每一年的截面数据极其有限。为解决样本数据不足问题，本文以各街道办提供的“现有临聘人员岗位总数”的历史数据完整度为依据，将各个街道办近年来的数据一并汇总，形成一个综合数据文件。在此基础上，对所形成数据文件进行横截面分析处理，而不是纵贯性的时间序列研究。

将选取出的11 个自变量与“现有临聘人员位总数”这一被解释变量进行皮尔逊积差相关分析，找出与临聘人员岗位规模有显著相关的因素。由表3 可知，被解释变量与7 个自变量之间存在不同程度显著相关关系。

表3 现有临聘人员岗位总数与自变量间相关性检定

第一，“现有临聘人员岗位总数”与“管理与服务人口规模”“社区个数”“财政收入总额”“一般预算收入总额”“辖区面积平方公里数”等几个变量之间存在着p<0.01 的高度显著相关关系，而与“全社会固定资产投资总额”“一般预算总支出”等两个变量之间存在p<0.05 的显著相关关系。

第二，“现有临聘人员岗位总数”与“管理与服务人口规模（辖区总人口）”“社区个数”“全社会固定资产投资总额”“财政收入总额”“一般预算收入总额”“一般预算总支出”等几个变量之间存在显著正相关关系，而与“辖区面积平方公里数”之间具有显著负相关关系。由此，分析剔除了“户籍人口”“地区生产总值”“人均生产总值”“一般公共服务支出”4 个与因变量之间不存在显著相关关系的影响因素。

对于上述7 个预测自变量，我们采取逐步回归分析方法，共形成了一元线性、二元线性、三元线性回归模型各一个（见表4）。最终，“管理与服务人口规模”进入了一元回归模型；“管理与服务人口规模”“辖区面积平方公里数”两个变量则进入了二元回归模型。“管理与服务人口规模”“辖区面积平方公里数”“一般预算收入总额”三个变量则进入了三元回归模型。其中，三元回归模型的决定系数最高，该回归模型的决定系数R2=0.797，这表明，该模型对总平方和的解释能力达到79.7%，本文将其作为此次分析的优选模型。

表4 模型汇总

由表5 可知，在所形成的三元回归模型中，模型检测统计量F=40.584，p=0.000<0.001，因此，该模型具有高度显著性。又由表6 可知，在所生成的三元线性模型中，除了“常数项”外，“管理与服务人口规模”“辖区面积平方公里数”“一般预算收入总额”等三个变量的参数值分别为0.002、4.102、0.016，检测统计量t 值分别为6.215、2.459 与2.433，都较大，且各自p 值分别为0.000、0.020 和0.021，皆小于0.05的显著性水平。这表明，在置信度为95%的水平上，“管理与服务人口规模”“辖区面积平方公里数”“一般预算收入总额”等三个解释变量对临聘人员岗位规模的影响是显著的。

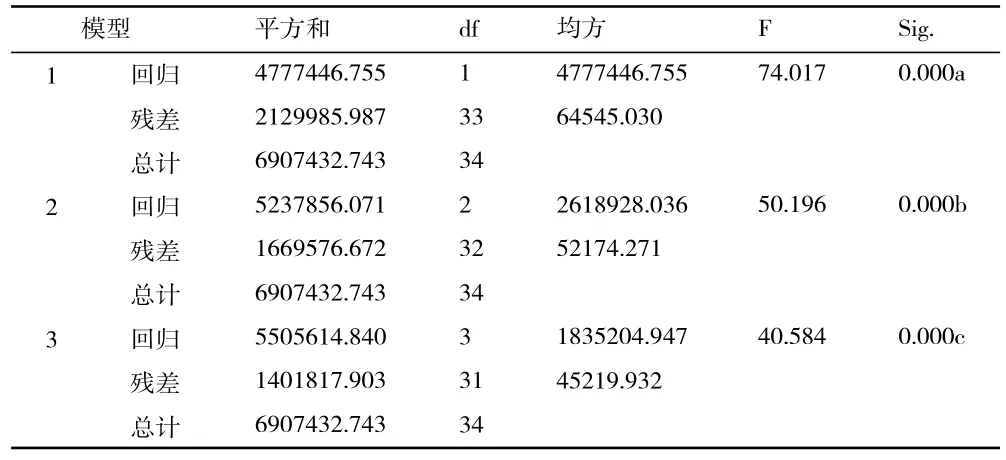
表5 Anovad

由此，我们得到回归方程式I：

临聘人员岗位总数（LP）=-184.213+0.002* 管理与服务人口规模（MP）+4.102*辖区面积平方公里数（RS）+0.016*一般预算收入总额（BI）

进一步检测各自变量之间的容忍度与方差膨胀因子（VIF）等数值，由表6 可知，各自变量之间的容忍度在0.385 以上，方差膨胀因子数值低于2.60，基本可以排除共线性的疑虑。由此可以推论，此次分析所形成的三元线性回归模型对于罗湖区临聘人员岗位规模的发生具有较为显著的解释能力。

表6 系数a

四、回归模型的预测区间与测算公式

（一）预测区间测算与运用

通过计算被解释变量预测值的置信区间或说预测区间，可以对临聘人员岗位规模进行员额上下限的预测控制。在进行预测时，一般有两种不同的置信区间测算法，一个是“均值（mean）的置信区间”，另一个为“个值（individual）的置信区间”，“个值预测”的置信区间宽度往往比“均值预测”的置信区间大。因此，本文选择以相对更为精准的“均值预测”来推算因变量的置信或预测区间。具体地，在置信度为95%的水平下，罗湖区各街道2017 年临聘人员岗位规模预测区间上下限数值和实有员额数值详细的数据结果如表7 所示。

表7 临聘人员岗位人数上下限控制

从表7 可知，除了黄贝由于缺乏关键变量“一般预算收入总额”而无法进行测算之外，各街道办2017 年临聘人员岗位规模呈现以下特征：

（1）大部分街道临聘人员岗位规模都在信度为95%的置信区间之内。其中，东晓、南湖、笋岗、东湖、莲塘等5 个街道2017 年的临聘人员岗位规模都在这一置信区间之内。简言之，在能够进行测算的9 个街道中，将近56%的街道临聘人员岗位规模都在预测控制区间之内。

（2）桂园、东门、翠竹、清水河等4 个街道办都属于临聘人员员额规模超标的地区。清水河、桂园街道的超标程度较低，分别在1.2%和3%；翠竹和东门街道的超标情形较为严重，超标程度分别达到25.6%和30%。

（二）点估计测算与运用

进一步将各个街道办2017 年的数据代入回归方程式中，得到的预期值（也称为点估计值或理论值），然后，再计算预期值与实际值（也称为观察值）之间的差值，并将相关数值列成表，如表8 所示。

从表8 可知，运用回归方程式（I）进行计算，考虑管理与服务人口规模、辖区面积平方公里数与一般预算收入总额等三个自变量，则深圳市罗湖区9个街道的临聘人员全部超额，共计超标1 749 个员额。因此，结合公共部门岗位编制与员额管理专业理论和我国公共组织运行实践经验，可以推论，本研究所构建的临聘人员岗位规模三元线性回归模型能比较准确地反映公共部门人员配置的管理与控制要求。

表8 临聘人员岗位实际人数与理论人数差异表

需进一步说明的是，本研究以深圳市罗湖区街道一级临聘人员员额规模为个案所构建的回归模型可以较为准确地解释罗湖区街道一级临聘人员岗位规模及其变动规律。实际操作中，关于公共部门临聘人员岗位规模的配置还应结合不同地区社会管理工作现状与实践要求来进行，需由相关决策部门综合考虑各方面实际情况在控制区间内确定临聘人员具体岗位数值。同时，在总体条件不发生重大变化的情况下，本研究还可为其他地区临聘人员岗位规模变动提供较为精确的数理基础，为政府决策部门进一步加强街道临聘人员员额动态管理、核定员额规模提供借鉴依据。