基于GA 优化灰色神经网络模型的建筑业增加值预测研究
光辉
通过建筑业增加值指标可以了解建筑业的生产规模、发展速度、经营成果,并为国家制定经济建设计划提供依据,因此,预测建筑业增加值有一定的现实意义。近年来,诸多研究者构建一元线性回归模型、ARIMA 模型、灰色模型、BP 神经网络模型、系统动力学模型等对建筑业总产值进行预测,其中灰色模型因建模信息少、运算方便被广泛使用,但同时存在预测精度低、长期内不可预测的缺点,基于此,本文将灰色理论和神经网络理论进行组合,并采用遗传算法(genetic algorithm,GA)的优化模型的初始权值和阈值,构建GA 优化灰色神经网络的建筑业增加值预测模型,并利用该模型对我国建筑业增加值时间序列进行预测,验证其适用性和有效性。
1.灰色神经网络模型GM(1,1)-BP
灰色系统模型能够利用少量数据迅速建立预测模型,神经网络模型在处理波动序列数据方面有很强的自适应能力。灰色神经网络模型综合了灰色系统模型和BP 神经网络模型各自优点而建立的一种组合预测模型,运用灰色系统理论建立建筑业增加值时间序列的残差模型,利用残差序列对BP 神经网络进行训练,利用训练网络进行预测,文献利用该模型进行时间序列分析,结果表明模型在小样本、贫信息和波动序列等情况下可以进行比较准确的模拟和预测[1]。
1.1 建立预测模型

求解微分方程,得GM(1,1)预测模型:
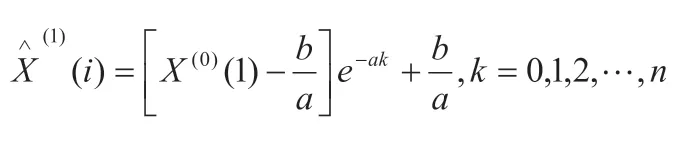
1.2 建立残差序列

1.3 求解新的预测值
利用训练好的网络预测残差值,则新的预测值为:
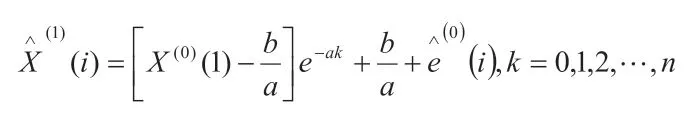
2.建立模型
取我国建筑业增加值1999 年~2016年统计数据,构建灰色系统模型,构建残差序列,运用残差序列训练BP 神经网络模型,构建GA优化灰色神经网络模型,并对2017 年~2019 年建筑业增加值进行预测。计算结果如表1、表2 所示。
3.结果分析
通过表1、表2 可以看出,GM(1,1)模型模拟最大绝对误差值为-8.952百亿元,最大相对误差为31.11%,模拟值相对误差平均值为13.3%,相关系数R2为0.9751,模型预测最大绝对误差为-16.964 百亿元,最大相对误差为24.12%;GA-GM(1,1)-BP 模型模拟最大绝对误差值为-2.976 百亿元,最大相对误差为29.71%,模拟值相对误差平均值为4.7%,相关系数R2为0.9961,模型预测最大绝对误差为-6.894 百亿元,最大相对误差为,9.72%。从上述数据可以看出,GA-GM(1,1)-BP 模型能够有效提高预测精度。
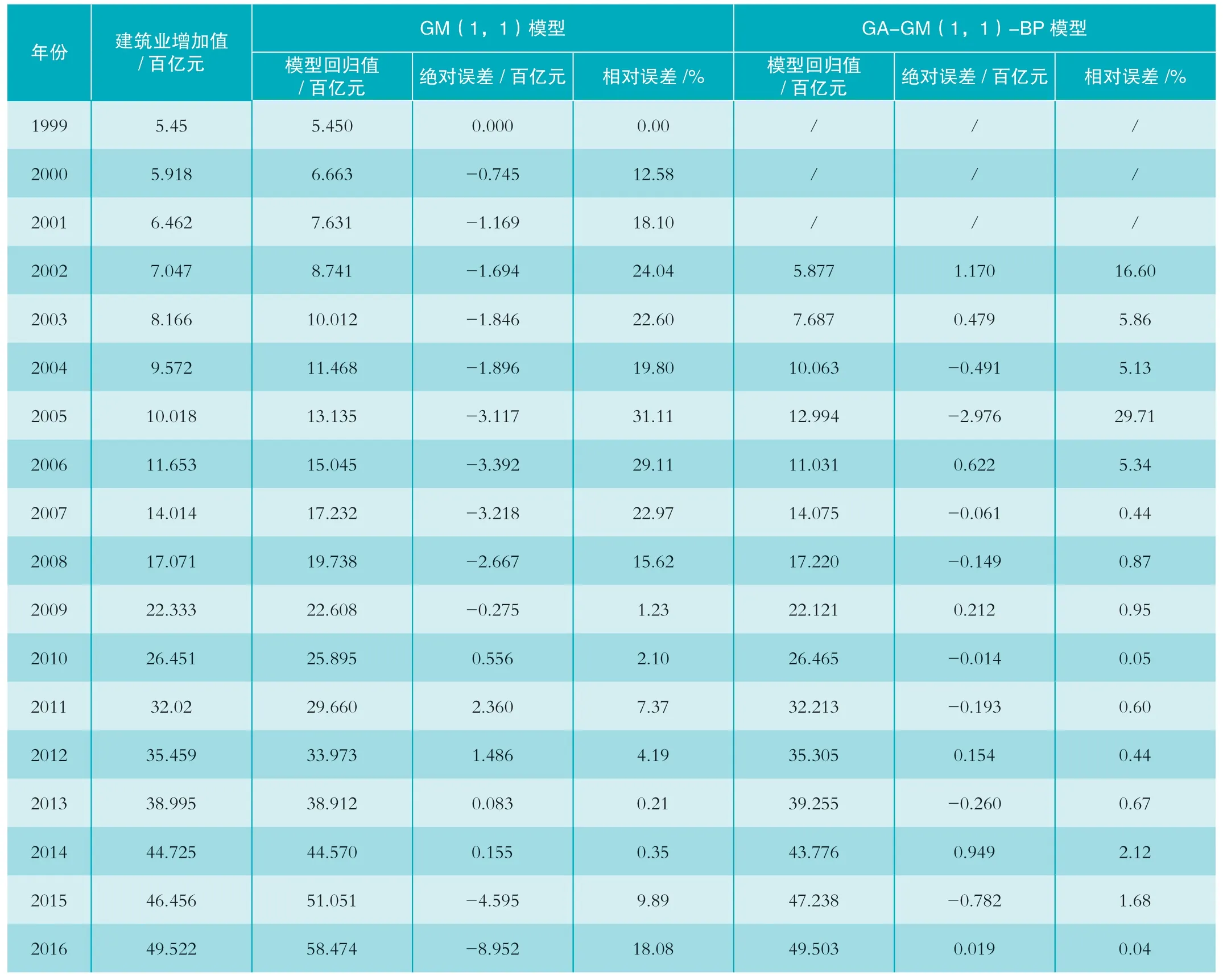
表1 GM(1,1)模型与GA-GM(1,1)-BP 模型回归值对比
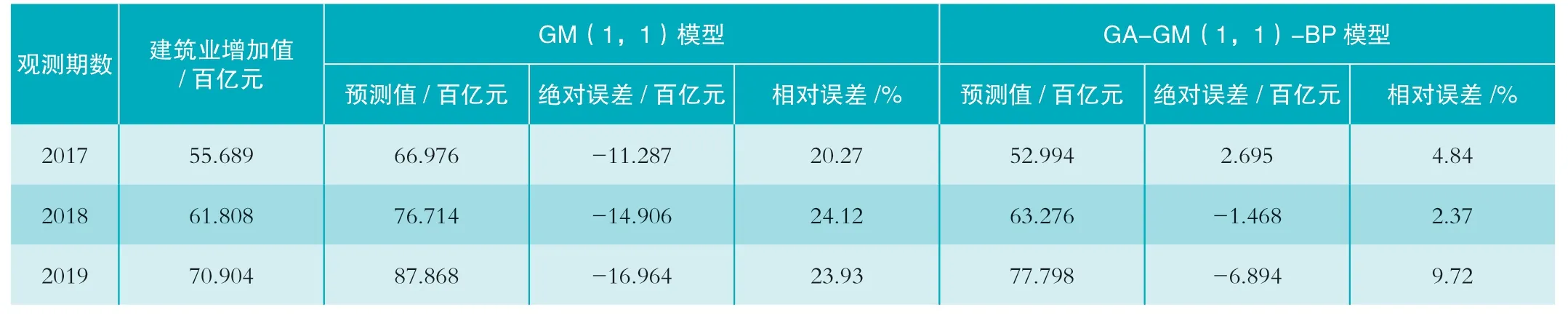
表2 GM(1,1)模型与GA-GM(1,1)-BP 模型预测值对比
4.结论
(1)采用经过遗传算法优化的灰色神经网络模型来预测建筑业增加值,误差小,收敛速度快,证明该模型与方法分析此类时间序列数据有较好的适用性和准确性。
(2)GA-GM(1,1)-BP 模型精度在很大程度上依靠训练样本的数量,训练样本越多,预测精度就越高,应该及时将新的监测信息添加到训练样本中,及时更新模型以得到更好的预测效果。

