一种姿态测量系统的FPGA和DSP设计与实现
吕金锐

摘 要: 为了实现对某弹载系统的姿态测量,提出一种基于FPGA+DSP的姿态测量系统的设计。系统采用FPGA作为逻辑控制核心,完成对MEMS传感器输出的陀螺加表数据的采集,并通过EMIF接口完成与DSP的数据通信。DSP完成对姿态信息的解算,并由FPGA通过RS422接口将更新后的姿态信息上传至上位机。系统选用地理坐标系作为导航坐标系,利用四元数法及Kalman信息融合算法对采集到的姿态信息进行解算。测试结果表明,该系统输出的姿态信息精度较好,总体角误差在0.5°以内。
关键词: MEMS传感器; 姿态测量; FPGA+DSP; 四元数; Kalman信息融合; 姿态解算
中图分类号:TN702 文献标识码:A 文章编号:1006-8228(2021)05-29-04
Design and implementation of FPGA and DSP for attitude measurement system
LV Jinrui
(Department of Information Engineering, Taiyuan City Vocational college, Taiyuan, Shanxi 044000, China)
Abstract: A kind of attitude measurement system based on FPGA and DSP is proposed to realize the attitude measurement of a projectile-borne system. The system uses FPGA as the core of logic control to collect the gyro table data output by MEMS sensor and to communicate data with DSP through EMIF interface; The DSP completes the resolution of the attitude information, while the FPGA uploads the updated attitude information to the upper computer through the RS422 interface. Geographic coordinate system is chosen as navigation coordinate system, and the attitude information collected is solved by Quaternion method and Kalman information fusion algorithm. The test results show that the accuracy of attitude information output by the system is good, and the overall angle error is within 0.5.
Key words: MEMS sensor; attitude measurement; FPGA and DSP; Quaternion; Kalman information fusion; attitude resolution
0 引言
姿態解算作为姿态测量系统中的核心部分,正朝着高精度和高速度的方向发展[1]。为实现更加准确的对弹载系统的姿态测量,不仅对数据的采集及处理算法提出更高的要求,同时对于处理器的选择也越来越重视。在测量系统中,确定姿态主要运用的是陀螺,但由于陀螺仪长期工作存在精度测量漂移从而无法保证系统精度,对姿态的确定会产生很大的偏差[2]。针对以上问题,系统采用ADIS16488传感器为核心,结合FPGA的并行处理方式以及DSP强大的数据处理能力,构建了一个姿态测量系统。
1 系统总体设计
系统采用美国AD公司产品ADIS16488 MEMS惯性传感器作为核心,其内部集成了三轴微陀螺仪,三轴微加速度计,三轴微磁强计以及压力传感器[3]。当MEMS惯性传感器处于工作模式时,能够同时采集三个轴向上的加速度、角速度及磁强度。
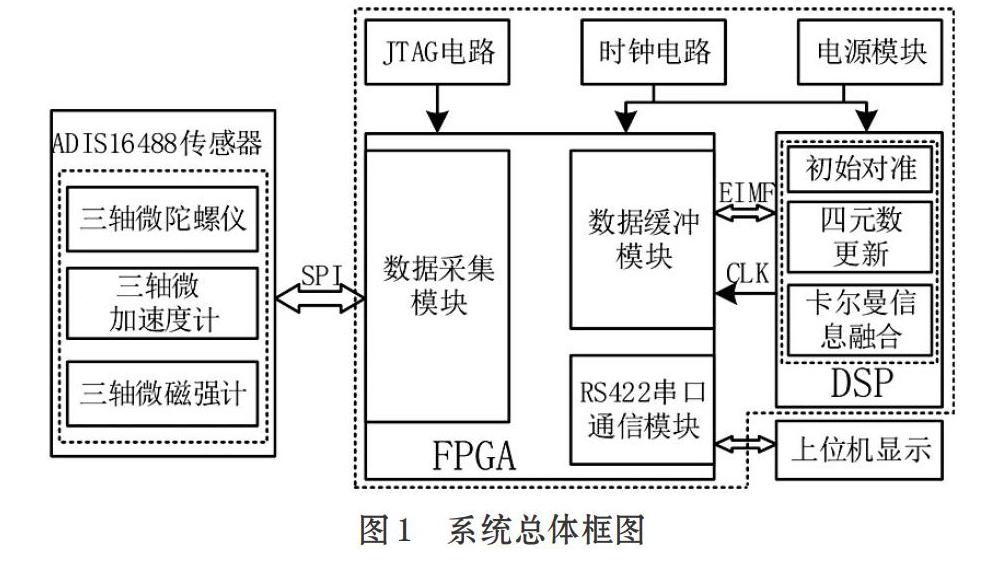
系统总体结构图如图1所示。系统工作原理:FPGA作为主控芯片,首先通过SPI接口对传感器进行初始化配置,然后根据上位机指令采集传感器输出的陀螺加表等数据至数据缓冲模块,通过EMIF接口将数据传输至DSP进行数据处理,最后将解算好的姿态信息通过RS422发送模块上传至上位机进行显示。
2 硬件电路设计
2.1 传感器数据采集模块
惯性测量单元正常工作时,需加载3.3V电压至10、11、12引脚[4]。上电后,系统首先通过FPGA完成对传感器的初始化配置,然后SPI接口来读取更新后的传感器数据。传感器内部寄存器采用分页结构,每一页都对应其相应的功能[5]。FPGA对MEMS传感器进行读写时需要连续两个8bit地址进行操作,其中低地址在前,高地址在后。高8bit地址表示传感器内部相应寄存器的地址,低8bit地址表示写入该寄存器的数据内容。如图2所示,对传感器进行读操作时需要一个16bit的寄存器地址,且相应寄存器地址上的数据输出将在下一个寄存器地址输入时才会输出。
2.2 FPGA与DSP通信接口设计
FPGA与DSP通过EMIF接口来实现通信,如图3所示,EMA_DATA[15:0]为数据总线,EMA_WE为FIFO读使能信号,GPIO4_15为启动数据发送信号,EMA_CS为EMIF使能信号。为匹配数据传输速率,采用双端口RAM来对读取的DSP数据进行缓存,在双端口RAM模块和DSP模块之间串联33Ω电阻来减少信号失真[6]。双口RAM发送模块不仅实现了数据的读写独立,也满足了数据在发送时间上的要求。
3 姿态解算算法
3.1 初始姿态对准
在求解载体姿态前对系统进行初始对准,对于提高姿态信息精度有很大的影响。首先利用载体在地理坐标系的投影[00gT]和在载体坐标系的投影[fxbfybfzbT],得出载体横滚角和俯仰角,然后利用求得的初始横滚角和俯仰角计算初始航向角[7]。算法推导过程如下:
[fxbfybfzb=Cnb00g]=[cosγcosγsinθ-sinγcosθ0cosθsinθsinγ-sinγsinθcosγcosθ][ 00g]
求解得初始横滚角和俯仰角:
[θ=sin-1][fyb/g]
[γ=tan-1-fxb/fzb]
结合磁强计由载体坐标系映射到磁场x、y方向上的值,求解得:
[Hx=mxcosθ+mysinγsinθ+mzcosθsinγ]
[Hy=mycosγ-mzsinγ]
然后求得初始航向角:
[ψ=arctanHy/Hx]
3.2 四元数法
根据欧拉定理可知,载体坐标系b相对于地理坐标系n的方位相当于b系绕定轴转动3次方位角,四元数包含了转动的信息[8]。[un]为旋转轴和旋转方向,θ为转过的角度。
[Q=cosθ2+unsinθ2]
利用哥式等式推导得出四元数的微分方程为:
[Q=12Q?ωbnb]
矩阵形式为:
[T0T1T2T3=0-ωx-ωy-ωzωx0ωz-ωyωyωz-ωzωy0ωx-ωx0]
然后利用四阶龙格库塔法求得四元数更新表达式:
[k1=T2ωbt?qt]
[k2=T2ωbt+T2?qt+k12]
[k3=T2ωbt+T2?qt+k22]
[k4=T2ωbt+T2?qt+k3]
[qt+T=q(t)+][T6][k1+2k2+2k3+k4]
四元数可确定出载体坐标系到地理坐标系的坐标转换公式:
[Cnb=q20+q21-q22-q232q1q2-q0q32q1q3+q0q22q1q2+q0q3q20-q21+q22-q232q2q3-q0q12q1q3-q0q22q2q3+q0q1q20-q21-q22+q23]
3.3 卡尔曼滤波
卡尔曼滤波的主要作用在于最大限度的减小噪声目标信号的影响,利用不同时刻的系统状态信息,对信息预测和估计,最终得到一个较为精确的数值。它相当于一个动态递归的过程:
[Xk=AkXk-1+Bkuk-1+wk-1]
[Zk=HkXk+vk]
其中,Xk为k时刻的系统状态,Zk表示k时刻的观测变量。uk为K时刻对系统的控制量。vk,wk分别表示状态方程的观测噪声和过程噪声。Hk是观测噪声误差状态增益矩阵,Ak和Bk是系统参数[9]。
卡尔曼滤波的时间更新公式为:
[X-k=AXk-1+Buk-1]
[P-k=APk-1AT+Q]
由k-1时刻的最优值[Xk-1]去预测k时刻系统的状态值[X-k]。然后由上一次的误差协方差[Pk-1]和过程噪声Q预测新的误差[10]。
卡尔曼滤波的状态更新公式为:
[Kk=P-kHTHP-kHT+R-1]
[Xk]=[X-k+KkZk-HX-k]
[Pk=I-KkHP-k]
计算卡尔曼增益Kk,并进行校正更新,得到的[Xk]即为k时刻的最优估计值。为下一步估计k+1时刻的最优估计值的迭代进行更新操作,即更新Pk。
3.4 小波阈值降噪
由于ADIS16488内部的MEMS陀螺仪的抗干扰能力较弱,产生的噪声相对于其他两个传感器而言更大。因此系统结合陀螺仪输出信号不具备线性的特点,选用小波阈值降噪算法来对进行降噪处理。小波阀值消噪原理如图4所示。
系统进行了对静置的传感器进行了降噪实验,系统上电后对陀螺仪y轴数据进行采集,采样频率为200Hz,采样时间为100s,得到陀螺仪的实时数据如图5所示。
由图5可以看出,当陀螺仪静置时,其y轴输出的角速率误差值较大,范围在[-0.04°,-0.04°]。对该陀螺仪采用小波阈值降噪处理后,得到如图6所示的误差波形图。由图6可以看出,陀螺仪静置时y轴输出的波形有了明显的改善,角速率误差约束到了[-0.02°,-0.02°]。
4 系统测试
4.1 传感器數据采集模块仿真
传感器输出的数据对于整个测量系统来说有着十分重要的作用,它关乎着数据的正确性和完整性。FPGA负责接收传感器输出的数据并将其缓存至内部RAM中,同时也负责读出DSP解算后缓存至RAM中的数据,并将其上传至上位机。为了验证FPGA与DSP之间通信的正确性,将在FPGA RAM中写入数据0-256,DSP通过EMIF接口读取RAM中的数据,在开发环境ISE下显示DSP读取的数据以及其他信号的一些变化,它读取的数据地址空间是从0xc0000000开始。如图7所示,DSP与FPGA之间通信正确。
4.2 误差分析
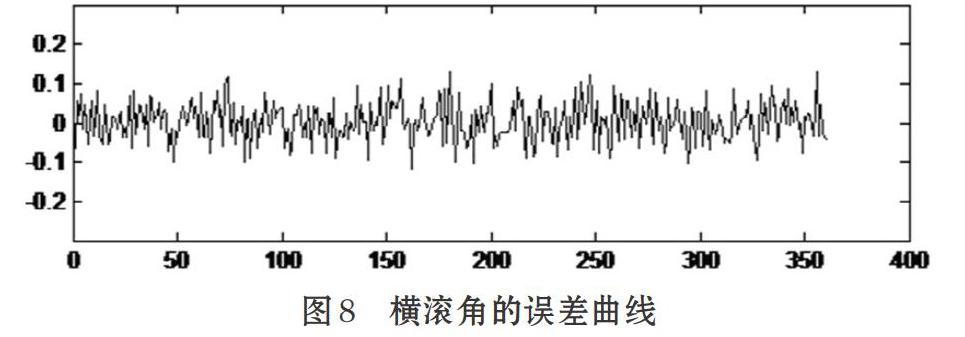
为了对系统性能进行测试与验证,采用AHRS(商业级姿态参考系统)作为参考。验证过程中,将该参考系统与电路板固定,并置于三轴无磁转台中。未上电之前调整轴向,使得系统坐标系和转台的轴向一致。以z轴为定轴进行5°/s的转动,采集时间为360s,数据采集完成后通过串口上传至上位机。上位机对接收到的数据进行分析计算,采用Matlab对接收到的数据进行曲线显示,如图8、图9、图10所示。
由于系统在进行测试时选用z轴为定轴进行转动,从得到的误差曲线图中可以看出,横滚角和俯仰角的误差较小,均在0.4°以内,姿态解算精度较好。即验证了系统在转动过程中,x轴和y轴方向的姿态没有发散。
将系统姿态解算的结果与AHRS测量的数据进行比较,得出其误差的标准差,如表1所示。验证系统解算的结果较好,误差值均在0.5°以内。
4.3 上位机数据显示
系统通过RS422接口将解算好的姿态信息发送至上位机进行显示,如图11所示。图11为传感器绕z轴转动时,三个轴向角度的变化曲线图。如图12所示,可以直观的看到传感器的全姿态信息。
5 结束语
系统采用FPGA+DSP双处理器的方案来实现对某弹载控制器的姿态解算,通过系统测试,验证该姿态测量系统的输出精度较好,均在0.5°以内,能够满足技术要求。这为后续测量系统的进一步优化提供了可靠的实验数据。
参考文献(References):
[1] 沈怀营,吴伯衣.基于DSP/FPGA的高速旋转体姿态角及转速的解算系统设计[J].山西电子技术,2012.3(1):41-43
[2] 李炳炳.基于MEMS惯性传感器的人体姿态检测系统的研究[D].南京理工大学,2017.
[3] 杨阳.基于ADIS16488 MEMS惯性组合姿态测量设计与研究[D].中北大学,2015.
[4] 廖文平.基于MEMS传感器的姿态解算的FPGA实现[D].长沙理工大學,2015.
[5] 李越.四旋翼无人机姿态解算及控制研究[D].昆明理工大学,2017.
[6] 张锐.基于FPGA的小型捷联式惯性导航系统研究[D].中国民航大学,2014.
[7] 杨兆静.基于FPGA的载体姿态角解算算法的研究与设计[D].燕山大学,2013.
[8] 杨龙,李范鸣.DSP EMIF与FPGA双口RAM高速通信实现[J].现代电子技术,2016.37(13):10-13
[9] 文雨辰.基于FPGA+DSP架构的GPS接收机设计和实现[D].电子科技大学,2010.
[10] 张荣辉,贾宏光.基于四元数法的捷联式惯性导航系统的姿态解算[J].光学精密工程,2008.16(10):1963-1970

