数据增强与序列分解在电价预测中的应用

李志强， 王凡凯， 刘曙元

(北京华电天仁控制技术有限公司，北京 100039)

0 引 言

随着我国电力体制改革的深入，部分区域在调频市场中，除常规发电单元外，第三方辅助服务提供者被鼓励参与到市场中来[1]。多样化主体促进了辅助服务市场化发展，同时市场主体对于报价等辅助决策的需求也日益增长。

目前改革处于前期阶段，竞价规则与政策随着市场化发展和运行结果反馈不断更新。因此针对某市场价格进行预测研究时，会发现该竞价规则下的市场运行时间较短，难以获取足够的数据量。一般以小时为单位的短期预测至少需要预测日前三周的历史数据，最好可提供历史三个月数据量。

另外调频出清价格受需求和气象等多种因素的影响，以大数据为基础的机器学习手段成为主流方法。然而针对受多种因素影响的目标而言，单一算法的泛化能力较弱，采用多种算法组合应用的方式可提升预测精度。

排序价格(Y排序)与报价(Y报价)的关系表达式为：

Y排序=Y报价/P

(1)

P=k/kmax

(2)

式中：P为发电单元归一化后的综合调频性能指标；k为归一化前的综合调频性能；kmax为所属调频资源分布区所有发电单元的指标最大值。

电价本身具有一定的波动性，而市场的出清方式将会加剧波动特性。如广东调频市场是根据调频里程排序价格进行顺序出清的，由式(2)可知分母P小于1，会导致排序价格波动性增强。因此如何准确预测价格的波动趋势是提升预测准确性的重点。

综上本文提出基于mixup数据增强和HHT(Hilbert-Huang transform)的电价组合预测方法，可改善数据量少和数据波动性大对于预测结果的影响，提高准确率。

1 mixup与HHT方法原理

1.1 mixup方法

mixup是由Zhang等人2018年提出的一种基于邻域风险最小化原则的数据增强方法[2]，用于图像分类及语音识别领域，文末对mixup是否能在回归预测领域发挥作用提出了期望。本文将对此进行验证。方法见式(3)。

(xn,yn)=λ(xi,yi)+(1-λ)(xj,yj)

(3)

式中：(xn,yn)为构建的新训练数据组;(xi,yi)和(xj,yj)为在原始训练集中任意抽取的两组不同数据。λ～Beta(α,β)，mixup方法应用时，β=α，α∈[0,+∞]，超参数α越大模型的泛化能力越强。

1.2 HHT方法

HHT可同时在时间和频率上表示信号的能量强度。具体方法如下：

(1) 对出清价格进行EMD(empirical mode decomposition)分解。得到多个IMF(intrinsic mode function)分量和余项[3]，将价格序列分解为不同特征波动的叠加。

EMD分解流程如图1所示。

图1 EMD分解流程

原始信号y′(t)经过EMD分解得到：

(4)

式中：IMFi为第i个IMF分量;RESn为余项。

(2) 对各分量进行Hilbert变换[4]，计算瞬时频率掌握频谱变化的规律。

(5)

从而y′的解析信号z(t)为：

(6)

各分量的瞬时频率f为[5]：

(7)

2 预测流程

2.1 数据收集与特征分析

(1) 梳理交易平台发布的信息，收集对应时段的气象数据，共N天的数据量。将出清价格记作目标项y，其他每一项记作一个特征项x。

(2) 将各特征项x分别与目标项y通过式(8)进行相关性指标r计算。当结果|r|>0.2时，标记该特征项为有效。

(8)

式中：Cov(x,y)为x与y的协方差;Var[x]为x的方差;Var[y]为y的方差。

2.2 数据处理

(1) 文本数据数值化得到数据集Data1。如02∶00数值化为2。截取Data1中前N-1日的数据记作原始训练集Data2。

(2) 采用mixup方法对Data2进行扩充得到数据集Data3。将Data1衔接于Data3之后得到扩充后的数据集Data4。

(3) 对Data4各特征项以及目标项通过式(9)分别进行归一化得到数据集Data5。

(9)

式中：z′为某一数据项归一化后的数据；z为归一化前的数据。

(4) 将Data5最后24组数据，即第N日归一化后的数据作为测试集Data5_1，其余数据作为新训练集Data5_2。

2.3 HHT分析

对Data5的出清价格进行HHT分析，针对频率值较高的高频分量，单一的预测方法往往效果不佳，选择集成算法模型；针对波动较小的低频分量采用神经网络算法模型。

2.4 模型训练

(1) 用Data5_2对各分量进行单独训练，保存训练过程模型。

① 对高频分量采用以决策树为弱学习器的GradientBoostingRegressor算法，它串行生成多个弱学习器，可以使得模型损失往负梯度的方向减少。另外决策树学习器本身不稳定，单颗树的方差较大，而在集成学习中，弱学习器间方差越大其泛化性能越好则集成学习模型的泛化性能就越好。

GradientBoostingRegressor算法训练流程如图2所示。

图2 GradientBoostingRegressor训练流程

② 神经网络算法较多文献描述，这里不予重复。

(2) 将Data5_2中的特征项输入各过程模型进行预测，当评价指标满足要求时结束训练，否则修改超参数继续训练。

2.5 预测

(1) 向训练好的各分量模型输入测试集Data5_1中的特征项，获得输出结果并反归一化得到Yi(i为模型数量)。

(2) 累加各项预测结果得到出清价格预测值Y[6]。

(3) 计算模型评价指标，对预测结果进行评价作为市场主体参与报价的参考。

3 预测算例

(1) 收集数据并进行相关性计算，得到与出清价格有关的有效特征项：时段、系统调频需求、温度和湿度四类特征项。

(2) 取α=0.5，通过mixup方法进行出清价格数据增强得到数据如图3所示，其中后360个数据为原始数据。

图3 数据增强后的出清价格数据

由引言对mixup方法的分析可知出清价格与时间的相关性会受到影响，这一点由图3可看出，但本文在特征选取时已将时段数据作为其中一项，因此可避免此类影响。

(3) 对出清价格进行HHT分析，得到各分量及其瞬时频率如图4、图5所示。

由图4～图5可知：IMF1～IMF3频率值较高，均值大于0.05。采用GradientBoostingRegressor算法；瞬时频率均值小于0.05的低频分量IMF4～IMF7和余项RESn采用神经网络算法。

图4 EMD分解结果

图5 各分量瞬时频率

为证明GradientBoostingRegressor算法的优越性，选择KNeighbordRegressor、ExtraTreesRegressor算法，对IMF1进行拟合，并预测未来24小时时段的出清价格高频分量，结果如图6所示。

图6 IMF1预测结果

采用平均绝对误差MAE、均方误差MSE对模型进行评价。值越小说明误差越小，预测效果越好[7]。对比结果如表1所示。

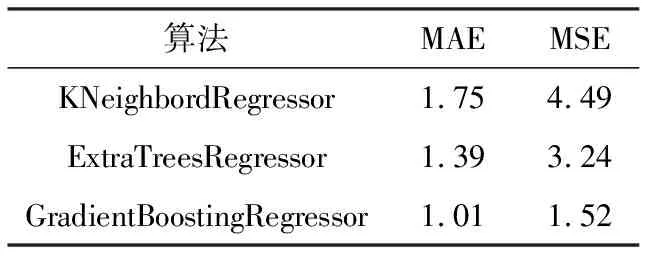
表1 预测对比

分析图6和表1，针对本文设置的特征项与预测目标项，GradientBoostingRegressor的预测效果相对较好。

(4) 训练模型并预测。为对比mixup与HHT融合的方法是否具有优越性，本文建立另外两类模型。

① 采用原始出清价格数据，使用GradientBoostingRegressor算法模型进行价格预测。

② 采用原始出清价格数据，但该模型将对数据进行HHT分解分析，并同本文前述方法针对高低频IMF分量进行单独预测并累加得到预测结果。

三种方法对未来24个时段出清价格预测得到的结果，如图7所示。

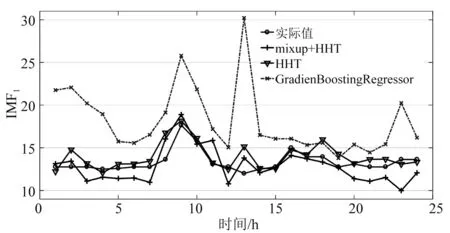
图7 出清价格预测结果

定义新指标回归预测平均准确率MA(mean accuracy)：

(10)

Ei=|y预测值-y实际值|/y实际值

(11)

对比结果见表2。

表2 电价预测对比

由表2可知，尽管经过HHT分解后的组合预测方法较单一模型相比已提升35.48%准确率，但采用mixup数据扩充和HHT分解后的模型与HHT方法相比，可进一步提升准确率1.89%。

4 结束语

本文提出的基于mixup和HHT的出清电价组合预测方法，可改善由于电力市场改革过程中交易系统运行数据量少、竞价规则计算方式引起的数据波动性增加和单一预测方法准确性低等对于预测结果的影响，从而提升预测准确率。