电动汽车电驱动系统机电耦合动态特性研究

葛帅帅，杨雨番，郭 栋，张志刚，易园园

（1.重庆理工大学 车辆工程学院，重庆 400054；2.江汉大学 智能制造学院，武汉 430056）

电驱动系统是电动汽车核心部件之一，其性能直接影响电动汽车的安全与可靠性。电驱动系统主要由电机和齿轮传动机构组成，是一个典型的机电耦合系统。当电动汽车在变速变载等典型工况下行驶时，会使得机电耦合系统的动力学特性更加复杂，甚至导致传动系统零部件发生故障失效。因此，考虑电驱动系统机电耦合效应，研究电驱动系统在典型工况下的动态特性，对于保证电动汽车运行安全性及可靠性具有重要理论意义。

近年来，电驱动系统机电耦合特性已成为国内外学者的研究热点。Bai等［1］考虑电机的磁场分布和传动系统的时变刚度，建立了机电耦合动力学模型，发现在电机电压和传动系统负载发生瞬变时会使机电耦合系统产生剧烈振动。Abraham G等［2］建立了永磁同步电机有限元仿真模型，研究了电极数量和定子槽对电机电磁转矩波动的影响。文献［3-4］基于Park变换和傅里叶变换，建立了混合动力汽车的永磁同步电机模型，研究了电机参数对机电耦合系统的影响。Ishikawa［5］忽略传动系统内部作用，建立了包括永磁同步电机模型及简化为惯性转子的传动系统模型，阐述了电动汽车机电耦合系统容易受到电机转速和传动系统负荷影响的特性。文献［6-8］忽略了传动系统齿轮啮合产生的非线性力，建立高速列车牵引-传动系统的机电耦合动力学模型，研究电机参数对机电耦合系统动力学特性的影响。以上研究主要集中在电机电磁作用下的电磁转矩脉动方面，很少考虑齿轮传动系统机械动力学特性。于蓬等［9-10］建立了包括电机的Park变换模型和传动系统柔体模型的电动汽车电驱动系统机电耦合动力学模型，研究了控制策略对机-电-磁多物理场耦合下的电驱动模型的影响，并分析了稳定转速下电机电磁刚度对系统振动特性的影响规律。张立军等［11］对某燃料电池轿车在加速启动和回馈制动的纵向振动问题进行了分析，考虑齿轮齿侧间隙和轮胎-地面的摩擦动力学，建立了电机-减速器模型，发现在电机转矩瞬间下降时，齿轮齿侧间隙的存在会导致齿轮拍击产生振动和噪声。文献［12-15］建立了包括截割电机和截割传动系统的采煤机截割系统动力学模型，研究了变速变载工况下，内外激励对机电耦合系统扭振的影响。

以上文献大多聚焦在采煤机截割系统、高速列车牵引系统及永磁同步电机等领域的机电耦合动力学分析，而在电动汽车电驱动系统机电耦合方面研究相对较少。部分文献虽建立了较为复杂的电动汽车电驱动系统机电耦合模型，但大多将依据经验或实验数据获得的电磁激励作为已知先验函数施加于电机转子，无法满足非稳态运行工况。

本文中以某电动汽车电驱动系统为研究对象，首先建立了包括两级减速器、永磁同步电机在内的齿轮传动系统扭转振动模型、基于d-q轴变换的永磁同步电机Park模型，在此基础上建立电驱动系统机电耦合动力学模型。仿真分析稳态工况、冲击载荷工况、起伏路面工况等3种工况下的电驱动系统机电耦合动态响应，揭示电驱动系统电机与齿轮传动系统的机电耦合关系，为进一步研究电动汽车电驱动系统主动减振控制策略提供参考。

1 电动汽车电驱动系统机电耦合动力学模型

图1为电动汽车电驱动系统结构示意图，主要结构包括永磁同步电机、齿轮传动系统等。

图1 某电动汽车电驱动系统结构示意图

1.1 永磁同步电机模型

齿轮传动系统由永磁同步电机驱动。采用Park变换，在d-p坐标轴下建立永磁同步电机的等效电路模型。对应的电机电压方程和电磁转矩方程为

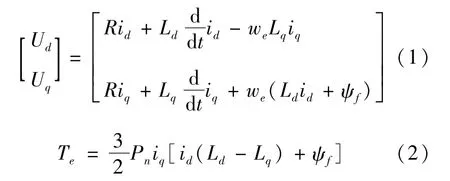
式中：Pn为电机极对数；Ud、Uq分别为d、q轴电压；id、iq分别为d、q轴电流；Ld、Lq分别为d、q轴电感参数；ψf为永磁体磁链参数；we为基波电压角速度；R为电机定子电阻；ψd、ψq分别为d、q轴上的永磁体磁链分量。

1.2 齿轮传动系统扭转振动动力学模型

1.2.1 齿轮副啮合力模型

忽略传动轴的横向和轴向变形，仅考虑齿轮的扭转振动，建立2自由度齿轮副扭转振动模型，如图2所示。

图2 齿轮副啮合模型示意图

计入啮合阻尼的齿轮动态法向啮合力可表示为：

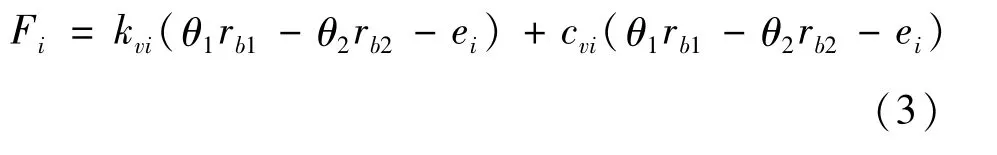
式中：i为参与啮合的齿轮序号，i=1，2；kvi、cki为齿轮对i在啮合点处的综合啮合刚度和阻尼系数。

主、从动齿轮的力矩平衡方程为：

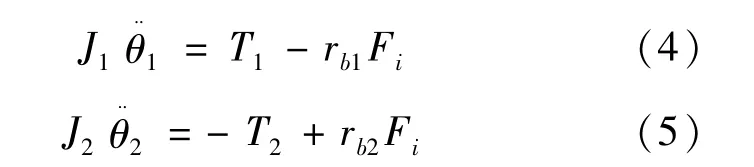
式中：θ1和θ2分别为主、从动齿轮的转角；J1、J2分别为两轮的转动惯量；T1、T2为驱动力矩和阻力矩；e1、e2为齿廓误差。用x表示齿轮动态传递误差，x=θ1rb1-θ2rb2-e（t），则间隙函数为：

式中：2b为齿轮副间隙；当f（x）=x-b时，轮齿处于正常啮合状态；当f（x）=0时，轮齿处于分离状态；当f（x）=x+b时，啮合轮齿处于齿背啮合状态。

1.2.2 齿轮系统扭转振动动力学模型

图3、4所示分别为齿轮传动系统模型和齿轮传动系统扭转振动动力学模型。综合考虑齿轮传动系统的刚体转动和弹性扭振，建立传动系统各构件的动力学方程，如式（7）所示。

图4中，JM、JL、J1、J2分别为电机、负载和主、从动轮的转动惯量；θ、θL、θ1、θ2分别为电机、负载和主从动齿轮的转角；k1、k2分别为主从动轴的扭转刚度系数；c1、c2分别为主从动轴的扭转阻尼系数。

图3 齿轮传动系统模型示意图

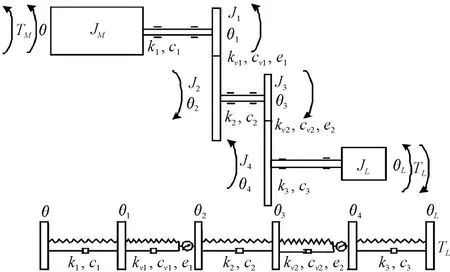
图4 齿轮传动系统扭转振动动力学模型示意图

考虑电机的特性，即计入电机的速度波动，取θ、θL、θ1、θ2为系统的广义坐标，用牛顿-欧拉方法建立系统的动力学方程为：

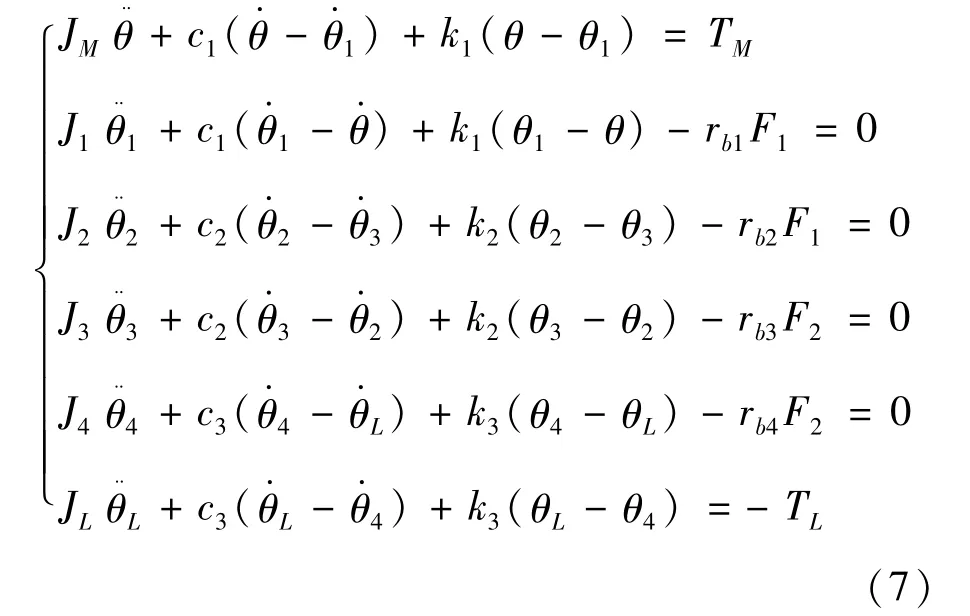
式中：rb1、rb2、rb3、rb4分别为4个齿轮的基圆半径；F1、F2分别为第1对和第2对轮齿间的动态啮合力：

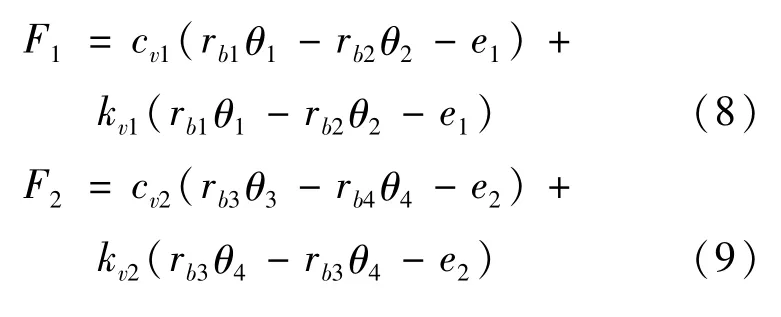
式中：TM、TL分别为驱动力矩和负载力矩；cv1、cv2分别为齿轮啮合阻尼系数；kv1、kv2分别为齿轮啮合刚度系数。将TM、TL的变化规律代入式（7），求出电机的角度变化规律，即速度波动。

1.3 电动汽车电驱动系统机电耦合模型

电机通过磁场将电源的电能转换为转子的机械能，转子直接和传动系统相连，因此通过建立电机输出转矩等于传动系统输入转矩的等式可将电气系统和机械系统联合到一起，从而得到电动汽车电驱动系统机电耦合模型，见图5。

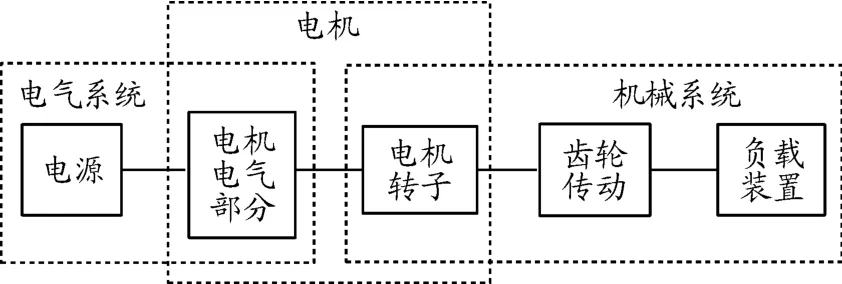
图5 电动汽车电驱动系统机电耦合模型框图

2 电动汽车电驱动系统机电耦合动态特性分析

以某电动汽车的电机和减速器为例进行研究，搭建某电动汽车电驱动系统机电耦合仿真模型。电驱动系统主要仿真参数如表1所示。

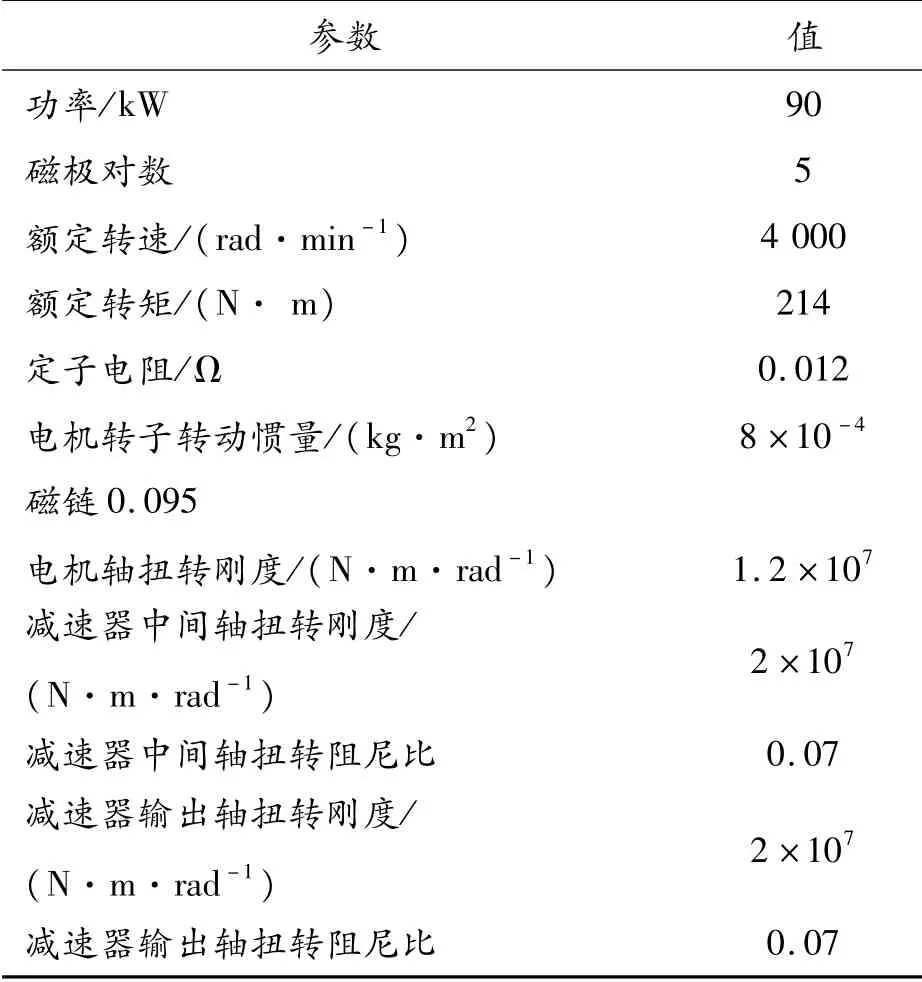
表1 电驱动系统主要仿真参数

2.1 稳态工况下对电驱动系统机电耦合动态特性的影响

为研究稳态工况下对系统的影响，对机电耦合系统施加恒转速、恒负载工况分析齿轮传动系统的动态响应和电气系统的电信号动态响应。

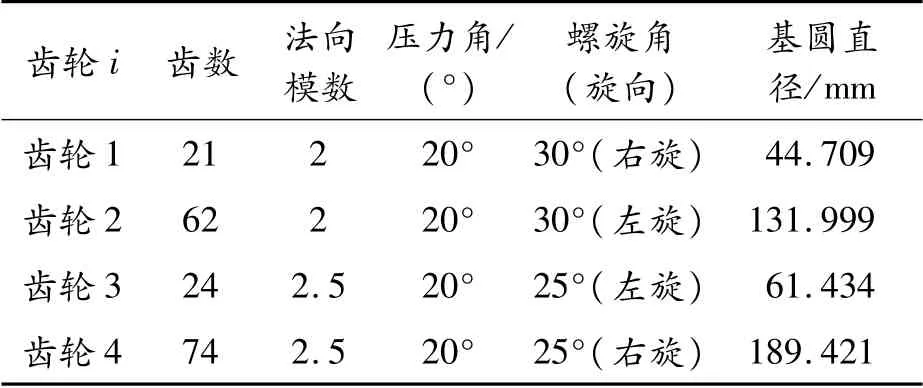
表2 齿轮传动系统基本参数

图6所示为电机转速为4 000 rad/min时的传动系统动态啮合力响应图。fmg（g=1，2）表示从电机到负载端的各级齿轮副啮频，fst（t=1，2，3）表示传动轴转频（fm1=1 400 Hz，fm2=541.92 Hz，fs1=66.67 Hz，fs2=22.58 Hz，fs3=7.32 Hz）。传动系统的啮合力频谱图中含有2对齿轮副的啮频信息，但主导频率还是第1对齿轮副的啮合频率及其倍频。

电机转速频率中含有机械传动系统的啮合频率及其倍频（见图7），表明电机转速会受到齿轮啮合力频率的影响，降低电机转速中啮合力频率的含量将会减小电机转速波动。

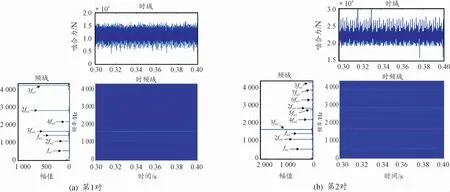
图6 电机负载214 N·m齿轮啮合力动态响应

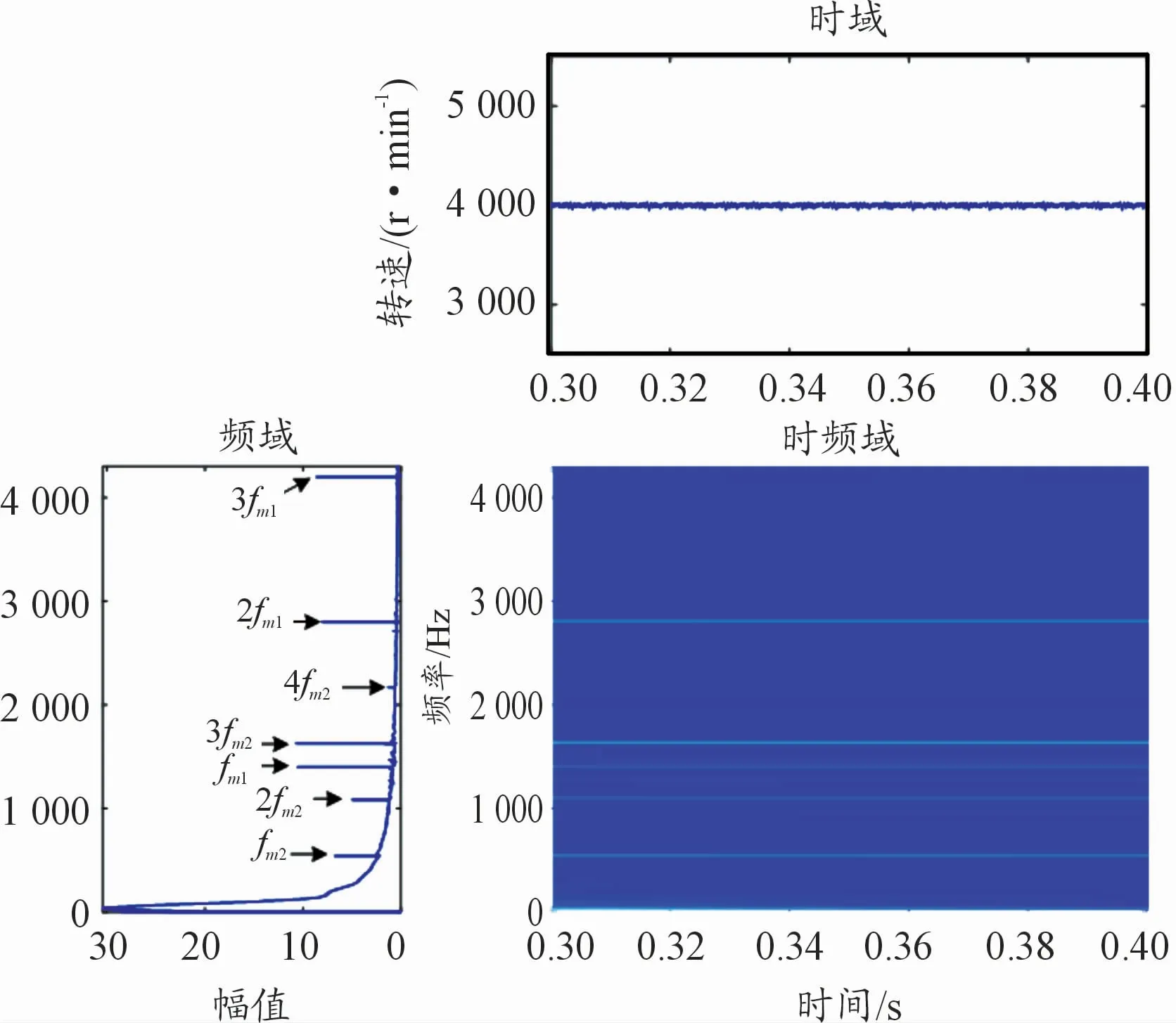
图7 电机负载214 N·m电机转速动态响应

图8 为电流频谱图，其中含有丰富的传动系统频率信息，包括各级转频、啮频及其倍频，但幅值较小。机械系统的频率对电气系统中的定子电流进行调制，表明电气系统会受机械系统影响。

2.2 冲击载荷对电驱动系统机电耦合动态特性的影响

为研究电驱动系统在冲击载荷下的动态响应特性，对系统施加冲击载荷进行仿真，并对机电耦合系统的动态响应进行分析。

对电机轴施加1个冲击载荷（如图9），在0.2 s时从0.5Tn阶跃至1Tn（Tn为电机额定负载转矩）。

图8 电机负载214 N·m电机定子电流动态响应

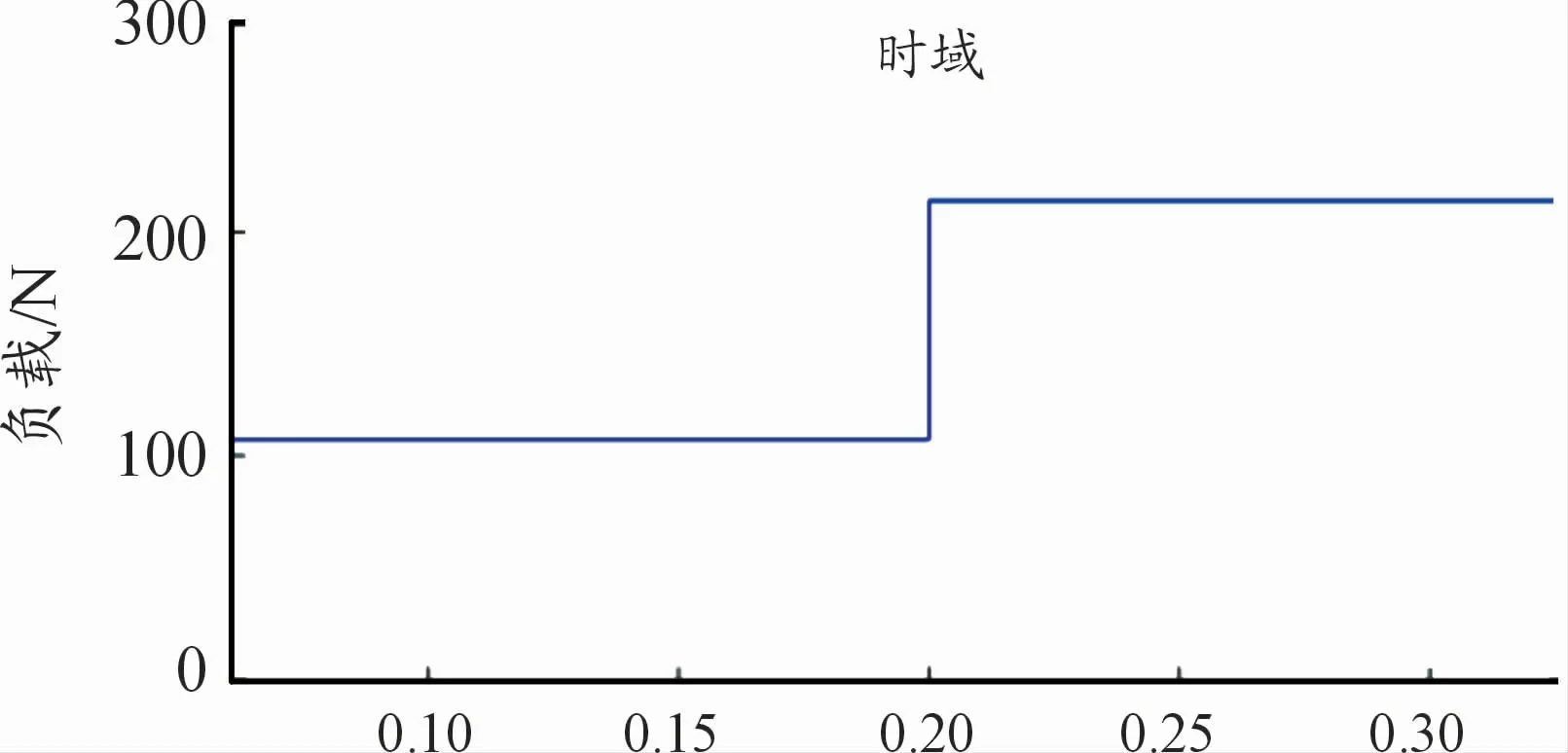
图9 电机轴冲击载荷

图10 、11分别为电机轴动态转速响应和齿轮动态啮合力响应。

图10 冲击载荷下电机转速动态响应

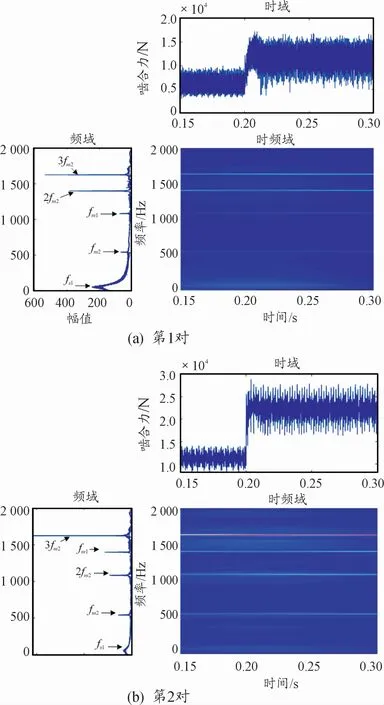
图11 冲击载荷下齿轮啮合力动态响应

在0.2 s时负载突变，电驱动机电耦合系统受到冲击后，传动系统啮合力、电机轴转速、定子电流的相应频率及其倍频的幅值都会瞬间增大。特别是电机轴转频幅值和齿轮啮频幅值变化明显，更容易因扭振而产生传动轴的断裂，导致齿轮的损坏对电动汽车的安全性造成威胁。设计传动系统时应考虑该问题。

图12为负载突变过程中电机定子动态电流响应。在频域图中，定子电流频率包含电流频率和微弱的齿轮啮频及轴转频，且电流频率受到传动系统频率的调制。当负载发生突变时，电流频率会发生突变，表明电气系统会受到传动系统瞬态振动的影响。

图12 冲击载荷下电机定子电流动态响应曲线图

2.3 正弦波动载荷对电驱动系统机电耦合动态特性的影响

电动汽车行驶时常会面临各种路况。稳态工况和冲击载荷工况仅是车辆行驶工况下的一部分，还有在起伏路面行驶的工况。因此仅对稳态和突变载荷工况进行仿真分析不足以表明典型工况下电动汽车的机电耦合系统响应特性。于是采用正弦函数（频率为7 Hz）来模拟起伏路面工况下的负载（如图13），研究起伏路面下电动汽车电驱动系统的机电耦合动态特性。

图13 系统负载转矩曲线图

如图14～16所示，随着负载呈正弦波变化，电机输出转速、齿轮啮合力、电机定子电流整体上也呈现正弦变化；和冲击工况下幅值明显增长相比，该工况对啮合力频率幅值影响不大，表明在负载变化缓慢的工况下，有利于减小电动汽车电驱动系统的扭转振动，延长零部件使用寿命。

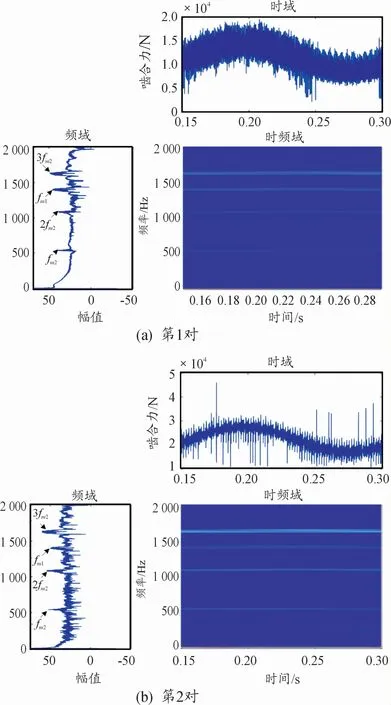
图15 正弦波动载荷下齿轮啮合力动态响应曲线图

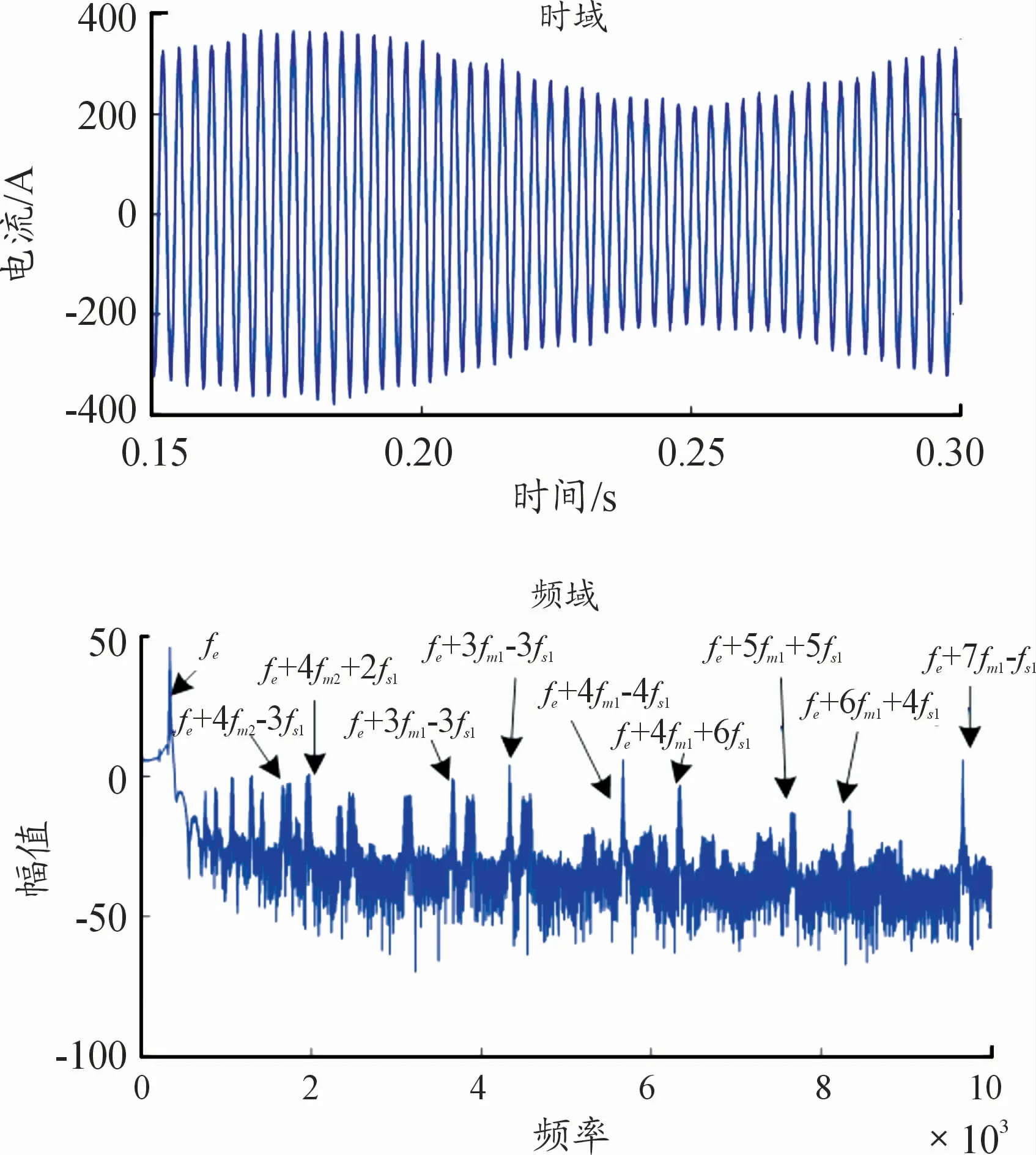
图16 正弦波动载荷下电机定子电流动态响应曲线图

电流信号中含有的机电耦合信息比转速及啮合力更加丰富，因此可用电流来监测典型工况下机电耦合系统运行状态，与分析相符。综合3种工况下的电流频谱图来看，负载突变工况下的电流频谱图包含的传动系统频率信息最明显，即该工况下定子电流信号监测传动系振动状态的效果最好。

3 结论

1）电机转速频谱中含有齿轮传动系统的各级齿轮啮频。定子电流被传动系统的啮频和转频调制，使得电机定子电流中含有丰富的传动系统频率信息。表明电驱动系统的电气系统受机械传动系统扭振影响；电机与传动系统之间存在明显的机电耦合效应。

2）与电机转速相比，由于电机定子电流信号含有更加丰富的齿轮传动系统频率信息，因此可通过分析电机定子电流频率信号来监测齿轮传动系统啮合振动状态，特别是在负载突变工况下，电流频谱图包含传动系统频率信息最明显，即该工况下定子电流信号监测传动系振动状态的效果最好。