基于神经元PID控制的四开关三相Buck-Boost逆变器研究

成蒙，肖伸平，岳舟

(1.湖南工业大学 电气与信息工程学院，湖南 株洲，412007；2.湖南人文科技学院 能源与机电工程学院，湖南 娄底，417000)

双级逆变器通常利用其中1个变换器(Boost，Buck-Boost，Cuk，Speic或Zeta)来提高一级逆变器的直流输入电压，再利用六开关三相(six switches three-phase，SSTP)逆变器来实现二级逆变器的DC-AC变换，此外，还能够匹配大范围的输入电压，可用于各种工业应用，如UPS、各类可再生能源系统、电机驱动和有源电力滤波器等。但复杂的结构使其成本高昂，而且体积更大[1]。单级逆变器通过对直流输入电源进行降压/升压变换，同时提供交流输出电源[2]。也有学者研究并设计了四开关三相(four switches three-phase，FSTP)逆变器[3]。图1所示为传统的FSTP逆变器拓扑结构，这种拓扑结构已在很多场合中得到应用，其中，两相负载由2个桥臂逆变器提供支持，第三相负载由施加在直流电源上的2个电容(C1和C2)的中点供电。

图1 FSTP电压源逆变器拓扑结构Fig.1 Topology of FSTP Voltage Source Inverter

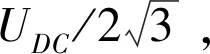
基于以上问题，本文提出一种基于Buck-Boost的FSTP逆变器拓扑结构，叫做FSTP Buck-Boost逆变器。其结构简单，控制方便，且具有反相输出电压升降能力，被广泛应用于降压或升压DC-DC开关电路、光伏最大功率点跟踪[10]和功率因数校正电路[11]。基于上述优点，Buck-Boost变换器近年来在各种拓扑结构中得到了学者们的广泛研究[12-13]。

在每个Buck-Boost变换器中，采用不同的控制策略控制变换器的性能，从而产生通过电容的输出正弦电压，每种控制方法都有其优缺点。文献[14]中的PID控制策略通常用于DC-DC变换器双环控制，第1个回路称为内环，通过减小参考电流和测量电流之间的误差来控制通过电感的电流。第2个回路称为外环，由电容上的参考电压和期望输出正弦电压之间的误差组成。虽然PID控制结构简单、调整方便且稳定性好，但在整定参数时，方法较为繁杂，各个控制器的参数整定通常不够理想，尤其是在被控对象具有时变以及非线性特性时，PID控制方法的适应性较差。文献[15]将滑模控制应用于FSTP Buck-Boost逆变器，滑模控制与PID控制相比，其抗干扰能力较强，但滑模控制输出电压的超调较大，响应速度较慢。另外，在文献[15]的仿真波形中，横轴(即时间轴)的时间起点都是从0.04 s开始，无法反映系统初始状态的性能。

为解决上述控制策略存在的问题，引入广泛适用于非线性系统控制的神经元PID控制方法[16]。由于神经元具有自学习及自适应能力，因此，在控制过程中不依赖被控对象的数学模型，其动态和稳态性能良好，且鲁棒性较强。负载发生突变时，在神经元PID控制器的调节作用下，系统能较好地抑制扰动。所提出的FSTP Buck-Boost逆变器虽然没有升压能力，但其输出电压比传统的FSTP逆变器高2倍，从而提高了输入直流电源的电压利用率。该逆变器的另一个显著优点是其输出电压为纯正弦波，降低了输出级的滤波要求。此外，不需要在同一桥臂开关之间插入死区，明显降低了输出波形失真和增益非线性。因此，该新型逆变器具有比较重要的研究意义和实用价值。

1 FSTP Buck-Boost逆变器拓扑结构

所提FSTP Buck-Boost逆变器新拓扑结构由2个双向Buck-Boost变换器组成，通过在2个Buck-Boost变换器的输出端附加两相负载，得到如图2所示的DC/AC变换，最后一相负载连接到直流电源的负半输入端。2个Buck-Boost变换器都能提供负直流偏置正弦波输出。这种偏压恰好就是带有负符号的输入电源电压。最后，由于负载通过2个变换器和直流输入电源进行差动连接，因此，任何两相负载上的直流偏压被彼此抵消。通过抵消负直流偏压后，负载上产生的电压为正弦电压，而且通过负载产生的电流波形也是正弦波。

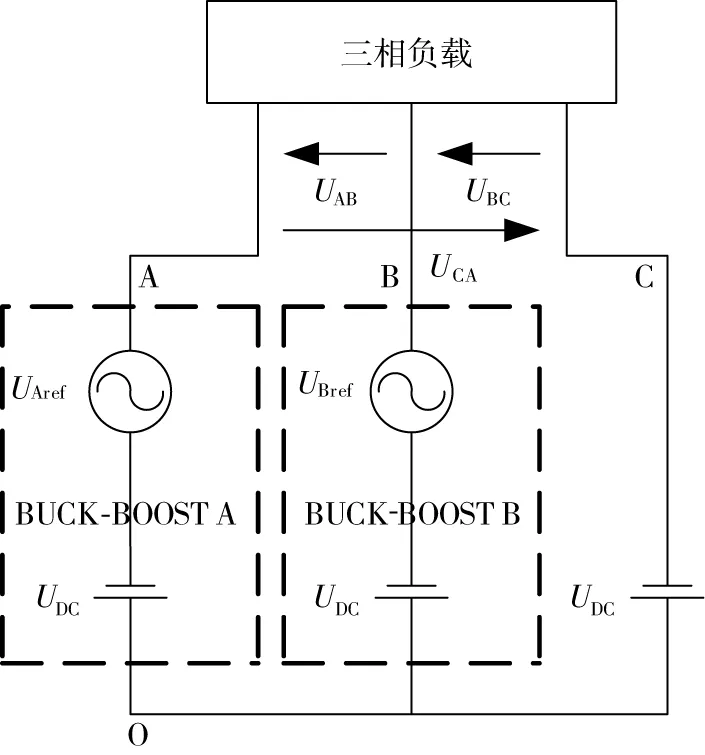
图2 使用2个Buck-Boost变换器进行DC-DC转换的参考结构Fig.2 A reference construction for DC-AC conversion with double Buck-Boost Inverters

图3所示为Buck-Boost变换器电路的拓扑结构，它的输出电压可能小于也可能大于带负号的输入电压。

图3 Buck-Boost变换器的结构Fig.3 Topology of Buck-Boost Inverter

输出和输入电压的方程式如下所示：

(1)

其中：D为占空比；Uin为输入电压，Uin等于图4所示拓扑结构中的UDC；Uo为输出电压。每个Buck-Boost变换器的调制波分别为式(2)中带直流偏置的正弦信号UAO和UBO：

(2)

其中：UAO和UBO为2个Buck-Boost变换器的参考电压；UAref和UBref分别为A相和B相的正弦参考电压，都加上-UDC之后，即构成了带负直流偏置的参考电压UAO和UBO；UmL-L为期望输出线电压的幅值；ω为输出电压频率。通过负载获得的线电压如下：

(3)

综合图2和图3得到新型FSTP Buck-Boost逆变器的电路拓扑结构，见图4。该新型拓扑结构可以产生与输入电源电压近似相等的幅值电压，但需要使UmL-L小于直流偏置电压，以避免出现故障占空比，即占空比超出0～1的范围。

图4 所提FSTP Buck-Boost逆变器的拓扑结构Fig.4 Proposed topology of FSTP Buck-Boost Inverter

与FSTP Sepic和Zeta逆变器[6,8]相比较，本文所提FSTP Buck-Boost逆变器的元件数量减少，而且在闭环控制系统的测量中，每个变换器中只有1个电感和1个电容，需要的传感器硬件元件较少。此外，FSTP Buck-Boost逆变器因为使用较少的磁性元件，减小了装置的尺寸、质量、导通损耗以及节约了系统成本，因此，该新型拓扑具有广阔的应用前景。

2 神经元PID控制

神经元PID由单神经元和常规PID结合而成[16]。单神经元具有自学习及自适应能力，再结合常规PID的优点构成了应用于FSTP Buck-Boost逆变器的神经元PID控制方法，其控制算式如下：

Δu(k)=w1[e(k)-e(k-1)]+w2e(k)+w3[e(k)-2e(k-1)+e(k-2)]

(4)

图5所示为神经元PID控制原理框图。图5中，r为设定值；y为实际输出；e为系统误差。转换器的输入反映的是被控过程与控制设定的状态，通过转换器将系统误差转换成状态变量x1，x2和x3。这里x1(k)=e(k)，x2(k)=Δe(k)，x3(k)=e(k)-2e(k-1)+e(k-2)，wi(k)为对应与xi(k)的加权系数，K为神经元的比例系数，也叫作增益，且K>0。神经元的控制信号由关联搜索产生，即

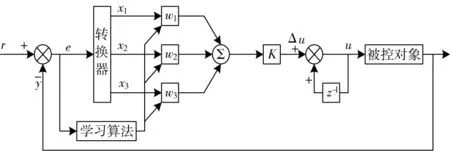
图5 神经元PID控制原理框图Fig.5 Schematic diagram of neuron PID control

(5)

通过调整加权系数以实现神经元PID控制器的自适应及自组织功能，而加权系数是利用有监督的Hebb学习规则来进行调整，且加权系数与神经元的输入、输出及输出偏差的函数有关，即：

wi(k+1)=(1-c)wi(k)+ηri(k)

(6)

ri(k)=e(k)u(k)xi(k)

(7)

式中：ri(k)为递进信号，且逐渐衰减；e(k)为系统误差；η为学习速率，且η>0；c为常数且c≥0。

将式(7)代入式(6)有

(8)

其中：Δwi(k)=wi(k+1)-wi(k)。

如果存在函数fi(wi(k),e(k),u(k),xi(k))，有

(9)

则式(8)变换为

(10)

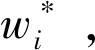
为保证式(6)和式(10)的收敛性及鲁棒性，规范化处理上述学习算法可得：

(11)

PID系数分别采用不同的学习速率，根据需要进行调整各自的权系数，其取值由仿真与实验确定，这里取c=0。

神经元PID参数的在线学习主要与e(k)和Δe(k)有关[17]。因此，可以通过修改加权系数学习修正部分，即将其中的xi(k)改为e(k)+Δe(k)，其算法如下：

(12)

通过改进算法，权系数的在线修正可根据实际经验制定，而不再是完全根据神经网络学习原理得到。其参数调整的规则如下：

1)对于没有超调且上升时间长的阶跃输入，则增大K，保持ηp，ηi和ηd不变；若输出较大的超调，甚至出现震荡，则减小K，保持ηp，ηi和ηd不变。

2)对于系统响应产生多次正弦衰减的阶跃输入，则应减少ηp，保持另外几个参数不变。

3)若系统响应上升时间长，增大ηi出现较大的超调，则应适当增加ηp，保持另外几个参数不变。

4)若系统响应上升时间短，且有较大的超调，则减少ηi，保持另外几个参数不变。

5)在调整初始阶段，ηd应选择较小值，当调节ηi，ηp和K使系统响应具有良好特性时，再逐渐增加ηd，而保持另外几个参数不变，使系统稳态输出基本无纹波。

3 仿真对比与分析

分别采用滑模控制和神经元PID控制，对所设计的FSTP Buck-Boost逆变器在稳态和动态工作条件下进行对比仿真研究，系统的参数设置见表1。图6和图7所示分别为采用滑模控制的稳态与动态仿真结果，图8和图9所示分别为采用神经元PID控制的稳态和动态仿真结果。

表1 FSTP Buck-Boost逆变器的参数Table 1 Specifications FSTP Buck-Boost inverter

图6所示为采用滑模控制时逆变器的稳态性能，其中，图6(a)所示为输出相电压仿真波形，图6(b)所示为输出电流仿真波形。

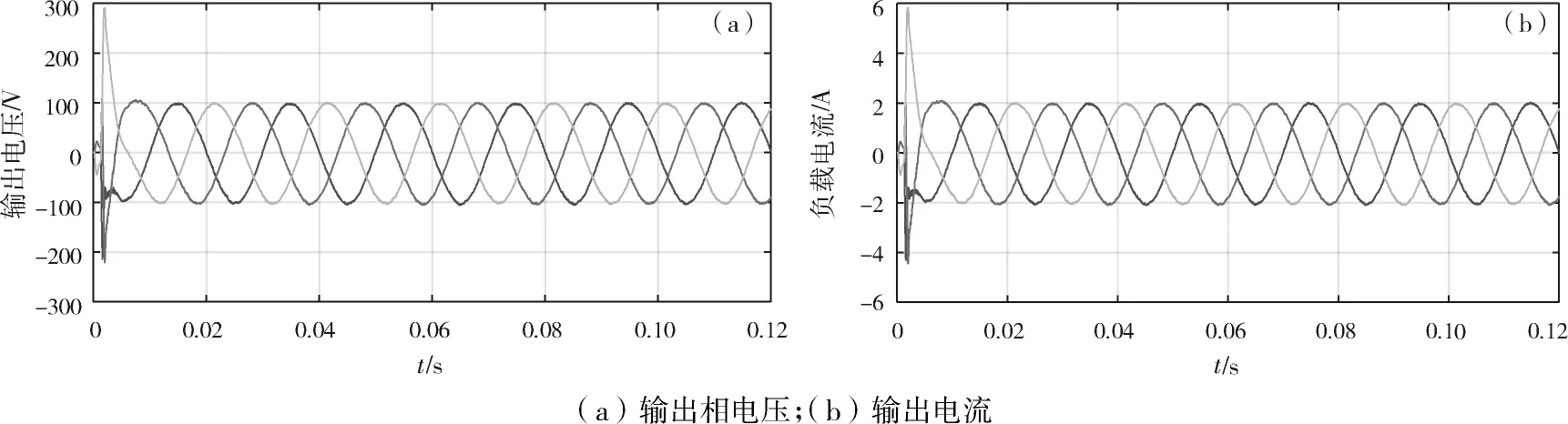
图6 采用滑模控制的稳态性能Fig.6 Steady-state performance with sliding mode control

图7所示为采用滑模控制时逆变器的动态性能，其中，图7(a)和图7(b)所示为负载从50 Ω突变至100 Ω的仿真结果，图7(c)和7(d)所示为负载从100 Ω突变至50 Ω的仿真结果。

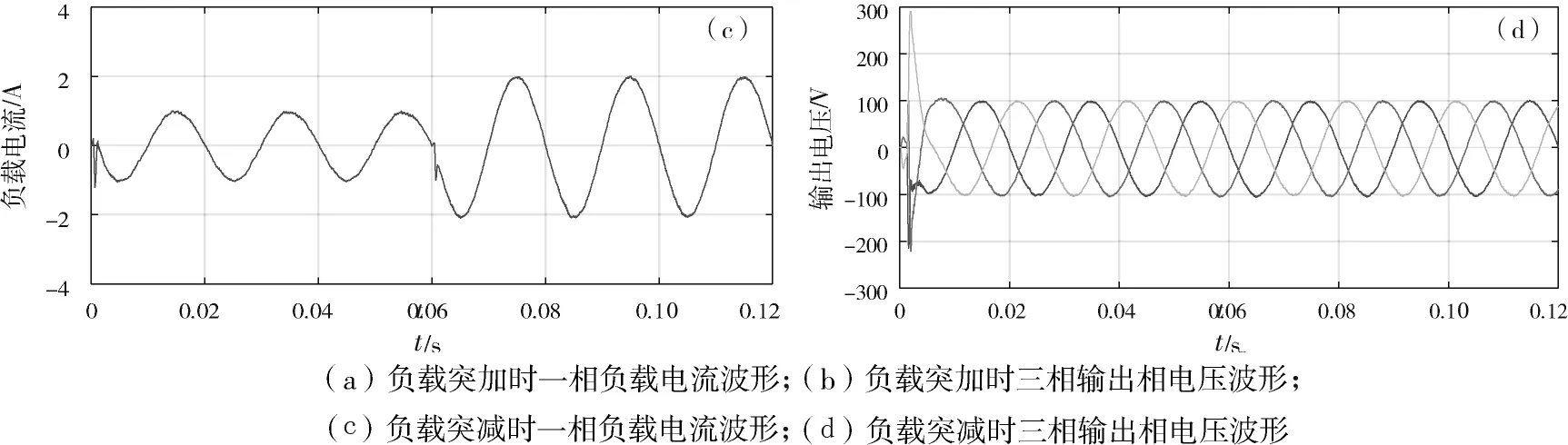
图7 采用滑模控制的动态性能Fig.7 Dynamic performance with sliding mode control

图8描述了采用神经元PID控制时逆变器的稳态运行。图8(a)是输出相电压仿真波形，图8(b)是输出电流仿真波形。

图8 采用神经元PID控制的稳态性能Fig.8 Steady-state performance with neuron PID control

图9所示为采用神经元PID控制时逆变器的动态性能，其中，图 9(a)和9(b)所示为负载从50 Ω突变至100 Ω的仿真结果，图 9(c)和9(d)所示为负载从100 Ω突变至50 Ω的仿真结果。从仿真结果可以看出，系统能够快速达到稳态，具有良好的动态响应能力。

图9 采用神经元PID控制的动态性能Fig.9 Dynamic performance with neuron PID control

表2所示为小波分析包抽取的数据及其计算结果。对比图6和图8，并从表2可以看出：由于积分项的存在，当初始误差较大时，滑模控制会导致饱和，使输出电压的超调量达到了191.22%，且到达稳态的时间更长、效果更差。神经元PID控制消除了初始误差，使系统在初始时刻便迅速达到稳态，所以，输出电压超调很小仅有0.52%，到达稳态值的时间短，且神经元PID控制具有较强的跟踪能力。对比图7和9可以看出：在负载发生突变的情况下，这2种控制方法下的电压波动都很小，且都能很快恢复至稳定状态，说明这2种控制方法都具有较强的抗扰动能力。由仿真结果可以看出，神经元PID控制方法既能够使系统输出保持很小的超调量，又能够保持较强的抗扰动能力。

表2 电压超调数据Table 2 Voltage overshoot data

4 样机试验

为了进一步验证FSTP Buck-Boost逆变器其拓扑结构的正确性和控制策略的可行性，将TI公司的TMS320F2812处理器作为控制核心、IGBT作为功率开关器件制作了试验装置。图10所示为样机试验装置，其中图10(a)所示为试验装置主电路FSTP Buck-Boost逆变器，图10(b)所示为试验装置控制电路数字信号处理器TMS320F2812。图11所示为稳态情况下FSTP Buck-Boost逆变器输出相电压和输出电流的试验波形。图11(a)所示为输出相电压波形，图11(b)所示为输出电流波形。负载突变的试验结果见图12，图12(a)所示为负载从50 Ω突增至100 Ω时的情形，图12(b)所示为负载从100 Ω突减至50 Ω时的情形，示波器波形从上到下分别是一相负载电流波形与三相输出相电压波形。由试验结果可以看出，系统能在较短时间内恢复稳定，且具有良好的动态性能。

图10 样机试验装置Fig.10 Test devices of prototype

图11 输出电压电流试验波形Fig.11 The experimental waveform of output voltage and current

图12 负载突变试验结果Fig.12 The test results of load mutation

试验结果表明，输出电压和电流的波形自然正弦(不需要滤波器)，并具有较好的质量，试验波形和仿真波形大体相同，于是更加验证了本文所提的FSTP Buck-Boost逆变器其拓扑结构的正确性和控制方法的可行性。

5 结论

本文提出的FSTP Buck-Boost逆变器拓扑结构与已有的FSTP Sepic/Zeta逆变器相比，具有硬件元件少、传感器少、体积小、成本低和控制复杂度低等优点。FSTP Buck-Boost逆变器相比与传统的四开关或六开关逆变器相比，实现了一级DC/AC能量转换，可以在不需要滤波器的情况下产生正弦输出电压。对比滑模控制，本文采用的神经元PID控制能够消除初始误差，使系统初始时刻便达到稳态值，因此，输出电压超调很小，到达稳态值时间短，且能够以高效率的方式对参考电压进行跟踪。仿真研究与样机试验验证了拓扑结构的正确性以及控制策略的可行性。