多元线性回归方法在地面沉降量预测中的解析及应用

王 琰，吕 航，谷复光*

(1.吉林建筑大学测绘与勘查工程学院，吉林 长春 130118；2.吉林大学新能源与环境学院，吉林 长春 130021)

随着工业发展和城市化进程的逐步推进，地面沉降在全世界范围内普遍发生，引发了建筑物开裂破坏、城市内涝、防潮抗洪能力降低等各种灾害。经过众多学者多年来的监测、分析与模拟研究，认为地下水开采是引发大面积地面沉降的主要原因，特别是在第四纪松散沉积层分布的地区，由地下水水位急剧、广泛下降引起的地面沉降问题日趋严重。如何基于描述地下水流场的变化，确立准确、高效的地面沉降计算和预测方法，对于控制地面沉降的发展至关重要。

国内外许多学者基于各地区水文地质条件以及地下水水位和地面沉降量的动态监测结果，提出了一些地下水开采引起地面沉降的预测方法，主要包括数值计算法和数理统计法两大类。数值计算法主要有两步计算模型(如Gambolati等最早提出两步计算模型)、部分耦合模型(如Fokker等在两步计算模型的基础上，结合地下水流方程和Terzaghi固结理论，建立了模拟多层含水层系统的地下水流和总沉降量的数学模型)、考虑三维渗流与一维固结模型(如薛禹群等建立了三维变系数渗流模型和垂向一维沉降模型，分析了长江三角洲南部区域的地面沉降问题)和三维渗流与三维固结完全耦合模型(如Luo等、徐成华等在黏弹塑性比奥固结理论的基础上建立的地下水开采与地面沉降全耦合模型)，该方法相对来讲具有计算复杂、占用计算空间大、耗时多、许多参数难以确定等缺陷，采用数值计算方法进行地面沉降量的计算和预测时需花费大量的时间和人力进行模型建立和参数识别，计算速度相对较慢。相对于数值计算法，数理统计法在统计资料完整的情况下，拥有计算速度快、应用性较强等优势。

本文在分析地下水渗流与地面沉降间相关原理的基础上，采用数理统计方法，依据工程实例分析了地面沉降量与地下水水位变化之间的相关关系，建立了两者之间的多元线性回归模型，用来预测由地下水开采引起的地面沉降量的发展变化趋势，并通过对预测模型的检验，证明了该方法在地面沉降预测方面具有一定的可靠性和实用性。

1 地面沉降机理研究

1.1 地面沉降机理概化

天然土体是由矿物颗粒骨架、孔隙水和气体构成的固、气、液三相体系。根据有效应力原理，在含水介质骨架压缩的初始时段，土体中某一截面的上部荷载由有效应力(作用在矿物颗粒骨架上的应力)和孔隙水压力共同承担；随着地下水的持续开采，土体中地下水水位逐渐下降，孔隙水压力逐渐降低，作用在颗粒骨架上的有效应力随之增加；由于有效应力逐渐增加，土体骨架发生变化，从而导致土体体积改变，土体产生压缩变形。宏观上，各层土体压缩变形积累在地面即表现为地面沉降。

依据上述理论，分析并建立地下水开采过程中地下水水位变化值与土体变形量之间的关系，即可得到含水层的土体变形方程。

1.2 含水层可压缩土体一维变形关系

根据太沙基有效应力原理，考虑土体变形过程中侧向受限，土体变形主要产生在垂直方向上，且一段时间内土体承受的总应力不随时间变化等假设条件，有如下计算公式：

σ

′

=σ

-

u

(1)

式中

:σ

′为含水层土体承受的有效应力(MPa)

;σ

为含水层土体承受的总应力(MPa)；μ为含水层土体承受的孔隙水压力(MPa)

,

Δ

u=ρ

g

Δ

H[

其中

ρ

为水的密度

(

kg/m

)

，

g

为重力加速度

(

m/s

);

Δ

H

为孔隙水头变化值

(

m

)]

。

无压含水层系统中，含水层土体承受的有效应力的变化可表示如下：

(2)

土体中某一截面上，含水层土体承受的有效应力的变化可表示如下：

Δ

σ

′

=

-

ρ

g

Δ

H

(3)

由于土体有效应力的变化会导致土体骨架发生压缩，因此土体压缩系数

α

可表示为

(4)

式中

:V

为所取单元体积

(

m

);σ

′为含水层土体承受的有效应力(MPa)。

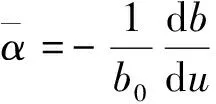
(5)

式中：

b

为可压缩含水层的初始厚度

(

m

)

；

b

为含水层厚度

(

m

)

。

根据一维太沙基有效应力原理，将公式(5)代入公式(2)、(3)中，可得：

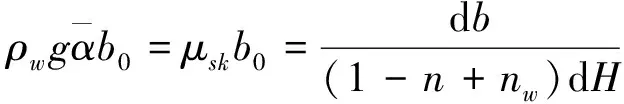
(6)

(7)

式中

:μ

为含水层土体的骨架储水率

(

1/m

)

，它是土体物理参数的函数。

因此，公式(6)、(7)可表示如下：

Δ

b=

-Δ

H(

1-

n

+

n

)μ

b

(8)

Δ

b=

-Δ

Hμ

b

(9)

式中

:

Δ

b

为含水层弹性压缩量与非弹压缩量

(

m

)

，正为压缩，负为扩张。

公式(8)、(9)即为计算潜水含水层(潜水含水层或因抽水含水层由饱和状态转为非饱和状态)土体垂向变形与承压含水层土体垂向变形的基本公式。对应土体变形的不同阶段，含水层土体骨架储水率的变化分别如下：

(10)

1.3 含水层土体压缩量计算

根据公式(8)、(9)，由地下水水位下降引起的含水层土体压缩量的计算模型如下18：

潜水含水层的弹性变形量为

Δ

b=

-Δ

H(

1-

n

+

n

)μ

b

=

-Δ

Hμ

(11)

潜水含水层的非弹性变形量为

Δ

b

=

-Δ

H(

1-

n

+

n

)μ

b

=

-Δ

Hμ

(12)

承压含水层的弹性变形量为

Δ

b=

-Δ

Hμ

b

=

-Δ

Hμ

(13)

承压含水层的非弹性变形量为

Δ

b

=

-Δ

Hμ

b

=

-Δ

Hμ

(14)

式中

:μ

为含水层土体骨架成分的弹性储水因子

(

无量纲

)

；

μ

为含水层土体骨架成分的非弹性储水因子

(

无量纲

)

；其他符号意义同上。实际地下水开发利用中，上述建立的含水层土体压缩量计算模型将被推广至各黏性土弱透水层，含水层及包含在其中的弱含水层被视为一个整体，整个土体骨架都可发生压缩，参数

μ

、

μ

是在整个土层规模上的等效参数。

2 地面沉降发展与地下水水位变化的相关性分析

2.1 场地概况

本研究选择的地面沉降多层位监测场地位于浙江省东部、长江三角洲东南角,平原区第四系厚度为50～110 m，最厚达120余米。监测目的地层由下至上分别为第四系上更新统下组砾石和中细砂组成的第Ⅰ承压含水层、上更新统上组下部细砂和含砾砂组成的第Ⅰ承压含水层、上更新统上组中部亚黏土组成的第Ⅱ黏性土弱含水层、全新统下组亚砂土构成的浅部孔隙承压含水层、全新统中组淤泥或淤泥质亚黏土构成的第Ⅰ黏性土弱含水层和全新统上组亚砂土构成的潜水含水层。场地所在区域自1982年开始少量开发地下水，开采量逐年增加，由于大规模开采地下水引起了较严重的地面沉降问题，为了保护环境，自2008年开始当地对地下水禁采，目前只预留少部分地下水井应急使用。

2.2 地面沉降发展与地下水水位变化的对比分析

根据地面沉降机理，地面沉降与地下水水位的变化存在密切的联系，故本文对研究场地内地面沉降及地下水水位监测点1985—2008年各含水层压缩沉降量与相应的地下水水位变幅数据进行了整理与分析，详见图1至图6。

图1 潜水含水层沉降逐年变化量与地下水水位逐年 变化量对比Fig.1 Comparison of annual variation of land subsidence and groundwater level of phreatic aquifer

图2 第Ⅰ黏性土弱含水层沉降逐年变化量与地下水 水位逐年变化量对比Fig.2 Comparison of annual variation of land subsidence and groundwater level of the first aquitard

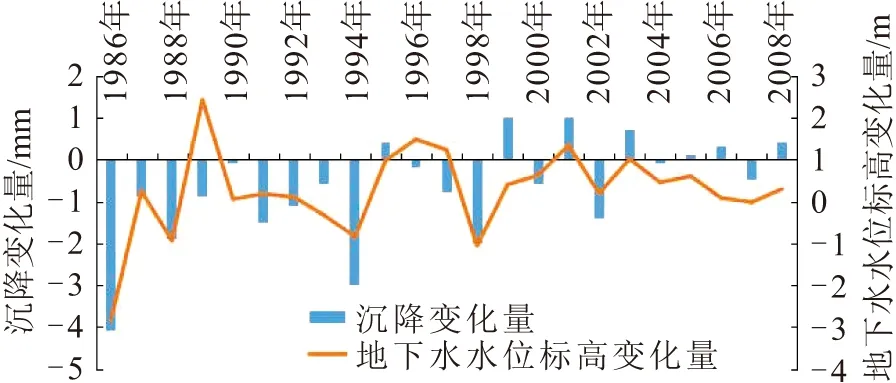
图3 浅部孔隙承压含水层沉降逐年变化量与地下水 水位逐年变化量对比Fig.3 Comparison of annual variation of land subsidence and groundwater level of shallow confined aquifer

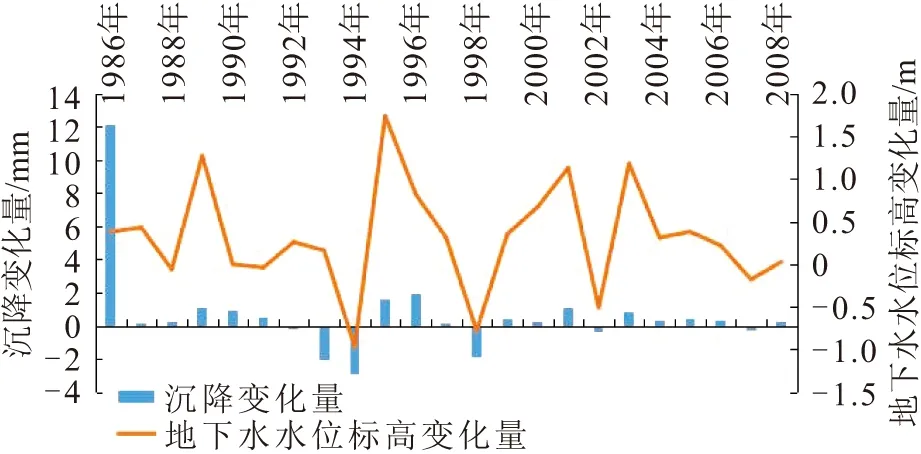
图4 第Ⅱ黏性土弱含水层沉降逐年变化量与地下水 水位逐年变化量对比Fig.4 Comparison of annual variation of land subsidence and groundwater level of the second aquitard

图5 第Ⅰ1承压含水层沉降逐年变化量与地下水 水位逐年变化量对比Fig.5 Comparison of annual variation of land subsidence and groundwater level of the Ⅰ1 confined aquifer

图6 第Ⅰ2承压含水层沉降逐年变化量与地下水水位 逐年变化量对比Fig.6 Comparison of annual variation of land subsidence and groundwater level of the Ⅰ2 confined aquifer

从研究场地内各含水层沉降逐年变化量与地下水水位逐年变化量的对比结果来看，地面沉降变化量与地下水水位标高变化量数值在各监测年份存在着明显的对应关系，且后续的地面沉降与地下水水位之间的回归分析在数理上也充分证明了地面沉降量与地下水水位变化之间存在密切的相关性。

3 地面沉降量与地下水水位的回归分析及预测

由前述理论分析和地下水水位监测点数据分析可知，地面沉降量与地下水水位的变化之间存在线性关系，可以用线性回归方程来描述。本文基于数理统计方法，建立时间序列上地面沉降量与各含水层地下水水位变幅之间的多元线性回归模型，以此为基础，可以实现地下水开采引起的地面沉降量预测。

3.1 地面沉降量与地下水水位变化之间的多元线性回归模型建立

通过对计算点多年统计资料的分析，本文建立了研究场地内地面沉降量与地下水水位变化之间的多元线性回归模型：

Δ

b=α

+

α

Δ

H

+

α

Δ

H

+

α

Δ

H

+

α

Δ

H

+

α

Δ

H

+

α

Δ

H

(15)

式中：Δ

b

为月地面沉降量(mm)；Δ

H

为潜水含水层月地下水水位变幅(m)；Δ

H

为潜水含水层与浅部孔隙承压含水层间黏性土弱含水层月地下水水位变幅(m)； Δ

H

为浅部孔隙承压含水层月地下水水位变幅(m)； Δ

H

为浅部孔隙承压含水层与第Ⅰ承压含水层间黏性土弱含水层月地下水水位变幅(m)；Δ

H

为第Ⅰ承压含水层月地下水水位变幅(m)；Δ

H

为第Ⅰ承压含水层月地下水水位变幅(m)；

α

为常数项，与各含水层和黏性土弱含水层的监测控制程度和监测精度以及非地下水开采引起的地面沉降有关；

α

、

α

、

α

、

α

、

α

、

α

为系数项，与各含水层和黏性土弱含水层的土体骨架释水系数有关。

根据已有266组因变量(月地面沉降量)与自变量(各含水层地下水水位变幅)的观测统计数据，经计算得到了研究场地内月地面沉降量与各含水层地下水水位变幅之间的多元线性回归方程：

Δ

b=

-0.87+1.22Δ

H

+0.46Δ

H

+2.61Δ

H

+0.32Δ

H

+0.63Δ

H

+ 0.83Δ

H

(

16

)

3.2 模型检验

本文所建立的多元线性回归模型的拟合度检验结果，详见表1。

表1 多元线性回归模型拟合度检验结果Table 1 List of goodness of fit test of the multiple linearregression model

由表1可知，建立的多元线性回归模型的复相关系数

R

为0.917，表明模型自变量与因变量之间的密切程度很高；模型的决定系数(也称判定系数)

R

值为0.841，为避免随自变量个数增加其可靠性降低，经调整后

R

值为0.837(统计学上一般

R

值大于0.8时说明其拟合程度较高)，表明利用该多元线性回归方程来描述和说明因变量的变化所解释的程度较高；而模型

R

的估计标准误差值为2.682 26，其值较小，表明

R

的估值具有一定的可靠性。

本文所建立的多元线性回归模型的方差分析结果，见表2。

表2 多元线性回归模型方差分析结果Table 2 List of ANOVA of the multiple linear regressionmodel

由表2可知，建立的多元回归模型的显著性指标Sig.值为0，

F

分布统计量值为195.534，说明该模型具有高度显著的统计意义。

本文所建立的多元线性回归模型的共线性检验结果，见表3。

表3 多元线性回归模型共线性检验结果Table 3 List of collinearity tests of the multiple linearregression model

由表3可知，建立的多元线性回归模型的特征值均不为0(若多个维度的特征值等于0，则可能存在共线性问题)，条件指数值均小于30(若某个维度的条件指数大于30，则存在共线性问题)，说明该模型各自变量间存在共线性问题的可能性很小。

本文所建立的多元线性回归模型的残差分析结果，见表4。

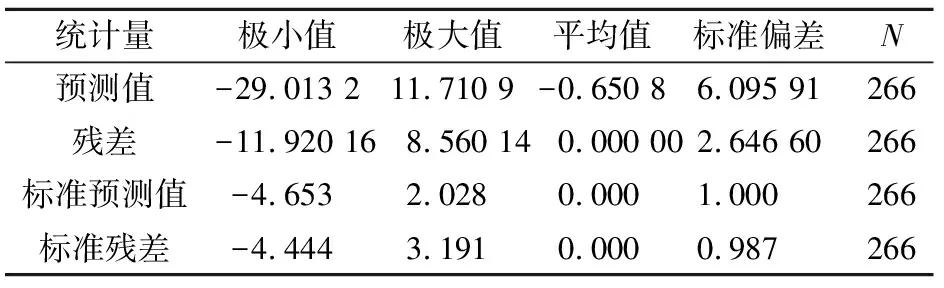
表4 多元线性回归模型残差分析结果Table 4 List of residual statistics of the multiple linearregression model

由表4可知，建立的多元线性回归模型的残差统计量数据中无离群值，且数据的标准残差也较小，可以认为该模型是健康的。

通过对本文所建立的多元线性回归模型的检验，绘制了标准化残差的直方图和标准化残差的正态

P

-

P

图，见图7和图8。

图7 标准化残差直方图Fig.7 Histogram of standardized residuals

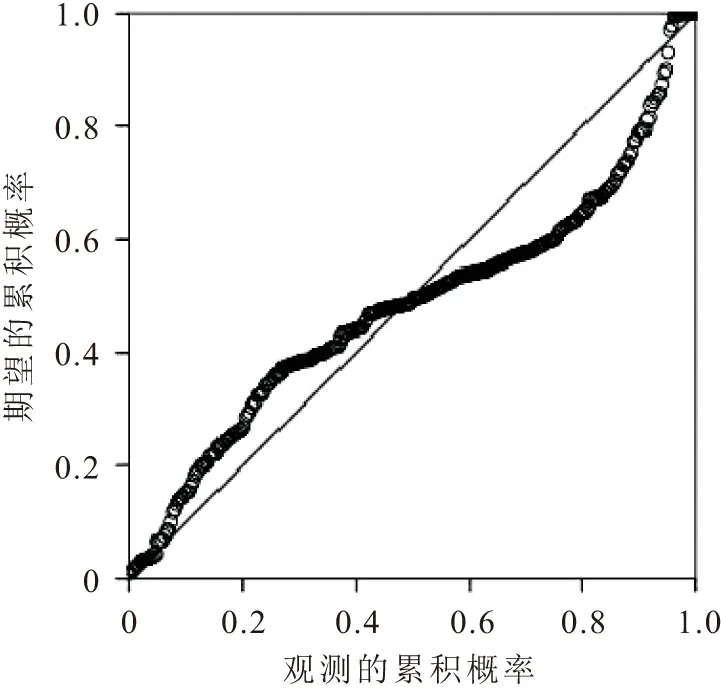
图8 标准化残差正态P-P图Fig.8 Normalized residual normal P-P diagram

由图7和图8可见，建立的多元线性回归模型的标准化残差分布具有正态分布的趋势，说明模型是恰当、可用的。

综上所述，本文所建立的多元线性回归模型正确、可信，可以用来预测某处地面沉降总量月变化量的发展趋势。

4 结 论

(1) 由地下水开采引起的地面沉降，地面沉降量与地下水水位变化之间存在时间上的对应，通过对地面沉降机理的研究证实两者之间确实存在线性相关关系。本文应用数理统计方法，通过工程实例对地面沉降与地下水水位进行了回归分析及预测，模型检验结果表明该预测模型是可用的。

(2) 在未来地下水开发利用规划情况下，场地所在地区可应用该方法开展由地下水开采引起的地面沉降量预测，其计算速度快、实用性较高。

(3) 随着全国范围内地下水与地面沉降监测网的逐年完善，大量精度较高的监测数据将被获取与积累。本文的研究方法可在第四纪松散沉积层较厚的冲、洪积平原地区进行广泛的推广与应用。