基于Xgboost的Ebay网上拍卖最终成交价格预测

摘  要： 对成交价格进行预测，旨在获得Ebay拍卖品的价格动态，使买卖双方更好地进行交易。将价格区间进行多分类划分和多次最优参数选择，建立极端梯度提升（XGBoost，eXtreme Gradient Boosting）模型，并与最优逻辑斯蒂回归模型比较，使用平均准确率作为模型的评估指标。经比较发现XGBoost模型达到90.55%的准确率，明显优于逻辑斯蒂回归模型。此外通过十次迭代，分别得到两个模型的准确率变化趋势，结果显示Xgboost具有更高的准确率。

关键词： Ebay网上拍卖; 成交价格预测; 多分类; 极端梯度提升; 最优参数选择; 逻辑斯蒂回归

中图分类号：TP393          文献标识码：A     文章编号：1006-8228（2021）01-46-05

Prediction of the final price of Ebay online auction using XGBoost

Cao Feifei

（School of Economics， Guangdong Peizheng University， Guangzhou， Guangdong 510830， China）

Abstract： To predict the transaction price， aiming to obtain the price dynamics of Ebay auction products， so that buyers and sellers can better conduct transactions. By multi-classifying the price interval and multiple optimal parameter selecting， the XGBoost （eXtreme Gradient Boosting） model is established， and compared it with the optimal logistic regression， using the average accuracy as the evaluation index. The comparison finds the XGBoost model achieved 90.55% accuracy， which is significantly better than the logistic regression model. In addition， through ten iterations， the accuracy trends of the two models are obtained respectively， the result shows that XGBoost has higher accuracy.

Key words： Ebay online auction; transaction price prediction; multi-classification; eXtreme Gradient Boosting; optimal parameter selection; logistic regression

0 引言

互联网的飞速发展使我们的生活真正产生日新月异的变换，不知不觉改变人们的生活习惯，网上拍卖市场就是众多改变之一[1]。由于网上拍卖的流行， 许多大型拍卖网站应运而生，比如熟知的Yahoo拍卖、露天拍卖、台湾樂天市场、Ebay、DMM.com等[2]，他们对电子商务的集体影响是惊人的，其中Ebay是发展最迅速，也是目前为止世界上最大的网上拍卖网站。据统计，Ebay网站上有1.49亿活跃买家[3]，几乎任何人都可以买卖任何东西，超过7亿商品在Ebay进行交易。作为世界上最大的网上交易平台，Ebay产生了大量的交易数据，各类交易数据都包含大量有用的交易信息[4]，因此对这些交易数据的研究就显得尤为重要。

通过对拍卖数据的研究，为出标者和投标者制定一套切实可用的竞价策略，出标者能尽可能得到想要的价格，中标者也可以最划算的价格拍到自己想要的物品，实现共赢。由于拍卖过程的动态性，即随时间的变化，拍卖过程没有规律可循，造成实际操作不容易预测。本文在前人研究的基础上使用机器学习算法，对拍卖数据集进行预处理和指标体系构建，然后对成交价格进行预测，我们希望机器学习方法能在拍卖数据方面体现它们的价值，这也是本文的另一个目的。

1 相关工作

目前，对于最终成交价格的预测研究都是通过对历史数据收集，找到它们之间的规律，然后通过建立模型进行预测。

国外有代表性的研究如下：Wang、Jank和Shmueli用函数型数据分析（FDA）对最终成交价格预测，并对拍卖动态性进行了解释[5]。Zhang，Jank和Shmueli提出了一种动态预测模型，此外他们也使用函数型K最近临对拍卖动态数据进行了预测，他们先使用Beta模型拟合出三个不同的价格走势，这样就得到Beta累积分布函数，通过对Beta累积分布函数分别求一阶导数和二阶导数作为价格的速度和加速度，然后使用函数型K最近临预测价格走势[6]。Liu，Feng和Shao通过对投标者行为的分析，他们提出了基于Bagging算法和决策树算法的模型去预测成交价格[7]。相比国外， 国内对于最终成交价格的动态性的研究很少，主要有：李雪峰等人使用机器学习算法对Ebay网站上的诺基亚移动手机数据进行最终成交价格的预测，他们将最终成交价格分为连续型和离散型两种类型，并分别应用不同的机器学习算法进行预测。连续型的最终价格预测使用多元回归算法，离散型价格预测使用使用逻辑斯蒂回归和神经网络算法，除此之外，他们还认为聚类分析也会对预测的准确率造成影。杨睿等基于函数型回归模型建立了网络拍卖品的动态预测模型。

2 数据收集及预处理

2.1 数据收集

本文所用的数据集是通过网络爬虫技术获得的。文章对Ebay拍卖网站的历史交易数据建立爬虫模型，并对历史数据进行实时跟踪，获取有用的信息， 然后将爬取的数据保存到数据库中。此数据集是关于Microsoft Box的数据，它在Ebay拍卖网站上非常流行，产生了大量的交易数据，总共有1861个拍卖数据，拍卖长度都是七天。

2.2 数据预处理

2.2.1 数据重编码

因为数据集中条件（Condition）这一列是字符串形式的，所以在建模之前将其重编码为0，1变量，并记为Condition1;对于拍卖开始时间（StartTime），投标时间（BidTime）和投标结束时间（EndTime），它们都是时间戳形式的数据，我们将其转换成数值形式，并生成三个新变量分别记为startday，bidday和endday。

2.2.2 缺失值处理

此数据集中邮费这一属性包含缺失值，所以对其进行填充，本文采用K最近邻法填充缺失值，因为基于K个最近邻的缺失值填充算法考虑到了属性上下数据之间的相关性，可以使预测结果更为准确，我们使用R语言来完成。

具体做法如下：首先计算目标属性与其他属性之间的欧式距离，其次在所有计算出来的距离中找到距离目标属性距离最小K个最近邻邮费，然后对选择出的K个最近邻目标属性赋予相应的权值，其相应位置的加权平均值即为目标属性缺失值的估计值。填充完缺失值后，生成新的邮费变量记为ShipFee1。

2.2.3 数据标准化

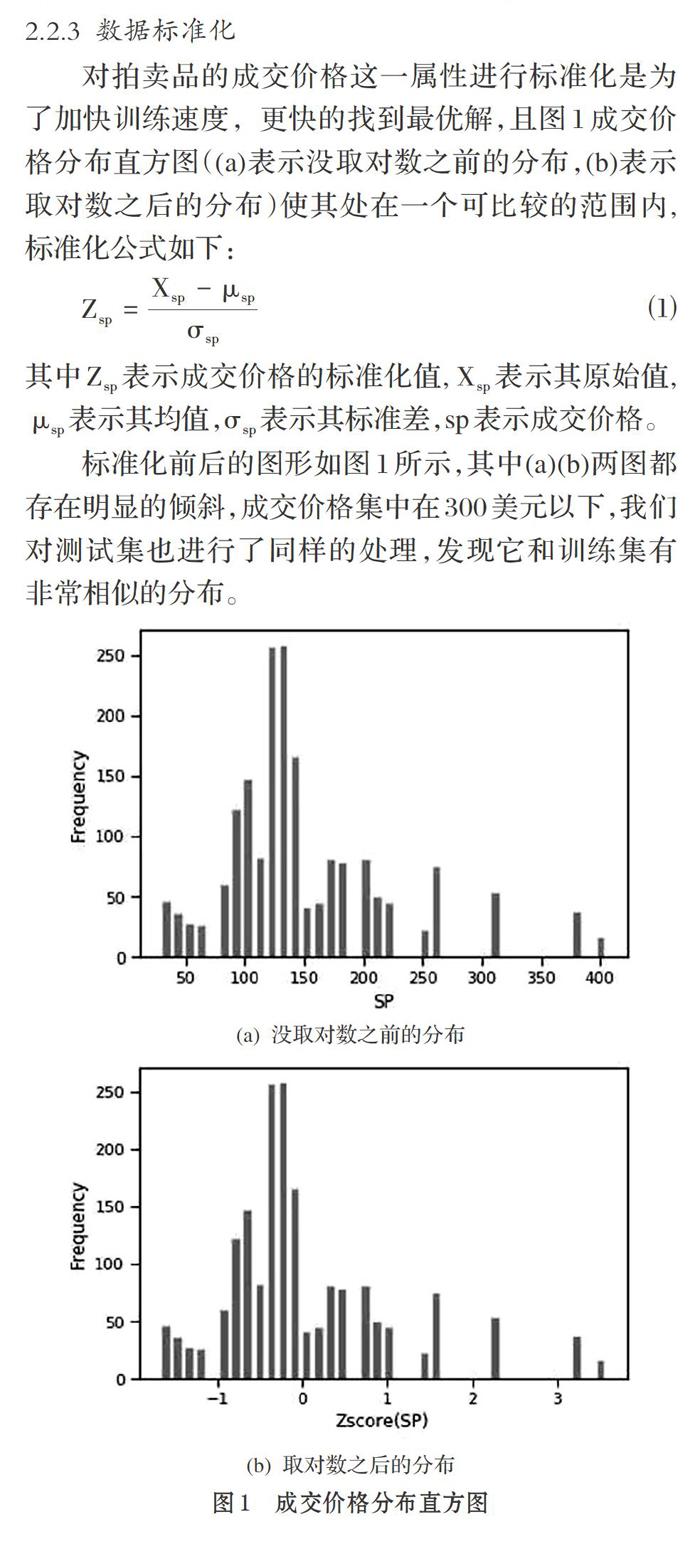
对拍卖品的成交价格这一属性进行标准化是为了加快训练速度， 更快的找到最优解，且图1成交价格分布直方图（（a）表示没取对数之前的分布，（b）表示取对数之后的分布）使其处在一个可比较的范围内， 标准化公式如下：

[Zsp=Xsp-μspσsp]  ⑴

其中[Zsp]表示成交价格的标准化值，[ Xsp]表示其原始值，[ μsp]表示其均值，[σsp]表示其标准差，sp表示成交价格。

标准化前后的图形如图1所示，其中（a）（b）两图都存在明显的倾斜，成交价格集中在300美元以下，我们对测试集也进行了同样的处理，发现它和训练集有非常相似的分布。

3 属性构建和选择

3.1 属性构建

由于拍卖数据和投标数据是一个拍卖记录对应多个投标记录，且他们之间相互依赖，为了使用机器学习算法更准确的建立模型，需将一对多关系转换为一对一的关系。我们使用李雪峰等提出的方法进行属性的构建与选择[9]。

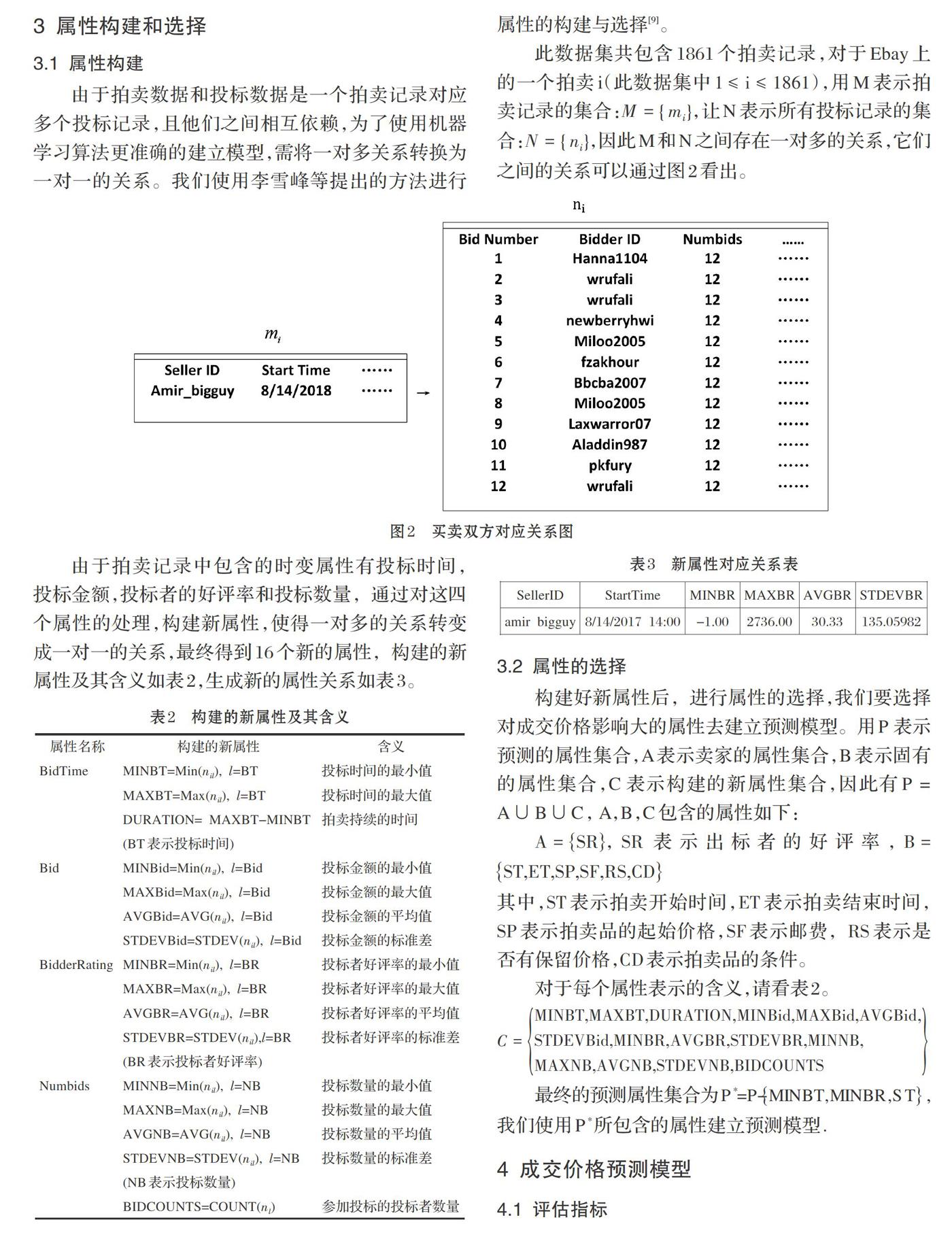
此数据集共包含1861个拍卖记录，对于Ebay上的一个拍卖i（此数据集中[1≤i≤1861]），用M表示拍卖记录的集合：[M={mi}]，让N表示所有投标记录的集合：[N={ni}]，因此M和N之间存在一对多的关系，它们之间的关系可以通过图2看出。

由于拍卖记录中包含的时变属性有投标时间， 投标金额，投标者的好评率和投标数量， 通过对这四个属性的处理，构建新属性，使得一对多的关系转变成一对一的关系，最终得到16个新的属性， 构建的新属性及其含义如表2，生成新的属性关系如表3。

3.2 属性的选择

构建好新属性后， 进行属性的选择，我们要选择对成交价格影响大的属性去建立预测模型。用[P]表示预测的属性集合，[A]表示卖家的属性集合，[B]表示固有的属性集合，[C]表示构建的新属性集合，因此有[P=A∪B∪C]，[ A]，[B]，[C]包含的属性如下：

[A=SR]，[SR]表示出标者的好评率，[B=ST，ET，SP，SF，RS，CD]

其中，[ST]表示拍卖开始时间，[ET]表示拍卖结束时间，[SP]表示拍卖品的起始价格，[SF]表示邮费， [RS]表示是否有保留价格，[CD]表示拍卖品的条件。

对于每个属性表示的含义，请看表2。

[C=MINBT，MAXBT，DURATION，MINBid，MAXBid，AVGBid，STDEVBid，MINBR，AVGBR，STDEVBR，MINNB，MAXNB，AVGNB，STDEVNB，BIDCOUNTS]

最终的预测属性集合为[P*=P-MINBT，MINBR，ST]， 我们使用[P*]所包含的属性建立预测模型.

4 成交价格预测模型

4.1 评估指标

对于多分类预测模型，使用平均准确率（AvgAccuracy）作为评估指标，我们先给出准确率（[Accuracyi]）的计算公式：

[Accuracyi=niN×100%，i∈[1，10]]  ⑵

由⑵式可得到平均准确率（[AvgAccuracy]）的计算公式：

[AvgAccuracy=110i=110Accuracyi×100%] ⑶

其中[ni]表示每次正确预测的样本量，[N]表示每次预测的样本总量。

4.2 实验结果

预测之前， 将此数据集记为[S]，使用交叉验证法先将拍卖数据集划分为10个大小相同的互斥子集，即[S=S1∪S2∪S3∪…∪S9，Si∩Sj≠?（i≠j，i，j∈1，10）]，要求每个子集[Si]都能保持一致的数据分布，然后每次用9个子集的并集作为训练集，余下的那个子集作为测试集，得到10组训练/测试集，这样可以对数据集进行10次训练和测试，最终得到这10个测试结果的平均值。

极端梯度提升是梯度提升树的改进，用极端梯度提升进行多分类预测时，使用负对数似然损失函数（[-LogLoss]）作为最优极端梯度提升模型的衡量指标， 该函数的值越小，则模型的预测效果越好。本文选取树的最大深度（[maxdepth]），学习率（[learning_rate]），拟合提升树的数量（[n_estimators]），这三個参数建立极端梯度提升模型，并使用网格搜索进行参数的调整，选择最优的参数，建立最佳的模型，下面给出实验结果。

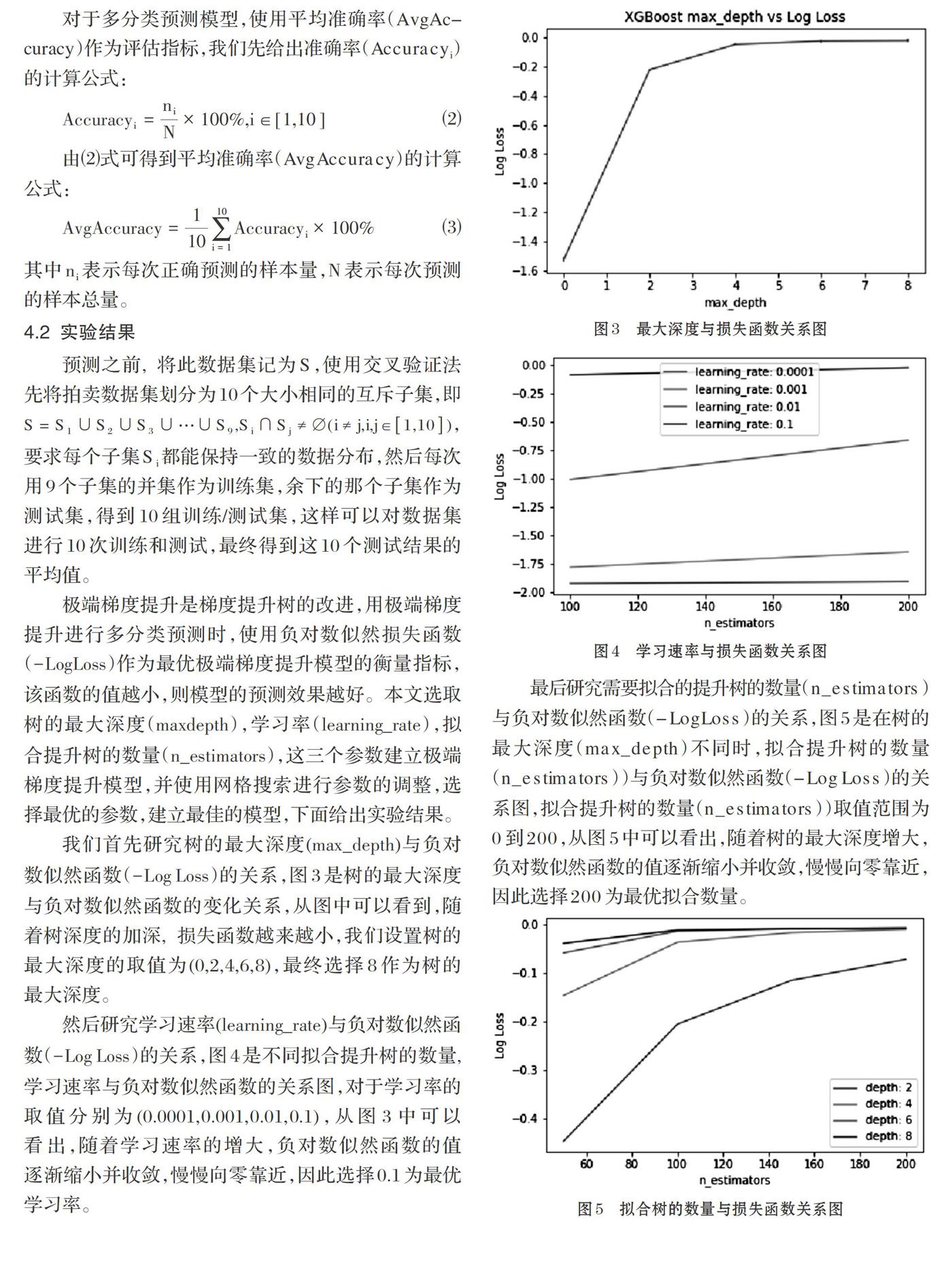
我们首先研究树的最大深度（[max_depth]）与负对数似然函数（[-Log Loss]）的关系，图3是树的最大深度与负对数似然函数的变化关系，从图中可以看到，随着树深度的加深， 损失函数越来越小，我们设置树的最大深度的取值为（0，2，4，6，8），最终选择8作为树的最大深度。

然后研究学习速率（[learning_rate]）与负对数似然函数（[-Log Loss]）的关系，图4是不同拟合提升树的数量， 学习速率与负对数似然函数的关系图，对于学习率的取值分别为（0.0001，0.001，0.01，0.1），从图3中可以看出，随着学习速率的增大，负对数似然函数的值逐渐缩小并收敛，慢慢向零靠近，因此选择0.1为最优学习率。

最后研究需要拟合的提升树的数量（[n_estimators]）与负对数似然函数（[- LogLoss]）的关系，图5是在树的最大深度（[max_depth]）不同时，拟合提升树的数量（[n_estimators]））与负对数似然函数（[- Log Loss]）的关系图，拟合提升树的数量（[n_estimators]））取值范围为[0]到[200]，从图5中可以看出，随着树的最大深度增大，负对数似然函数的值逐渐缩小并收敛，慢慢向零靠近，因此选择[200]为最优拟合数量。

通过对这三个参数的调整，选择，最终得到了最优训练模型，将该模型运行在之前已经划分好的[10]个训练/测试数据集上，最终得到的平均准确率为[90.55%]

4.3 模型评估

现在将极端梯度提升预测模型（[XGBoost]）与最优的逻辑斯蒂回归模型（[LR]）进行比较，迭代[10]次的准确率的变化如图[6]所示，表[4]是这两个模型在10个测试子集上的准确率和平均准确率。从中看出，极端梯度提升模型具有更好的预测效果。

5 结束语

通过数据预处理，清洗以及对属性的构建与选择等一系列工作，本文通过网格搜索选择最优的参数去建立预测模型，在离散型价格预测上取得了较高的准确率。将成交价格划分成间隔相等的区间并建立多分类预测模型，我们认为这种预测方法比较新颖。

在研究过程中，也存在一些缺陷和不足，主要有以下两点：一是此数据集是倾斜的，虽然经过标准化处理，也还是倾斜的，这会对预测准确率造成影响;二是对极端梯度提升模型参数的选择， 挑选了最主要的三个参数进行建模， 并且这三种参数的取值都是自行设置的。

因为本文所用的数据集中并没有包含是否有图片，对拍卖物品的描述等属性，但是研究人员发现这些属性对最终成交价格有明显的影响，基于此可以通过设计一个程序得到这些有用的信息，我们猜想以后的研究可以朝着这一方面发展，从图片和文本中挖掘出对成交价格有用的信息，建立适合多种数据分布类型的预测模型。

参考文献（References）：

[1] 张金城.网上拍卖：电子商务的一种新交易方式[J].审计与经济研究，2002.17（3）：49-51

[2] Kersten G E， Vahidov R， Gimon D. Concession-making in multi-attribute auctions and multi-bilateral negotiations： Theory and experiments[J].Electronic Commerce Research & Applications，2013.12（3）：166-180

[3] Ba S， Whinston A B， Zhang H. Building trust in online auction markets through an economic incentive mechanism[J]. Decision Support Systems，2003.35（3）：273-286

[4] Pinker E J， Seidmann A， Vakrat Y. Managing Online Auctions： Current Business and Research Issues[J]. Management Science，2003.49（11）：1457-1484

[5] Wang S， Jank W， Shmueli G， et al. Modeling Price Dynamics in eBay Auctions Using Differential Equations[J]. Publications of the American Statistical Association，2008.103（483）：1100-1118

[6] Zhang S， Jank W， Shmueli G. Real-time forecasting of online auctions via functional-nearest neighbors[J].International Journal of Forecasting，2010.26（4）：666-683

[7] Liu Y， Feng Y Q， Shao Z. Support System for Predicting Online Auction End Prices[J]. Systems Engineering-Theory Practice，2009.29（12）：134-140

收稿日期：2020-06-19

作者簡介：曹菲菲（1994-），女，甘肃平凉人，理学硕士，专任教师，主要研究方向：统计机器学习。