一种基于时域滤波的红外序列图像去噪算法

周克虎，雷 涛，罗 刚

（1.中国科学院光电技术研究所，四川 成都 610209；2.中国人民解放军63618部队，新疆 库尔勒 841000）

引言

光学设备广泛应用于侦查、测量等领域，现代光学设备一般配置有可见光、红外等多种波段的探测器，其最终的成像效果受光学系统设计、探测器性能、场景光照条件以及环境温度等诸多因素的影响。但对于用户或设备操作人员，其对于成像效果好坏的感受则直接来源于最终的图像显示效果好坏。红外探测器在光学设备中一般承担着目标捕获和高精度位置测量的功能，其图像经常需回传指挥中心进行实时显示。因此，红外图像显示效果的优化对于提升设备的成像质量以及用户体验有着重要的意义。

在实际项目中，探测器噪声导致的红外图像显示效果恶化严重影响了设备的成像质量。常见的红外图像去噪方法主要分为空域方法和变换域方法。空域滤波主要是利用噪声空间分布的随机性，传统的方法有均值滤波、高斯滤波等。这类空域滤波算法会导致图像中边缘和纹理的退化，导致表征图像细节信息的关键梯度数据丢失，输出图像整体表现出模糊感。Tomasi等人提出了一种利用灰度距离进行权值修正的空域高斯滤波算法，称为双边滤波（bilateral filter）[1-4]。该算法不仅能够去掉噪声，还能够保持边缘，解决了传统空域滤波算法导致的图像模糊，在很多场合下表现出了较好的去噪效果。但是，该算法没有利用图像时域的相关性，无法去除序列图像显示时噪声引起的帧间灰度随机变化，其时域去噪效果有待提升。

区别于直接的空间邻域滤波，非局部均值（non-local means，NLM）滤波算法[5-8]通过图像中多个相似图像块的像素值加权平均进行无噪声图像估计，能较好地去除图像中的高斯噪声并且能够保持边缘。但是该算法计算复杂度高，限制了其在实时显示场合的使用。

基于变换域的红外图像去噪方法主要有基于小波变换的方法[9-12]、基于快速傅里叶变换（fast fourier transform, FFT）的方法以及基于离散余弦变换（discrete cosine transform，DCT）的 方 法 等。BM3D（block-matching and 3D filtering）算法[13-14]结合空域NLM算法和变换域去噪方法，通过块匹配和三维变换域滤波进行无噪声图像估计，在保持图像边缘的前提下，实现了优良的去噪效果。但该计算复杂度高，难以实时显示。

此外，随着深度学习在计算机视觉领域不断取得突破性进展，深度学习技术在图像去噪领域获得了极大的关注[15]，同时也涌现了很多优秀的算法[16-18]。

在光学设备图像实时显示等应用场景中，图像去噪算法的实时性以及去噪效果均十分重要。本文算法是受双边滤波算法的启发，将空域双边滤波算法的核心思想应用至时域，摒弃了传统视频去噪时的运动估计流程[19-20]，不仅具有很高的实时性，而且实现了较好的红外序列图像去噪效果。

1 双边滤波介绍

双边滤波利用邻域像素点的信息来估计当前像素点的灰度值，以消除噪声的影响，实现空域去噪。其核心思想是在分配空间邻域像素点的滤波权值时同时考虑空间距离和灰度差异，以保证滤波窗口内，与待估计像素点的空间距离越近权值越高，与待估计像素点的灰度值差异越小权值越高。

双边滤波定义如下：

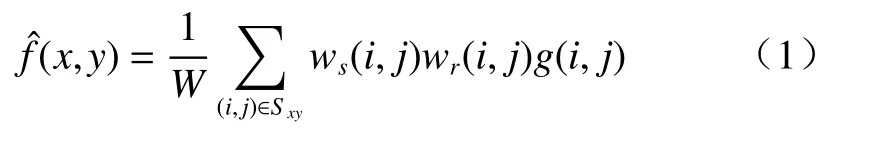
双边滤波的滤波核权值由2个高斯函数的值ws(i,j)和wr(i,j)相乘得到，这里分别称为空间距离高斯函数和灰度距离高斯函数。对于 (i,j)∈Sxy，定义如下：

对于(2)式，像素位置 (i,j)距离当前滤波像素位置 (x,y)的距离越近，权值越大；反之，则权值越小。而对于(3)式，邻域像素位置的灰度值g(i,j)与当前滤波像素点的灰度值g(x,y)的差异越小，权值越大；反之，则权值越小。

分析可知，当 σr→∞时双边滤波退化为一般的空域高斯滤波。因此，双边滤波的实质是引入了滤波邻域内像素灰度值的影响，对高斯滤波的权值进行了修正，使得在进行当前像素点灰度值估计时，灰度值差异大的邻域像素点权值降低。由于视觉上的图像边缘实质为灰度值的较大变化，上述过程在完成了空域去噪的同时，又很好地保持了边缘。

2 算法原理

对于同一个像素点，其连续帧间的灰度值受噪声影响出现随机变化，这是导致红外序列图像显示效果恶化的关键因素。因此，本文从时域滤波的角度，利用连续历史帧像素灰度值对当前像素点的灰度值进行估计，实现同一像素位置连续帧间灰度值的平滑。此外，为了解决时域滤波导致的运动目标拖尾问题，本文引入历史帧像素灰度值的影响对滤波权值进行修正，避免了时域滤波导致的运动目标拖尾。

2.1 时域滤波去噪

将二维图像g视为时间相关的函数，记为g(t)，则有：

式中：g(t)表示当前时刻的探测器输出图像；f(t)表示无噪声影响的原始图像；n(t)为 噪声；t为用离散的帧编号表示的时间；N为当前已经采集的图像总帧数。

每一个像素点的时域高斯滤波估计值定义如下：

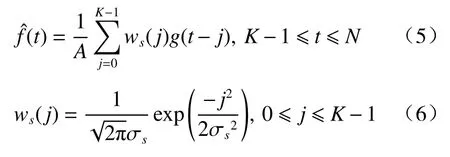
式中：A为 高斯滤波权值归一化的系数；σs为高斯函数的方差；K为滤波帧数。典型地，K=5，σs=5.0时，归一化的高斯滤波权值（即历史5帧的权值）如下：

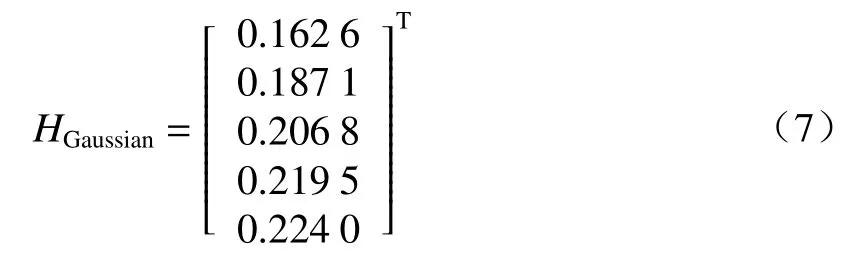
此时的高斯滤波系数实际为半宽的一维高斯核，且当前帧的权值最高，距离当前帧时间越长的帧对应的权值越小。这个过程完成了单个像素点的时域高斯滤波处理，通过逐像素滤波处理实现整个图像帧的时域去噪。

2.2 滤波权值修正

对于静态场景，上述时域高斯滤波去噪方法已经具备使用价值，但是对于动态场景，上述方法同一般的视频去噪方法一样，会导致运动目标拖尾的出现，如图1和图2所示。

序列1为制冷型红外相机拍摄的图像，图像的背景主要为天空及部分地面，运动目标为工作中的风力发电设备，其叶片的帧间运动明显。可以看出，经过时域高斯滤波之后，转动的叶片边缘出现了明显的模糊。序列2中，图像的背景主要为静止输电铁塔及部分天空，运动目标为飞鸟。运动目标的信噪比为5左右，且在帧间存在明显的位移。经过时域滤波后，运动目标不仅形成了明显的拖尾，而且整体呈现出严重模糊。分析其形成原因发现，在时域高斯滤波的过程中，历史帧相同位置的灰度值会参与对当前帧像素值的估计，当历史帧中存在灰度值差异较大的目标时，可能会导致当前帧灰度值估计值偏差大，在运动目标图像上表现为目标的拖尾。

图2 红外序列图像时域高斯滤波去噪效果（序列2）Fig.2 Denoising effect of temporal Gaussian filtering for infrared sequence images (sequence 2)

通过对动态场景进行分析发现，运动目标覆盖的像素点在连续帧间表现出灰度值突变，与空域上的边缘、纹理有一定的相似性，均表现出明显的梯度变化。

受空域双边滤波的启发，引入连续帧灰度值的影响对高斯滤波的权值进行修正。则对于每一个像素点，新的时域高斯滤波估计值定义如下：

式中:WP为修正后的滤波权值归一化系数；同空域双边滤波一样，最终的滤波权值由2个高斯函数的值相乘得到，这里分别称为时间距离高斯函数ws(j)和 灰度距离高斯函数wr(j)，定义如下：

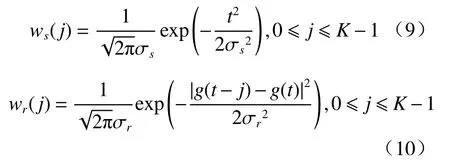
式中：σs为时间距离高斯函数的方差；σr为灰度距离高斯函数的方差。

可以看出，当 σr→∞时(8)式退化为一般的时域高斯滤波，即(5)式。通过增加灰度距离影响的权值修正系数，避免了灰度差异值过大的历史帧像素点参与当前像素点灰度值的估计，从而解决了时域高斯滤波导致的运动目标拖尾问题。

3 实验分析

3.1 去噪效果

时域高斯滤波处理后，红外序列图像中背景区域同一个像素点（取100个固定像素位置，统计连续100帧）连续帧间的灰度方差变化如图3所示。

对于背景区域的同一个像素点，其连续帧间灰度变化越平缓（即均方差越小）则显示效果越好。通过图3可以看出，经过时域滤波后同一像素位置连续帧间的灰度值均方差降为原来的1/2左右，可见噪声导致的连续帧间的灰度随机变化被显著平滑。通过观察时域滤波处理后的显示图像发现，原本帧间动态变化的噪声被明显抑制，显示效果得到了有效提升。

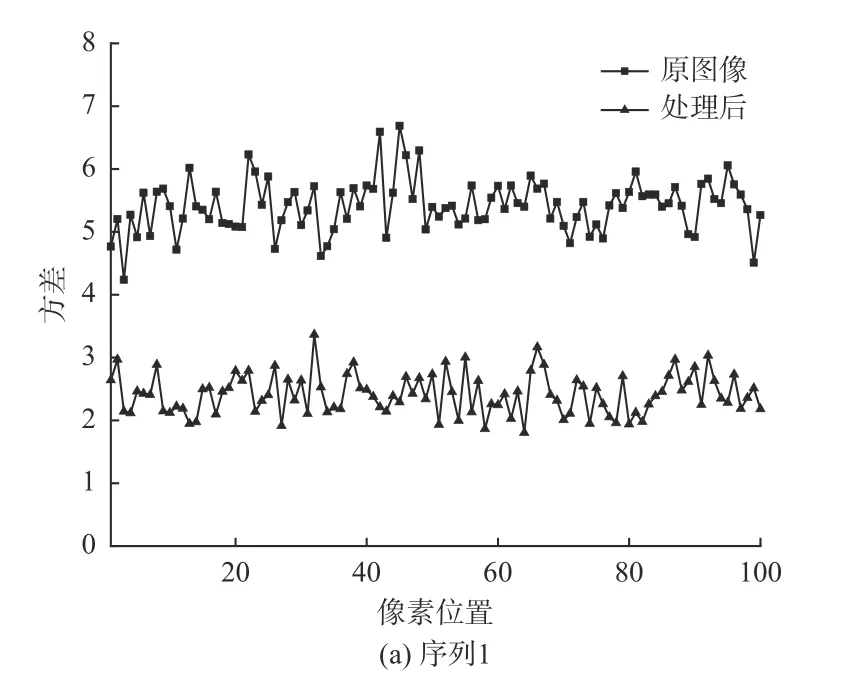
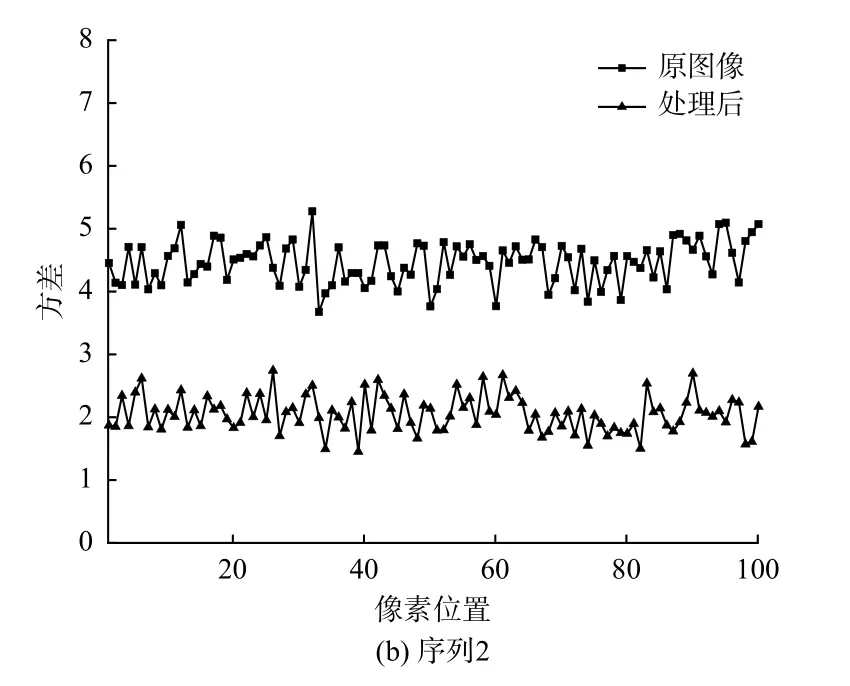
图3 红外序列图像的连续帧灰度值变化方差对比图Fig.3 Comparison diagram of change variance of continuous frame gray values of infrared sequence images

选取有运动目标的场景进行实验，红外序列图像去噪后的效果如图4和图5所示。

图4 不同方法去噪结果对比（序列1）Fig.4 Comparison of denoising results with different methods (sequence 1)

从图4和图5可以看出，使用不同的去噪算法图像中背景部分的噪声均被一定程度地抑制；而风力发电机的叶片边缘以及天空中的飞鸟在去噪后的图像中均比较清晰，没有出现明显的模糊或者拖尾。这说明双边滤波算法、NLM算法、BM3D算法以及本文提出的算法，均有较好的保边去噪效果。

图5 不同方法去噪结果对比（序列2）Fig.5 Comparison of denoising results with different methods (sequence 2)

3.2 定量评价

通过无噪声红外图像叠加零均值高斯噪声来仿真不同噪声水平的含噪图像序列（序列3为室外场景，序列4为室内场景，分别如图6和图7所示），并利用图像去噪领域常用的峰值信噪比（peak signal-to-noise ratio, PSNR）和结构相似性（structural similarity, SSIM）指标对去噪效果进行定量评价。

图6 序列3叠加不同水平的高斯噪声Fig.6 Sequence 3 superimposes different levels of Gaussian noise

对前述的序列3和序列4（图像大小均为640×480像素）进行实验，统计了去噪后的PSNR（见表1和表2）和SSIM（见表3和表4）。

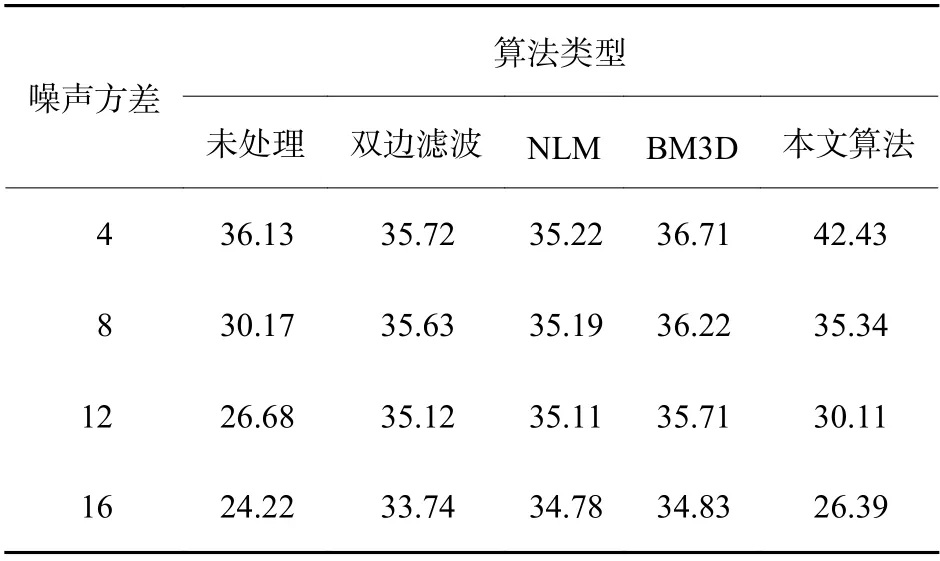
表1 序列3不同算法去噪后的PSNRTable 1 PSNR of sequence 3 after denoising with different algorithms dB

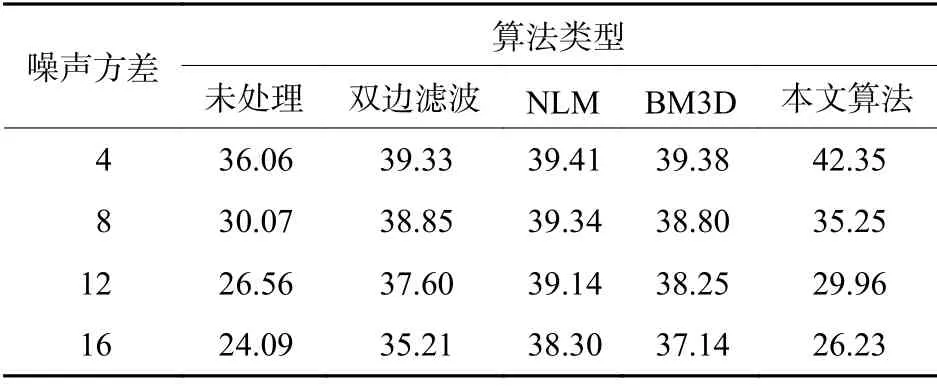
表2 序列4不同算法去噪后的PSNRTable 2 PSNR of sequence 4 after denoising with different algorithms dB

表3 序列3不同算法去噪后的SSIMTable 3 SSIM of sequence 3 after denoising with different algorithms

表4 序列4不同算法去噪后的SSIMTable 4 SSIM of sequence 4 after denoising with different algorithms

统计了不同算法的处理时间（硬件配置：i5-8250U 4核CPU，主频1.8 GHz，内存16 GB），如表5所示。

表5 不同算法的处理时间Table 5 Processing time of different algorithms ms

上述实验中，所有的滤波窗口尺寸均为11×11像素，NLM算法和BM3D算法的模板尺寸为7×7像素，搜索窗口尺寸为21×21像素。

从实验数据中可以看出，对于不同噪声水平的图像序列，4种算法均有效提升了图像的PSNR和SSIM指标，其中NLM算法和BM3D算法的指标提升十分显著。不过对于去噪后的图像（参见图4和图5），NLM算法和BM3D算法会导致图像整体呈现明显失真。这种失真在图5中表现的更加突出，其原因是序列2的背景噪声更加严重。

双边滤波算法和本文算法导致的失真均比较轻微，但是实验发现：双边滤波对单帧图像进行处理，没有利用时域信息，在连续帧显示的场合，噪声导致的连续帧显示效果恶化仍然存在；本文提出的算法有效地利用了图像噪声帧间分布的随机性，通过帧间平滑处理抑制噪声，在红外序列图像显示时取得了良好的效果。

随着噪声水平的提高，可以看到本文算法的效果有所下降，这说明本文算法更加适合低噪声水平的序列图像去噪。此外，NLM算法和BM3D算法的处理时间均超过了4 s（见表5），难以使用在光电成像设备图像显示等实时显示场合。而本文算法实时性高，可以用于序列图像的实时显示。

4 结论

针对噪声导致的红外序列图像显示效果恶化，本文通过历史多帧像素值的加权和对当前帧的像素值进行估计，提出了一种基于时域滤波的噪声抑制方法。进一步，为了解决时域滤波导致图像中运动目标产生拖尾和模糊的问题，通过灰度距离高斯函数对时域高斯滤波权值进行修正，避免历史帧灰度值差异大的像素值参与当前灰度值估计。实验表明，本文提出的算法有效地抑制了噪声对于连续帧图像显示的影响，同时也解决了时域滤波导致场景中的运动目标产生拖尾的问题。通过与图像去噪领域的优秀算法进行对比，表明了本文算法在对图像实时显示有需求的光电成像设备等应用场景中，具有较高的实际应用价值。