煤矿砂岩动态力学性能试验与分析方法研究*
汪海波,翟国良,王梦想,宗 琦
(安徽理工大学 土木建筑学院,安徽 淮南 232001)
0 引言
煤炭开采环境大多为沉积岩,典型岩石有砂岩、泥岩、黏土岩等,煤系岩石虽经沉积成岩作用,但强度低,变形大[1],属于软岩;国际岩石力学学会将单轴抗压强度为0.5~25 MPa的岩石定义为地质软岩范畴[2],何满潮[3]认为由于工程部位埋深较深,煤系岩石所受地应力的水平较高,故强度大于25 MPa的岩石也属于软岩范畴。受成岩过程影响,煤系软岩岩性颗粒大小不均,矿物成分多样,胶结质差,加之沉积成岩过程复杂,岩石存在大量微结构面,造成岩石波阻抗较小,使岩体应力传播和能量传递发生较大改变。同时,随着煤矿开采逐渐进入深部,由于具有“三高一扰动”的特性[4-5],岩石处于1种复杂受力状态,巷道的大变形、高地压和难支护等工程灾害现象日趋增多;矿井冲击地压、掘进爆破、矿压显现加剧等也均体现对岩石的动作用[6-7]。煤系岩石的动态力学性能研究日益增多,平琦等[8]利用SHPB(霍普金森压杆)试验装置对煤矿岩石进行动态试验,发现试件动态抗压强度与应变率具有较强的相关性;李晓峰等[9]开展灰岩、白云岩和砂岩动态冲击试验,研究试件耗散能密度及破碎尺寸与应变率的变化关系;王梦想等[10]开展典型煤矿泥岩的动态力学特性和破裂破碎特征试验,结果表明试件的动态单轴抗压强度随着应变率的增加呈现指数型增长,表现出强应变率效应。以上煤系岩石的冲击试验研究均采用电阻应变片。在SHPB试验中,应力波的传播符合一维应力传播规律,杆的密度与波速较高,即波阻抗较高,而煤系软岩波阻抗较低,在冲击过程中,应力波从高波阻抗材料传递到低波阻抗材料会产生强烈的反射应力波,根据能量守恒定律,透射波信号会变小,同时,软岩试件在应力波的作用下,产生破裂破碎并会消耗一部分能量,使得透过软岩试件传递到投射杆中的应力波值更小,电阻应变片采集到的数据容易失真。
应变测量技术是SHPB试验系统动态采集的关键技术[11],当被测信号十分微弱时,特别是干扰信号与被测信号相当时,电阻应变片测量精度大大降低,半导体应变片灵敏系数更高,能够提高测量精度[12],虽然半导体应变片技术存在非线性及拉压不对称等不足,但随着数据处理精度的提高,这种不足也在慢慢减小。胡时胜等[13]利用半导体应变片与电阻应变片同时测量纯铝的动态应力应变关系,所测结果十分相近;赵磊等[14]针对芳纶绸布材料,进行试样两端应力平衡、实验速度、半导体应变片与电阻应变片测量的验证;汪海波等[15]、袁璞等[16]分别采用半导体应变片对硬煤、泡沫混凝土冲击试验过程中的透射应力波进行测试。
对于岩石材料动态冲击,由于岩石强度较高,采用半导体应变片测试时,很容易出现超载;在煤试件冲击过程中,由于透射波信号较弱,电阻应变片又较难采集。现有文献多采用同种应变片,数据处理也是针对同种应变片测试数据,而不同种类应变片测量数据交互处理对计算结果的影响及影响程度问题鲜有文献研究。综上所述,本文通过在透射杆上粘贴半导体应变片与电阻应变片并分别采集透射波信号,选择淮北矿区某煤矿埋深-690 m的砂岩为软岩代表,开展直径50 mm SHPB冲击压缩试验,采用二波法、三波法和简化三波法处理电阻应变片与半导体应变测量数据,从砂岩试件应力应变曲线、应变率和能量耗散角度分析应变片种类和分析方法的精度与差异。
1 试验装置及原理
1.1 试验装置及试件制备
试验采用安徽理工大学直径50 mm变截面SHPB试验装置,撞击杆长度为0.60 m,入射杆和透射杆长度分别为2.40 m和1.20 m。各杆均为同材质合金钢,密度为7.8 g/cm3,弹性模量为210 GPa,纵波波速为5 190 m/s。
试验采用BX120-3AA型电阻应变片,电阻值为(119.8±0.1) Ω、灵敏系数为2.08%±1%;HU-101B-120型半导体应变片,电阻值为(120±5%)Ω、灵敏系数为110%±5%。
通常要求应变片标长l≤(λ/20~λ/10),其中,λ为脉冲信号波长,在SHPB冲击试验中脉冲信号波长λ≥200 mm,所选应变片能够满足动态测量精度要求。
试验选取完整性和均质性较好的砂岩作为研究对象。测得砂岩的密度2.60 g/cm3、纵波波速3 600 m/s、单轴抗压强度30.67 MPa、抗拉强度3.16 MPa、泊松比0.25。
对岩块钻取、切割,打磨成圆柱形试件,文献[17]表明,为减小试件惯性效应,SHPB试验中试件长径比一般控制在0.5左右[17]。将岩石加工成Φ50 mm×25 mm的圆柱形试件,砂岩试件两端表面不平行度小于0.05 mm,面平整度小于0.02 mm。试件安装前,在试件和2压杆端面接触处均匀涂抹薄层的凡士林润滑剂,减少岩石试件和杆端面之间的摩擦阻力,降低加载端面约束力对试件应力状态分布的影响。试验时,确保试样与2杆同轴。
1.2 应变片工作原理
在SHPB试验中,应变信号的测量采用应变片法,将应变片粘贴在基体材料上,电阻应变的电阻随物理形变而产生阻值变化,电阻值计算如式(1)所示[18]:
(1)
式中:R为电阻值,Ω;ρ为金属导体的电阻率,Ω·mm2/m;S为导体的横截面积,mm2;L为导体的长度,m。
当发生变形时,其电阻相对变化量如式(2)所示:
(2)
式中:ΔR为电阻变化值,Ω;dρ为金属导体的电阻率的变化值,Ω·mm2/m;dL为金属导体长度变化值,m;dS为金属导体横截面积变化值,mm2。
半导体应变片利用半导体单晶体的压阻效应将被测部件的应力转化为电阻变化的1种力—电转化原件,压阻效应的大小用压阻系数来表示,在当半导体应变片承受纵向和横向应力时,半导体应变片相对电阻率计算如式(3)所示[19]:
(3)
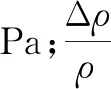
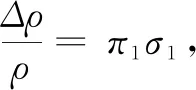
应变片材料电阻的相对变化与应变之间关系如式(4)所示:
(4)
式中:ν为材料的泊松比;π为材料的压阻系数;K为应变片灵敏系数。
由灵敏系数K=1+2ν+πE可知材料的灵敏系数由2个因素决定,其中,1+2ν是由材料几何尺寸改变引起的,πE由材料受力后电阻率变化引起的。一般的金属应变片πE很小,可以忽略。所以金属电阻应变片的灵敏系数较小,K值为1.5~2;半导体应变片的压阻系数很大,K值主要由πE决定,其灵敏系数110%,是电阻应变片灵敏系数2.08%的52.88倍。
1.3 SHPB试验系统应力波透反射系数
SHPB加载试验过程中应力波传播示意如图1所示[20],其中ls为试件高度,mm;L1,L2分别为入射杆应变片、透射杆应变片到试件接触杆端的距离,mm;A1,A2分别表示试件与入射杆、透射杆的接触面;λ为反射系数;σ为应力幅值;SI为入射波;SR为反射波;ST为透射波。
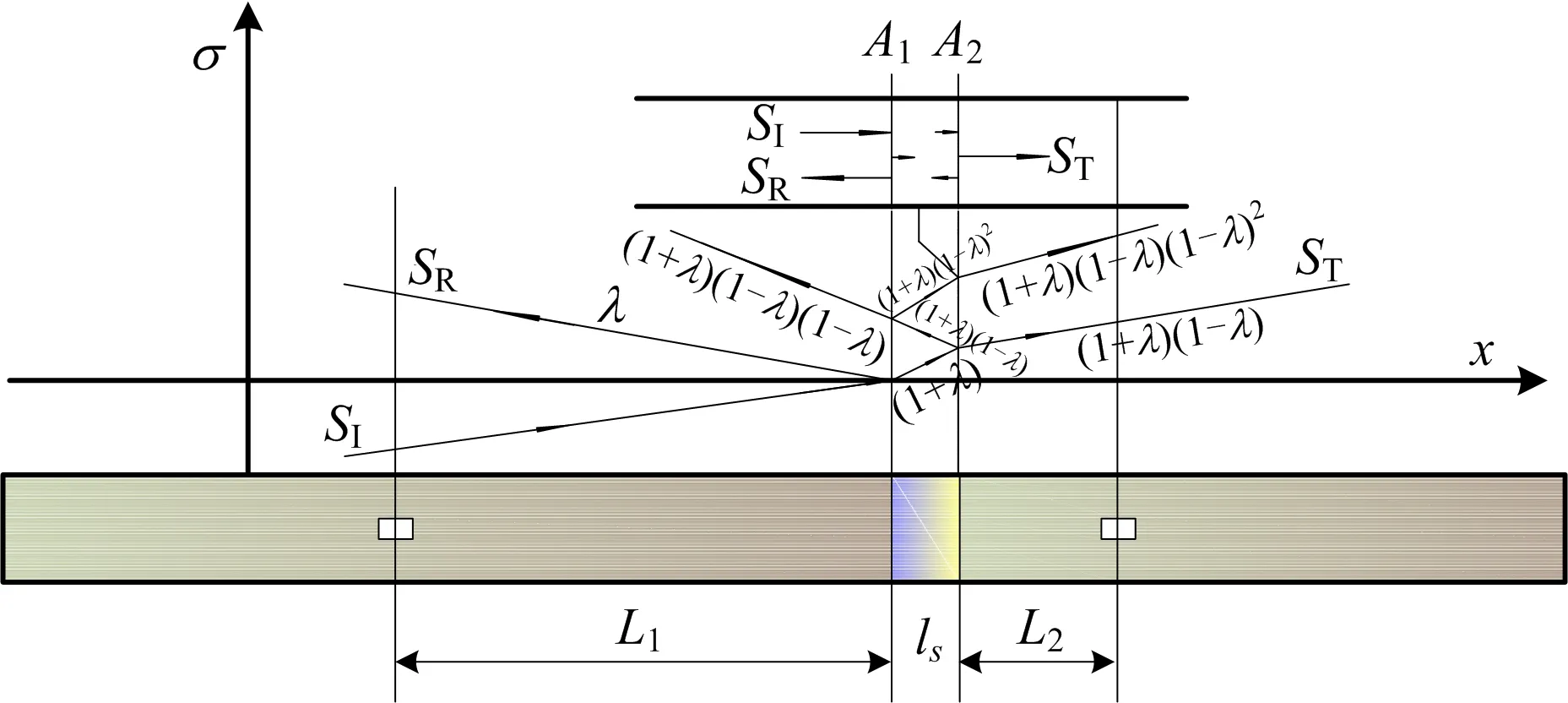
图1 SHPB加载过程中应力波传播示意
当入射波应力幅值为σI的弹性强间断应力波从左向右由压杆向岩石试件传播时,将会在2种介质的界面上形成向左传播的反射波和向右传播的透射波,根据文献[20]所述,应力波在界面的透反射过程满足式(5):
(5)
式中:σI为入射应力波强度,MPa;σR为反射应力波强度,MPa;σT为透射应力波强度,MPa;λ1>2为应力波从第1介质进入第2介质的反射系数;1+λ1>2为透射系数。同理当应力波从第2介质进入第1介质时的反射系数为-λ1>2,透射系数为1-λ1>2;ρS,ρ0分别为岩石试件、压杆的密度,kg/m3;CS,C0分别为岩石试件、压杆的纵波波速,m/s。压杆波阻抗与砂岩波阻抗比为4.33,则反射系数λ1>2为-0.63,透射系数为0.37,透射信号偏弱。
1.4 SHPB试验数据处理方法
目前SHPB试验的数据处理方法常采用二波法、三波法和简化三波法[21-22],其中,二波法处理数据过程简单,若试件受力处于应力平衡状态,结果较可靠;三波法处理结果具有最好可靠性;简化三波法的原理为应变计算采用三波法、应力计算用透射波来计算。
为定量描述岩石破碎试验时吸收能量的大小和岩石破碎过程中能量的耗散情况,杆上的入射能WI(t)、透射能WT(t)和反射能WR(t)可按式(6)~(8)计算[20]:
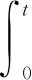
(6)
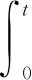
(7)
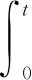
(8)
则试件破坏所吸收的能量Ws计算如式(9)所示:
WS(t)=WI(t)-[WR(t)+WT(t)]
(9)
式中:WI(t)为入射能,J;WT(t)透射能,J;WR(t)反射能,J;A为杆件横截面积,mm2;E为杆件材料的弹性模量,GPa;εI(t),εR(t),εT(t)分别为压杆上t时刻对应的入射波、反射波和透射波的应变。
为衡量在不同的入射杆冲击速度条件下,煤岩能量耗散的强弱,通常将耗散能与入射能的比值定义为能量耗散率N,计算如式(10)所示:
(10)
2 试验结果
2.1 典型试件电压时程曲线及应力平衡检验
试验时,电阻应变片采用平衡电压为4 V、增益500,半导体应变片采用平衡电压为2 V、增益100。典型电阻应变片与半导体应变片的测量电压时程曲线如图2所示。试验时,每组3个试件、共开展8组砂岩试件的冲击试验,分析时每组选择1个较好的数据进行分析,试验基本参数和数据处理结果见表1。
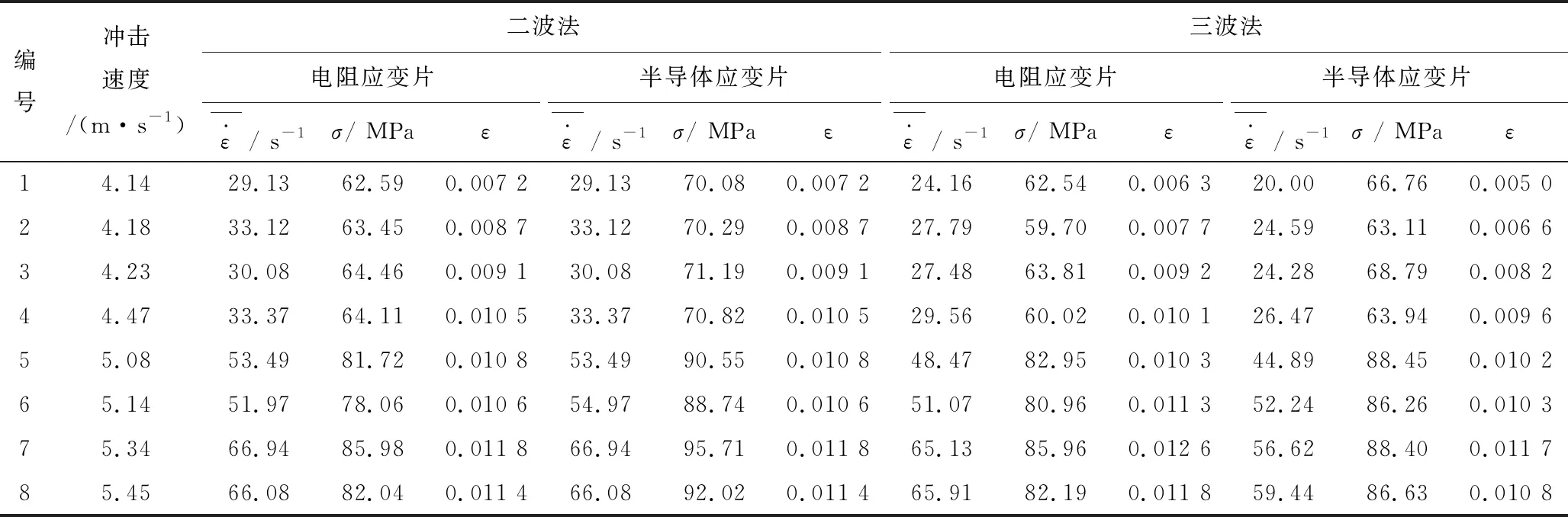
表1 砂岩试样动态力学参数
由图2可知,半导体应变片采集信号曲线幅值较电阻应变片大,采集的信号电压是电阻应变片的5倍左右,半导体应变片上升沿时间很短、能够较迅速地记录应力波变化的瞬时状态,表明采集的应力波数据更全面,不同冲击速度下,测试的入射、透射、反射电压均随着冲击速度增大,根据试验时导线接线情况,实测电压曲线中应力正值为压应力、负值为拉应力。
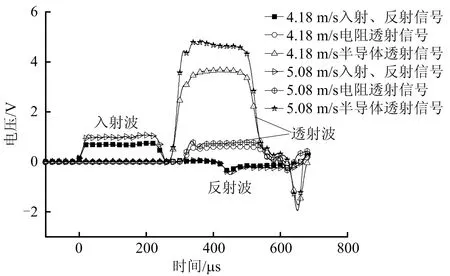
图2 典型试件电压时程曲线
为保证试验数据的有效性,进行应力均匀性假定验证,试件两端应力平衡检验如图3所示。
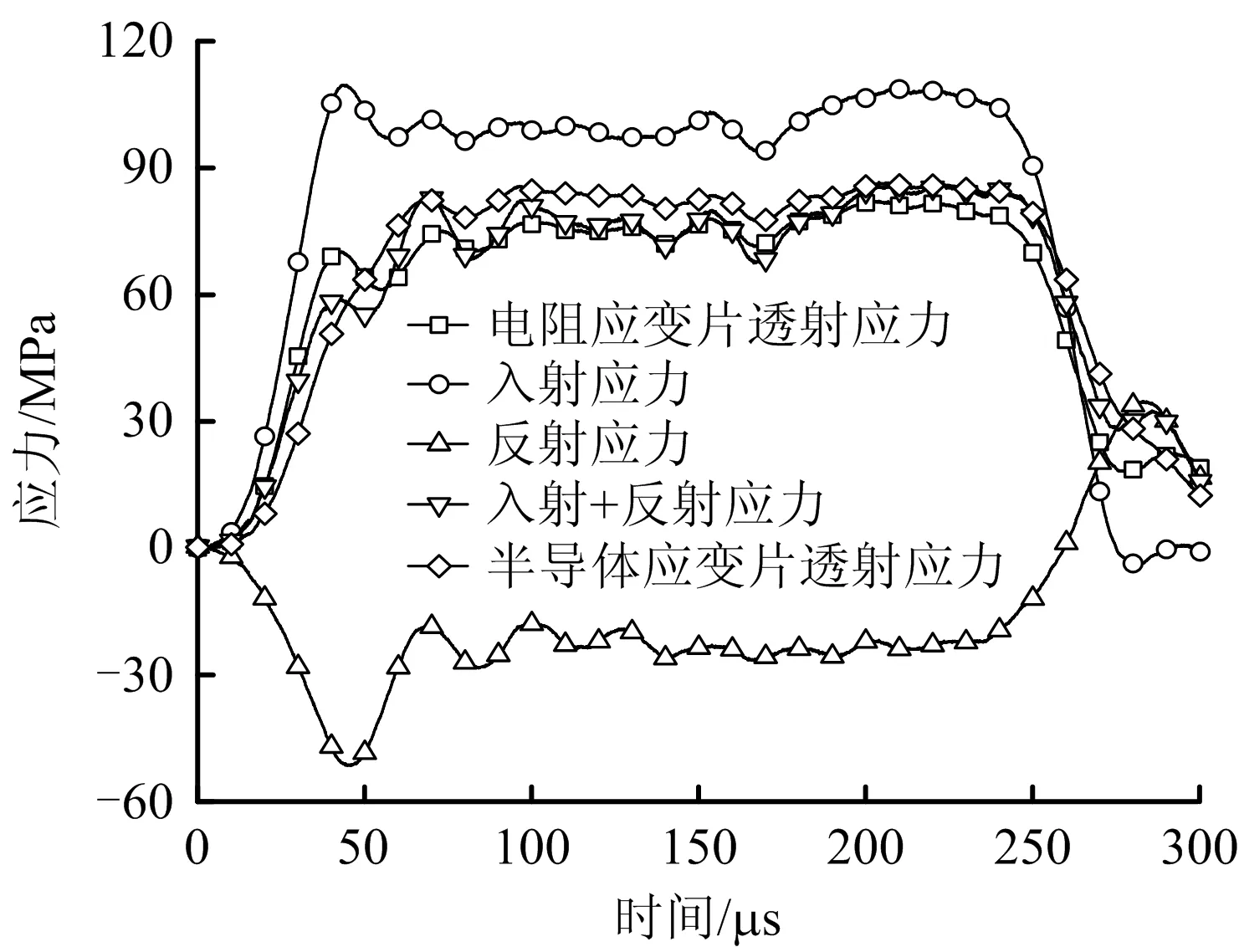
图3 试样两端的应力平衡检验
由图3可知,电阻应变片与半导体应变片所测透射应力与入射+反射应力具有较好的重合性,说明试件两端受力较均匀。对于冲击初始阶段,透射应力、反射应力的幅值均随着入射应力的增加而增加;当达到各自峰值应力时,电阻应变片所测数据均有一段减小的趋势后恢复,数据变化趋于稳定,半导体应变片所测数据则持续上升,后趋于稳定;半导体应变片所测平台值略高于电阻应变片。
2.2 试验数据处理
将应变片测得的电压信号转化为应变可求出应变率、峰值应变和动态压缩强度。计算结果存在以下关系:
1)试件应变率的求解只与反射波相关,则电阻应变片和半导体应变片测试结果采用二波法计算,得到的加载应变率与极限应变相同。
2)简化三波法采用三波法的公式对加载应变率与峰值应变求解、采用二波法公式对试件动态强度求解,所以简化三波法与三波法计算求得的加载应变率与极限应变相同,二波法与简化三波法计算求得的砂岩动态峰值强度相同。
为便于描述,定义电阻应变片用R表示,半导体应变片用S表示,用1,2,3分别表示二波法、简化三波法、三波法处理试验数据结果。则R2与R3,S2与S3求得试件加载应变率与极限应变相同,R1与R2,S1与S2求得砂岩动态峰值强度相同。因此,可不对简化三波法计算结果进行对比分析。
2.3 试件的动态力学参数
冲击荷载作用下,试件的动态力学参数主要有动态抗压强度、应变率和峰值应变,砂岩试样动态力学参数计算结果见表1。
3 试验结果分析
3.1 试件动态力学参数分析
1)应力应变曲线
2种应变片的测试结果处理得到动态应力应变曲线如图4所示。
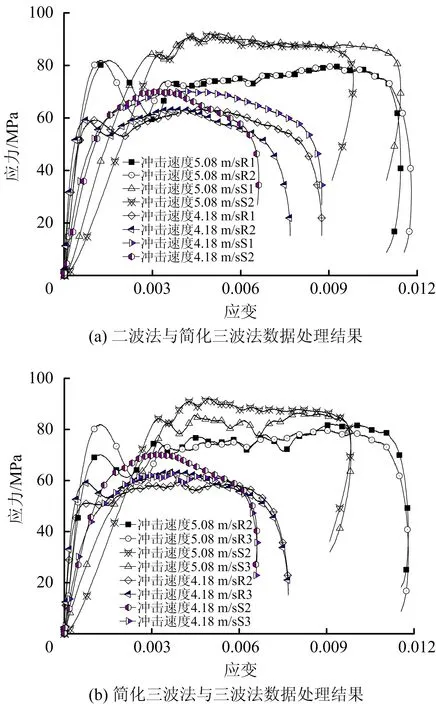
图4 应变片数据处理结果比较
由图4可知,二波法、简化三波法和三波法对2种应变片所测数据处理得到的试件应力-应变曲线具有如下规律:
①试件应力-应变曲线可分为弹性阶段、塑性阶段和破坏阶段。弹性阶段,应力应变关系呈线性,与电阻应变片相比,半导体应变片弹性阶段应力增长曲线斜率低,达到弹性阶段动态峰值强度对应的应变值也有所滞后;塑性阶段应力-应变曲进入加载平台阶段,应力增加平缓,半导体应变片所测数据较平滑;破坏阶段,超过岩石的动态屈服强度峰值,岩石裂纹不断发展,发生破碎破裂后,应力值迅速衰减。
②冲击速度大于5 m/s时试件弹性阶段变形和塑性变形和动态强度明显大于4 m/s时的作用效果,表明岩石的动态特性与冲击速度密切相关。由图4(a)可知,二波法处理结果动态强度峰值与简化三波法相同,在达到动态峰值强度之前,近似重合,达到峰值以后,半导体二波法应力衰减位置较简化三波法靠后。由图4(b)可知,简化三波法与三波法的应变峰值相同,采用电阻应变片,二者所求应力近似,半导体应变片简化三波法所测应力值偏大。
可见,半导体应变片与电阻应变片采集数据处理后可组合使用,相比电阻应变片,半导体应变片测量结果具有应力值高、峰值应变小、应力应变曲线光滑的特点。对于脆性材料,其动态强度高、变形小[19],而半导体应变片灵敏度高,测量应变灵敏性较高,且半导应变片所测应变峰值较小,动态强度较大,其应力-应变曲线对于描述脆性材料更加适用;图2的电压时程曲线也表明半导体应变片测试技术的可行性与优越性。
2)应变率分析
针对采用二波法、简化三波法和三波法处理半导体及电阻应变片所测砂岩试件,其应变率与冲击速度的关系如图5所示。
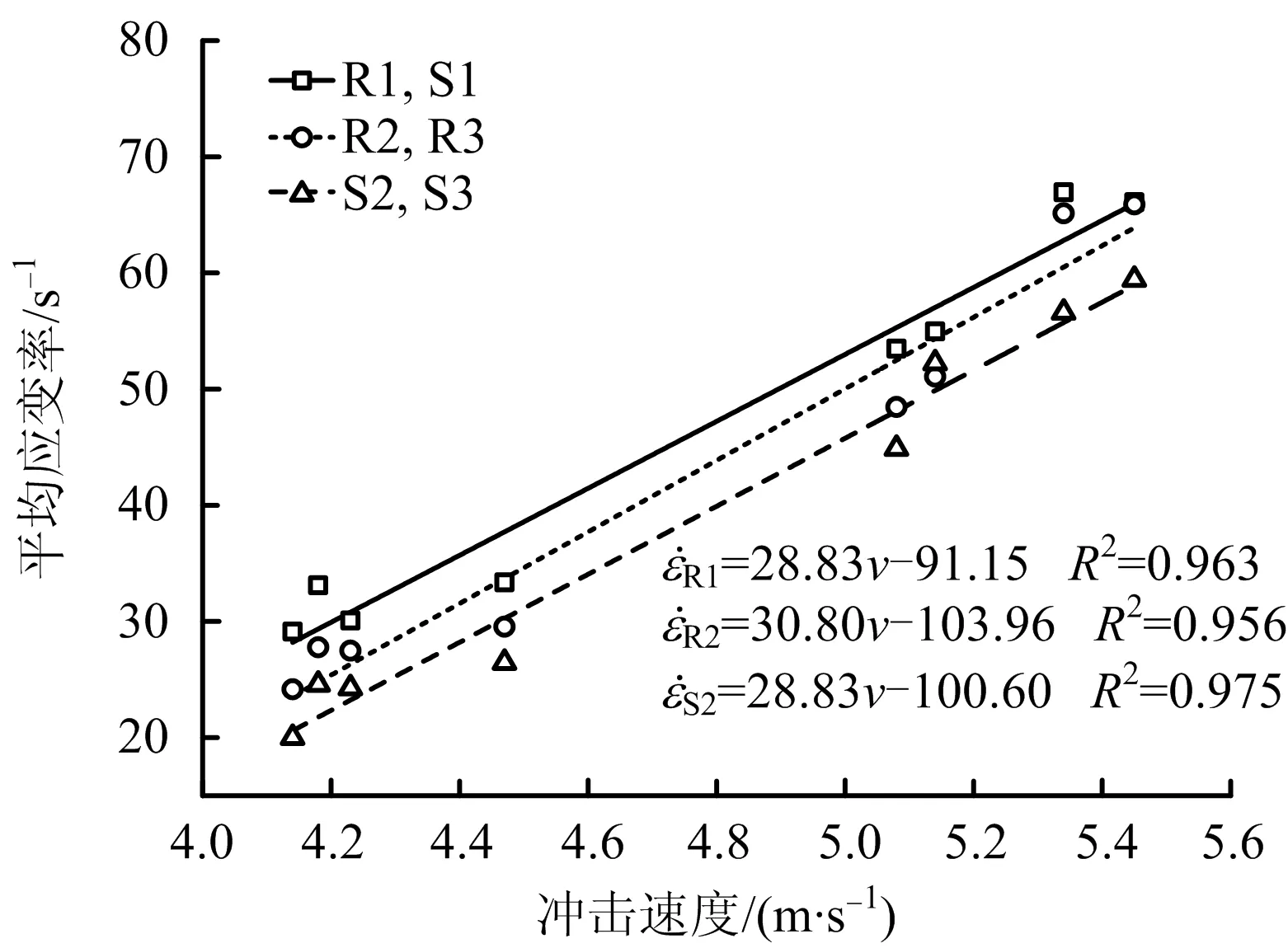
图5 试件应变率对比
材料的应变率与应变片所测应力波形密切相关,尤其与反射波形关系密切,在材料相同的情况下,反射应力波的变化主要受入射杆冲击速度的影响,即应变率与入射杆的冲击速度密切相关。图5中试件所受应变率随冲击速度增大而增大,S2,S3求解应变率值最小,R1,S1求解试件应变率值最大。这是因为砂岩的波阻抗与杆件的波阻抗相差4.33倍,反射系数为0.6,在入射波穿入砂岩试件的瞬时,会产生较大的反射波,采用二波法处理数据时应变率较高;对于同一试件,半导体应变片三波法处理砂岩应变率比电阻应变片低,对照应变率公式可知,试件入射波、反射波相同,透射应力波为主要影响因素,由于半导体应变灵敏系数高,记录的透射应力比电阻应变片高,致使应变率偏低,但不管采用哪种方法处理试验数据,得到的砂岩试件应变率与冲击速度关系符合图5中拟合关系式,具有较好正比关系,S2,S3求解得到砂岩应变率线性拟合相关系数最高。
3)应力分析
采用二波法、简化三波法和三波法处理得到砂岩的动态抗压强度与冲击速度关系如图6所示。
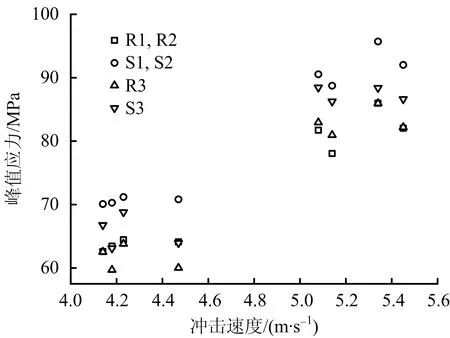
图6 试件动态强度对比
2种应变片采用二波法、三波法的计算结果趋势相似,S1,S2求得应力值最大,S3求解应力值大于电阻应变片;电阻应变片三波法与二波求解试件动态强度值结果相近。随着冲击速度的增加,试件动态强度整体呈上升趋势,这是因为冲击速度增加,应力波作用增强,在软岩内部缺陷被隐藏,即产生的裂纹尚未沿缺陷充分发展,便产生新的裂纹,从而引起试件整体动强度提高。
4)应变峰值分析
试件峰值应变对比关系如图7所示。
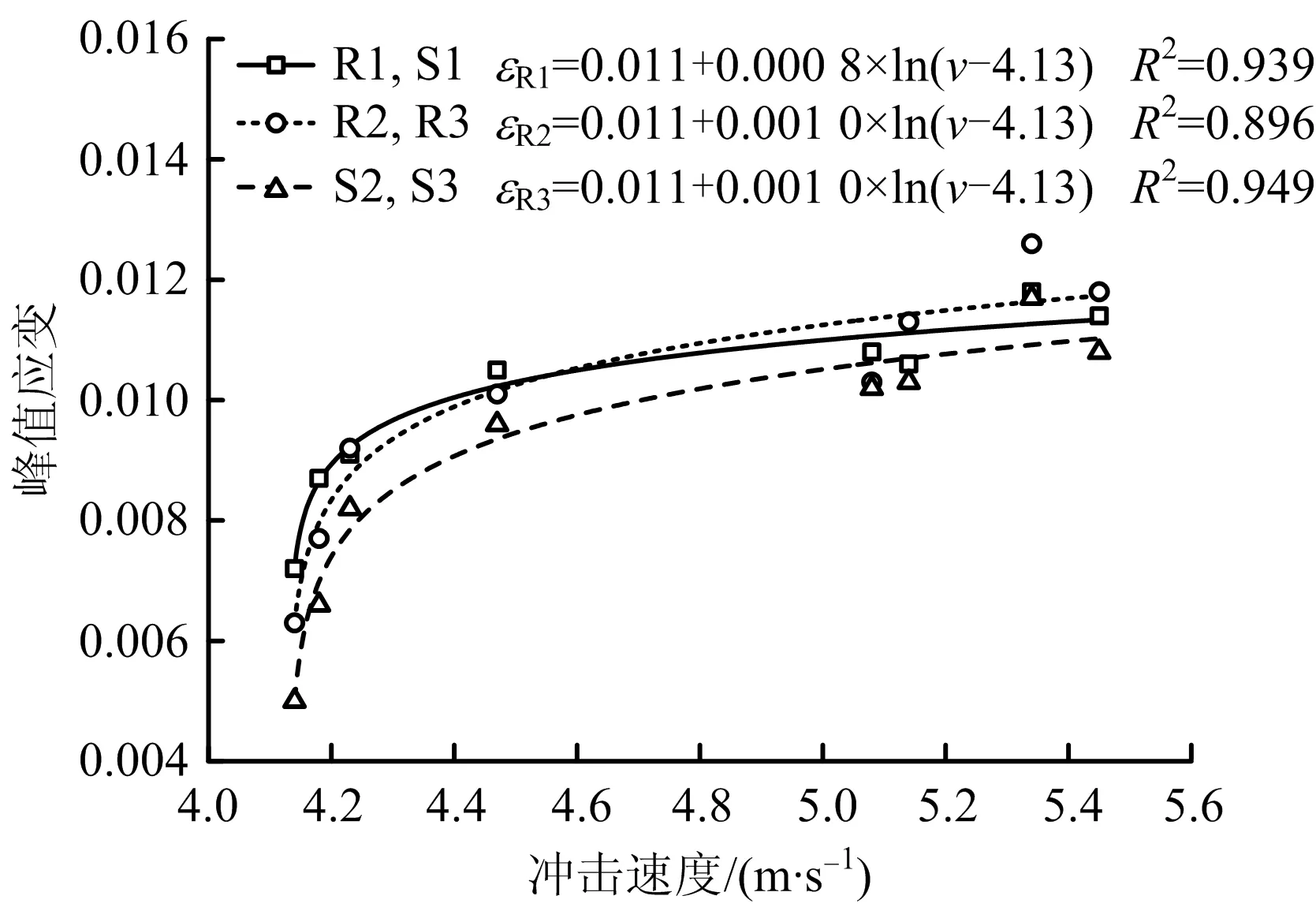
图7 试件峰值应变对比
由图7中拟合关系式可知,试件所受应变峰值随着冲击速度的增加而增加,半导体应变片测量应变峰值随冲击速度的拟合相关系数最高,当冲击速度超过某临界速度时,试件的峰值应变趋于定值,结合图7,发现半导体应变片三波法求解得到砂岩应变峰值最小,当冲击速度较小,电阻应变片三波法求解试件应变峰小于二波法,当冲击速度较大时,试件应变峰大于二波法,这是因为随着冲击速度的增加,应力波作用增强,半导体应变片的动态响应也更加敏感,相比之下,半导体应变片三波法求解试件应变更可靠。
3.2 试件破碎耗能分析
由于试验时只有透射杆上分别粘贴电阻应变片与半导体应变片,入射能和反射能由入射杆中电阻应变片测得,透射能由2种应变片分别表述,得到具体各类能量组成,见表2。
从表2中可以看出,半导体应变片所测砂岩试件透射能高于电阻应变片,高出值为0.8~9.63 J,将2种应变片测试结果计算得到的能量耗散率的差值称为能量耗散能误差,二者耗散率误差在10%以内,同时,2种应变片所测砂岩透射能随冲击速度变化规律具有一致的规律性,可相互验证。

表2 砂岩动态冲击能量计算结果
4 结论
1)半导体应变片因具有比电阻应变片更高的应变片灵敏系数,相比电阻应变片,测量结果具有应力值高、峰值应变小,应力应变曲线光滑的特点。
2)采用二波法、三波法和简化三波法处理电阻应变片与半导体片应变测量数据,处理结果规律具有较好的一致性;半导体应变片二波法求得的应力值比电阻应变片的应力值大10.44%~13.68%;三波法时半导体应变片半导体应变片求得的应力值相差2.84%~7.8%;三波法时半导体应变片求解得到的应变率和应变峰值略小于电阻应变片。综合对比,对于该测试系统建议采用三波法处理实验数据。
3)半导体应变片与电阻应变片所测能量随冲击速度变化规律具有一致的规律性,且耗散率误差在10%以内。

