带地形的ZTEM倾子资料三维正反演研究

李志强，孙洋，谭捍东，张承客

(1.江西省交通科学研究院，江西 南昌 330200； 2.中国地质大学(北京) 地球物理与信息技术学院，北京 100083)

0 引言

Z轴倾子电磁法(Z-axis tipper electromagnetic，ZTEM)是将天然场勘探深度大和航空测量工作效率高的特点有效地结合起来，基于音频磁场法AFMAG[1-2]发展而来的一种新型频率域航空电磁法[3]。该方法利用航空测量与地面基站观测的野外勘探方式，接收天然场源下25～720 Hz频段的磁场数据，并通过倾子T[4]建立磁场之间的联系，可以快速获得起伏地形下三维电导率构造信息。相比人工源航空电磁法，ZTEM具有勘探深度大、经济、高效等优点。

由于ZTEM是近年来才提出的一种航空电磁法，目前国外一些学者在从事这种方法的二维与三维正反演研究，并且应用到实例当中检验算法的有效性，目的是想利用频率域航空电磁法探测深部的地质构造和矿体，并且已取得较为丰富的成果[5-8]，实践应用表明ZTEM方法是实现经济快速探矿的理想手段。国内方面，王涛等[9]为探索该方法的参数响应特征，采用有限差分算法进行了ZTEM三维正演研究，为ZTEM的反演研究奠定了较好的基础。赵丛等[10]对比介绍了ZTEM方法和MT方法的特点，并提出利用这两种天然场源电磁法进行点面结合的联合深部矿产资源勘探思路。李志强等[11]采用三维数据空间OCCAM算法进行了ZTEM倾子资料的合成算例反演研究，并且与MT阻抗反演结果对比检验了算法的有效性，同时表明ZTEM参数反演的横向约束能力突出。而针对ZTEM空心感应磁传感器的感应线圈具有源阻抗大的特点，王言章等[12]对ZTEM磁传感器调理电路做了低噪声优化设计。此外，许智博等[13]基于有限差分正演还实现了二维ZTEM非线性共轭梯度(NLCG)反演算法。

考虑地形因素的影响，国外学者Sasaki等[14]证明了ZTEM三维反演时地形效应在较高频时更显著的特点，Legault等[15]和Sattel等[16]分别对比分析了起伏地形下二维、三维ZTEM和MT单独与联合反演的效果，说明了联合反演中可利用MT反演结果来校正ZTEM反演时的背景电阻率，而三维联合反演更能真实恢复出地下电导率结构。当前国内研究地形对航空电磁的影响主要集中在主动源的正反演数值模拟中，张博等[17]应用非结构网格矢量有限元法模拟分析了起伏地表下的三维频域/时域航空电磁响应特征，为航空电磁地形效应的有效识别提供了可能；王卫平等[18]采用有限差分法分析了频率域航空电磁法的地形影响，并采用地形校正方法对典型地形地电模型进行了校正，提高了异常响应特征的解释效果；李文奔[19]开发实现了起伏地表下的频率域二维航空电磁高斯-牛顿反演算法，通过模型算例表明忽略地形反演会造成虚假异常的产生。国内学者为了适应地形起伏的实际情况，也对天然场源的大地电磁法(MT)进行了带地形的二维、三维正反演研究[20-21]。鉴于航空电磁法在起伏地形区域的勘探优势明显，而实际野外探测作业中地形的变化影响又不容忽视，本文基于ZTEM三维数据空间OCCAM反演算法[11]，主要研究了带地形的ZTEM倾子数据三维正反演算法，通过合成算例计算和分析纯地形的ZTEM三维响应(倾子)特征，对典型地电模型ZTEM带地形与不带地形的反演算例进行了探讨分析，检验了带地形的ZTEM数据空间OCCAM反演算法的有效性与可靠性。

1 起伏地形下ZTEM三维正演

1.1 倾子资料整理

ZTEM方法的倾子数据是将地面以上空气层中不同位置处r的航空测量垂直磁场与地表某一固定参考基站处r0的两个水平磁场联系起来[11]，其关系表示如下：

Hz(r)=Tzx(r,r0)Hx(r0)+Tzy(r,r0)Hy(r0),

(1)

式中：Tzx和Tzy表示倾子分量。

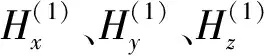
(2)

解方程(2)即可得到倾子T的关系式：

(3)

1.2 倾子响应的计算

在音频段的ZTEM勘探方法中，位移电流可忽略，假定地下介质磁导率近似为自由空间中的磁导率μ0，时谐因子取为e-iωt，则ZTEM方法电强度E和磁场强度H所满足的Maxwell方程组的微分关系式可表示为

(4)

(5)

式中：ω是角频率，μ0是磁导率(真空中)，σ是电导率。

KE=S,

(6)

式中：K为矩阵元素与网格单元电阻率及尺寸有关的对称大型稀疏系数矩阵；E表示需要求解的电场三分量列向量；S为列向量，与场源及边界值有关。在场源SX极化模式下，方程左端的电场值记为E(1)，右端列向量记为S(1)；在SY极化模式下，方程左端的电场值记为E(2)，右端列向量记为S(2)，则式(6)可分解为两个正演方程：

KE(1)=S(1),KE(2)=S(2)。

(7)

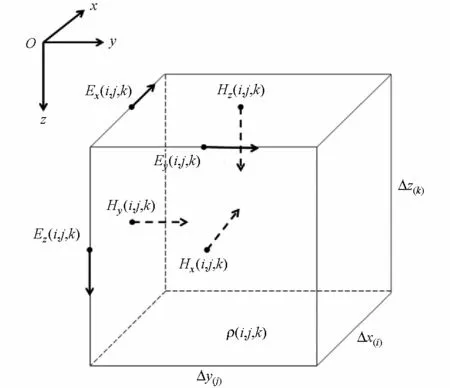
图1 编号为(i，j，k)的网格单元Fig.1 The (i，j，k) grid cell

研究区域的电场值E(1)和E(2)就通过QMR法求解这两个正演方程得到。

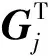
(8)

式中：hG表示区分有两个对应两种极化方式下磁场与电场转化关系式G向量,h=1或2。正演模拟时，对于起伏地表水平磁场观测基站所处单元为(i0,j0,ki0,j0)上表面中心处Hj的两个分量Hjx、Hjy,对应方程(8)的关系式[25-26]分别为：

(9a)

(9b)

空气层中某网格单元在(i,j,kair)面中心上的垂直磁场Hjz可表示为：

(Ey(i+1,j,kair)-Ey(i,j,kair))/Δx(i)]。

(9c)

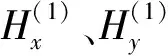
1.3 正演精度的验证

选取二维四棱台状山峰纯地形模型来试算，以此验证带地形的正演计算结果的准确性。如图2所示，走向为x方向，四棱台状山峰在yz方向上顶面距地表高160 m，上顶边长800 m，下底边长3 200 m，地下介质与空气层电阻率分别设为100 Ω·m和108Ω·m。选取(10 100 m，0 m)地表固定点作为两个水平磁场分量取值位置，垂直磁场的取值高度设置在离四棱台状山峰顶面高100 m的空气层中。

用上述带地形的三维有限差分正演算法计算出纯地形模型的数值解，将其结果与二维有限差分法计算得到的倾子响应进行对比，图3a、b表示两种数值模拟算法当频率在25 Hz与200 Hz时ZTEM异常响应Tzy分量的实、虚部对比结果，其中“▽”和“○”分别表示频率在25 Hz和200 Hz时的三维数值解，“*”和“×”分别表示频率在25 Hz和200 Hz时的二维数值解。图3中二维与三维数值解对比反映出倾子响应的实、虚部都能较好的吻合，证明了所开发的ZTEM带地形的三维正演算法准确可靠。

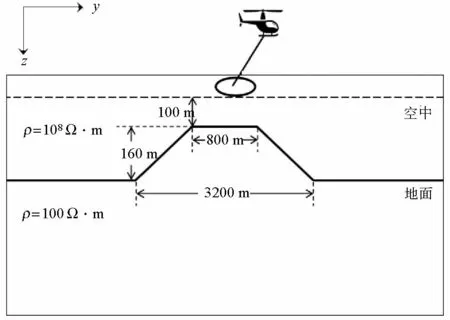
图2 ZTEM正演模型Fig.2 The model of ZTEM Forward modeling

2 三维反演算法

本文带地形的反演算法是基于ZTEM三维数据空间OCCAM反演代码的基础上所实现的，实际反演问题中，假定观测数据总个数为N，模型单元总个数为M，将目标函数[26]定义为：

(10)

式中:m为待更新的电阻率模型，m0为带地形的初始模型，Cm和Cd分别是模型协方差矩阵和数据协方差矩阵，λ-1表示拉格朗日乘子，d表示观测数据，F[m]是带地形的模型响应，X*为期望拟合差水平。

对于第k+1次迭代，将模型空间OCCAM的迭代公式[22]作以下数学变换：

(11)

(12)

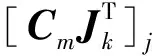
图3 二维山峰纯地形模型倾子响应的二维、三维计算结果对比Fig.3 The tipper response comparison between the 2D finite difference modeling results and the 3D finite difference modeling results generated from 2D peak terrain model

带地形的ZTEM数据空间OCCAM反演问题中，为实现模型的更新迭代，需要通过计算得到的雅克比矩阵Jk获得每次模型更新所需的模型修正量，而最为关键的是计算正演响应F和求解对应的Jk。倾子用于反演的第k个模型参数的偏导数Jk=(∂F/∂m)k可相应表示为Jk=(∂T/∂m)k[10]，将式(3)对模型电导率参数σk求偏导数，有:

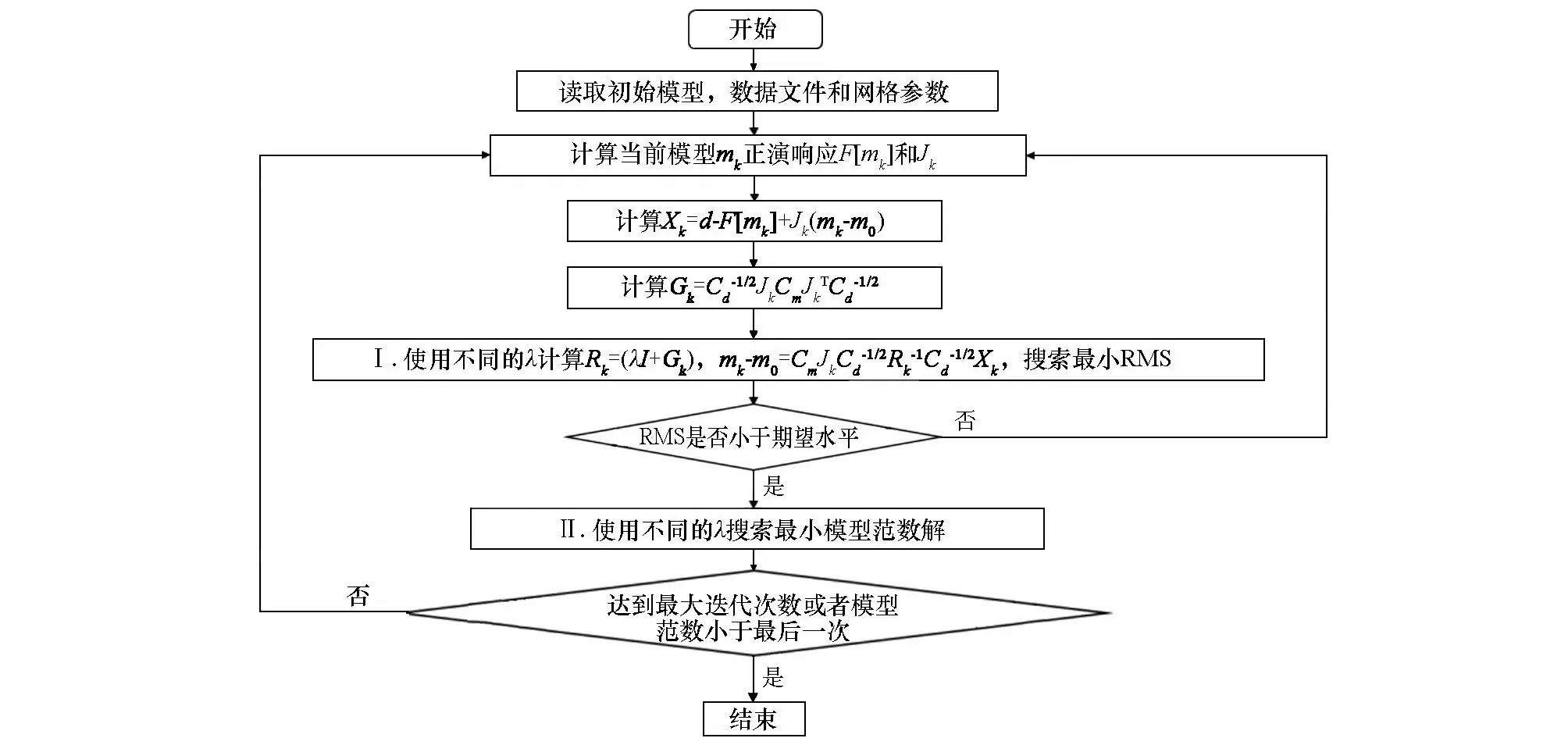
图4 数据空间OCCAM反演流程Fig.4 The flow chart of data-space OCCAM inversion

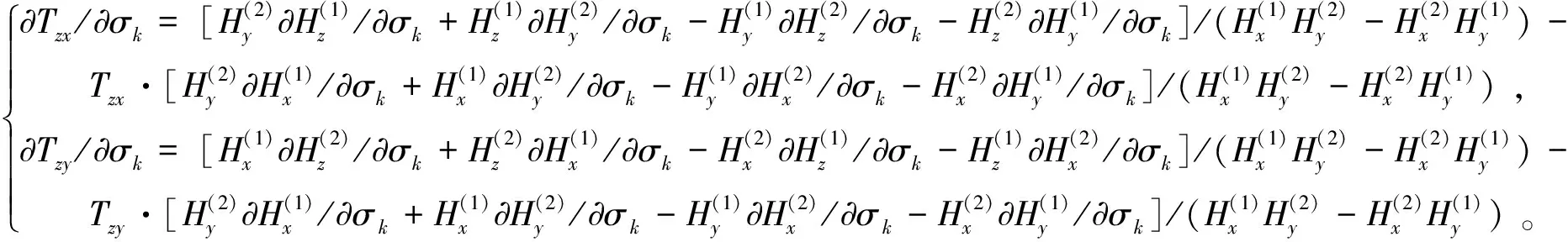
(13)

由于正演模拟采用的是电场方程，首先将电场正演方程(6)KE=S对模型电导率σk求偏导，考虑S与σk之间的弱相关性，可以将∂S/∂σk略去，有

∂E/∂σk=K-1(-∂K/∂σkE)。

(14)

(15)

接着将关系式(15)代入式(13)，则第k个模型电导率参数σk的扰动对第j个测点的改变量∂Tzxj/∂σk与∂Tzyj/∂σk就写成如下形式：

式中：

(16)

在ZTEM正演中，差分系数对称矩阵K满足(K-1)T=K-1，故上式中∂Tzxj/∂σk和∂Tzyj/∂σk可写成:

∂Tzxj/∂σk=(-∂K/∂σkE1)TK-1(1Gjzx)+

(-∂K/∂σkE2)TK-1(2Gjzx),

(17)

∂Tzyj/∂σk=(-∂K/∂σkE1)TK-1(1Gjzy)+

(-∂K/∂σkE2)TK-1(2Gjzy)。

(18)

从式(17)、(18)可看出，先把1Gjzx、2Gjzx计算出后再求解

K·v1=1Gjzx,

(19)

K·v2=2Gjzx,

(20)

可得到向量v1=K-1(1Gjzx)和向量v2=K-1(2Gjzx)，同时解两次正演方程获得电场值E(1)、E(2)后代回式(17)，即可求得某个测点位置的倾子分量Tzx的偏导数∂Tzxj/∂σk。同样方法可以计算求出∂Tzyj/∂σk。

3 合成算例分析

3.1 三维纯地形的异常特征

设计一个正四棱台状的山峰地形来分析其ZTEM正演倾子平面响应特征。如图5所示，棱台状山峰的顶面相对于地面有0.45 km，上顶面边长有0.5 km，下底边长有2.5 km，空气层电阻率为108Ω·m， 地下介质的电阻率为100 Ω·m， 选取地表固定点(5 750 m，5 750 m，0 m)作为两个水平磁场分量取值位置，垂直磁场的取值高度设置在离山峰高100 m处。x、y、z方向网格单元剖分数分别为31、31、31(包含空气层数为14)。

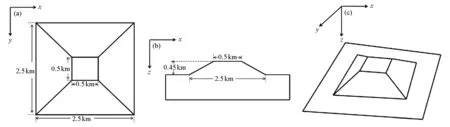
图5 山峰地形模型在xy方向的模型视图(a)、xz方向的模型视图(b)及xyz方向的模型视图(c)Fig.5 Schematic diagram of peak terrain model in the view in xy direction(a), in the view in xz direction, and the view in xyzdirection

图6展示了频率为50 Hz山峰纯地形的ZTEM三维倾子响应，图中白色实线表示山峰下底边界。由图不难发现，在山峰地形的下底边界位置(即地形突变的位置)处都会产生反映x、y方向边界信息的正负极值虚假异常区域，Tzx的实、虚部在x方向上有对称异常，实部和虚部正负异常出现相反的特征，这与山峰地形在横向上空气与地下介质的边界特征是相匹配的，与此同时，Tzy在y方向出现类似特征。因此，在进行反演数值模拟时，需要考虑到地形因素产生的虚假异常对反演结果所产生的影响。

合成山谷纯地形的算例进行对比分析，其上顶面边长为2.5 km，下底边长为0.5 km，下底面低于地面0.45 km，其他计算条件及参数信息与山峰地形一致。如图7所示，在地形突变的位置，出现了与山峰地形相反的ZTEM倾子平面响应特征，此时Tzx和Tzy的实虚部的虚假异常区域要比山峰地形的更大，异常的极值也略大于山峰地形的虚假异常，这些虚假异常在起伏地形下的反演工作不可忽略。

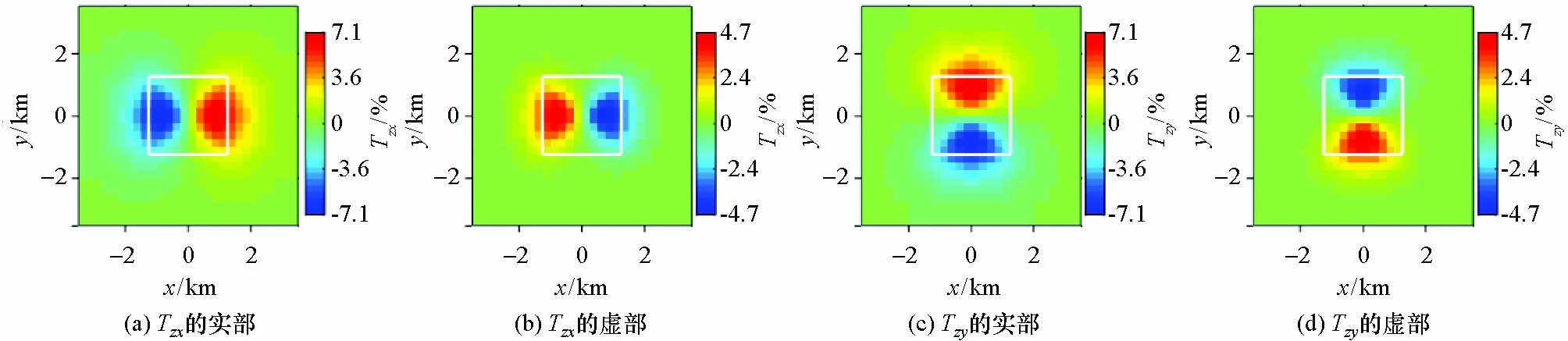
图6 频率在50 Hz时山峰模型的ZTEM响应Tzx和Tzy平面分布(白色框为模型的轮廓)Fig.6 Contour of the ZTEM tipper response Tzx & Tzy at 50 Hz generated from 3D in peak terrain model(the white box is the outline of the model)

图7 频率在50 Hz时山谷模型的ZTEM响应Tzx和Tzy平面分布(白色框为模型的轮廓)Fig.7 Contour of the ZTEM tipper response Tzx & Tzy at 50 Hz generated from 3D in valley terrain model(the white box is the outline of the model)

3.2 反演算例分析

为了探讨地形因素对反演结果可能造成的影响，分别设计一个山峰和山谷地形条件下的低阻单棱柱体模型进行试算，从而进一步说明所开发ZTEM反演代码对带地形条件下的地电模型反演的有效性和稳定性。

模型一：图8所示的是一个山峰地形条件下低阻棱柱体的反演算例，在山峰下方离水平参考地面0.2 km处有一个x×y×z为1 km×1 km×0.3 km的单棱柱体，其电阻率为100 Ω·m，地下介质的电阻率为500 Ω·m，空气层电阻率为108Ω·m。将研究区域离散化，目标体中心区域x、y、z方向分别用250 m×250 m×100 m的网格进行均匀剖分，由于远参考基站位置距离目标体研究区域相对较远，因此，采取向外加大间距的方式进行网格剖分，x、y方向均设置为28个网格，z方向有30个网格(包含11层空气层)。

反演的初始模型为带地形的均匀介质空间，电阻率取500 Ω·m，使用频点个数有5个(25、100、200、400、500 Hz)，水平磁场取值位置在(5 100 m，5 100 m，0 m)的水平地表处，垂直磁场取在离山峰顶面高100 m所处平面上，对所示模型进行三维正演计算，模拟测点数有36个(图8中倒三角形所示位置)，对参与反演的倾子分量加入5%的随机误差，用于模拟实测资料。经过10次迭代后，历时9 h40 min， 反演结果如图9第一、第二行所示。

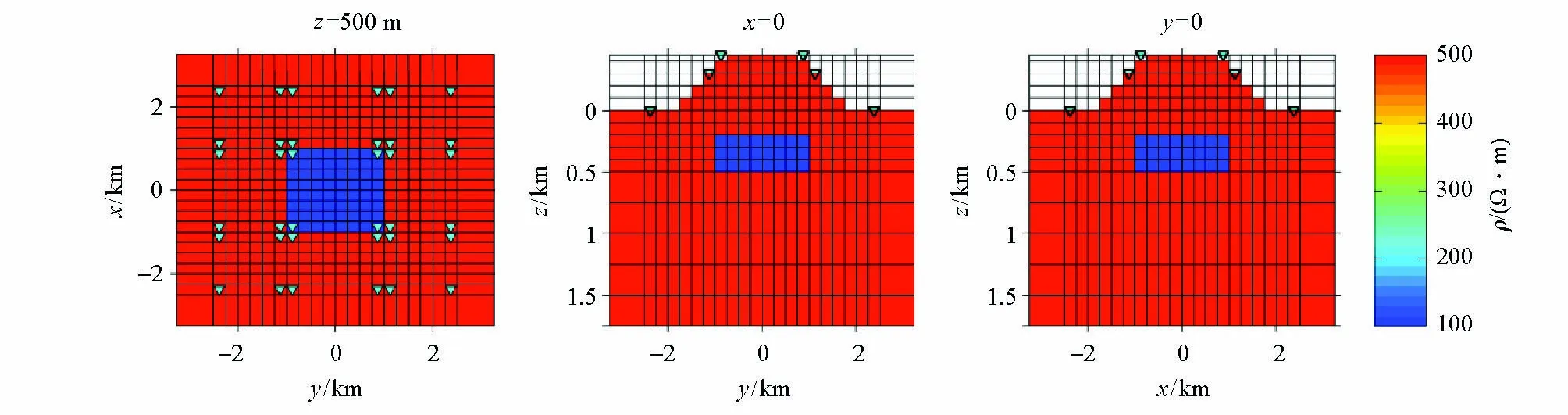
图8 低阻棱柱体模型示意(山峰地形)Fig.8 Schematic diagram of conductive prism model (peak terrain)

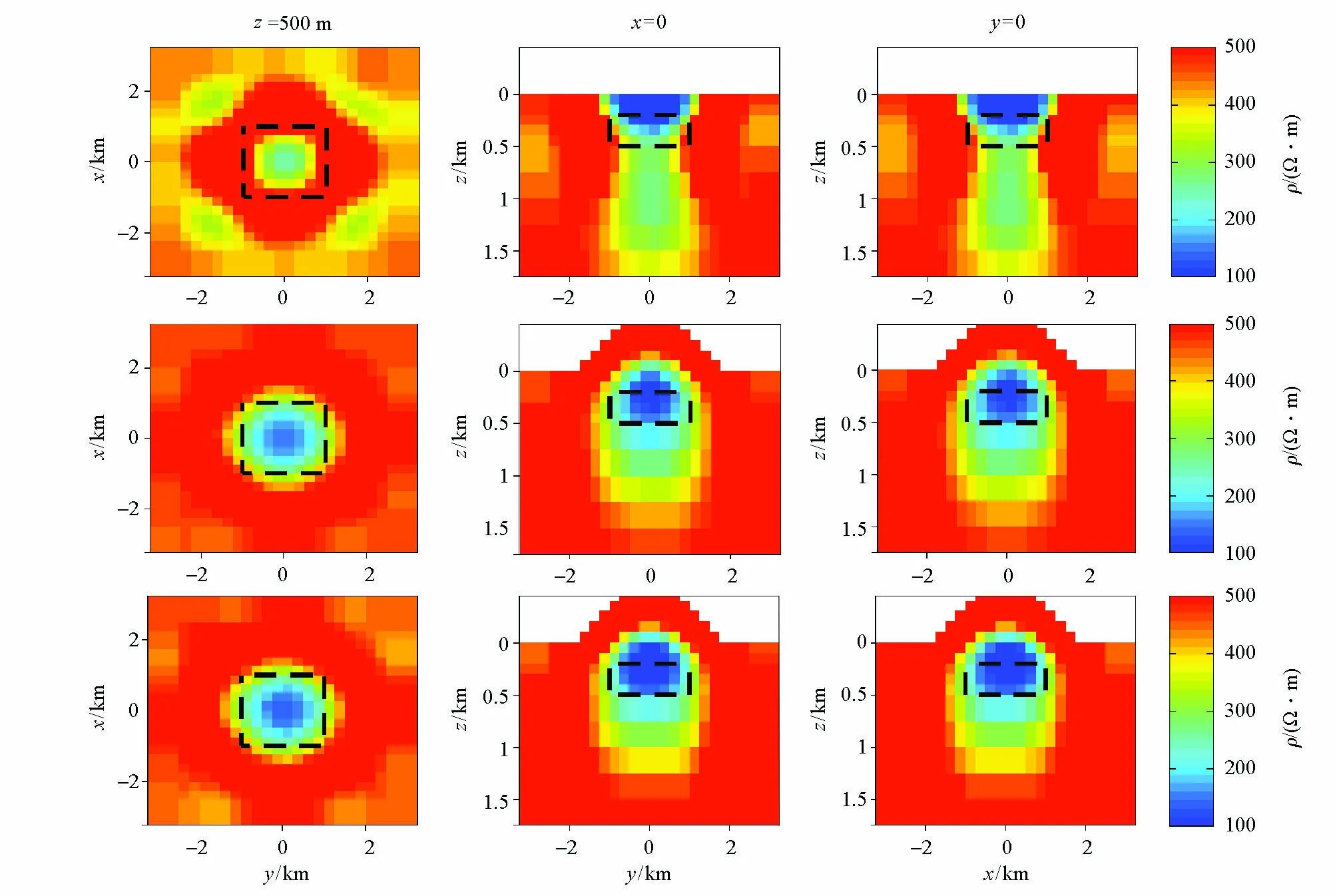
第一行—5个频率的水平地形ZTEM倾子反演结果；第二行—5个频率的带地形ZTEM倾子反演结果；第三行—8个频率的带地形ZTEM倾子反演结果；第一列—深为500 m的水平切片；第二列—x=0时沿y方向的垂直切片；第三列—y=0时沿x方向的垂直切片；黑色虚线—棱柱体的边界the top row—the results from the inversion of tipper data (ZTEM) with five frequencies；the second row—the results from the inversion of tipper data (ZTEM) including topography with five frequencies；the third row—the results from the inversion of tipper data (ZTEM) including topography with eight frequencies；the first column—the horizontal slices at 500 m depth；the second column—the vertical slices at y=0 m along the y axis；the third column—the vertical slices at y=0 m along the x axis；the black dashed lines—the prism margins图9 低阻体模型ZTEM倾子响应数据不带地形与带地形的三维反演结果(山峰地形条件)Fig.9 Results from the 3D inversion of tipper ZTEM data generated from 3D conductive prism model (peak terrain)

从反演结果图中可以发现，带地形的ZTEM三维反演基本恢复出了目标体的位置和形态，所恢复的模型在横向边界上具有较好的约束，纵向上存在拉伸的趋势，对纵向边界的恢复效果较差，说明ZTEM方法对纵向上的信息缺乏约束力。在山峰地形的影响下，由于在地形突变位置处存在虚假异常，因此实际恢复出的目标体电阻率偏大(最小为114.7 Ω·m)。对于不带地形的ZTEM三维反演，虽然基本恢复出了目标体的主要特征，但是其位置和形态发生了较大畸变，反演效果较差，且纵向上的拉伸趋势更为明显，目标体下方出现虚假异常，同时在地形起伏变化的位置附近产生了较为严重的虚假异常。

当把频点数增加至8个参与带地形的反演而其他反演条件不变时，反演结果如图9第三行所示，纵向上仍存在一定的拉伸，实际反演出的电阻率更接近目标体电阻率，可达到95.2 Ω·m，对反演结果有一定的改善。

模型二：山谷地形条件下，距离地表0.65 km处有一个1 km×1 km×0.3 km的低阻单棱柱体，山谷底边界距离地表有0.45 km，上顶边长有2.5 km，如图10所示，其他计算条件与山峰地形条件下的低阻单棱柱体一致。

经过10次迭代，历时12 h33 min，ZTEM倾子数据带地形反演结果与不带地形的反演结果对比如图11所示。带地形ZTEM三维反演所恢复的反演模型较好反映出了目标体的形态与位置，尤其是对目标体的横向边界位置恢复效果更为理想，相比于山峰地形条件，其纵向上的拉伸趋势有所减弱，但对于上下底边界的约束同样存在不足，这是ZTEM方法本身所存在的一个缺陷。受山谷地形条件的影响，目标体所恢复出来的电阻率离真实电阻率还有一定差距(最小为142.2 Ω·m)，这与山谷地形类似为高阻体的特征相符。

对于不带地形的ZTEM三维反演模型,大致反演出了目标体的轮廓，但目标体形态和位置与正演模型相差较大，产生了较为严重的畸变，在目标体周围反演出了虚假异常体，并且在地形突变位置附近反演产生了部分虚假异常。

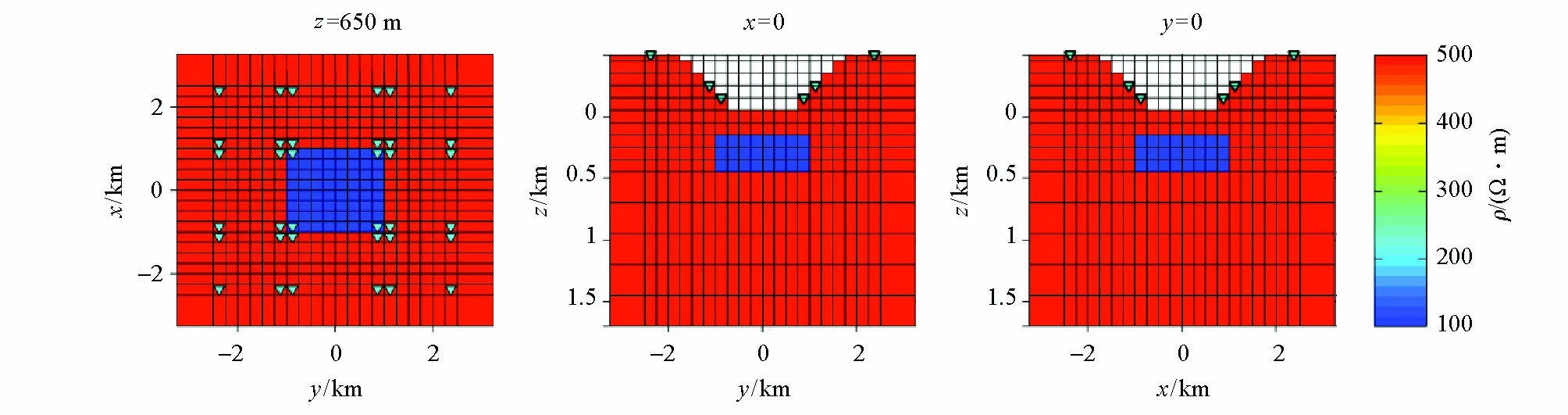
图10 低阻棱柱体模型示意(山谷地形条件)Fig.10 Schematic diagram of conductive prism model (valley terrain)

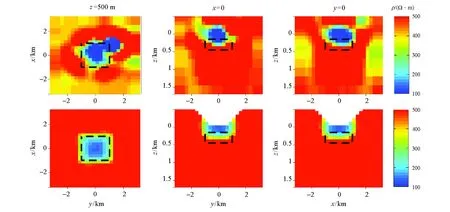
第一行—水平地形ZTEM倾子反演结果；第二行—带地形ZTEM倾子反演结果；第一列—深为650 m的水平切片；第二列—x=0时沿y方向的垂直切片；第三列—y=0时沿x方向的垂直切片；黑色虚线—棱柱体的边界the top row—the results from the inversion of tipper data (ZTEM)；the second row—shows the results from the inversion of tipper data (ZTEM) including topography；the first column—the horizontal slices at 650 m depth；the second column—the vertical slices at x=0 m along the y axis；the third column—the vertical slices at y=0 m along the x axis；the black dashed lines—the prism margins图11 低阻体模型ZTEM倾子响应数据不带地形与带地形的三维反演结果(山谷地形条件)Fig.11 Results from the 3D inversion of tipper(ZTEM) data generated from 3D conductive prism model (valley terrain)

4 结论

基于三维有限差分正演算法分析了纯起伏地形的ZTEM响应特征，在考虑地形因素的影响下，开发实现了带地形的三维ZTEM反演算法。合成算例分析表明，基于有限差分正演的带地形ZTEM数据空间OCCAM反演方法可以得到比较接近地下真实导电性结构的反演模型，说明了ZTEM带地形进行反演的算法准确有效，可以有效减少虚假异常的产生。

通过山峰和山谷地形下低阻棱柱体的带地形与不带地形的反演算例计算结果对比分析，表明地形因素会对模型的形态、位置和电阻率恢复值带来一定影响。水平地形的反演算法计算带地形的数据时会带来一些虚假异常，并使目标体的形态产生畸变，而带地形的三维ZTEM反演能够得到比较接近真实的反演目标体模型，可以有效减少虚假异常，尤其对模型横向上的边界具有较好的约束能力，但对垂向边界的恢复能力略显不足。此外，由于模拟起伏地形的需要，有限差分法需要在空气与地表界面处做精细剖分，不可避免地会增加模型网格数，从而导致出现反演时间增长等问题。后续研究需要进一步考虑采用并行算法来解决运行效率的问题。

致谢感谢审稿专家提出的宝贵修改意见和编辑部的大力支持！