基于TOPSIS价值函数的超级高铁特征综合评判

耿灿欣，宋 阳，吴翊恺

基于TOPSIS价值函数的超级高铁特征综合评判

耿灿欣，宋 阳，吴翊恺

（南京理工大学，自动化学院，南京 210094）

为了更加直观地观察超级高铁设想特征的优良等级，采用TOPSIS价值函数法对超级高铁的特征进行综合评判，并与模糊理论的评判过程与结果进行对比。首先，从“速度-安全性-舒适性-稳定性-经济性”的角度对影响超级高铁特征的因素进行分析，确立13个特征评判指标，建立超级高铁特征的评判指标体系；其次，运用熵值法计算得到13个评判指标的权重系数；然后，结合TOPSIS价值函数法和模糊综合评价法的适应性特点，分别对超级高铁的特征等级进行评判；最后，对两种评判方法进行对比分析，选取更适用于超级高铁特征评判的方法。评判结果表明，超级高铁特征等级为“良好”；两种方法相对而言，模糊综合评价法评价步骤较为简单，但评判过程中的主观性因素较多，TOPSIS价值函数法的评判过程更加直观、客观、严谨，评价结果更具有说服力。此结果直观地反映了超级高铁特征的优越性，表明TOPSIS价值函数法在超级高铁特征综合评判应用中有较好的实用性。

超级高铁；特征评判；TOPSIS价值函数；模糊综合评价法

0 引 言

超级高铁是一种以“真空管道运输”为理论核心而设计的交通工具[1, 2]。1904年美国学者罗伯特·戈达德提出了真空管道交通系统的设想[3]，在波士顿到纽约之间建立一条真空管道铁路线，让磁悬浮列车在其中运行。1974年，瑞士的鲁道夫·里斯提出地下真空隧道磁悬浮列车的概念[4]，并受到瑞士洛桑联邦理工学院专家的支持，于1992年成立了专门从事瑞士超高速地铁项目研发的Swissmetro SA公司。20世纪90年代美国机械工程师达里尔·奥斯特思考“真空管道运输”的可行性，并且在1999年为这一概念申请了真空管道运输系统的发明专利[5]，于2010年，奥斯特成立了致力于开发真空运输项目的公司ET3。2004年12月，西南交通大学召开了“真空管道高速交通”院士学术报告会，报告会对真空管道交通运输未来的发展及实用性、经济性等展开了讨论，拉开了中国学者研究真空管道运输系统的序幕。沈志云就管道压强、遮挡系数及其关键技术等基本问题，论述了我国发展真空管道高速交通的必要性和可行性[6]。2011年，在西南交通大学超导与新能源研究开发中心，一套完整的真空管道磁悬浮系统正式通过国家教育部专家组的验收，该系统可以模拟真空环境下的磁悬浮列车运行情况，真空管道磁悬浮列车的研究从理论进入到了试验阶段。自2010年起，美国相继成立了ET3、SpaceX、HTT等多家研发超级高铁的公司。2013年，美国电动汽车公司特斯拉CEO埃隆·马斯克对“真空运输”这一概念进行了丰富，发布了名为《超级高铁缘起》的白皮书[7]，介绍了他的超级高铁概念。2017年8月，中国航天科工公司在武汉宣布，已经启动时速为1 000km的“高速飞行列车”研发项目，后续还将借助航天系统工程丰富的实践经验和技术积累以及国际一流的超声速飞行器设计能力，研制最大运行时速为2 000 km和4 000 km的超级列车。

在大量学者投入超级高铁研究的同时，一些学者、公众也发出了质疑。例如，真空管道内外的压强差极大，现有的技术手段能否达到要求；超级高铁对各方面的要求极高，这就导致整套系统非常脆弱，哪怕一个点失败，都有可能引发严重事故；超级高铁在实际运行时，由于涉及跨国运输，不同国家的协同管理难以解决。因此，超级高铁的综合评判迫在眉睫。目前，超级高铁的特征评判体系还不完整，为了更好地了解超级高铁的特征，笔者将借鉴高速铁路的评价体系和评价方法，建立超级高铁的特征评判体系，运用TOPSIS价值函数法以及模糊综合评价法对其进行评价，为超级高铁的特征评价提供科学依据。

1 超级高铁特征评判指标体系

超级高铁的特征评判体系服务于运输企业和旅客，作为“第五种交通方式”的工具，影响超级高铁特征的因素多种多样，各子系统之间也会相互影响。超级高铁的特征评判指标体系的构建，应该遵循科学性、全面性、系统性、典型性、综合性等原则。依据上述指标选取原则，对超级高铁的特征进行分类统计解析，建立超级高铁特征评判指标体系，包括目标层、准则层、指标层。

对超级高铁的特征评判指标要符合一般交通运输工具的评价原则，并在评判过程中具有一定的代表性。首先，速度作为交通工具的本质属性，人类对它的追求从未停止，在超级高铁的特征评判体系中也要对速度进行评价；其次，无论哪种交通工具，安全都是首要的，出行的安全可靠是旅客考虑的重要因素，张耀平等[8]分析了真空管道运输安全问题的成因，在此基础上，笔者将超级高铁的安全性作为其评判指标进行评价，包括自然灾害、人为失误、脱轨等因素对超级高铁安全性的影响；再次，在确保安全的同时，舒适性也是评判交通工具特征优良等级的因素，同时也是出行者选择出行方式的重要因素，超级高铁的舒适性评价包括车内环境、座椅舒适性以及噪声影响；然后，交通工具系统的稳定性决定了其运行的连续性以及可靠性，任何系统的不稳定都会导致行程中断甚至发生交通事故，超级高铁稳定性的评价包括电力系统稳定性、推进系统稳定性以及控制系统稳定性；最后，经济性是建设超级高铁需要考虑的条件之一，也是出行者选择交通工具的因素，张耀平[9]研究了管道断面尺寸对真空管道交通建设成本与运营成本的影响，提出管道断面尺寸是影响真空管道建设成本和运营成本的主要因素，笔者从建设成本、运营成本和维修成本三个方面对超级高铁的经济性进行评判。超级高铁特征评判指标体系如图1所示。

图1 超级高铁特征评判指标体系

2 基于不同方法的超级高铁特征综合评判

目前在交通领域的综合评价有很多不同的方法，主要包括层次分析法、模糊综合评价法、灰色关联系数法和价值函数法等。王迎晗等人运用网络层次分析法（ANP）和模糊综合评判相结合的模糊网络分析法（F-ANP）建立高速铁路运营安全评价模型[10]，对高速铁路运营安全情况进行了评价；郑丽媛等人运用模糊综合评价法、灰色度关联法等综合集成方法建立了高速铁路运营安全综合评价体系[11]；胡启洲等人基于价值函数的城市道路交通安全测度模型[12]，对城市道路的安全情况进行评价。在高速铁路及道路评价中，大量学者采用了模糊综合评价法进行分析[13-15]，价值函数的应用较少。由于超级高铁特征评判指标同时包含定性指标与定量指标，结合对各类评价方法的分析，本文将采用价值函数法对超级高铁的特征进行评判，运用熵值法确定评判指标的权重，更加全面、系统地分析与判断数据，解决指标中的不确定问题。并将模糊综合评价法作为对比方法，分析比较两种评价方法的评判过程与结果，判断价值函数法是否适合超级高铁特征评判过程。

2.1 基于TOPSIS价值函数法的超级高铁特征综合评判

TOPSIS价值函数法为一种逼近于理想解的技术，是一种多目标决策方法。该方法的基本思路是定义决策问题的理想解和负理想解，然后在可行方案中找到一个方案，使其距理想解的距离最近，而距负理想解的距离最远[16-19]。TOPSIS价值函数法的评价步骤为：

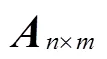
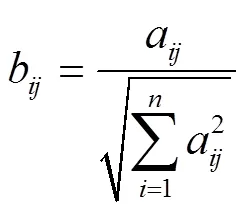
Step3 计算各指标的权重系数。针对超级高铁特征的各个评判指标，笔者运用熵值法计算各指标权重系数，具体步骤如下：

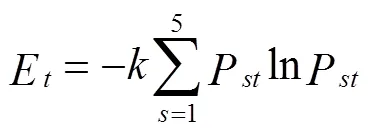
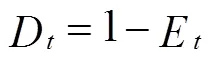
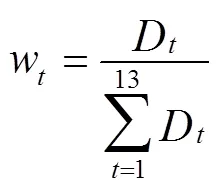
超级高铁特征评判的负理想解为：

2.2 基于模糊综合评价法的超级高铁特征综合评判

模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价[20, 21]。它具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。模糊综合评价法的步骤为：

Step1 根据样本矩阵确定各评价指标的权重系数。基于图1，笔者仍采用熵值法确定13个超级高铁特征评判各指标的权重系数，根据公式（2）~（6）计算得到权重系数。

Step2 确定评价等级。笔者将超级高铁的特征分为五个等级进行评价，即：

=｛优秀，良好，中等，一般，差｝ （13）

对式（13）中的5个等级进行界定，按十分制打分。9分以上为优秀，表明超级高铁的各特征均符合国际标准，为建设者、出行者以及管理者广泛接受；7~9分为良好，表明超级高铁的特征基本符合国际标准，大部分建设者、出行者以及管理者可以接受；5~7分为中等，表明超级高铁的特征有小部分不符合国际标准，一部分出行者不会选择此种交通方式；3~5分为一般，表明超级高铁的特征大部分不符合国际标准，大部分建设者、出行者以及管理者不能接受此种出行方式；低于3分为差，表明超级高铁的特征基本不符合国际标准，不能投入运营。超级高铁特征评判的等级区间如表1所示。

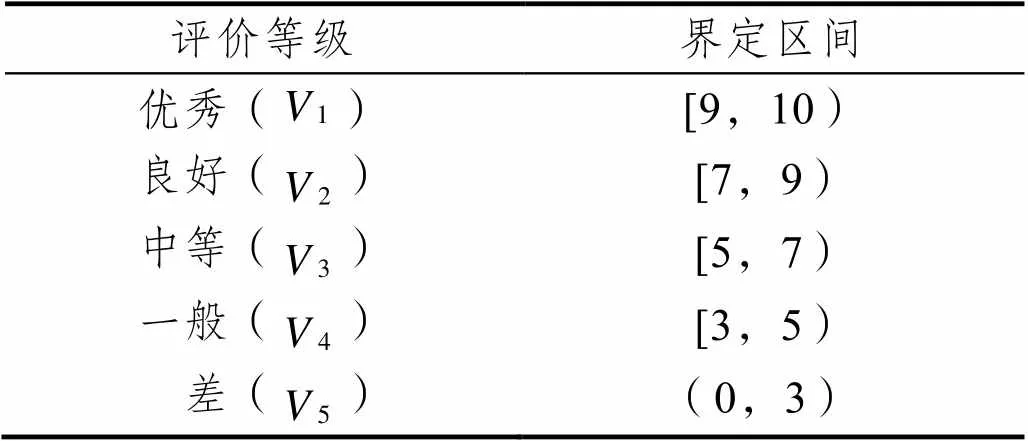
表1 超级高铁特征综合评判等级界定区间

Step4 确定评判等级。对超级高铁特征评判各指标的权重矩阵和单因素模糊评判矩阵进行复合运算，得到超级高铁特征评判模糊综合评判矩结果：

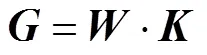
最后按照最大隶属度的原则，确定超级高铁特征评判的最终评判等级。

3 算例分析

根据已建立的超级高铁特征评价指标体系，邀请5位具有专业代表性的专家组成评价小组，并根据现场工作经验对各评价指标进行打分，经过相关分析、汇总计算及处理后，计算相应的指标权重，再分别运用TOPSIS价值函数法和模糊综合评价法进行评价，并将两种不同的评价方法得出的结论进行对比，对本文提出的评价模型进行验证。

3.1 基于TOPSIS价值函数法的超级高铁特征综合评判算例

根据2.1节所述的TOPSIS价值函数法对超级高铁特征评判的步骤，结合相关数据进行算例分析，具体如下：

Step1 获得超级高铁特征评判的初始样本数据。邀请5位具有专业代表性的专家组成评价小组，对超级高铁特征评判13个评判指标进行打分，得到初始样本数据，即：

Step2 建立超级高铁特征评判的决策矩阵。在超级高铁特征评判中，把每个评判指标的平均得分和每个评判级的标准值分别看作TOPSIS价值函数法的决策方案。笔者将超级高铁的特征分为5个等级，每个等级的代表值为：

将5位专家对每项指标的打分求平均数，得到每项评价指标的平均得分，然后与等级的标准值构成决策矩阵，即：

Step3 计算超级高铁特征评判的规范化决策矩阵。根据式（1）得到规范化决策矩阵为：

Step4 计算超级高铁特征评判各指标的权重系数。利用熵值法计算13个评判指标的权重系数，根据式（2）对原始数据矩阵进行标准化，得到标准化数据矩阵。即：

根据式（4）和（5）分别计算超级高铁各评判指标的熵值以及信息熵冗余度。计算结果如表2所示。

表2 超级高铁各评判指标的熵值和信息熵冗余度

根据式（6）确定13个评判指标的权重系数，计算结果如表3所示。

表3 超级高铁各评判指标的权重系数

Step5 构造超级高铁特征评判的规范化加权决策矩阵。根据式（7）得到规范化加权决策矩阵：

超级高铁特征评判的负理想解为：

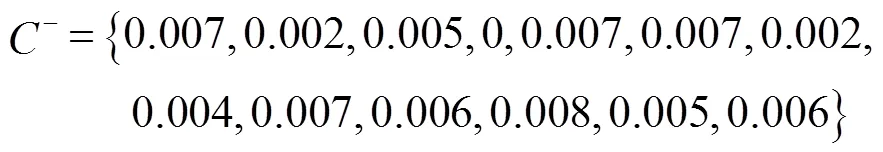
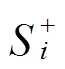
表4 、和计算值

3.2 基于模糊综合评价法的超级高铁特征综合评判算例

根据2.2所述模糊综合评价法对超级高铁特征评判的步骤，结合数据进行算例分析，具体如下：

Step1 根据样本矩阵确定超级高铁特征评判各评价指标的权重系数。根据3.1 Step4可得13个评价指标的权重系数如表3所示。

Step2 确定超级高铁特征评判的等级。将评判等级分为优秀、良好、中等、一般、差五个等级，五个等级的界定区间如表1所示。

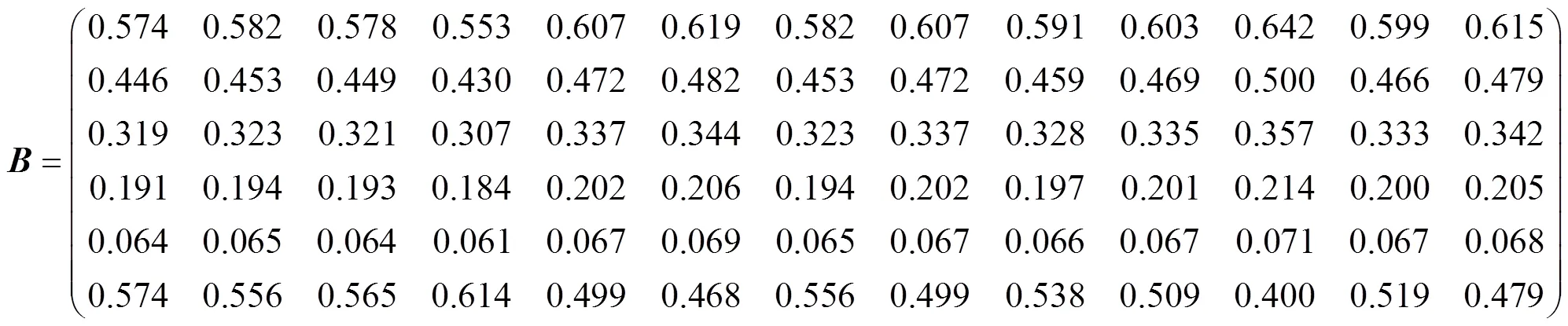
Step3 确定超级高铁特征评判的模糊关系矩阵。根据专家打分情况，得到每个指标的隶属度矩阵，从而得到模糊关系矩阵：

Step4 确定超级高铁特征评判的评判等级。根据式（13）计算评判结果，即：

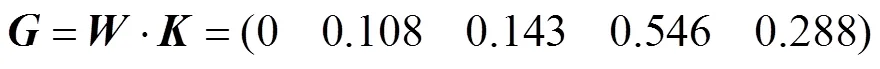
对评判矩阵结果进行分析，按照最大隶属原则，得到超级高铁的评价等级为“良好”。

3.3 两种不同方法对超级高铁特征评判结果的比较

由两种方法对超级高铁特征的评价结果可知，超级高铁的评价等级均为“良好”。但是两种方法在评价过程中有着各自的特点，通过对比分析，得到图2。

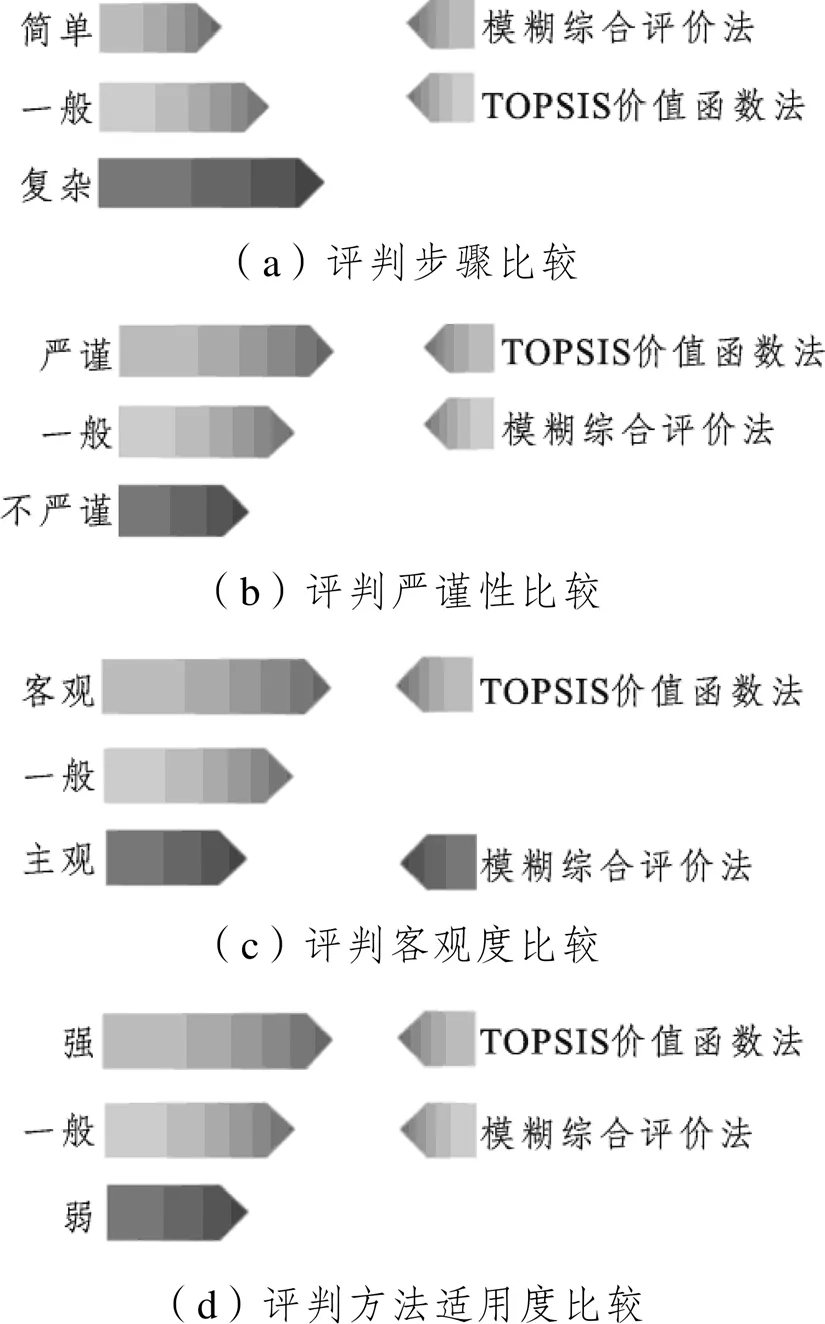
图2 两种评判方法的比较

对比两种评价方法，模糊综合评价法步骤较为简单，评价结果也可以直观体现，但在评价过程中专家的主观因素更多，尤其在超级高铁领域，在没有实际运营的情况下，各位专家对其一些理念与特征的认识没有一个更规范的标准，因此该方法在超级高铁评价领域实用性不高，但此方法可以用在简单且要求不高的评价体系中。相对应的，TOPSIS价值函数评价法过程更加客观与严谨，并且可以将超级高特的特征评判结果与各个等级的标准值进行对比，评价过程更加直观，评价结果也具有客观性与说服力。通过对比分析，TOPSIS价值函数评价法更适用于超级高铁的特征评判体系。

4 结束语

本文将TOPSIS价值函数法和模糊理论综合评价运用于超级高铁的特征评判中，并比较了两种方法对超级高铁的特征评判过程和结果，得出了以下结论：

（1）建立的指标体系符合客观实际，其权重系数利用结构熵权法来确定，更具有客观性与合理性；

（2）分别用两种评价方法对超级高铁的特征问题进行综合评判，得到超级高铁的特征等级均为“良好”；

（3）通过对两种评价方法的比较，得出TOPSIS价值函数法更适合用来对超级高铁的特征进行评判，该评价方法为我国超级高铁未来的安全运营发展提供了参考依据，具有一定的应用意义。

本文的研究也存在一定的不足之处，例如，由于超级高铁还未实际运营，对其特征的评判只能从理论上进行，不能在实际应用中得到验证。在将来的研究中，应该考虑进一步使用仿真软件对超级高铁的特征进行动态的仿真与预测，使研究具有更进一步的实际意义。

[1] 曲鸿. 超级高铁[J]. 城市环境设计, 2019, 118(2): 260-267.

[2] 汤友富. 超级高铁发展趋势及关键问题分析[J]. 铁道建筑技术, 2019, (4): 1-4.

[3] NICK N, SATO Y. Computational fluid dynamics simulation of Hyperloop pod predicting laminar-turbulent transition[J]. Railway Engineering Science, 2020, 28(1): 97-111.

[4] MOSSI M, ROSSEL P. Swissmetro: a revolution in the high-speed passenger transport systems[C]//1st Swiss Transport Research Conference. Ascona: IEEE, 2001: 1-16.

[5] OSTER D, FLA R C. Evacuated tube transportation: U S, 5950543[P]. 1999-09-14.

[6] 沈志云. 关于我国发展真空管道高速交通的思考[J]. 西南交通大学学报, 2005, 40(2): 133-137.

[7] MUSK E. Hyperloop alpha[EB/OL]. 2013[2018-4-13]. http: //www. spacex. com/sites/spacex/files/hyperloop_alpha. pdf.

[8] 张耀平, 于晓东. 真空管道运输安全问题成因分析[J]. 交通运输工程与信息学报, 2006, 4(3): 57-63.

[9] 张耀平. 管道断面尺寸对真空管道交通建设成本与运营成本的影响[J]. 真空, 2012, 49(4): 17-21.

[10] 王迎晗, 陆键, 彭一川. 基于模糊网络分析法(F-ANP)的高速铁路运营安全评价[J]. 中国铁路, 2020(2): 57-65.

[11] 郑丽媛, 高宁波, 胡启洲, 等. 基于集成法的高速铁路运营安全综合评价[J]. 交通信息与安全, 2015, 33(3): 65-70, 86.

[12] 胡启洲, 陆化普. 基于价值函数的城市道路交通安全测度模型[J]. 中国安全科学学报, 2010, 20(6): 45-50.

[13] BAGON A L , TARASYEV A M. Analysis of economic growth models via value function design[J]. Program of the Ural Branch of the Russian Academy of Sciences, 2018, 32(51): 624-629.

[14] BREITEN T, KUNISCH K, PFEIFFER L, et al. Taylor expansions of the value function associated with a bilinear optimal control problem[J]. Annales de l'Institut Henri Poincaré C. 2019, 5(36): 1361-1399.

[15] BABENKO V. Numerical methods for solution of Volterra and Fredholm integral equations for functions with values in L-spaces[J]. Mathematics and Computation, 2016, 291: 354-372.

[16] 梁薇, 王应明. 基于前景理论的不确定TOPSIS多属性决策方法[J]. 计算机系统应用, 2019, 28(3): 36-42.

[17] 武家辉, 王维庆, 王海云, 等. 基于综合权重理论和Fuzzy-TOPSIS综合评价的电网静态电压稳定性分析[J]. 电力系统保护与控制, 2018, 46(23): 77-85.

[18] GHADERI M, RUIZ F, AGELL N, et al. A linear programming approach for learning non-monotonic additive value functions in multiple criteria decision aiding[J]. European Journal of Operational Research, 2017, 3(259): 1073-1084.

[19] LEHRER E, SOLAN E, SOLAN O N, et al. The value functions of Markov decision processes[J]. Operations Research Letters, 2016, 5(44): 587-591.

[20] SOFIA C, MARIA P, WILLIAM S. High speed rail comparative strategic assessments in EU member states[J]. Environmental impact assessment review, 2017, 66 (9): 1-13.

[21] 陈慧阳, 沙明华. 基于模糊综合评价的高速铁路安全运营研究[J]. 西部交通科技, 2017 (12): 77-80.

Comprehensive Evaluation of Hyperloop Characteristics Based on TOPSIS Value Function

GENG Can-xin, SONG Yang, WU Yi-kai

（School of Automation, Nanjing University of Science and Tecnology, Nanjing 210094, China）

In order to observe the grade of the characteristics of Hyperloop more visually, the TOPSIS Value Function method is used to evaluate the characteristics of Hyperloop. Moreover, its evaluation process and results are compared with the Fuzzy Theory. First, from the point of view of “speed, safety, comfort, stability, and economy”, this paper analyzes the factors that affect the characteristics of Hyperloop; in addition, it establishes 13 indexes and the evaluation index system of Hyperloop characteristics. Second, this paper calculates the weight coefficients of 13 indexes by the Entropy Method. Then, combined with the adaptability characteristics of the TOPSIS Value Function and Fuzzy Evaluation Method, the characteristic grade of Hyperloop is evaluated. Finally, the paper compares and analyzes the two evaluation methods to select the method more suitable for the evaluation of Hyperloop. The evaluation result shows that the grade of Hyperloop is “good.” The evaluation steps of the Fuzzy Evaluation Method are relatively simple. However, there are many subjective factors. The evaluation process of the TOPSIS Value Function Method is more intuitive, objective, and rigorous; in addition, the evaluation results are more convincing. This result reflects the superiority of the Hyperloop characteristics. Moreover, it shows that the TOPSIS Value Function Method has high practicability in the comprehensive evaluation of Hyperloop characteristics.

Hyperloop; characteristic evaluation; TOPSIS Value Function; Fuzzy Evaluation Method

1672-4747（2021）02-0101-09

U238

A

10.3969/j.issn.1672-4747.2021.02.012

2020-09-06

中国国家铁路局科研项目（YJ2018-009）；教育部人文社科科学研究项目(18YJAZH028)

耿灿欣（1996—），女，山东潍坊人，硕士研究生，研究方向：交通运输工程、轨道交通规划与管理，E-mail：gengcanxin1216 @163.com

耿灿欣，宋 阳，吴翊恺. 基于TOPSIS价值函数的超级高铁特征综合评判[J]. 交通运输工程与信息学报，2021, 19(2): 101-109.

GENG Can-xin, SONG Yang, WU Yi-kai. Comprehensive Evaluation of Hyperloop Characteristics Based on TOPSIS Value Function [J]. Journal of Transportation Engineering and Information, 2021, 19(2): 101-109.

（责任编辑：李愈）