城市轨道交通-经济复合系统协同发展研究
赏珂祺,帅 斌,黄文成,左博睿
城市轨道交通-经济复合系统协同发展研究
赏珂祺1,3,帅 斌1,2,黄文成1,2,左博睿1,2
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 综合交通运输智能化国家地方联合工程实验室,成都 611756;3. 中国电建集团昆明勘察设计研究院有限公司,昆明 650051)
为探究城市轨道交通与社会经济内在发展联系,构建基于协同学理论的城市轨道交通-经济复合系统协同模型。模型首先基于因子分析筛选复合系统序参量,其次建立改进的差分式协同度模型计算协同度量化指数,最后基于哈肯模型探究演化机制、预测协同发展趋势。以成都市数据为例,应用模型分析2010—2018年复合系统协同演化过程,案例分析表明:复合系统在该阶段内经历两个协同演化周期,于2018年进入更新期(或衰退期)。此外,协同度预测结果显示该复合系统潜在协同水平有降低趋势,应采取措施及时调整。
交通运输经济;协同演化;差分式协同度模型;哈肯模型;城市轨道交通
0 引 言
国务院办公厅于2018年出台《关于进一步加强城市轨道交通建设规划管理的通知》,文件对城市轨道交通发展与经济发展的适应程度提出了更高要求。由此可知,深入探究城市轨道交通与经济的内在发展联系对于推动城市科学发展建设具有重要指导意义。
既有研究将城市轨道交通与经济视为独立系统,通过建立指标体系进而计算耦合度或协同度以判断两者相对发展水平。其中,郭建民[1]集成DEA(Data Envelopment Analysis)模型与主成分分析法构建轨道交通和经济社会发展评价模型以探讨轨道交通建设水平;姬亚鹏[2]通过主成分分析法建立交通与经济评价指标体系以判定两者协同发展程度;王光波[3]集成主成分分析法和耦合协调度模型探究城轨与经济协调作用机理;薛峰[4]基于灰色关联度法构建唐山轨道交通产业与社会经济发展耦合模型以探究其现阶段耦合度类型。
综上可知,现有研究皆是站在静态视角探讨某时刻城市轨道交通与经济发展耦合协调程度,对于两者间的动态协同演进规律鲜有涉及。鉴于此,笔者基于协同学理论,构建城市轨道交通-经济复合系统,以探究时空视角下两者动态协同演化规律,进而明确复合系统所处阶段发展目标及提出管理建议。以成都市为例进行实例探究,以期为城市发展决策提供一定的技术支持。
1 城市轨道交通-经济复合系统协同度计算与预测模型原理
城市轨道交通-经济复合系统(以下称复合系统)由限定区域内的城市轨道交通子系统和经济子系统复合而成。复合系统内部子系统间相互影响、相互渗透,构成了具有特定功能与结构的开放式复杂动态系统,其发展过程具备哈肯自组织系统开放性、非平衡性、非线性和涨落波动性[5]的四个特征,满足系统协同演化条件。
复合系统协同演化指在外部环境的影响以及内部运行机制的调控下,子系统间以及子系统内部各要素相互协调、互相补给、共同发展,使复合系统从无序到有序、从低级到高级[6, 7]的动态发展过程,故协同发展既是系统的发展过程,也是发展目标。以协同度作为判断复合系统协同发展程度的量化指标,在计算协同度之前,需对复合系统的协同发展进行阶段划分。
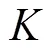

表1 协同度取值区间
计算系统协同度首先需确定子系统序参量。序参量[6]为确定系统的宏观行为并表征系统有序化程度的参数变量,演化方向决定系统发展方向,对合理促进城市轨道交通与经济的协同管理尤为重要。以宏观代表性、系统性、可量化为原则,从规模结构性、效益性两方面出发,参考既有文献[1-6, 11],基于德尔菲法讨论得出潜在代表子系统发展现状指标作为候选序参量,具体如表2所示。其后将基于目标系统指标实际数据采用因子分析法等方法确定实际序参量。

表2 子系统序参量备选指标
明确系统序参量进而构建协同度模型以计算复合系统协同度,最后基于哈肯模型[13, 14]预测复合系统未来协同发展趋势。基于系统序参量的作用原理,哈肯提出绝热消去法,用数学方法处理系统参量以构建演化方程,判断各项参数是否满足绝热近似假设并求解势函数,进而推算系统的序参量方程和演化方程组,以此探析复合系统的自组织协同演化过程。
2 模型应用流程
2.1 序参量贡献度计算
由于序参量各项指标的数量级、单位不统一,需对指标进行标准化处理。正功效型和负功效型指标具有不同内涵,在进行归一化处理时需区别计算。其中正功效序参量贡献度如式(1),负功效型序参量贡献度见式(2):


2.2 子系统有序度计算

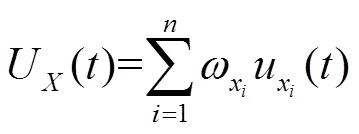
2.3 差分式协同度测算


其中,

2.4 协同度预测
基于哈肯模型,确定复合系统运动方程并拟合预测未来系统演化方向。
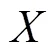
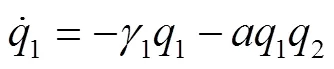
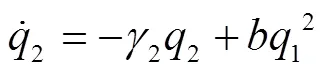
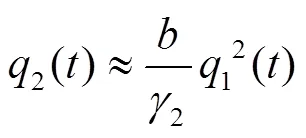
结合公式(7)~(8),对其进行离散化处理得到公式(10)~(11):


以子系统有序度作为子系统状态参量,当城轨子系统为复合系统序参量,演化方程如下式所示:

当经济子系统为复合系统序参量,演化方程如下式所示:

基于有序度及演化方程可有效把握系统阶段演化规律进而合理预测复合系统未来发展趋势。
3 实 例
以成都市2010年至2018年指标数据为样本,基于因子分析法从表2指标中筛选得到子系统序参量如表3与图1所示。

图1 子系统序参量


表3 子系统序参量

计算子系统有序度及复合系统协同度,结果如表4所示(2019—2022年为预测结果)。

表4 复合系统协同发展指数计算
基于计算结果分析可知:
(1)近年成都市城轨子系统与经济子系统有序度整体均呈上升趋势,而复合系统协同度于2010—2012年经历快速的完整协同演化周期后于2013年进入新一轮的演化周期。
(2)2010至2018年成都地铁网络尚未完善,发展滞后于城市经济,城轨子系统有序度始终低于经济子系统。因此,2012年协同度升至0.9并未达到真正意义的协同。
结合差分变化率分析复合系统实际协同发展过程,在成都市轨道交通“十二五”规划等政策以及经济系统的正向推动下,2010年城市轨道交通起步阶段发展迅速,多项指标从无到有,涨势迅猛。以客流量为典型,2011年地铁总客流较2010年增长356.7%(见表1)。导致两年内城轨子系统差分变化率分别高达10.5和5.28;同期,成都“十二五建设”及轨道交通推动市内经济发展成效初显,经济子系统2012年差分变化率由0.1增长至0.8。两子系统差分变化率的同向增加最终导致复合系统协同演化进程加速,2012年复合系统协同度直达更新期,并正向演化于2013年开始新一轮演化周期。

图2 复合系统协同发展指数计算与预测
分析图2可知:
(1)城轨-经济复合系统具有明显的非线性特征并产生了复杂的正负反馈效应以构成相对有序的时空结构。2012年城轨子系统在经济子系统的正反馈推动作用下迅速发展,差分变化率与经济子系统差值超过一定程度以致系统潜在偏向发展而结构失衡,协同效应降低。此时负反馈机制削弱系统内外部变化对系统的影响以使系统恢复稳态,最终在非线性机制的相互作用下,两子系统的差分变化率逐渐接近,协同效应增大,协同度再次升高。
(2)“通过涨落达到有序”是自组织理论的基本原理之一。成都地铁开通初期,短时期内复合系统开始初始演化,城轨子系统的建立引起复合系统发生“巨涨落”现象,打破系统原有状态,促使系统开始新的周期演化进程。期间两子系统积极寻求契合的协同发展模式,持续培育新增长点,以此不断循环,在不平衡中寻找新的稳态。
(3)基于哈肯模型预测未来协同发展水平结果显示,2021年复合系统再次进入协同演化更新期。2019—2022年成都市城市轨道交通子系统有序度始终呈递增趋势,而经济子系统2010年至2020年呈上升趋势,2020年后有序度呈下降趋势;复合系统协同发展在衰退期(或更新期)中逐步接近发展阈值,发展速度减缓向0趋近,系统进入演化阶段末端并面临潜在负向演化趋势。
在此阶段,成都城市规划管理者需采取对应措施积极引导复合系统协同发展:
① 为避免经济子系统有序度下降、两子系统差分变化率差值增大而导致复合系统协同发展负向演化,应推进经济系统全面创新,坚持深化改革,扩大开放,积极寻求城市经济新增长途径以推动经济子系统持续发展。
② 2021年后,城市轨道交通子系统有序度持续稳步上升并超越经济子系统有序度,表明此期间成都复合系统协同发展趋势为城轨发展逐渐超前于经济发展。此时应适当调整城轨建设发展速度,合理把握其建设规模和节奏,坚持“量力而行,有序推进”、“因地制宜、经济适用”等原则,控制部分轨道交通产业的过度超前发展,提高城市轨道交通发展质量,确保与城市经济发展水平相协调。
4 结 论
(1)基于协同学理论研究城市轨道交通-经济复合系统的协同发展过程,构建差分式协同度模型计算复合系统协同度,运用哈肯模型探究协同演化机制,预测复合系统未来发展趋势,以把握复合系统演化规律,为城市轨道交通与经济协调可持续发展提供决策参考。
(2)计算分析成都市2010年至2018年“城市轨道交通-经济”复合系统协同度,并合理预测其发展趋势,结果表明复合系统在研究时段共经历两次演化周期,目前已进入协同发展更新期(或衰退期),与实际情况贴合。
[1] 郭建民, 韩林飞, 马莉莉. DEA视角下基于主成分分析的城市轨道交通建设水平研究[J]. 北京交通大学学报, 2015, 39 (1): 90-94.
[2] 姬亚鹏. 一体化背景下京津冀交通与经济协调发展评价研究[D]. 北京: 北京交通大学, 2016.
[3] 王光波. 城市轨道交通与社会经济发展耦合协调度分析[D]. 重庆: 重庆大学, 2018.
[4] 薛锋, 邹彪, 戴文涛. 唐山市轨道交通产业与区域发展的关联分析[J]. 综合运输, 2018, 40 (5): 107-110.
[5] 冷碧滨, 吉雪强, 胡俏, 等. 系统自组织演化流率基本人树模型的构建和应用——基于规模养殖生态能源系统的反馈仿真[J]. 系统工程理论与实践, 2019, 39 (10): 2689-2701.
[6] 哈肯 H. 协同学引论[M]. 徐锡申等译. 北京: 原子能出版社, 1984.
[7] HERMANN H. Synergetics: an introduction: non equilibrium phase transitions and self-organization in physics, chemistry, and biology[J]. Physics Bulletin, 1978, 29(4): 181.
[8] 曹炳汝, 樊鑫. 港口物流与腹地经济协同发展研究——以太仓港为例[J]. 地理与地理信息科学, 2019, 35 (5): 126-132.
[9] 汪良兵, 洪进, 赵定涛, 等. 中国高技术产业创新系统协同度[J]. 系统工程, 2014, 32 (3): 1-7.
[10] 张庆普, 胡运权. 城市生态经济系统复合Logistic发展机制的探讨[J]. 哈尔滨工业大学学报, 1995 (2): 131-135.
[11] 范英飞, 章国鹏, 徐梦清, 等. 成渝城市群经济与交通运输通道协同演化表征方法[J]. 交通运输系统工程与信息, 2018, 18 (3): 234-241.
[12] 龙江, 徐爱农, 曹钟勇. 城市轨道交通发展的阶段性研究[J]. 铁道学报, 1998 (4): 127-131.
[13] YANG C, LAN S L, WANG L H. Research on coordinated development between metropolitan economy and logistics using big data and Haken model[J]. International Journal of Production Research, 2019, 57 (4): 1-14.
[14] H. 哈肯. 高等协同学[M]. 郭治安译. 北京: 科学出版社, 1989.
[15] 武玉英, 魏国丹, 何喜军. 基于耦合系数模型的高技术制造业与要素协同度测度及实证[J]. 系统工程, 2017, 35 (7): 93-100.
[16] 余佳每,王沁,苏佳琳. 基于熵权效率的交通运输与经济发展的协调性分析[J]. 交通运输工程与信息学报, 2020, 18(2):177-184.
Research on the Collaborative Development of a Composite System for an Urban Rail Transit - economy
SHANG Ke-qi1, 3, SHUAI Bin1, 2, HUANG Wen-cheng1, 2, ZUO Bo-rui1, 2
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National United Engineering Laboratory of Intergrated and Intelligent Transportation, Chengdu 611756, China; 3. Power China Kunming Engineering Corporation Limited, Kunming 650051, China)
In order to explore the synergy between urban rail transit and economic development, a composite system for an urban rail transit economy was constructed based on synergy theory. First, the order parameters of the system were screened based on a factor analysis. Second, an improved difference fraction synergetic model was established to calculate the synergetic degree of the composite system. Finally, based on the Haken model, the co-evolution curve of the urban rail transit economy composite system was fitted to predict future development trends. Taking Chengdu as an example, the case analysis showed that the composite system experienced two coevolution cycles and entered a period of decline (self-renewal period) in 2018.In addition, the synergetic prediction results show that the potential synergetic level of the composite system will decrease in the future and should be adjusted in time.
transportation economy; co-evolution; differential synergy model; hawking model; urban mass transit time
1672-4747(2021)02-0084-07
F511.3
A
10.3969/j.issn.1672-4747.2021.02.009
2020-08-11
国家自然科学基金项目(71173177);国家铁路局科技计划项目(KF2013-020,KF2014-041);四川省科技厅软科学项目(20RKX0728);西南交通大学研究生创新实验实践项目(YC201507103);西南交通大学研究生学术培养提升计划(跨学科创新培育)专题(2018KXK04)
赏珂祺(1996—),女,汉族,云南陆良人,硕士研究生,研究方向为交通运输经济,E-mail:1016125137@qq.com
帅斌(1966—),男,汉族,四川乐山人,博士,教授,研究方向为交通运输经济、危险品运输路网建模与规划、危险品运输系统评价等,E-mail:bsh67@126.com
赏珂祺,帅斌,黄文成,等. 城市轨道交通-经济复合系统协同发展研究[J]. 交通运输工程与信息学报,2021, 19(2): 84-90.
SHANG Ke-qi, SHUAI Bin, HUANG Wen-cheng, et al. Research on the Collaborative Development of a Composite System for an Urban Rail Transit - economy[J]. Journal of Transportation Engineering and Information, 2021, 19(2): 84-90.
(责任编辑:刘娉婷)

