Distributed solving Sylvester equations with fractional order dynamics

Songsong Cheng · Shu Liang 2 · Yuan Fan

Abstract This paper addresses distributed computation Sylvester equations of the form AX+XB=C with fractional order dynamics. By partitioning parameter matrices A, B and C, we transfer the problem of distributed solving Sylvester equations as two distributed optimization models and design two fractional order continuous-time algorithms, which have more design freedom and have potential to obtain better convergence performance than that of the existing f irst order algorithms. Then,rewriting distributed algorithms as corresponding frequency distributed models, we design Lyapunov functions and prove that the proposed algorithms asymptotically converge to an exact or least squares solution. Finally, we validate the eff ectiveness of the proposed algorithms by providing a numerical example

Keywords Fractional order calculus · Distributed optimization · Sylvester equation · Frequency distributed model ·Convergence

1 Introduction

Linear matrix equations computation is an important and attractive problem in many f ields, such as image processing,control theory, and machine learning [ 1- 3]. Sylvester equations, as a special class of linear matrix equations, received many research attention [ 4- 6]. Many methods were designed to obtain exact or least squares solutions of Sylvester equations in centralized schemes [ 6- 8].

However, in some big data or complex systems circumstances, the dimension of Sylvester equations is very large.Conventional centralized algorithms are diffi cult to solve high-dimensional Sylvester equations. Thanks to the favourable abilities of computation and communication, distributed computation schemes attracted many research attention[ 9- 11]. Deng et al. [ 12] proposed a distributed algorithm to obtain an exact solution of Sylvester equations. Considering that Stein equations in the form ofX+AXB=Chas no solution, Chen et al. [ 13] developed a distributed algorithm to achieve a least squares solution for a special case thatA,BandChave standard Row-Column-Column structure. For linear matrix equationsAXB=C, Zeng et al. [ 14] considered eight standard structures ofA,BandCand developed four distributed algorithms to attain a least squares solution.

Fractional order theory was developed 300 years ago and attracted many scholars’ attention in systems theory [ 15- 17],signal processing [ 18- 20] because of the advantages on system modelling and more design freedom. As far as we know,almost all of the centralized and distributed computations of Sylvester equations are designed based on the integer order iteration law. The objective of this paper is to design distributed algorithms with fractional order dynamics to solve Sylvester equations. Because of more design freedom of the fractional order calculus, we try to obtain that the fractional order algorithm can achieve better convergence performance than that of the integer order counterpart. The main contributions of this paper are listed as follows.

1. A universal distributed optimization model is introduced to handle any type of standard partitioning of matricesA,BandC.

2. In comparison with [ 12- 14], we design two distributed algorithms with fractional order dynamics and prove that the proposed algorithms converge to an exact or least squares solution.

The rest of this paper is organized as follows. Section 2 presents some preliminaries in matrices, fractional order calculus, graph theory, and formulate the problem of distributed solving Sylvester equations, while Sect. 3 models the problem of solving Sylvester equations as two distributed optimization problems, designs two algorithms with fractional order dynamics and shows that proposed algorithms asymptotically converge to an exact or least squares solution. Section 4 provides a numerical example to illustrate the eff ectiveness of the proposed algorithm and Sect. 5 concludes this paper.

2 Preliminaries and problem formulations

2.1 Notations

2.2 Fractional order calculus

Def inition 1 (See[ 21]) For a given functionf(x), theαth order Caputo derivative is

2.3 Graph theory

Assumption 1 The undirected graph G is connected.

2.4 Problem formulation

Consider a problem of solving the following Sylvester equation:

whereA∈ℝm×m,B∈ℝr×r, andC∈ℝm×rare given matrices, andX∈ℝm×ris the solution to be achieved.

In the scheme of distributedly solving ( 3) with the aid of multi-agent systems, theith agent only holds theith subblocks parameter matricesA,B, andC, and exchanges information with their neighbors. For instance, matricesA,B, andCare partitioned as the Row-Column-Column structure,namely,

Remark1 The Row-Column-Column partition in ( 4) is presented as an example to decouple coeffi cient matricesA,B, andC. Actually, with the aid of augmented technique, the decoupling in ( 8) can handle any partition ofA,B, andC.

3 Main results

In this section, we design two algorithms to obtain an exact solution and a least-squares one, respectively. Firstly, we design an algorithm to obtain the exact solution.

3.1 Obtaining an exact solution

According to ( 8), we model the following optimization problem.

It can be verif ied that the problems ( 3) and ( 9) are equivalent. Based on ( 9), we construct an augmented Lagrangian function as

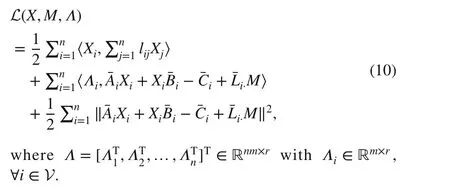
According to ( 10), we design the following fractional order continuous-time optimization algorithm from primaldual viewpoint, i.e., gradient descend for primal variablesXandMand gradient ascent for the dual variableΛ, and both primal and duel variables governed by the fractional order update law.

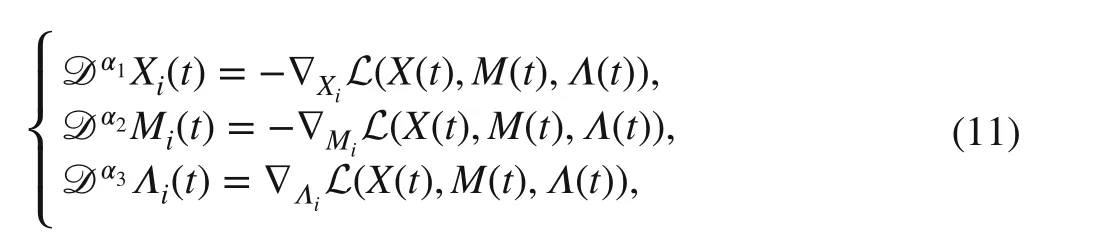
where 0＜α1,α2＜2 , 0＜α3＜1 , ∇XiL(·,·,·) , ∇MiL(·,·,·) ,and ∇ΛiL(·,·,·) are gradients of L on variablesXi(t) ,Mi(t) ,andΛi(t) , respectively. Based on ( 10), the detailed dynamics ofXi(t) ,Mi(t) , andΛi(t) are expressed in Algorithm 1.

?

Remark2 In Algorithm 1, we design a distributed algorithm to solve Sylvester equations with fractional order iteration dynamics. Compared with conventional integer order scheme, the proposed algorithm has more design freedom and has potential to obtain better convergence performance than that of the conventional first order counterpart.

For Algorithm 1, we provide the following convergence results.

Theorem 1Under Assumption1,letXi(t) ,Mi(t) ,andΛi(t)be generated by Algorithm1.If0＜α1,α2,α3＜1 ,thenXi(t)asymptotically converges to exact solutions of Sylvester equations.

ProofBy introducing Kronecker product, we rewrite the dynamic ofXi(t) in Algorithm 1 in the following column form

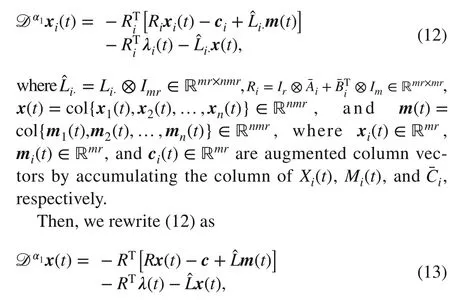
According to the Lasalle invariance principle, this completes the proof.

◻

Next, we show a convergence result of Algorithm 1 by extendingα1andα2from interval (0, 1) to interval (1, 2).

Theorem 2Under Assumption1,letXi(t) ,Mi(t) ,and Λi(t)be generated by Algorithm1.If1＜α1=α2＜2 andα1+α3=2 ,thenXi(t)asymptotically converges to an exact solution of Sylvester equations.

ProofSimilar to the proof of Theorem 1 and note thatα1=1+1andα2=1+2, we rewrite the dynamics of Algorithm 1 as follows:

Apparently,α1=1+1andα1+α3=2 implies1+α3=1 .As a result,

Based on Lemma 1, we have the following frequency distributed model of ( 20):

Based on ( 22), we design the following Lyapunov function

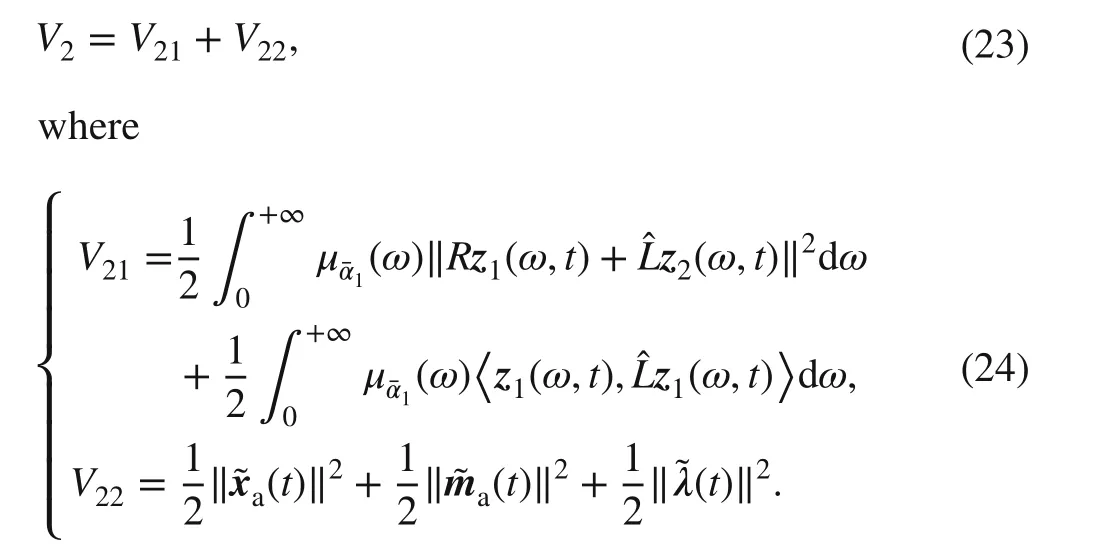
Note that

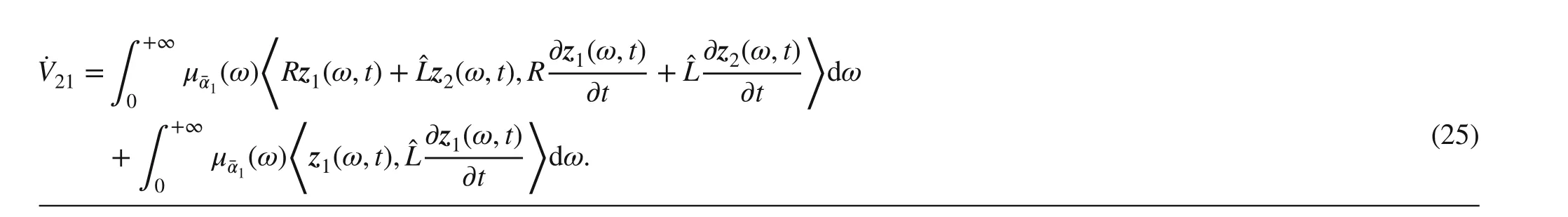
Substituting ( 22) into ( 25),

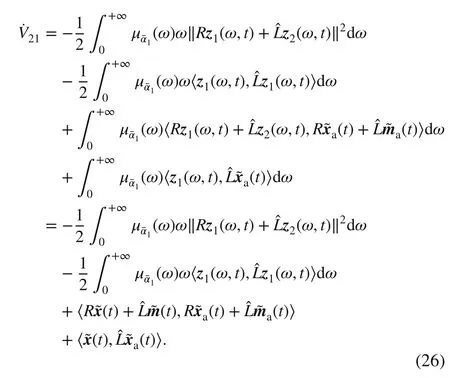
Similarly,

Combining ( 28) with ( 27) yields

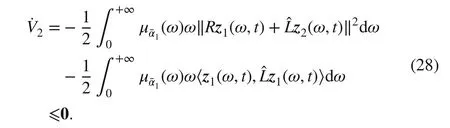
According to the Lasalle invariance principle, this completes the proof.

◻

Remark3 In [ 12], the authors utilized derivative feedback in their algorithm and then obtained the convergence result.In this paper, we design Algorithm 1 based on augmented Lagrangian function and does not need derivative feedback.

3.2 Obtaining the least squares solution

Based on ( 9), Algorithm 1 can achieve exact solutions of ( 3). However, Algorithm 1 cannot handle the circumstance that ( 3) has no exact solution. Then, we design a novel optimization model to achieve least squares solution next.

According to ( 8), we develop the following distributed optimization problem

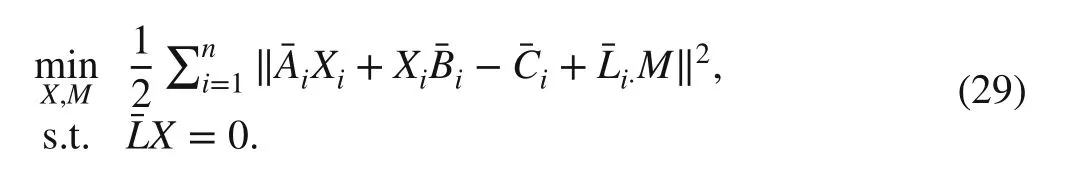
It can be verif ied that the problems ( 3) and ( 29) are equivalent in the sense of least square. Based on ( 29), we construct an augmented Lagrangian function as

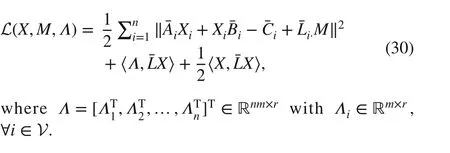
According to ( 30), we design the following fractional order continuous-time optimization algorithm from primal-dual viewpoint, i.e., gradient descend for primal variablesXandMand gradient ascent for the dual variableΛ, and both primal and duel variables governed by the fractional order update law.

images/BZ_99_418_2697_455_2731.pngimages/BZ_99_660_2697_697_2731.pngimages/BZ_99_892_2697_929_2731.pngimages/BZ_99_505_2822_551_2857.pngimages/BZ_99_705_2822_748_2857.pngimages/BZ_99_1043_2822_1086_2857.pngimages/BZ_99_1626_2822_1669_2857.pngimages/BZ_99_510_2877_555_2911.pngimages/BZ_99_763_2877_807_2911.pngimages/BZ_99_1388_2877_1432_2911.png

ProofBy introducing Kronecker product, we rewrite the dynamic ofXi(t) in Algorithm 2 in the following column form:

Considering the equilibrium of ( 33)

According to the Lasalle invariance principle, this completes the proof.

◻

Next, we show a result by extendingα1andα2from interval (0, 1) to interval (1, 2).

Theorem 4Under Assumption1,letXi(t) ,Mi(t) ,and Λi(t)be generated by Algorithm2.If1＜α1=α2＜2 andα1+α3=2 ,thenXi(t)asymptotically converges to the least squares solution of Sylvester equations.

ProofSimilar to the proof of Theorem 1 and note thatα1=1+1andα2=1+2, we rewrite the dynamics of Algorithm 2 as follows:

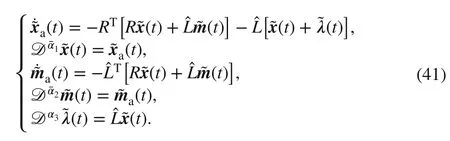
Sinceα1=1+1andα1+α3=2 implies1+α3=1 . As a result,

According to Lemma 1, we have the following frequency distributed model of ( 41)

Substituting ( 43) into ( 46),

Similarly,

Combining ( 49) with ( 48),

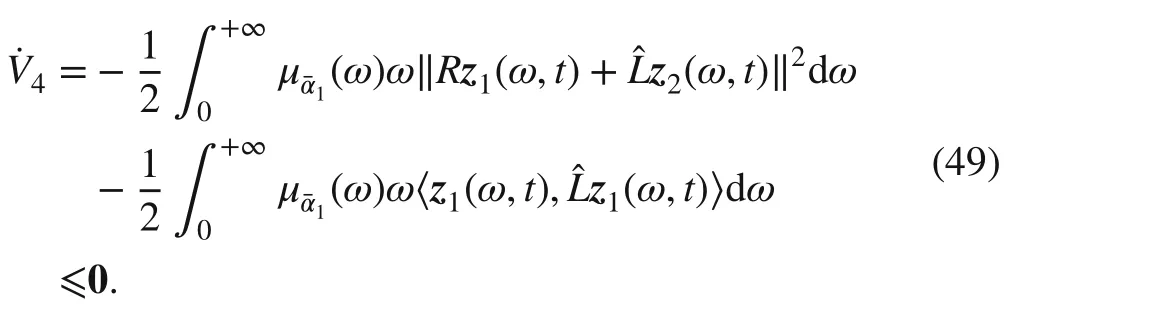
Following from the Lasalle invariance principle, this completes the proof.

◻

Remark4 For distributed solving Sylvester equation ( 3), we decoupled it as ( 8). Then, one utilized consensus constrain as an objective function and the Sylvester equation as an equation constrain in [ 12] and Sect. 3.1 of this paper. However,the corresponding optimization problem ( 9) is only eff ective for exact solutions. Moreover, we developed a novel distributed optimization model ( 29), which is eff ective for least squares solutions.Remark5 Both in Algorithms 1 and 2, the dynamics can be viewed as a class of stable linear time-invariant fractional order systems. Consider a stable linear time-invariant fractional order system Dαx(t)=Ax(t) , which has a fast response but chattering trajectory ifα∈(1,2) , while it has a slow response but smooth trajectory ifα∈(0,1) .In comparison with [ 12- 14], the proposed algorithms with fractional order dynamics have more design freedom. Therefore, we can f ind a proper update order to adjust the tradeoff between the response rate and the smooth trajectory to obtain better convergence performance than that of the f irst order algorithms.

Fig. 1 The trajectories of estimation of X11

Fig. 2 The trajectories of estimation of X21

Fig. 3 The trajectories of exact solution error ‖AX+XB-C‖

4 Numerical example

In this section, we provide an example to validate the eff ectiveness of the proposed algorithm with the following three cases

1. Fractional order dynamics withα1=α2=α3=0.95;

2. integer order dynamics withα1=α2=α3=1.00; and

3. fractional order dynamics withα1=α2=1.05,α3=0.95,

where the fractional order operators of this example are implemented via a piecewise numerical approximation algorithm in the frequency domain [ 23].

Consider a Sylvester equation with the Row-Column-Column structure, whose parameter matrices are randomly chosen as

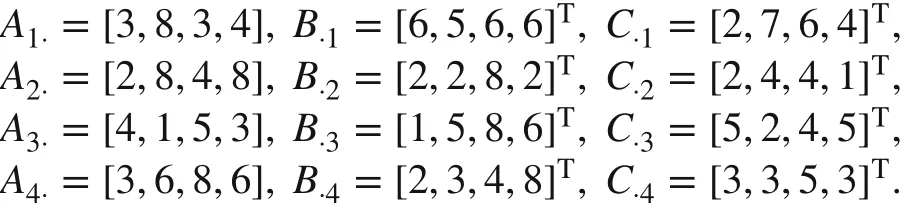
It is not hard to verify that the corresponding solution is

We solve the Sylvester equation with the aid of a multi-agent system, where four agents are connected by an undirected circular graph and theith agent has access to sub-blocksAi·,B·i, andC·i.

We present the trajectories of elementsX11(t) ,X21(t)and exact solution error ‖AXi(t)+Xi(t)B-C‖ in Figs. 1,2 and 3, where “A-i” denotes the corresponding curve of agenti. The simulation results illuminate that the proposed algorithm with fractional order between 0 and 2 asymptotically achieves the solution of the Sylvester equation.Moreover, with more design freedom of fractional order,we obtain better convergence performance than that of the f irst order counterpart.

5 Conclusions

In this paper, we have constructed two distributed optimization models to achieve the exact or least squares solutions of Sylvester equations. We have proposed two distributed algorithm with fractional order dynamics from the primal-dual viewpoint. By transferring the proposed algorithms into corresponding frequency distributed models, we designed Lyapunov functions and then proved the asymptotic convergence of proposed algorithms.

AcknowledgementsThis work was supported in part by the National Natural Science Foundation of China (Nos. 61903027, 61973002), and in part by the National Postdoctoral Program for Innovative Talents(BX20180346), and in part by the General Financial Grant from the China Postdoctoral Science Foundation (2019M660834), and in part by the Anhui Provincial Natural Science Foundation (No. 2008085J32).