外延石墨烯纳米带中纯自旋流的实现

陈 兴

（合肥工业大学 电子科学与应用物理学院，安徽 合肥 230601）

0 引 言

摩尔定律指出，集成电路上可以容纳的晶体管数目大约每18个月翻一倍，即处理器的性能每隔两年便会翻一倍，随着晶体管集成度的增加，器件的热问题对其性能的影响越来越大。为了解决这个问题，电子的另一自由度自旋开始受到人们的关注，并诞生了一门交叉学科，即热自旋电子学。在热自旋电子学中，纯自旋流器件（即器件中两种自旋电子沿相反方向流动，并且大小相等，导致器件中的净电荷流为0）具有许多优良的性能，如更快的速度、更低的功耗以及更高的集成度，被认为是解决集成电路热问题的突破口。

石墨烯具有优异的电学性能和磁学性能，由标准的正六边形蜂窝结构重复单元构成。正因为这样的正六边形结构，所以裁剪的时候会由于方向不同导致其边缘结构不同。其中锯齿型石墨烯纳米带（Zigzag Graphene Nanoribbons，ZGNRs）具有边缘局域态和边缘磁性，被认为是构建自旋电子器件的理想材料之一。现有研究表明，可以通过诸多手段对ZGNRs进行调控实现纯自旋流，如对ZGNRs器件电子磁化方向进行调控来实现纯自旋流[1]。此外，在ZGNRs的中心引入不同大小反量子点也可以实现纯自旋流[2]。本文对锯齿型石墨烯纳米带进行外延使之双边具有等腰三角形外延结构，研究不同长度腰长对纳米带电子输运和热电输运的影响。计算结果表明，在具有该结构的锯齿型石墨烯纳米带中可以实现纯自旋流。

1 计算模型和方法

本文以宽度为六条链的锯齿型石墨烯纳米带单胞为基础，复制展开，形成六条链宽的无限长双端器件模型，该模型包括左电极（Left lead），中心散射区（Center scattering region）以及右电极（Right lead）3个部分，结构如图1（a）所示。以铁磁态的器件为研究对象，研究了在中心区的两个边缘外延出类等腰三角形结构对器件热输运性质的影响，将外延等腰三角形的腰长为一个碳二聚体的模型记为W1模型，如图1（b）所示。当外延等腰三角形的腰长增加到两个碳二聚体时，记为W2模型，如图1（c）所示。W3模型为外延腰长为3个碳二聚体的等腰三角形，如图1（d）所示。左电极为高温区，右电极为低温区，左右电极的温差为ΔT。由于外延部分和石墨烯纳米带的边缘碳原子只和相邻的两个碳原子成键，所以为了让模型更加稳定，使用氢原子来饱和外延部分和纳米带边缘的碳原子[3]。

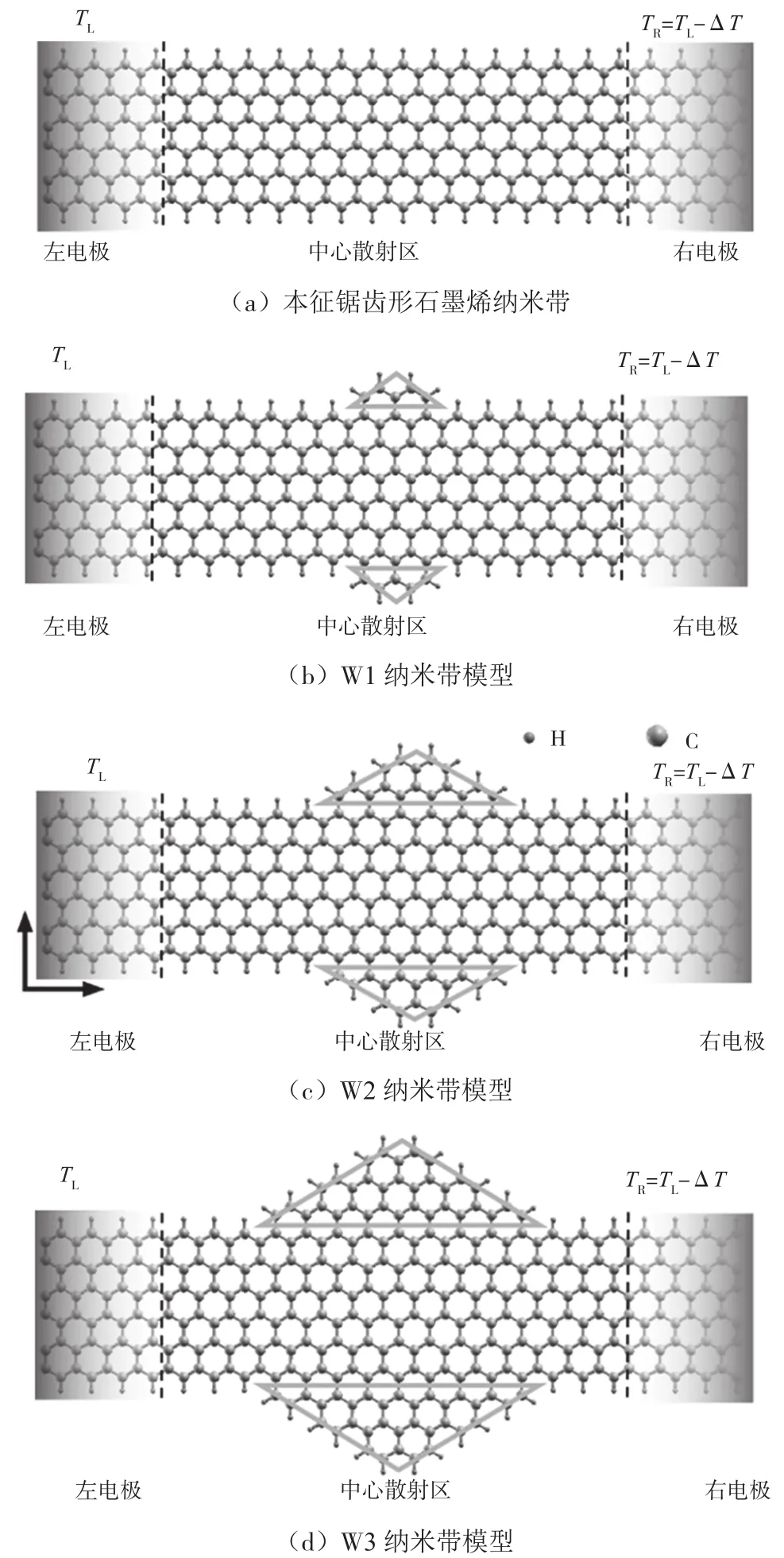
图1 器件模型

本文使用siesta程序进行结构弛豫，力收敛到0.05 eV/A，并且结合非平衡格林函数（Non-equilibrium Green’s Function，NEGF），采用Nanodcal软件包来进行量子输运计算[4,5]。自旋相关透射谱的计算公式为：

式中，Gr（Ga）是散射区的延迟（超前）格林函数；ΓL（ΓR）是描述左（右）电极与中心区耦合的线宽函数。自旋相关电流的计算公式为：

式中，e是电子电荷；h是普朗克常量；fL(E,T)（fR(E,T)）是左（右）电极的费米狄拉克分布[6,7]。在线性响应区，自旋相关电导G↑(↓)和塞贝克系数S↑(↓)的计算公式为：

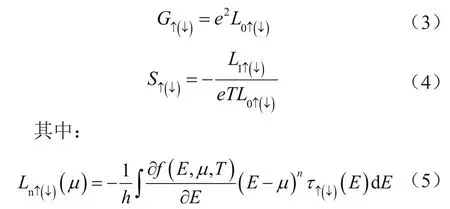
在低温区，不同自旋电子的塞贝克系数可以近似为：

式中，EF是费米能级；kB是玻尔兹曼常数。可以看出，塞贝克系数S↑(↓)与透射系数τ↑(↓)成反比，与透射谱的斜率成正比[8]。因此，需要调控器件透射系数和透射谱的斜率来改善器件的塞贝克系数。

2 研究结果与讨论

2.1 输运性质

为了研究双边外延等腰三角形的腰长对ZGNR输运性质的影响，分别计算了本征、W1（腰长为1个碳二聚体）、W2（腰长为两个碳二聚体）以及W3（腰长为3个碳二聚体）双端器件模型的透射谱，分别如图2（a）、图2（b）、图2（c）以及图2（d）所示。

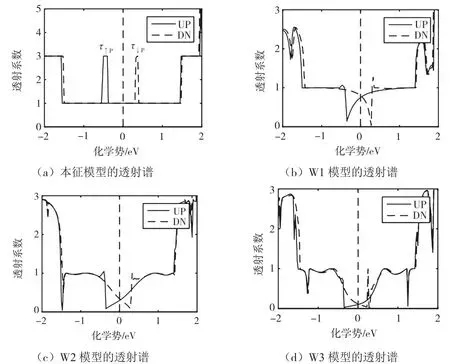
图2 透射谱

与本征体系（图2（a））相比，器件的透射谱发生了显著的变化。本征6-ZGNR的自旋向上电子透射系数τ↑和自旋向下电子透射系数τ↓分别在（-0.52，-0.4）eV和（0.32，0.37）eV区间内为3，将这两个峰值记为τ↑P和τ↓P，这两个峰值是因为不同自旋的电子分别在对应能量范围内存在两个边缘态通道和一个体态通道。τ↑和τ↓在（-0.30，0.30）eV区间内均为 1。而在W1模型中，双边外延等腰三角形同时破坏了ZGNR两个边缘结构的完整性，抑制了电子在纳米带两个边缘的渡越能力，透射谱在费米能级附近形成“X”形交叉，τ↑P和τ↓P均由3降低到1.29以下，在（-0.38，1.45）eV和（-1.50，0.30）eV区间内的τ↑和τ↓也由1降低到1以下。并且τ↑和τ↓分别在能量点约-0.35 eV和0.28 eV处降至约0.15和0.02，形成了两个透射谷，这是费米能级处的“X”形透射谱形成的关键，因此τ↑在（-0.35，1.08）eV区间内随着能量的增加而增加，τ↓在（-0.80，0.28）eV区间内随着能量的增加而减少。然而，在施加温度梯度后，发现器件的自旋塞贝克系数都很小，几乎为0（如图3（a））。将外延等腰三角形的腰上增加到两个碳二聚体（W2模型）进一步降低了电子的渡越能力，τ↑和τ↓在（-0.35，1.08）eV和（-0.80，0.28）eV区间内与W1模型相比有了明显降低但变化规律与W1类似，且费米能级附近的“X”形交叉更加明显。因此，虽然器件的透射能力降低了，自旋塞贝克系数却随着透射谱曲线斜率的增大而增大（如图3（b））。在W3模型中，τ↑P和τ↓P均降低到 1 以下，τ↑和τ↓在（-0.35，1.08）eV和（-0.80，0.28）eV区间内再次降低，并且透射谱曲线变得更加平缓，但“X”形交叉依然存在，而且器件的自旋塞贝克系数进一步增大[8]。3种模型在不同温度下的自旋塞贝克系数如图3所示。

图3 3种模型在不同温度下的自旋塞贝克系数

2.2 热电性质

接下来分别计算了不同器件的两种自旋电子在费米能级附近的塞贝克系数，从左到右依次是W1、W2和W3器件模型的计算结果。如图3所示，其中纵坐标为不同自旋电子的自旋塞贝克系数S↑(↓)，横坐标是器件的化学势，还考虑了温度对器件自旋塞贝克系数的影响，其中图3（a）、图3（b）以及图3（c）为温度T=100 K下的计算结果，图3（d）、图3（e）以及图3（f）为T=200 K的结果。从计算结果可以看出，自旋塞贝克系数的符号与对应自旋电子的透射曲线斜率相同（如图2（b）、图2（c）、图2（d））。由于费米能级附近的透射谱呈现“X”形交叉，所以费米能级附近的不同自旋电子的自旋塞贝克系数相反（如图3（a）），表示不同自旋电子在热温度梯度ΔT的驱动下向相反的方向流动，说明该结构可以用于获得纯自旋流。更重要的是，外延等腰三角形的腰长会影响自旋塞贝克系数S↑(↓)的大小，在W1体系中，器件的自旋塞贝克系数几乎为0，当外延等腰三角形的腰长由1个碳二聚体增加到2、3个碳二聚体，τ↑(↓)的减小和k↑(↓)的增大导致器件的S↑(↓)增大（如图3（b）、图3（c））。另一方面，对于同一器件模型，温度T的升高也会导致器件的自旋塞贝克系数S↑(↓)增大（如图3（d）、图3（e）、图3（f）。

如图3所示，在3种器件模型中，费米能级附近不同自旋电子的塞贝克系数S↑(↓)均具有相反的符号，表示在外加温度梯度ΔT的情况下，器件中的不同自旋电子会向相反的方向流动，产生自旋流Is=(S↑G↑-S↓G↓)ΔT和电荷流Ic=(S↑G↑+S↓G↓)ΔT。为了简单起见，将自旋流因子表示为Fs=(S↑G↑-S↓G↓)，并将电荷电流因子表示为Fc=(S↑G↑+S↓G↓)。当同时满足Fc=0和Fs≠0时，意味着两种自旋状态的电子流向相反，数量相同，此时电荷流Ic为0，但是自旋流Is依然存在，即纯自旋流。图4是W1、W2和W3器件模型的自旋流因子Fs和电荷流因子Fc在温度T为100 K、200 K、300 K下的计算结果，图4（a）、图4（b）以及图4（c）的纵坐标是自旋流因子Fs，图4（d）、图4（e）以及图4（f）的纵坐标是电荷流因子Fc，横坐标均为器件的化学势。可以看出，在3种器件模型中，费米能级附近均存在一个特殊的能量点E0，在该能量点处，满足纯自旋流条件，即获得了纯自旋流。因此，可以通过外加门电压的方法将器件的化学势微调至E0，分别约为-0.01 eV、0.09 eV、0.06 eV，以获得纯自旋流。

图4 3种模型的电荷流因子和自旋流因子

3 结 论

本文提出了一种在锯齿形石墨烯纳米带的两个边缘外延出同样的等腰三角形来调控器件的输运性质以获得纯自旋流的方案。计算结果表明，不同自旋电子的透射谱谱在费米能级附近的呈现“X”形交叉，导致不同自旋电子的塞贝克系数在费米能级附近具有相反的符号，表示不同自旋的电子在温度场下朝相反方向流动，形成自旋流和电荷流。进一步的研究发现，不同自旋通道的塞贝克系数不仅随着引入的反量子点数目的增加而增大，也随着温度的升高而增加，通过微调器件的化学势可以获得纯自旋流。