某直列四缸发动机悬置系统模态优化设计

王楷焱 任晓雪

摘要：本文针对某四缸发动机模态解耦率较差的问题，对发动机悬置系统模态进行优化设计。首先通过多体动力学软件，建立6自由度发动机悬置系统模型，对模型进行模态分析和计算。以悬置元件的刚度和位置参数为主要设计变量，悬置系统模态能量解耦率为优化目标，采用遗传算法对模型进行优化。优化后，发动机悬置系统的解耦水平有显著提高。

Abstract： Aiming at the problem of poor modal decoupling rate of a four cylinder engine， the modal optimization design of engine mounting system is carried out. Firstly， the model of 6-DOF engine mounting system is established by multi-body dynamics software. The modal analysis of the model is carried out. The stiffness and position parameters of the mounting elements are chosen as the main design variables， and the modal energy decoupling rate of the mounting system is taken as the optimization objective. After optimization， the decoupling level of engine mounting system is improved significantly.

關键词：发动机悬置;模态解耦;优化设计;遗传算法

Key words： engine mounting system;modal decoupling;optimization design;genetic algorithm

中图分类号：U464.1                                      文献标识码：A                                  文章编号：1674-957X（2021）09-0007-02

0  引言

21世纪后，我国的汽车技术进入了一个高速发展的时期，整个汽车行业对汽车的性能和品质得到更大的重视。汽车的NVH性能作为汽车品质的重要代表，得到了企业和科研人员的格外关注。汽车的主要振动噪声源有很多，包括：发动机、路面、气流、传动系统等。其中最为主要的振动噪声源就是发动机。发动机的振动噪声一般可以通过整车声学包、整车隔声、隔振的方式进行控制。在这些手段中，最为重要的就是通过发动机悬置系统进行控制。

发动动机悬置是一种连接发动机和车身/副车架的弹性元件，常用的类型包括液压悬置和橡胶悬置。整车一般采用三到四个悬置元件组成悬置系统，形成对发动机和变速器的支撑。悬置系统最主要的作用除了支撑发动机外，就是对发动机产生的振动进行隔离，减少传递到车内的振动，提高整车的NVH水平[1]。

悬置系统模态解耦水平的优劣，会影响到发动机悬置系统的隔振效果。模态解耦率低，会导致发动机工作时产生振动耦合的现象，加剧发动机的振动[2]。对悬置系统模态的分析和优化，一般多基于多体动力学软件或者Matlab软件分析[3-4]。本文主要通过多体动力学软件ADAMS对悬置系统建模，并进行模态分析计算。通过联合仿真优化的方式，采用遗传算法对模型的模态进行优化。

1  悬置系统模态理论

设6自由度动力总成悬置系统的质量为m，悬置位移为q，根据拉格朗日方程可以得到系统的振动方程为：

（1）

式中，M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为悬置受力矩阵。

对式（1）进行微分方程的求解，可以得到悬置系统的各阶模态频率ωi，以及各阶模态的振型φi。

各阶模态能量占比可以表示为[5]。

（2）

式中，mkl为质量矩阵M中的元素。当某阶模态的模态能量占比较大时，说明该阶模态的能量集中。

2  发动机悬置系统建模仿真

2.1 动力总成的建模

由于动力总成（发动机，变速器，离合器，发动机附件）自身模态频率相对于动力总成悬置系统的模态频率高很多，因此在研究过程中将动力总成简化为刚体，用质量单元模拟，忽略发动机液体部分的质量影响，根据动力总成的试验测得的质量和惯量参数，对质量单元进行设置。

2.2 悬置元件的建模

动力总成悬置元件通常采用橡胶悬置元件或橡胶液压悬置元件，其特点是能够在横向、纵向和垂向对动力总成进行有效支撑，并对其振动进行衰减。因此在建模过程中考虑到悬置元件的这一特性，采用弹簧阻尼单元“bushing”对其进行拟合，以保证模型动态仿真的准确性，建立“bushing”后，在模型中对悬置元件的刚度和阻尼参数进行设置。

2.3 仿真分析

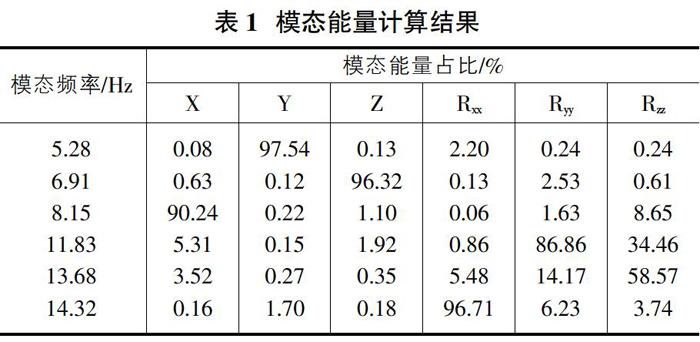
对悬置系统模型进行模态计算，结果如表1所示。

仿真结果表明该动力总成悬置系统的Y、Z、Rxx，三个方面的模态能量解耦集中度好，分别达到了97.54%、96.32%和96.71%，而X、Ryy、Rzz三个方向的解耦较差，其中Rzz还不到60%，即在这三个频率下，悬置系统容易产生振动耦合问题，因此，需要对这三个模态的能量解耦率进行重点优化。

3  悬置系统优化设计

3.1 优化目标及设计变量

根据仿真结果，优化目标选择悬置系统各阶模态的主振动方向的模态能量占比为优化目标，将各阶模态的能量解耦率不能低于90%，各阶模态的模态频率间隔大于等于1Hz设置为优化约束条件。

悬置系统的设计变量是悬置系统可优化的参数，通常包括了悬置元件的安装位置参数、悬置元件的刚度参数和悬置元件的阻尼参数等等。但是，阻尼参数一般对悬置系统的模态的影响非常小，所以不作为优化变量进行设置。这里，选择悬置系统的位置参数，包括：左悬置X向、Y向、Z向安装位置，右悬置X向、Y向、Z向位置参数，以及扭力杆X向、Y向、Z向悬置安装位作为优化变量。同时悬置系统的刚度参数，包括：左悬置X向，Y向，Z向刚度、右悬置X向、Y向、Z向刚度、以及扭力杆悬置X向、Y向、Z向刚度，作为优化变量。悬置的刚度和位置变量的变化范围为上下20%。

3.2 仿真优化原理

模型优化流程如图1所示。首先，在ADAMS中将悬置元件的刚度和坐标点参数化处理，形成设计变量。通过相应的接口，实现ADAMS软件和Matlab的数据交互。在Matlab软件中建立遗传算法程序，以悬置的位置和刚度作为算法中的个体，初值种群数为200，通过ADAMS软件进行仿真分析，将优化目标反馈到Matlab中，Matlab对优化目标进行判断，如果不满足要求，则将种群进行交叉和变异，产生新种群后继续进行仿真分析，直到满足优化要求。

3.3 优化结果分析

优化结果，如表2所示。优化结果表明悬置系统的X、Ryy、Rzz的模态能量集中度均有所提高，其中Rzz方向提高的幅度最大，提高了157.2%，优化后主振型模态能量占比达到92.06%，Ryy方向也提高了13.3%，优化后主振型模态能量占比达到98.49%。证明了优化的有效性。

4  结论

本文采用ADAMS软件，建立了发动机悬置系统的多体动力学模型，对模型进行了模态分析。分析结果表明该悬置系统的X、Ryy、Rzz三个方向的模态解耦率较差，会产生模态耦合问题。通过ADAMS与Matlab软件联合仿真优化，以悬置元件的刚度参数和位置参数为优化变量，以悬置主振型模态能量占比最大为优化目标，应用遗传算法，对模型进行了优化，优化结果表明X、Ryy、Rzz三个方向的模态能量集中度均得到了有效提高，满足了设计要求。

参考文献：

[1]杨守财.基于灵敏度分析的发动机悬置系统稳健优化设计[J].内燃机与配件，2021（02）：5-6.

[2]徐建珂，张贺广.基于ADAMS软件的发动机悬置系统优化设计[J].橡胶科技，2020，18（10）：586-588.

[3]宗德媛，朱炯，张志军，仇培涛.发动机悬置系统动力学仿真与模态试验验证[J].建筑机械，2019（02）：76-80，4.

[4]陶庆水，张亚新，钟海兵，刘建勋，朱石沙.某國产SUV悬置系统优化设计与隔振测试评价[J].噪声与振动控制，2016，36（02）：112-115，204.

[5]杨金元，李福斌，陈树勋.发动机动力总成悬置系统模态分析与优化[J].装备制造技术，2014（02）：16-19.

基金项目：辽宁省自然科学基金指导计划项目（20180550710）; 中国博士后科学基金资助项目（2019M651147）;辽宁省博士科研启动基金资助项目（2020-BS-156）。

作者简介：王楷焱（1983-），男，辽宁沈阳人，副教授，博士，主要从事汽车系统动力学与控制方面的研究。