间接激励压电发电机的建模仿真与试验研究
王淑云 朱雅娜 阚君武 张忠华 黄鑫 侯刘奖


摘要: 为满足旋转机械监测系统的自供电需求、解决现有压电发电机可靠性低及有效带宽窄等问题,提出一种基于移动凸轮间接激励并限幅的旋转式压电发电机(简称间接激励压电发电机)。介绍了发电机的结构原理并进行了建模仿真与试验测试,获得了激励磁铁数量比、凸轮升程及升角对激振力形式/幅值、压电振子变形量/输出电压及发电机带宽等的影响规律。结果表明:利用凸轮间接激励可有效地限制压电振子的振幅/输出电压、避免幅频特性曲线出现明显的谐振峰;其他条件相同时,使压电振子变形量/输出电压相同的有效带宽随激励磁铁数量比的减小及凸轮升角(30°?45° 范围内)的增加而增加;隨凸轮升程的增加,压电振子变形量/输出电压增加、有效带宽减小;磁铁数量比为0.25、升角为40°、升程为2/ 3/ 4/ 5 mm时,使输出电压为20/ 40/ 60/ 70 V的有效转速范围为212.8/ 67.2/ 67.2/ 44.8 r/min;此外,存在最佳负载70 kΩ使发电机输出功率最大(9.66 mW)。
关键词: 旋磁; 压电发电机; 间接激励; 凸轮; 限幅
中图分类号: TN384; TM619 文献标志码: A 文章编号: 1004-4523(2021)01-0127-07
DOI:10.16385/j.cnki.issn.1004-4523.2021.01.014
引 言
为满足无线传感器/医学植入系统/结构健康与环境监测系统/便携式电子产品等微功率设备实时供电的需求、减少废弃化学电池处理所造成的资源浪费与环境污染等问题,基于环境能量回收的压电发电机(亦称压电俘能器)研究已成为国内外的热点[1?3]。根据环境能源形式的不同,现已开发的压电发电机可分为振动式[4?5]、流体激励式(风能与液体流动能量)[6?8]及旋转式[9]等,每类压电发电机都有其自身的特点及适用领域。
压电旋转发电机主要通过收集旋转体(轴/轮、轴承、螺旋桨/风力发电机叶片等)动能发电并构造自供电监测系统。根据压电振子的激励方式,现有压电旋转发电机可分为两大类:①接触激励发电机,通过接触力(撞击力[10]或拨动力[11])迫使压电振子变形发电,其优点是激励可靠,但间歇式的接触?脱离工作模式下会产生接触冲击与噪音,故仅适于低速环境(200 r/min[11]);②非接触激励发电机,通过非接触力(压电振子附加质量的惯性力[12?13]或相对转动的磁耦合力[14?15])迫使压电振子变形发电,其优点是结构简单、无接触冲击和噪音,但有效带宽窄、可靠性低?惯性激励发电机也仅适于低速环境,高速时压电振子会因惯性力过大无法产生往复弯曲变形或单向变形过大而损毁;旋磁激励适于高速环境,但仅当发电机可激励频率为压电振子分频/倍频时发电能力较强,压电振子共振与非共振时其输出电压之比高达数倍(7.5倍)[16]或数十倍(67倍)[17],共振时压电片易因应力过大而损毁。
为提高旋转发电机的可靠性、转速适应性及有效频带宽度(有效的转速范围),Guo 等[18]及Zhang 等[19]等研究了磁力耦合式非线性自激发电机,Zou 等[20]研究了基于磁力耦合的双振子自激发电机,Nasrin等[21]和Xie等[22]研究了双稳态旋磁激励发电机,阚君武等研究了磁力夹持调频[17]及变刚度调频的旋磁激励发电机[23]。上述发电机在可靠性、有效带宽及转速适应性等方面都有一定程度的改善,但依然利用压电振子共振时的双向弯曲变形发电(脆性压电片的许用拉应力远低于许用压应力),其幅频特性曲线依然存在非常明显的谐振峰,故可靠性、转速适应性及有效频带宽度(发电机系统固有频率可调性)仍有待进一步提升。
提出了一种将接触激励和非接触激励相结合的间接激励压电发电机,先利用旋转磁铁使移动凸轮往复振动(非接触激励),再利用移动凸轮激励压电振子(接触激励)。该方案可通过磁耦合激振力和弹簧刚度调节凸轮的幅频特性曲线(获得所需的非共振振幅和谐振频率)、通过凸轮升程/升角控制压电振子的幅频特性(使压电振子产生幅值适当、平缓/无明显谐振峰的单向弯曲变形),进而提高发电机的可靠性、有效频带宽度和转速适应性。从理论和试验两方面展开研究,着重探讨激励磁铁数量比、凸轮升程及凸轮升角对激振力形式/幅值、凸轮及压电振子幅频响应特性及发电机有效带宽等的影响规律,证明间接激励压电发电机结构原理的可行性。
1 压电发电机的结构与工作原理
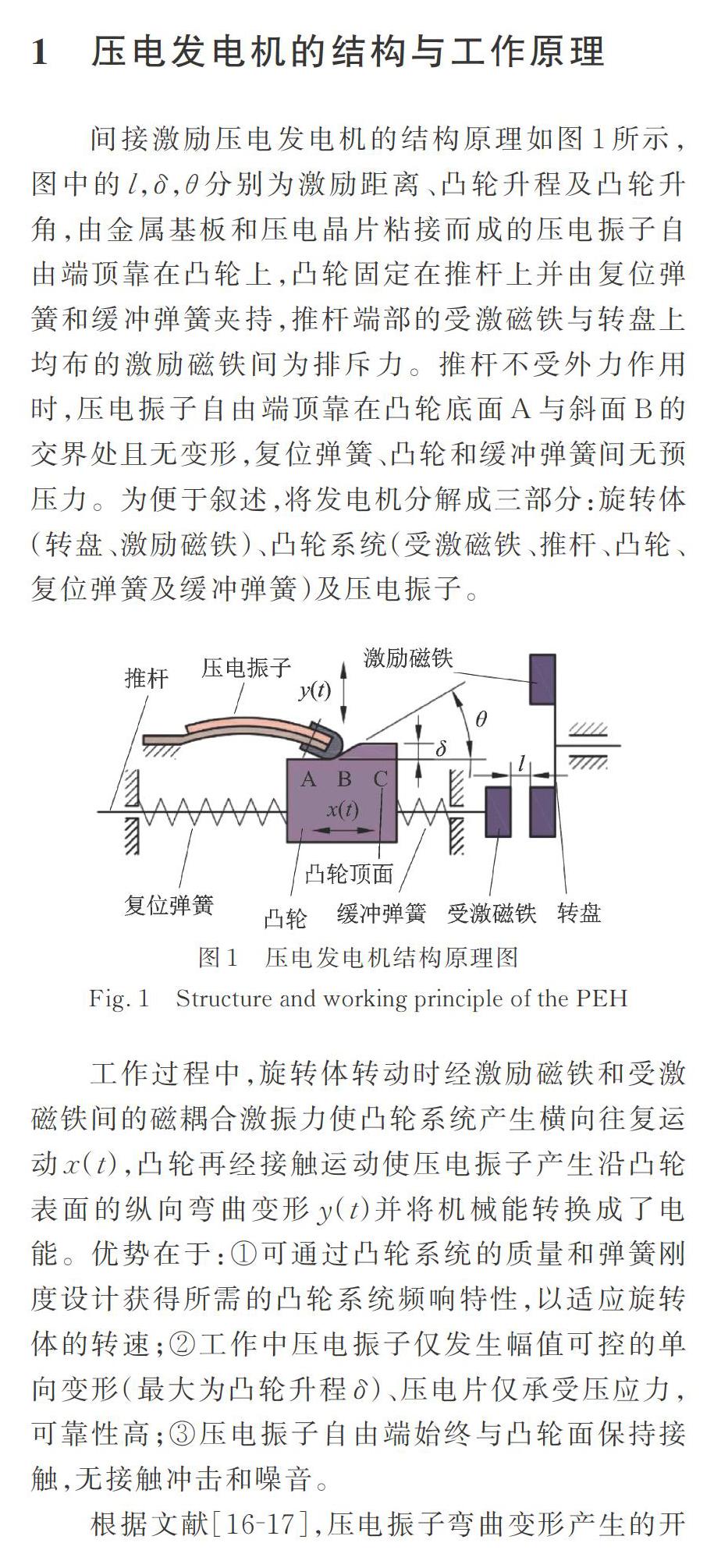
间接激励压电发电机的结构原理如图1所示,图中的分别为激励距离、凸轮升程及凸轮升角,由金属基板和压电晶片粘接而成的压电振子自由端顶靠在凸轮上,凸轮固定在推杆上并由复位弹簧和缓冲弹簧夹持,推杆端部的受激磁铁与转盘上均布的激励磁铁间为排斥力。推杆不受外力作用时,压电振子自由端顶靠在凸轮底面A与斜面B的交界处且无变形,复位弹簧、凸轮和缓冲弹簧间无预压力。为便于叙述,将发电机分解成三部分:旋转体(转盘、激励磁铁)、凸轮系统(受激磁铁、推杆、凸轮、复位弹簧及缓冲弹簧)及压电振子。
工作过程中,旋转体转动时经激励磁铁和受激磁铁间的磁耦合激振力使凸轮系统产生横向往复运动x(t),凸轮再经接触运动使压电振子产生沿凸轮表面的纵向弯曲变形y(t)并将机械能转换成了电能。优势在于:①可通过凸轮系统的质量和弹簧刚度设计获得所需的凸轮系统频响特性,以适应旋转体的转速;②工作中压电振子仅发生幅值可控的单向变形(最大为凸轮升程![]() )、压电片仅承受压应力,可靠性高;③压电振子自由端始终与凸轮面保持接触,无接触冲击和噪音。
)、压电片仅承受压应力,可靠性高;③压电振子自由端始终与凸轮面保持接触,无接触冲击和噪音。
显然,间接激励发电机的输出性能是由压电振子结构尺寸/参数、激励磁铁数量/结构参数、受激磁铁结构参数、凸轮升程/升角/质量、复位弹簧与缓冲弹簧刚度及激励距离等诸多参数共同决定的。本文着重研究激励磁铁数量及凸轮结构尺度对激振力形式/幅值、凸轮系统动态特性及压电振子输出特性的影响规律。
2 发电机的理论建模与仿真分析
2.1 动力学模型的建立
由图1可知,当压电振子自由端始终与凸轮表面接触时,压电振子变形特性完全由凸轮系统结构参数及幅频特性决定。不计压电振子自身的质量及压电振子与凸轮间的滑动摩擦力时,凸轮的动力学微分方程可表示为
为获得凸轮系统的响应函数,首先需要确定激振力F(t),它是由激励磁铁和受激磁铁结构及位置关系等共同决定的,难以通过解析的方法获得。本文将通过有限元仿真研究激励磁铁数量比(α = n0 / N,n0和N分别为激励磁铁数和转盘上最多可布置的磁铁数)对激振力的影响规律。如图2所示,激励磁铁与受激磁铁间的耦合作用力可分解为轴向力Fa和径向力Ft,其中的径向力Ft通过改变推杆运动的摩擦力影响驱动力,可忽略不计,故凸轮所受的激振力F(t)即为轴向力Fa。仿真中所用的相关参数为:激励磁铁回转半径R = 46 mm,激励磁铁与受激磁铁的半径r = 10 mm,激励磁铁和受激磁铁的厚度分别为4 mm和8 mm,N = 12,l = 1 mm。
圖3和4分别给出了磁铁数量比α对激振力波形及其幅值的影响规律曲线,并定义排斥力为正。图中曲线表明,磁铁数量比α对激振力形式及其幅值都有较大影响:随着α增加,激振力形式由一般性周期激励逐渐转变为非对称的简谐激励;激振力的偏置量随α增加而增加,存在一个最佳的磁铁数量比(α≈0.6)使激振力幅值Fm=Fd -Fx最大,其中Fd 和Fx分别为激振力的极大值和极小值。产生上述现象的原因在于,α较小时各激励磁铁的激振力相互独立,而α较大时激励磁铁间的作用力具有耦合性,从而改变激振力的形式和幅值。上述仿真结果表明,虽然激振力形式及幅值随α的变化而变化,但力的波形都近似为半正弦波,由此可获得凸轮所受的激振力及其振动响应函数[16]:
3 试验测试与分析
为验证间接激励发电机原理的可行性及仿真结果的正确性,设计制作了如图9所示的试验样机和测试系统。试验设备包括:电机(额定转速2850 r/min)、DS5042M型数字存储示波器和变频器(变频范围0?50 Hz)等。试验所用器件的结构参数为:激励磁铁与受激磁铁尺寸均为Φ20 mm×4 mm,商用预弯压电振子的尺寸为(40×40×0.5) mm3、预弯半径300 mm,k1 =k2 = 50 N/m, l = 8 mm。通过Comsol仿真软件测得压电振子刚度约为350 N/m,压电振子共振频率远大于凸轮系统的激励频率,故其变形特性完全由凸轮系统结构参数及频率特性决定。变频器控制电机转速的最低启动转速为60 r/min。单因素试验中所用的固定参数为α= 0.25,δ= 2 mm,θ= 40°,输出电压均为开路电压。
图10为α不同时Vg ?n关系曲线。图中曲线表明,确实存在多个最佳转速使输出电压Vg出现峰值,最佳转速段的数量与α有关,但各最佳转速段所对应的峰值电压 Vg*受α的影响不大。α= 0.25/ 0.33/ 0.5/ 0.67时的最佳转速段数量及其所对应的峰值电压Vg*分别为2/ 2/ 1/ 1和41.6/ 40.8/ 40.8/ 37.6 V,使输出电压Vg = 20 V的有效转速带宽为![]() = 212.8/ 268.8/ 168/ 78.4 r/min。这与图5和6所示的仿真结果基本一致,证明凸轮间接激励具有明显的限幅作用。与图6所示的仿真曲线不同,图10的试验曲线上并无完全水平部分,这是因为实际工作中压电振子端部沿凸轮表面运动时未能完全贴合,存在随机脱离与跳起现象。
= 212.8/ 268.8/ 168/ 78.4 r/min。这与图5和6所示的仿真结果基本一致,证明凸轮间接激励具有明显的限幅作用。与图6所示的仿真曲线不同,图10的试验曲线上并无完全水平部分,这是因为实际工作中压电振子端部沿凸轮表面运动时未能完全贴合,存在随机脱离与跳起现象。
图11和12分别为δ和θ不同时的Vg ?n关系曲线。图中曲线表明,其他条件确定时,发电机的输出电压Vg及其有效带宽确实均与δ和θ有关:①δ增大时Vg*增加、所对应的有效带宽减小;δ= 2/ 3/ 4/ 5 mm时Vg* = 41.6/ 54.8/ 68.8/ 80.2 V,输出电压Vg = 20/ 40/ 60/ 70 V所对应的有效转速带宽为![]() = 212.8/67.2/67.2/44.8 r/min;②θ较小(30°?45°)时,最大输出电压Vg*受θ的影响不大,但其所对应的有效转速带宽随θ增加有所增加;θ较大(≥50°)时最大输出电压Vg*有所下降,带宽随θ有所增加;θ= 30° /35°/ 40°/ 45°/ 50°时,Vg = 20 V所对应的转速带宽为
= 212.8/67.2/67.2/44.8 r/min;②θ较小(30°?45°)时,最大输出电压Vg*受θ的影响不大,但其所对应的有效转速带宽随θ增加有所增加;θ较大(≥50°)时最大输出电压Vg*有所下降,带宽随θ有所增加;θ= 30° /35°/ 40°/ 45°/ 50°时,Vg = 20 V所对应的转速带宽为![]() = 212.8/ 201.6/ 212.8/ 246.4/ 168 r/min。θ= 50°时Vg*下降的原因可能是凸轮出现了自锁,压电振子端部不能沿凸轮表面顺利地往复运动。故应在凸轮不自锁的情况下选用较大的升角,以减小所需的凸轮横向振幅, 且凸轮升程不宜过小,升程为零时压电振子无变形。图11和12所示的试验测试结果与前文仿真分析的结论较为一致,再次证明通过凸轮间接激励可有效地限制压电振子变形量。实际应用中可根据具体的需要,通过凸轮系统参数及激励磁铁数量比调节凸轮系统的幅频特性及压电振子的振动特性,使发电机在较宽转速域内输出稳定的电压。
= 212.8/ 201.6/ 212.8/ 246.4/ 168 r/min。θ= 50°时Vg*下降的原因可能是凸轮出现了自锁,压电振子端部不能沿凸轮表面顺利地往复运动。故应在凸轮不自锁的情况下选用较大的升角,以减小所需的凸轮横向振幅, 且凸轮升程不宜过小,升程为零时压电振子无变形。图11和12所示的试验测试结果与前文仿真分析的结论较为一致,再次证明通过凸轮间接激励可有效地限制压电振子变形量。实际应用中可根据具体的需要,通过凸轮系统参数及激励磁铁数量比调节凸轮系统的幅频特性及压电振子的振动特性,使发电机在较宽转速域内输出稳定的电压。
图13为转盘转速n不同时输出功率Pg与负载电阻Rl的关系曲线。功率测试中,压电振子与整流滤波电路和可调电阻器相连。由图中曲线可知,各转速下都存在較佳的电阻Rl使输出功率Pg最大,各转速所对应的最佳负载基本相同(70 kΩ),输出功率的最大值随转速增加而降低;试验转速为n =112 r/min时所获得的最大输出功率约为9.66 mW。
4 结 论
提出一种间接激励压电发电机,通过理论仿真与试验测试研究了激励磁铁数量比、凸轮升程、升角和转速等对其输出性能影响规律。结果表明,采用移动凸轮间接激励可有效避免发电机的电压?转速特性曲线出现明显的谐振峰,进而提高发电机的可靠性和有效转速带宽。具体结论如下:
(1)激励磁铁数量比对激振力作用形式、凸轮?弹簧系统的幅频特性及发电机的有效带宽均有较大影响。随激励磁铁数量比增加,激振力由一般性周期激励逐渐变为简谐激励,存在多个最佳转速使凸轮?弹簧系统共振,且最佳转速数量随激励磁铁数量比的增大而减小。
(2)凸轮横向振幅较大(![]() )时,凸轮对压电振子变形具有抑制功能,发电机输出电压及其有效带宽与激励磁铁数量比、凸轮升程及凸轮升角有关,其他条件相同时:使输出电压相同的有效带宽随激励磁铁数量比及凸轮升程的减小而增加,随凸轮升角(30°?45°)的减小而降低;最大输出电压随凸轮升程的增加而增加,受激励磁铁数量比及凸轮升角变化影响较小。磁铁数量比为0.25、升角为40°、升程为2/3/4/5 mm时,使输出电压为20/40/60/70 V所对应的有效转速范围为212.8/ 67.2/ 67.2/ 44.8 r/min。
)时,凸轮对压电振子变形具有抑制功能,发电机输出电压及其有效带宽与激励磁铁数量比、凸轮升程及凸轮升角有关,其他条件相同时:使输出电压相同的有效带宽随激励磁铁数量比及凸轮升程的减小而增加,随凸轮升角(30°?45°)的减小而降低;最大输出电压随凸轮升程的增加而增加,受激励磁铁数量比及凸轮升角变化影响较小。磁铁数量比为0.25、升角为40°、升程为2/3/4/5 mm时,使输出电压为20/40/60/70 V所对应的有效转速范围为212.8/ 67.2/ 67.2/ 44.8 r/min。
(3)存在最佳负载电阻使输出功率最大,且最佳负载受转速影响较小。转速为112 r/min、最佳负载电阻为70 kΩ时,试验所获得的最大输出功率约为9.66 mW。
参考文献:
[1] Siddique A R M, Mahmud S, Heyst B V. A comprehensive review on vibration based micro power generators using electromagnetic and piezoelectric transducer mechanisms[J]. Energy Conversion & Management, 2015, 106: 728-747.
[2] Ferdous R M, Reza A W, Siddiqui M F, Renewable energy harvesting for wireless sensors using passive RFID tag technology: A review[J]. Renewable & Sustainable Energy Reviews, 2016, 58: 1114-1128.
[3] Wei C, Jing X. A comprehensive review on vibration energy harvesting: Modelling and realization[J]. Renewable and Sustainable Energy Reviews, 2017, 74: 1-18.
[4] Yan C, Zhang Q, Yao M, et al. Vibration piezoelectric energy harvester with multi-beam[J]. AIP Advances, 2015, 5(4): 4495-4498.
[5] Rathinamala S, Manoharan S. Vibration powered generators and power processing circuits for energy harvesting: A survey[J]. International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, 2014, 3(5): 9597-9564.
[6] Li S, Yuan J, Lipson H. Ambient wind energy harvesting using cross-flow fluttering[J]. Journal of Applied Physics, 2011, 109(2): 026104.
[7] 王淑云,富佳偉,阚君武,等. 一种脱涡纵振式压电管道气流发电机[J]. 机械工程学报,2019, 55(8): 24-29.
Wang S, Fu J, Kan J, et al. A pipe airflows piezoelectric energy harvester with longitudinal vibration excited by vortex shedding[J]. Journal of Mechanical Engineering, 2019, 55(8): 24-29.
[8] Kan J, Fan C, Wang S, et al. Study on a piezo-windmill for energy harvesting[J]. Renewable Energy,2016, 97: 210-217.
[9] Gu L, Livermore C. Compact passively self-tuning energy harvesting for rotating applications[J]. Smart Mater Structures, 2012, 21(1): 015002.
[10] Yang Y, Shen Q, Jin J, et al. Rotational piezoelectric wind energy harvesting using impact-induced resonance[J]. Applied Physics Letters, 2014, 105(5): 053901.
[11] Janphuang P, Lockhart R A, Isarakorn D,et al. Harvesting energy from a rotating gear using an AFM-like MEMS piezoelectric frequency up-converting energy harvester[J]. Journal of Microelectromechanical Systems, 2015, 24(3): 742-754.
[12] Zhang Yunshun, Zheng Rencheng, Shimono Keisuke S, et al. Effectiveness testing of a piezoelectric energy harvester for an automobile wheel using stochastic resonance[J]. Sensors, 2016, 16(10): 1727.
[13] Febbo M, Machado S P, Gatti C D, et al. An out-of-plane rotational energy harvesting system for low frequency environments[J]. Energy Conversion & Management, 2017, 152: 166-175.
[14] Kan J, Fu J, Wang S, et al. Study on a piezo-disk energy harvester excited by rotary magnets[J]. Energy,2017, 122: 62-69.
[15] Wu W H, Kuo K C, Lin Y H, et al. Non-contact magnetic cantilever-type piezoelectric energy harvester for rotational mechanism[J]. Microelectronic Engineering, 2018, 191: 16-19.
[16] 阚君武,于 丽,王淑云,等. 旋磁激励式压电悬臂梁发电机性能分析与试验[J]. 机械工程学报,2014, 50(8): 144-149.
Kan J, Yu L, Wang S, et al. Performance analysis and test of piezo-cantilever generator excited by rotary magnet[J]. Journal of Mechanical Engineering, 2014, 50(8): 144-149.
[17] 阚君武,文 欢,王淑云,等. 磁铁夹持式压电俘能器输出性能分析与试验[J].振动工程学报,2019, 32(1): 80-86.
Kan J, Wen H, Wang S, et al. Performance analysis and test of a piezoelectric energy harvester based on magnets holding[J]. Journal of Vibration Engineering, 2019, 32(1): 80-86.
[18] Guo B, Chen Z, Cheng C, et al. Characteristics of a nonlinear rotating piezoelectric energy harvester under variable rotating speeds[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 47: 411-423.
[19] Zhang Y, Zheng R, Nakano K, et al. Stabilising high energy orbit oscillations by the utilisation of centrifugal effects for rotating-tyre-induced energy harvesting[J]. Applied Physics Letters, 2018,112(14): 143901.
[20] Zou H X, Zhang W M, Li W B, et al. Design and experimental investigation of a magnetically coupled vibration energy harvester using two inverted piezoelectric cantilever beams for rotational motion[J]. Energy Conversion and Management, 2017, 148: 1391?1398.
[21] Nasrin R H, Ahmadreza T, Rasoul D. A topology and design optimization method for wideband piezoelectric wind energy harvesters[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2165-2173.
[22] Xie Z, Xiong J, Zhang D, et al. Design and experimental investigation of a piezoelectric rotation energy harvester using bistable and frequency up-conversion mechanisms[J]. Applied Sciences, 2018, 8(9): 1418.
[23] 阚君武,何恒钱,王淑云,等. 可调频旋磁激励式压电发电机的设计与试验[J]. 光学精密工程,2019, 27(3): 577-583.
Kan J, He H, Wang S, et al. Structure and performance of rotating piezoelectric generator with tunable frequency[J]. Optics and Precision Engineering, 2019, 27(3): 577-583.
Abstract: To meet the demands of self-powered monitoring system for rotating machine and improve the reliability and effective working frequency band for existing piezoelectric energy harvesters, a Rotary Piezoelectric Energy Harvester (PEH) is introduced, which is based on a moving cam with indirect and limited excitation. The system structure and working principle of the energy harvester are introduced and its dynamic response model is established. In this way, the influence of the excitation magnets ratio, the cam lift and angle to the excitation force form/magnitude, the deformation of the piezoelectric vibrator/output voltage and the harvester bandwidth are obtained by simulation and experiment. The research results show that the indirect excitation of the cam can effectively limit the amplitude/output voltage and avoid the obvious resonance peak of the amplitude-frequency characteristic curve; When other conditions are given, the effective bandwidth of the piezoelectric vibrator deformation/output voltage increases as the excitation magnet ratio decreases and the cam angle increases (30°-45°). As the cam lift increases, the piezoelectric vibrator deformation amount/output voltage increases, and the effective bandwidth decreases. When magnet ratio is 0.25,lift angle is 40°,excitation distance are 2/3/4/5mm, the effective speed range is 212.8/67.2/67.2/44.8 r/min for the output voltage is 20/40/60/70 V; In addition, there is an optimal load of 70 kΩ to maximize harvester output power (9.66 mW).
Key words: rotating magnets; piezoelectric energy harvester; indirect excitation; cam; amplitude limit
作者簡介: 王淑云(1965-),女,教授,硕士生导师。E-mail:jutwsy@163.com
通讯作者: 阚君武(1965-),男,教授,博士生导师。电话:13958480260;E-mail:kjw@zjnu.edu.cn

