低温高压自密封球阀研究设计

何 俊 韩龙生 彭成武 李华祖 庞 媛 李 超 宋鹏飞

(湖北泰和石化设备有限公司 宜昌 443000)

1 引言

随着低温环境应用技术的发展,低温流体得到越来越广泛的应用,例如液氮被广泛地应用于工业生产、科研领域、医疗卫生等,液氮和液氧作为火箭推进剂在国防领域表现出显著优点[1]。另外,近年来,随着能源紧缺,液化天然气也成为主要能源之一,液化天然气具有清洁、高效的特点,越来越受到社会青睐,很多国家都将LNG 列为首选燃料,天然气在能源供应中的比例迅速增加。

低温阀门在液化天然气(LNG)接收站中有着广泛的应用,主要用来控制管道介质的截断或连通,由于LNG 具有易燃、易爆和低温等特点,其密封性能直接关系到LNG 管道系统的运行安全[2]。而根据《中国“十三五”规划》指出大力发展相关产业,逐步把天然气、太阳能光热培育成主体能源之一,力争使这两大能源消费比重翻番。在此背景下,国内阀门行业必须打破现有格局,进军高端阀门领域成为当下行业发展的必然趋势。尤其是大口径高磅级低温球阀,此类球阀产品的核心技术长期被外国厂家垄断,国内大口径高磅级球阀基本都是依赖进口。在面对制造技术强大的欧美发达国家,国内阀门行业处于发展不成熟、技术落后。阀门生产企业大多采取在原有产品上稍作改进或者模仿国外同类产品的方式,独立自主创新不够[3],因此缺少具有自主知识产品的核心技术和具有国际竞争力的高端产品。国内低温阀门高端产品的市场需求和前景巨大,市场对低温阀门高端产品的期望也是空前的,只有不断实现产品的创新,提高低温阀门的技术质量,才能有效填补国内空白,在低温阀门市场占领制高点,实现国产化的发展需求。

在此基础上,通过对液化天然气作业要求的分析及大口径高压球阀不足之处的研究,设计出一种中道自密封球阀结构形式,对其密封结构做出改进,使密封性能更为安全可靠,并对核心受力部件进行力学计算,防止零部件受力损坏,采用有限元分析方法来验证计算结果的正确性。

2 结构特点介绍

球阀阀体阀盖一般通过螺栓连接,由中道螺栓提供预紧力,不仅要抵挡中道产生的介质压力,还要提供密封所需的压力。在高压环境中,仅靠螺栓预紧难以满足设计需要,特别是当设计压力达到25 MPa 及以上时,不但要考虑材料在低温-196 ℃环境中的性能改变,还需应对球阀中腔液体介质汽化的可能,汽化后压力会骤增,单单依靠螺栓的力学性能,具有一定的隐患。

考虑到高压环境的安全性及低温工况的特殊性,提出一种高压低温环境下自密封球阀的结构,对其原理及可靠性进行了分析,并进行仿真验证校核,力求优化高压低温大口径球阀结构,打破国外垄断局面。

如图1 所示,为所设计自密封结构,包括阀体、阀盖、阀杆、球体盖、盘根、四开环、金属环、密封圈等,其特征在于:球体上方设有球体盖,球体与球体盖之间设有自润滑轴承;球体盖下端外部有一斜面结构,与密封圈、金属环紧密贴合;金属环由一四开环限位,四开环由挡块限位;挡块上方装有盘根密封,盘根紧配于阀体和球体盖之间。

图1 中腔自密封详细结构Fig.1 Detailed structure of cavity self sealing

相对于常规的中道结构,阀体阀盖之间采用螺栓连接,阀体中腔介质压力都由螺栓承受。图1 所示这种自密封形式,介质压力作用于球体盖上,再传递到四开环,压力主要作用于四开环,中道螺栓只需提供必需的密封力即可。不仅安全性极大的提高,且中腔压力越高,密封效果越好。该中腔自密封结构设计了三道密封形式,第一道为唇式密封,自带补偿作用;第二道密封为硬密封,在介质压力的作用下,金属环产生轻微变形,并产生一定的挤压力,密封住球体盖和阀体之间的间隙;第三道密封为石墨盘根密封,由中道螺栓提供密封预紧力。三道密封结构,极大的保证了密封性能,且第二道密封为自密封结构,压力越大,密封效果越好,适用于高磅级球阀。

中腔第二道密封形式需要密封住金属环、球体盖和阀体之间的间隙,其主要密封原理为:螺栓提升球体盖,使球体盖与金属环之间有一个初始预紧密封力,然后在介质压力作用下,球体盖产生向上的运动趋势,挤压金属环内圈锥面密封面,实现金属环和球体盖之间的密封,当介质压力达到足够高,金属环会产生一定的形变,金属环的外圈挤压向阀体,密封住金属环和阀体之间的间隙。作用于金属环上的力传递到四开环上,四开环镶嵌于阀体中,其实质是介质力大部分作用于四开环,不需中道螺栓来承担。不仅减轻了螺栓的负担,还可极大的减少中法兰的尺寸,节约成本。

3 可靠性计算

这种中腔自密封结构球阀,可以满足不同工况的作业需求。当介质压力不高时,第一、三道密封形式就足以满足密封性能的要求,当介质压力较大时,第二道自密封结构形式得以实现,提高了高压工况下的密封性能和安全性。该结构难点在于第二道密封形式的实现,需要介质提供的力可以满足金属对金属的硬密封要求,因此要计算其硬密封处的密封比压,以验算是否符合密封条件。同时,还要对主要承力部件金属密封环、四开环等进行力学计算,以验算这些受力件的强度是否可靠。

将中道几个主要受力部件结构简化为图2 所示物理模型,进行可靠性分析,其中A表示球体盖,B表示金属密封环,C表示四开环。B部件不仅需要封住与A 部件之间的锥面,还需封住与阀体之间的柱面间隙,即要求ab、cd密封面上有足够的密封比压,以阻挡介质逸出。

图2 简化物理模型Fig.2 Simplified physical model

3.1 密封性能计算

由于螺栓提供的初始预紧力相对于介质力来说小得多,在此忽略不计。首先对金属密封环的密封性能进行计算,即计算图2 中B部件ab、cd两个面的密封比压。A部件受到介质压力P的作用,其受力F为:

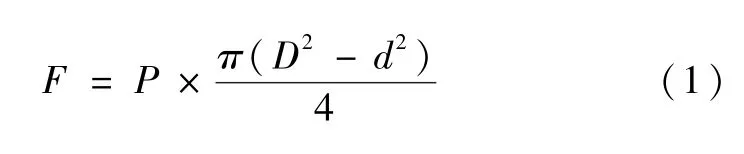
式中:D为A部件外径,mm;d为A部件内径,mm;P为介质压强,MPa。

A部件在介质压力的作用下,与B部件在锥面ab形成挤压,计算ab处的挤压应力,与密封必需比压和许用挤压强度进行对比,验算其强度和密封性能。简化计算过程,可得:

式中:D1为B部件密封斜面内径,mm;D2为B部件密封斜面外径,mm;α为B部件斜面与竖直方向的夹角,°;h1为B部件斜面高度,mm;σab为A、B部件接触锥面处的挤压强度,MPa。

B部件与阀体之间的环形空间的挤压应力为:

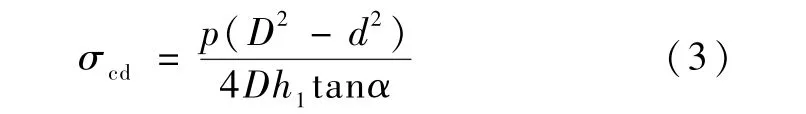
式中:σcd为B部件与阀体环形接触斜面的挤压强度,MPa。

B部件与阀体和A部件间的密封都属于硬密封,根据硬密封必需比压的经验算法,其必需密封比压为:

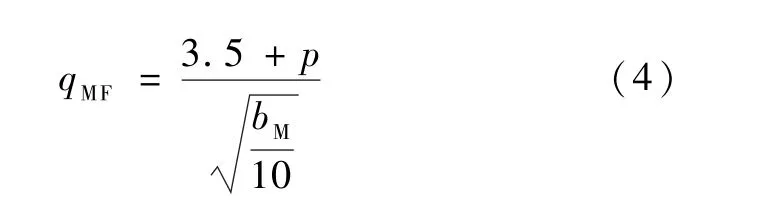
式中:qMF为密封必需比压,MPa;bM为密封面宽度,mm。

根据式(4)即可计算出ab面、cd面的必须密封比压qMF1、qMF2,需所计算挤压应力σab、σcd满足qMF1＜σab＜[σc],qMF2＜σcd＜[σc],[σc]为材料许用挤压应力。

在实际设计过程中,为了B部件可以更好的装配进入阀体中,B部件与阀体之间为间隙配合,因此式(2)、式(3)的计算值会比实际偏大。在实际工况当中,B部件在介质力的作用下产生轻微形变,弥补与阀体之间的间隙,产生一定的挤压,达到密封作用。

3.2 零部件可靠性分析

四开环C为最终主要承力件,需要对其强度进行计算,以防四开环C被破坏,导致结构失效。C部件的df面和de面为危险截面,对这两个截面的受力进行计算分析即可验证其强度。假设在力的传递过程中没有摩擦消耗等其他损失,由此计算的理论应力值会大于真实值,计算值偏大,相当于放了一定的安全系数,安全性更高。

计算得df面受到的挤压应力σdf为:

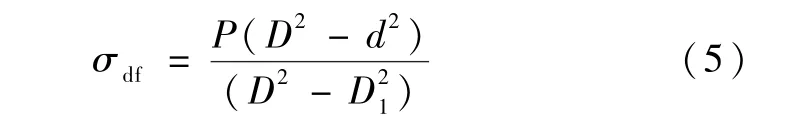
de面的剪切应力τde为:

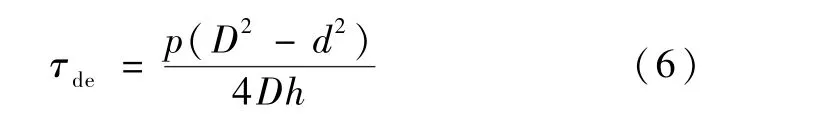
C部件可简化为外周固支受均布载荷的环形板,根据《化工容器设计》第三版可知,周边固支受均布载荷圆板的径向弯矩为:

式中:M为C部件截面所受弯矩,N·mm;μ为材料泊松比;q为圆板所受均布载荷,MPa。

如图3 所示,若将周边固支受均布载荷圆板中央挖去半径r部分圆板,留下一固支环形圆板,在其内周边作用着与取走部分圆板外圆柱面上大小相等,方向相反的弯矩与剪力。则C部件弯矩M′可由图4a、图4b、图4c 三个模型求得。

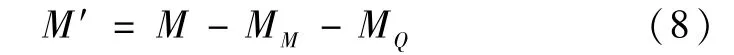
图3 周边固支圆板挖去半径r 部分圆板受力图Fig.3 Stress diagram for condition that a circular plate with radius r was removed from peripheral fixed circular plate

图4 外周固支环形板弯曲问题示意Fig.4 Bending diagram of annular plate with peripheral fixed support

MM和MQ分别为环形板受弯矩M1和剪力Q1引起的弯矩,其具体公式较为复杂,在此就不详细列举。由所得弯矩M′可求得外周固支均布载荷环形板径向最大应力为:

式中:K1为与环形板外径内径相关的系数,0.055;t为环形板厚度,mm。

由式(9)可计算出C部件所受最大应力,在环形板外径上下表面,即C部件直径D处。根据式(5)、式(6)和式(9)计算出C 部件危险截面的受力,再结合具体作业工况,及材料相应的力学性能等,与给定的相应许用应力进行比较,检验所设计零部件结构的安全性,确保所设计的结构具有足够的可靠性。

4 实例分析

为验证所推导计算公式的合理性,以12″25 MPa球阀为例,采用有限元数值模拟的方法来计算主要受力部件的应力,对理论计算值和数值模拟结果进行对比分析。零部件材质为ASTM A351 CF8M,初步设计出各部件尺寸。表1 中为所设计12″25 MPa 球阀中自密封结构相关尺寸数据,压力P取25 MPa。

表1 自密封结构相关尺寸Table 1 Dimensions of self sealing structure

简化模型,将各项参数载入Ansys 软件中,数值模拟自密封结构的受力情况,其结果如图5 所示。忽略当中应力集中的影响,可以看到应力较大值分布在几个受力部件危险截面处。

图5 自密封结构主要受力情况Fig.5 Main stress conditions of self sealing structure

自密封结构中ab面、cd面、df面的受力和de截面的受力如图6 所示,在这几个受力面各取一个较均匀区域测量其应力,可知,ab面的受力在184.9 MPa左右,cd面的受力在160.1 MPa 左右,df面的受力在113.8 MPa 左右,de面的最大应力为181.3 MPa左右。

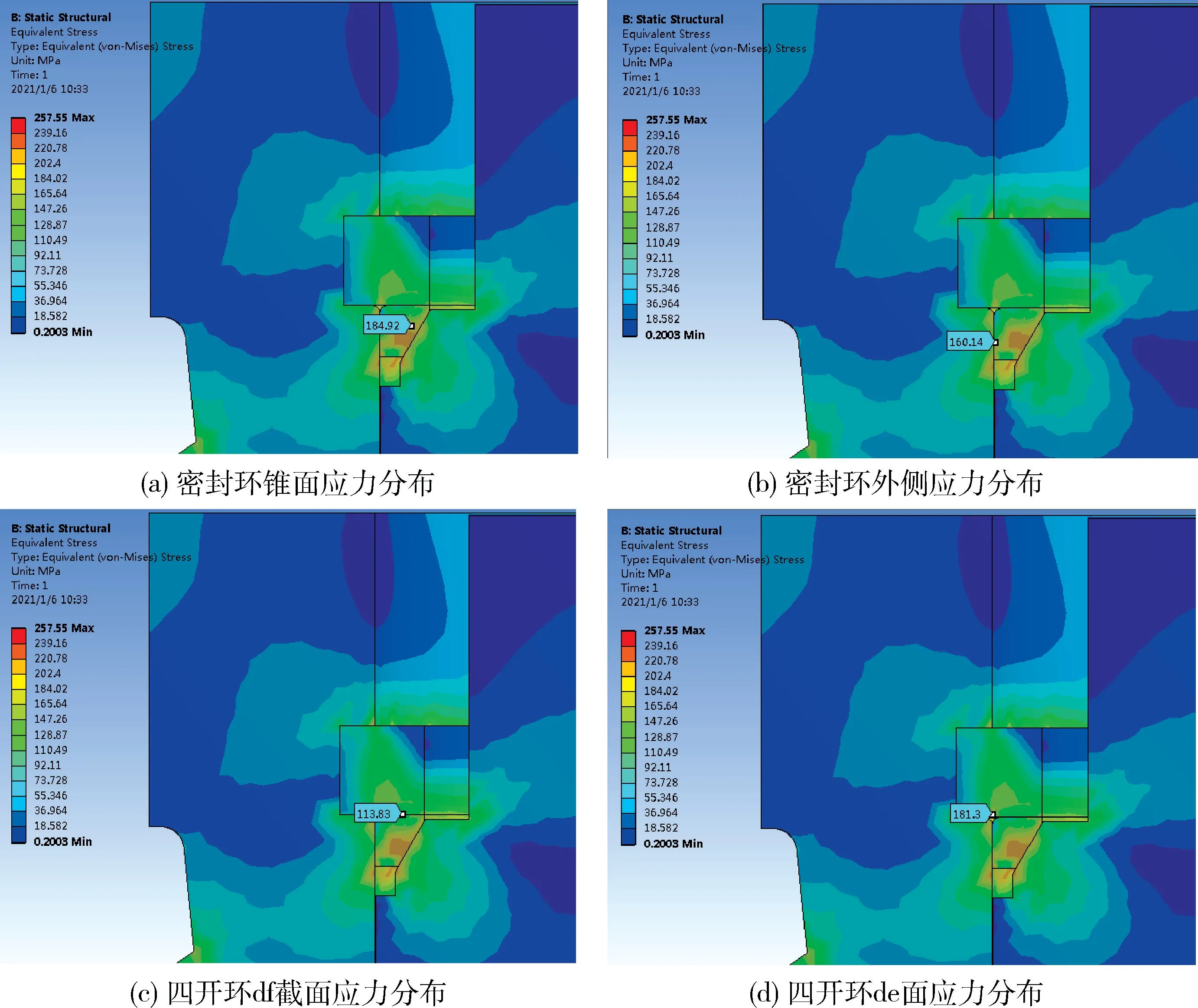
图6 危险截面受力分布Fig.6 Stress distribution of dangerous section

将表1 中数据代入式(1)—式(9),计算结果见表2。其中许用应力根据使用工况、环境等因素,会选择不同的安全系数,所以其值也会不同,本文取值如表2 所示。

表2 自密封结构受力计算值Table 2 Stress calculation value of self sealing structure

将理论计算值与数值模拟结果进行对比,如图7所示,两种方法计算结果相近,理论计算值比数值模拟结果偏大,是由于理论计算做了简化,忽略了摩擦等一些损耗。说明所推导计算公式还是较为符合实际,和分析相符,可以作为设计依据。

图7 理论值与数值结果对比Fig.7 Comparison of theoretical and numerical results

将计算结果σab、σcd与必需密封比压qMF1、qMF2比较,可知密封性能完全可以满足,符合设计需求。将计算结果与许用应力相比较,可知密封环ab面的挤压应力略大于许用,而四开环de截面的弯矩远大于许用弯矩,有发生破坏的隐患。因此,需对主要承力部件尺寸进行微调,增强其强度,以满足设计需求。

5 结论

(1)研究设计的中道自密封球阀结构,其中道有三道密封结构,密封性能优异,可以解决球阀在低温高压环境下中道螺栓预紧不足,易产生危险的隐患。同时,减少了球阀中道体积,极大的减轻了重量,节约了成本。

(2)推导出主要受力部件的计算公式,与数值模拟结果相对比,两种计算结果相近,计算方法可靠,可以为该种自密封结构设计提供理论依据。

(3)研究设计出的自密封球阀结构,提供一种新的大口径超高压球阀设计思路,推进国产化进程,为行业的发展提供理论参考。