高中数学教学中向量的整合分析

福建省莆田市仙游县华侨中学 陈建绸

高中数学和其他事物有着紧密的关联性，因此要在教学中体现出来，而想要达到这一效果，就要对数学教学方式进行整合，并和各章节保持密切的联系。向量是全新的内容，从学生的角度分析，学习新内容，除了能扩充知识储备以外，还可不断地提升学生的思维能力。教师要利用向量来对传统知识结构进行分析，并改变以往的认识，以此提高学生使用向量解决问题的能力。

一、在不等式证明中如何应用向量

一部分具有乘积、乘方之和的不等式，能够利用向量数量积的坐标表达式结构特点来进行不等式的证明。

通过上面的例题能够了解到，使用向量证明不等式非常方便，获得答案的重点为利用不等式的特点来构建两个符合要求的向量。

二、在解析几何中如何应用向量

在立体几何问题解答中，经常要充分使用向量，很多烦琐的几何题目均能够通过向量来转变模式，并利用机械性操作来完成。

数学课本当中所讲解的解题思路非常实用，是能够得到一些有关几何问题答案的最为合理的方式，也是基本的方式，而在掌握了平面向量内容之后，解答这种问题时会有更多收获。

例4：已知圆的方程为x2+y2=r2，求通过圆上一点M（x0，y0）的切线方程。

解：设N（x，y）是所求切线中的任意一点，

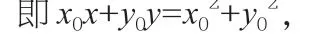
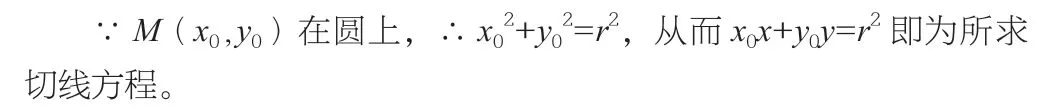
当然，例题不使用向量也能够获得答案，不过用向量法求解能够体现出特色，也更加方便。

平面向量在数学中属于一种运算对象，使用向量能够轻易解决很多数学难题，并使学生理解向量方法，从而提升学生分析、解决问题的水平，加强他们的创新能力。

三、向量在立体几何中的应用

因为向量融合了几何图形和代数，让其变成中学数学知识的交汇点，也变成了串联多类内容的媒介，所以在研究其他问题时得到了全面的应用，尤其是在解答立体几何的角度、垂直等问题的过程中得到了大量应用。

例6：在棱长相等的四面体ABCD中，E、F是棱AD、BC的中点，连接AF、CE，求异面直线AF和CE所成的角。

向量与高中数学的其他内容具有紧密的关联，所以在教学中，若合理地使用向量知识，更容易提升学生的解题水平。