Comparative Study on Structural Redundancy of Cable-Stayed and Extradosed Bridges Through Safety Assessment of Their Stay Cables

Khawaja Ali*, Hiroshi Katsuchi, Hitoshi Yamada

Department of Civil Engineering, Yokohama National University, Yokohama 240-8501, Japan

Keywords:Cable-stayed bridge Extradosed bridge Redundancy Stay cable Safety factor Reliability analysis

ABSTRACT This study provides new insights into the comparison of cable-stayed and extradosed bridges based on the safety assessment of their stay cables.These bridges are often regarded as identical structures owing to the use of inclined cables; however, the international standards for bridge design stipulate different safety factors for stay cables of both types of bridges.To address this misconception,a comparative study was carried out on the safety factors of stay cables under fatigue and ultimate limit states by considering the effects of various untoward and damaging factors,such as overloading,cable loss,and corrosion.The primary goal of this study is to describe the structural disparities between both types of bridges and evaluate their structural redundancies by employing deterministic and nondeterministic methods. To achieve this goal, three-dimensional finite-element models of both bridges were developed based on the current design guidelines for stay cables in Japan.After the balanced states of the bridge models were achieved, static analyses were performed for different safety factors of stay cables in a parametric manner. Finally, the first-order reliability method and Monte Carlo method were applied to determine the reliability index of stay cables.The analysis results show that cable-stayed and extradosed bridges exhibit different structural redundancies for different safety factors under the same loading conditions.Moreover, a significant increase in structural redundancy occurs with an incremental increase in the safety factors of stay cables.

1. Introduction

Structural engineers have always advocated spanning cablestayed bridges (CSBs) over river crossings and straits because of their structural efficiency and aesthetic appeal. The idea of CSBs emerged when suspension bridges were being developed; however,at the beginning of the 19th century,the failures of early CSBs caused this idea to be abandoned temporarily owing to the lack of technical knowledge in dealing with the difficulty of analyzing CSBs and the lack of suitable materials for stay cables. Stay cables were introduced again as supplementary components in the construction of suspension bridges at the end of the 19th century,such as for the Brooklyn Bridge, to increase the bridge stiffness against wind-induced vibration, which highlighted the paramount importance of using stay cables in long-span bridges. The first modern CSB was the Tempul Aqueduct built in the 1920s in Spain by Eduardo Torroja, a pioneer structural engineer [1]. Internationally,the development of CSBs began in the 1970s, but the rapid advancements in computer applications in 1990s proved to be a huge step forward. Bridge engineers started developing a better understanding of modern CSBs. Among other investigations,Lozano-Galant and Paya-Zaforteza [2] performed a detailed analysis of the influence of structural systems and removal of live loads on the behavior of the Tempul Aqueduct to describe the evolution of the design of modern CSBs.

In addition to the evolution of such bridges, the concept of extradosed bridges (EDBs), invented by Jacques Mathivat [3], has been widely recognized in the construction industry over the past few decades. The first modern EDB in the world was the Odawara Blueway Bridge designed by Kasuga et al. [4,5], a chief engineer in Sumitomo Mitsui Construction Co.,Ltd.,Tokyo,Japan,in 1994.Both the CSB and EDB seem to have identical structures because both types of bridges use stay cables to connect the deck with the towers. However, their structural behaviors are different because of their different height-to-span ratios. Many researchers [5-8] have performed analytical studies to compare the structural systems of CSBs and EDBs, and they defined the EDB as an intervenient solution and hybrid bridge structure between CSBs and prestressed concrete bridges (PCBs). In the case of CSBs, a major part of the dead and live loads is carried by the stay cables,whereas a stiff girder without any stay cable carries all dead and live loads in the case of a PCB. Intriguingly, an EDB possesses partial roots from CSBs and PCBs, in which the dead loads are distributed between the stay cables and the girder, and a major part of the live load is carried by the stiff girder. Thus, the redundancy of CSBs and EDBs is largely dependent on the safety of stay cables, which is usually ensured by providing a suitable safety factor.By definition,redundancy is the ability of a structure to redistribute the loads through different paths following the failure of any single component.

Many international standards for bridge design stipulate different safety factors for the design of stay cables of CSBs.For example,the Japanese specifications for highway bridges[9]suggest a safety factor of 2.5, resulting in a stay stress of 0.4σUTS(where σUTSdenotes the ultimate tensile strength) compared with the safety factor of 2.22 used in the United States and Europe [10]. This means that Japanese regulations stipulate a higher safety factor value for the stay cables of CSBs. To investigate the suitability of the current safety factor of stay cables in Japan, Ali et al. [11] performed a parametric study on the safety factor of a CSB under the fatigue limit state(FLS)and ultimate limit state(ULS)by considering the effects of various loading conditions, and the results showed a promising agreement in the establishment of the current safety factor of stay cables of CSBs in Japan. However, most of the international standards for bridge design have not suggested a suitable safety factor for the stay cables of EDBs. In 1994, Shirono et al. [4] adopted a reduced safety factor of 1.67 against σUTSfor the Odawara Blueway Bridge based on a comparative study of fatigue demand for stay cables of CSBs and EDBs [5,12]. This resulted in a higher allowable stress of 0.6σUTSin cables and more-efficient use of cable materials [13].

In establishing a safety factor of a cable, the following factors are usually considered: ① ratio of live-to-dead load stress,②occurrence frequency of live load stress, ③effect of the secondary stress, ④stress nonuniformity, ⑤balance with the safety factors of other components, and ⑥damage occurrence resulting from fatigue and corrosion. Recently, the Japanese specifications for the design of stay cables have been revised so that the safety factors are stipulated based on the live-to-dead load ratio [14].According to the new guidelines,the design of stay cables is carried out based on the axial stress in stay cables instead of by defining whether stay cables belong to CSBs or EDBs, and stress ratios of 1.0 and 0.1 yield safety factors of 2.5 and 1.67 for stay cables of CSBs and EDBs,respectively.Thus,it is possible to design each stay cable separately and to set the allowable stress limits for each stay cable individually without declaring the bridge type [13]. Table 1shows the allowable stress limits (and safety factors) stipulated in different standards for the design of stay cables of CSBs and EDBs[14-19].

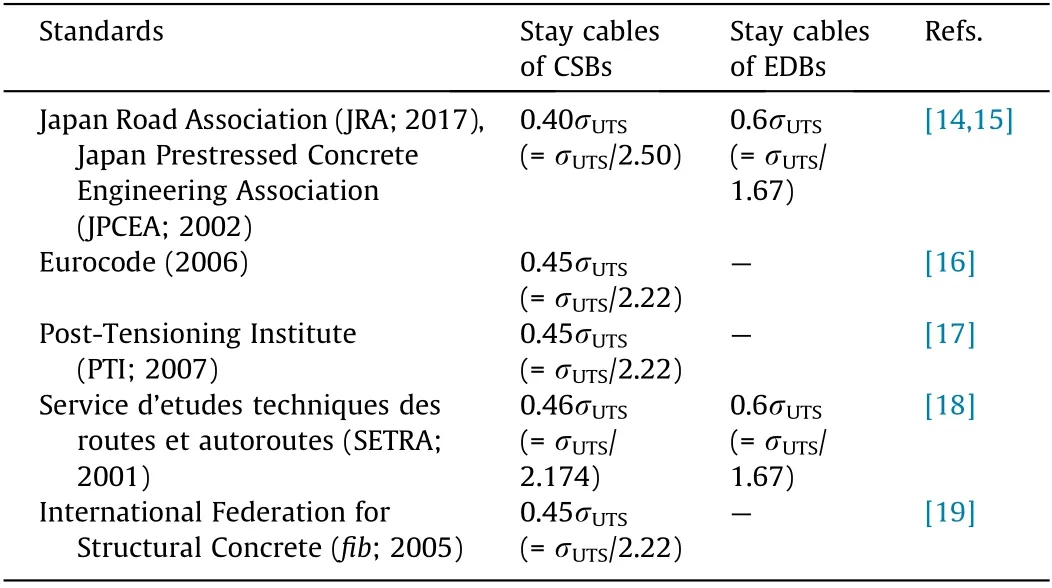
Table 1 Allowable stress limits recommended by international standards for stay cables.

However,there is still a debate concerning the structural redundancies of CSBs and EDBs,especially considering the current safety factors of their stay cables.To what extent the redundant CSBs and EDBs can remain structurally sound under various extreme loading conditions is still unclear. This is because the stay cables of a CSB act as elastic supports for lifting the bridge deck,whereas the stay cables of an EDB are considered as external tendons arranged outside the prestressed concrete girder [12]. Therefore, it is worth comparing various aspects of CSBs and EDBs, including the effects of overloading, fatigue, and corrosion on the demand-to-capacity ratios (DCRs) of stay cables for different safety factors, by using the limit state design method in a parametric manner.

In the current design practice, the redundancy of cablesupported structures is determined through an experience-based evaluation method by establishing an acceptable safety margin between strength and loading effects[20].However,with an ordinary structural analysis using a deterministic method,it is difficult to clearly understand the behavior of a bridge structure and to precisely examine its safety level in the presence of uncertainties included in the design variables. Moreover, questions often raised in practice are about the current safety factor of stay cables and to what extent the safety factors are adequate in terms of safety and economy. Therefore, it seems reasonable to assess reliability considering all kinds of uncertainties i.e., environmental conditions, variations in live loads, and intrinsic manufacturing uncertainties, such as axial stiffness, self-weight, yield, and ultimate strengths of cables [21]. Many researchers have developed frameworks for performing reliability-based studies on structures to evaluate their current situation and economic life. Czarnecki and Nowak [22] developed a time-variant reliability-based model for the evaluation of steel highway bridges subjected to uniform corrosion by idealizing it as a uniform loss of the surface material of the structural member. Maljaars and Vrouwenvelder [23] used the Monte Carlo (MC) simulation method to calculate the failure probability and reliability index of cables containing fractured wires for the fatigue assessment of an existing bridge. Lu et al.[24] presented a framework for system reliability evaluation of in-service CSBs subjected to cable degradation by considering the effects of fatigue damage and corrosion on cables in a parallelseries system. Reliability analysis has become an indispensable approach for evaluating the performance and remaining life of a bridge.

A comparative study was conducted on a CSB and an EDB to investigate and compare their structural redundancies through the safety assessment of stay cables in a parametric manner under various untoward and damaging conditions. First, threedimensional (3D) finite-element (FE) models of both bridges were developed based on the safety factors of stay cables stipulated in the design guidelines. Thereafter, a multiconstraint optimization technique of unknown load factors was applied to compute the optimal cable forces.Subsequently,static analyses were performed under FLS and ULS to evaluate the structural redundancy of CSBs and EDBs deterministically in terms of the DCRs of stay cables for different safety factors. The effects of overloading, cable loss,and corrosion, as well as their coupling effects, on the safety level of stay cables were also investigated. Finally, the first-order reliability method (FORM) and MC method were employed to assess the structural redundancy in terms of the reliability index of stay cables.The analysis results showed that CSBs and EDBs exhibit different structural redundancies for different safety factors of stay cables under the same loading conditions. A significant increase in structural redundancy was also observed with an incremental increase in the safety factor of stay cables.

2. Finite-element modeling

2.1. Cable-stayed bridge

A 3D FE model of a double-plane CSB with a main span of 460 m and two side spans of 220 m was developed using the MIDAS Civil(MIDAS Information Technology Co., Ltd., Korea) bridge modeling software [25]. The structural configuration of the bridge model is shown in Fig. 1. The longitudinal slope of the bridge floor was designed to be 2%. To facilitate the analysis, the cross section of the girder was simplified as a thin-walled box section with the equivalence of area and inertia of moment. The total width and depth of the steel box girder were 21.75 and 3.5 m, respectively,with four traffic lanes. In addition, two 1.75 m wide pedestrian lanes were considered, as shown in Fig. 2. The number of stay cables of a CSB-Cs was 144, and they were placed at a constant cable spacing of 12 m on the deck level. The ultimate tensile strength of CSB-Cs made of parallel strands was assumed to be 1770 MPa with reference to Japan Industrial Standards Committee(JIS) G3525 [26], and they were arranged in a modified-fan style.These cables acted as an elastic support for the deck; hence, multiple cables increased the number of elastic supports, leading to moderate longitudinal bending in the deck.Moreover,the multiple cables reduced the forces in the stay cables. An H-shaped configuration of the tower was selected with a height of 140 m (pylon:115 m; pier: 25 m). The pylon height was chosen as one quarter of the center span length such that the angles subtended by CSBC1 and CSB-C36 should be greater than 25° with respect to the bridge longitudinal axis to prevent the stay cables from being ineffective. In addition, it was assumed that the CSB-Cs were selfanchored to the bridge deck. Regarding the bridge connections and boundary conditions,the bridge girder was supported by roller supports on both sides,enabling the longitudinal movement of the bridge model, whereas the pier foundation was assumed to be fixed. Furthermore, elastomeric rubber bearings were simulated as elastic links to connect the bridge girder with the lower transverse beams. The girder and the towers were modeled as elastic beam elements, whereas stay cables were modeled as truss elements (tension only). A fishbone modeling technique was implemented to connect the stay cables with the deck spine through rigid links.

2.2. Extradosed bridge

Similar to the CSB,a 3D FE model of a 408 m long double-plane EDB was developed by using MIDAS Civil [25]. The center span length was 208 m, and the two side spans were each 100 m long.The structural configuration is shown in Fig. 3. The total width and depth of the prestressed concrete box girder were 21.75 and 4.5 m, respectively, with four traffic lanes, as shown in Fig. 2. The EDB model was also cambered linearly by a longitudinal slope of 2%. The bridge girder was supported by the piers and by a system of stay cables of an extradosed bridge (EDB-Cs). The anchorage points of the EDB-Cs at the deck level are located at intervals of 5 and 6 m on the side and center spans, respectively. In addition,the ultimate tensile strength of EDB-Cs (made up of parallel wire strands) was assumed to be 2000 MPa with reference to JIS G3525 [26]. The height of the concrete tower was 40 m (pylon:22 m; pier: 18 m) because the pylon height was chosen as one ninth to one tenth of the center span length in the case of the EDB.The concrete girder and towers were modeled as elastic beam elements,whereas the stay cables were modeled as truss elements.A fixed and monolithic connection was assumed between the towers and girder because the stress range resulting from the live load in the EDB-Cs was influenced by the girder stiffness and fixity of the support on the piers. When a girder is stiff, the stress range in the cables caused by the live load is small compared with the dead loads.To reduce the magnitude of this stress range,the girder of the EDB was fixed at the piers.The fixity of the girder,both at the side span supports and on the main piers,has a significant effect on the bending moment in a girder and on the stress range in cables resulting from the live load. This is because the live load on an EDB is shared between the stay cables and the girder. Fixing the girder at the piers makes it possible for the bridge to resist a live load, causing a shift in the bending moment of the loaded span from positive to negative moment regions, where the moment is distributed into the piers. Moreover, fixing the girder decreases the displacements, especially in the spans adjacent to the applied load [8].

2.3. Design considerations for CSB and EDB

For the design of the CSB and EDB, dead and live loads were referred to the Japanese specifications for highway bridges [9].The material and sectional properties of the bridge components are shown in Tables 2 and 3,respectively.Tables 4 and 5 represent the design loads used for both bridges. Dead loads (including the self-weight of the girder), pavement load, and additional loads were applied uniformly on the entire span of the bridge models.L-type live loads were considered in the structural analysis, consisting of a concentrated live load (S1) of 10 kN·m-2acting over a length of 10 m and a uniformly distributed live load (S2) of 3 kN·m-2imposed over the entire length. Additionally, a pedestrian load of 3 kN·m-2was considered for the design of the girders.EDBs are usually constructed with a concrete box girder ranging from short to medium in span, whereas CSBs are preferably constructed with the steel box girder ranging from a medium to long in span; therefore, the CSB and EDB in this study were designed with different lengths, materials, and sectional properties. However,the loading conditions were assumed to be the same for both bridge models for comparison purposes.

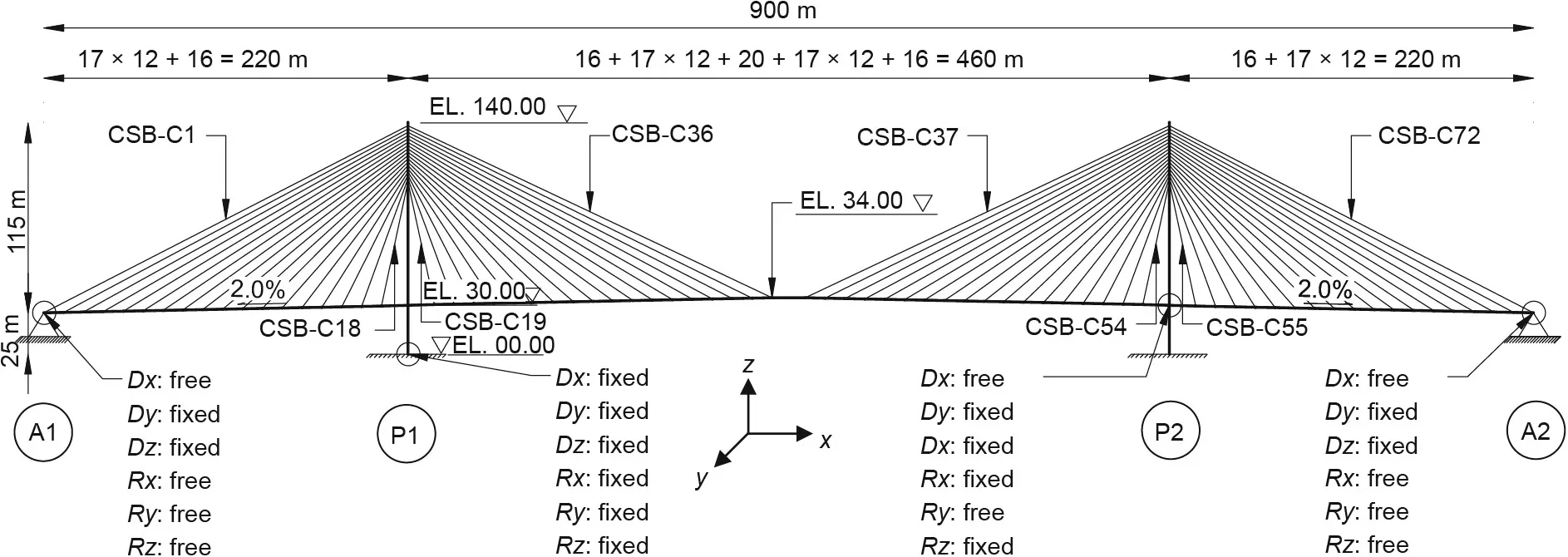
Fig.1. Configuration of CSB model.A1 and A2 refer to anchorages;P1 and P2 refer to main pylons;Dj and Rj(j=x,y,and z)denote the translational and rotational degrees of freedom, respectively; EL. denotes the elevation.

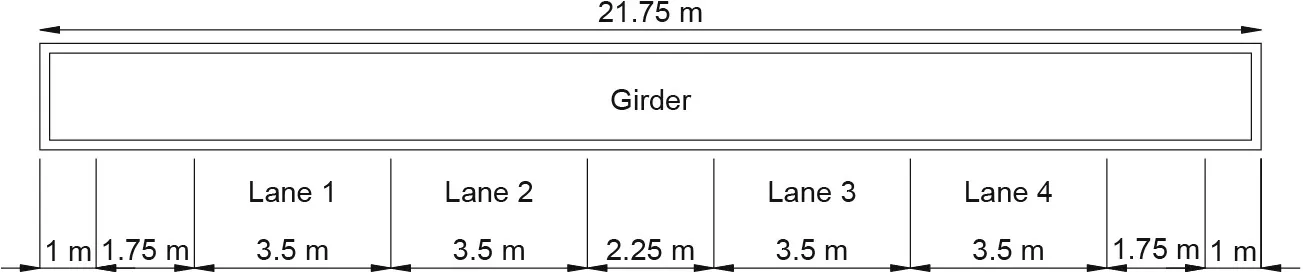
Fig. 2. Configuration of traffic lanes.

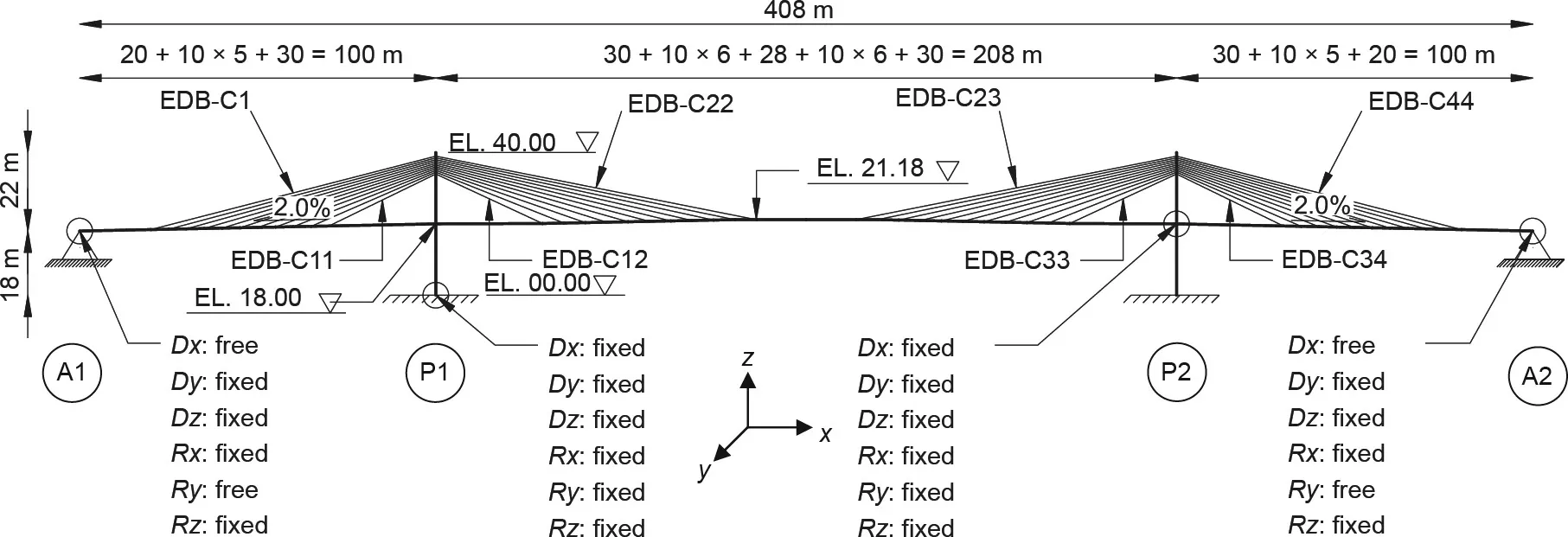
Fig. 3. Configuration of EDB model.

Table 2 Material properties of bridge components.

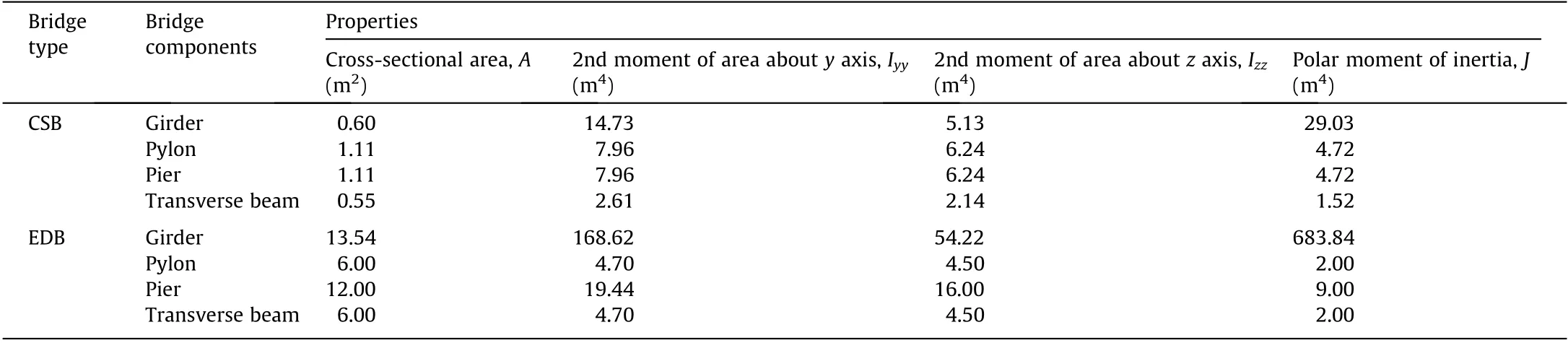
Table 3 Sectional properties of bridge components.

Table 4 Dead loads, pavement loads, and additional loads.

Table 5 Live loads.

2.3.1. Stay cables of cable-stayed bridge

In the case of the CSB, each stay cable was designed under the conditions that the live-to-dead load ratio is 0.45 and the allowable stress is 708 MPa. The multiconstraint optimization technique of unknown load factors was applied to tune the pretension cable forces (PS). This technique is efficient for distributing the moment uniformly along the bridge deck and minimizing the member stresses and deflections [27]. Many iterations were performed to achieve the equilibrium state of the CSB under its own selfweight. Subsequently, the corresponding cross-sectional areas of the CSB-Cs were calculated.In addition,CSB-Cs were designed such that the axial stresses were approximately 50%-60% of the allowable stress under the dead load and were less than the allowable stress under dead and live loads [11].

2.3.2. Stay cables of extradosed bridge

The challenge of designing an EDB with a stiff girder lies in proportioning the girder,cables,and substructure to control the stress range in the cables resulting from the live load and to take advantage of the higher allowable stress of low fatigue cables. The EDBCs were designed under the conditions that the live-to-dead load ratio is 0.11 and the allowable stress is 1198 MPa. For calculating the PS of EDB-Cs, the continuous beam method was applied. An iterative procedure was adopted to determine the equilibrium state of the EDB under the action of a dead load, and the crosssectional areas of EDB-Cs were optimized accordingly. An internal prestress force(Pi)was also applied to the prestressed concrete girder in the case of an EDB to ensure that the girder did not crack,minimize the deflection,and resist the bending moments resulting from the long-term effects and live loads [8].

2.3.3. Nonlinearity effects

The axial stiffness of stay cables in a CSB is affected by the cable sag, which is greatly influenced by the tension force in the cable.When the tension force increases, the sag effect decreases, and the axial stiffness increases accordingly. A convenient method to account for this variation in axial stiffness is to consider an equivalent truss element with an equivalent modulus of elasticity.Studies have shown that geometric nonlinearity is essential for the nonlinear analysis of CSBs subjected to cable breakage [28,29]. In this study,the geometric nonlinearity effects were considered in the static analyses of both bridges in terms of tension stiffening effects using a reduced or equivalent modulus of elasticity. This approach was first proposed by Ernst [30] to consider the nonlinear behavior of cables, such as:

where Eeqis the tangential value of the equivalent modulus of elasticity, E is the modulus of elasticity, A is the cross-sectional area of the stay cable, w is the cable weight per unit length, L is the horizontal projected length, and T is the tensile force in the stay cable.For EDBs,the horizontal projected length of stay cables is short,and the tension force T in stay cables under dead load is extremely large; therefore, the modulus of elasticity of EDB-Cs is not significantly affected by sag effects.

2.4. Static analysis

Several live load patterns were generated and applied to both bridge models, as illustrated in Fig. 4. The aim was to envisage the effects of pattern loads on the axial stresses of stay cables and to determine the most distressing pattern that causes the maximum axial stress in stay cables. The following load combinations were used in the static analysis of the CSB and EDB.

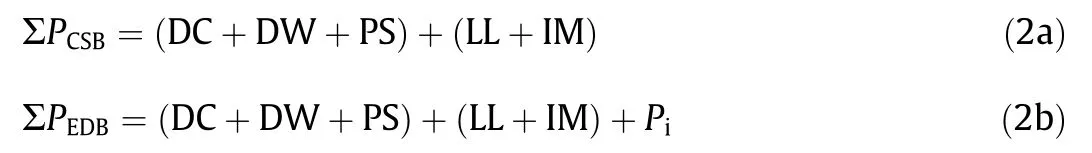
where ΣP is the sum of the unfactored axial load, DC is the dead load of components and attachment, DW is the dead load of wearing surface and utility, LL is the live load, IM is the dynamic load allowance, and Piis the internal prestress force. The static analysis results indicate that the effects of pattern load on the axial stress of CSB-Cs are more significant than on EDB-Cs,as shown in Figs.5 and 6,respectively.In the case of the CSB,CSB-C1 shows the maximum and minimum axial stresses under cases 2 and 3 of pattern loads,respectively, whereas cases 2 and 7 cause significant axial stress in stay cables CSB-C25-CSB-C27. A large variation is also observed in axial stress, depending on the locations of the stay cables and pattern loads in the CSB owing to the high flexibility and low damping.Moreover,the live-to-dead load stress ratio(1.25σL/1.05σDP) is estimated to be unity for CSB-C1. However, in the case of the EDB,cases 2 and 7 of the pattern loads yield nearly the same axial stress in the EDB-Cs because the live load, located in the center span,increases the anchorage forces within the back stays,while the live load within the side span decreases the anchorage forces. The maximum live-to-dead load stress ratio is 0.08 for EDB-C12. To simplify this problem, only case 2 of pattern loads was selected in this study to investigate the structural redundancy of both bridges.

3. Assessment of safety factor of stay cables

3.1. Fatigue limit state

For the fatigue assessment of stay cables, moving load analysis was performed under the fatigue design load (T-load: 200 kN)applied to the FE models of the CSB and EDB.Thereafter,the influence line diagrams (ILDs) of the internal axial force in the stay cables were drawn using the Breslau-Muller principle, and the maximum and minimum design variables were estimated for each stay cable.Subsequently,the cable reversal stress and design stress range (Δσd) values were computed by applying cyclic loading of constant amplitude and fully reversed nature according to the guidelines of fatigue design recommendations for steel structures[31]. Finally, the high cycle fatigue of a stay cable, based on the equivalent stress range theory, was assessed by satisfying the following relationship.

where γ is the safety factor equal to 1.0 based on the redundancy and importance of the structure,Δσdis the design stress range(also known as the ‘‘maximum stress range”), and ΔσRis the allowable stress range, which is simply calculated by multiplying the basic allowable stress range(ΔσCE)with a correction factor(CR)for mean stress, such as:

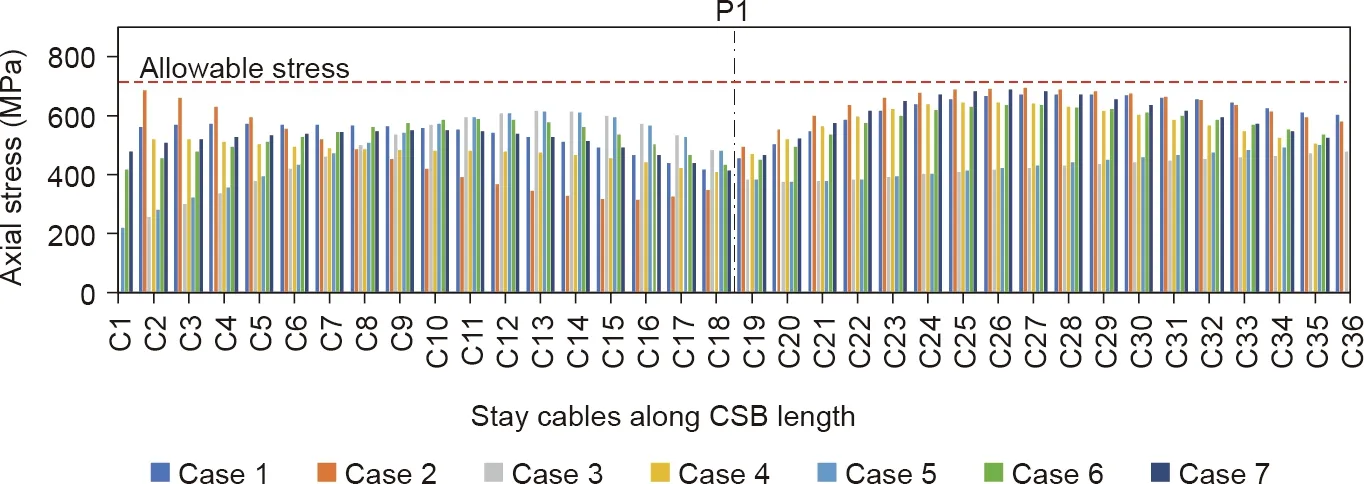
Fig. 5. Axial stresses in CSB-Cs under pattern loads.

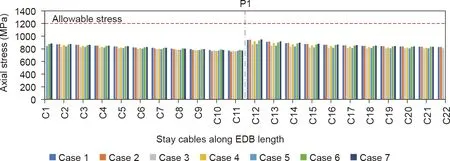
Fig. 6. Axial stresses in EDB-Cs under pattern loads.

In Eq. (4), the cutoff limit or basic allowable stress range is referred to the recommendations for stay cable design, testing,and installation[17],i.e.,159 and 140 MPa for the stay cables of the CSB and EDB, respectively, in accordance with two million load cycles. The correction factor for mean stress is computed on the basis of the stress ratio (R), which is the ratio of the minimum to maximum stress experienced during a load cycle, as follows:

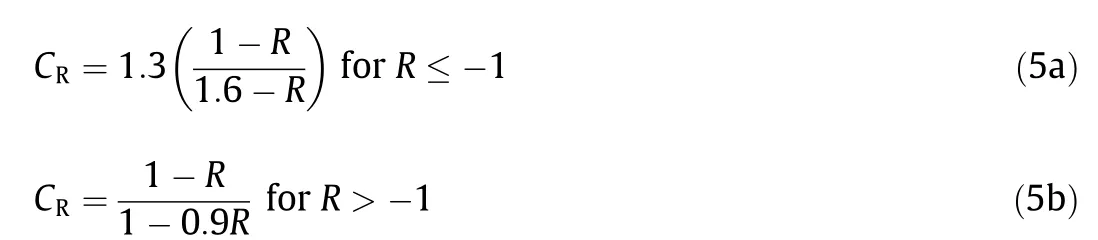
The ILDs of axial forces in CSB-C1 and EDB-C1 are shown in Fig.7,which indicates that CSB-C1 yields a larger area of ILD compared with EDB-C1 under the same fatigue loading condition.This shows that the effects of fatigue loads are significant and very small on CSB-C1 and EDB-C1, respectively. However, this trend may vary for other sets of CSB-Cs and EDB-Cs. Additionally, the effects of fatigue loads on each stay cable of the CSB and EDB are illustrated in Figs. 8 and 9, respectively. In case of the CSB, CSBC17 shows the maximum DCR, and a significant variation is observed in the DCRs of stay cables along the bridge length owing to the variable axial stresses. Moreover, the DCRs of CSB-Cs were less than unity at a current safety factor of 2.5, and these values increased linearly when the safety factor was reduced from 2.5 to 2.0. For instance, CSB-C17 exhibited DCRs of 0.81 and 1.01 at safety factors of 2.5 and 2.0,respectively.The minimum safety factor needed to achieve a DCR of less than unity is 2.1. This means that the safety factors in the range of 2.1 to 2.5 are reasonably safe for CSB-Cs under the FLS to achieve the desired structural redundancy. However, the EDB-Cs possess low fatigue characteristics and show DCRs less than unity, even at a safety factor of 1.6, as illustrated in Fig. 9. This can be attributed to the high rigidity of the EDB.Moreover,all stay cables depict almost the same magnitude of DCRs irrespective of their locations with respect to tower-deck connection. These results ensure the adequacy of the current safety factor of 1.67 for EDB,which provides enough structural redundancy to maintain stability under the effect of fatigue loads.

3.2. Ultimate limit state

The ULS check for stay cables must be performed after the preliminary design and after having been checked under the FLS.Therefore, Eq. (6) must be verified [31].

where γiis the structural importance factor equal to 1.0, Nrdis the design resistance of the stay cable,and Nuis the ultimate axial load.The design resistance of stay cables is calculated by multiplying the material yield strength with the cross-sectional area, whereas the ultimate axial loads on the CSB-Cs and EDB-Cs are calculated by using the load combinations mentioned in Eqs. (7a) and (7b) in accordance with American Association of State Highway and Transportation Officials (AASHTO) [32]. A load factor of k is adopted for live loads, simulating the effects of bridge overloading. Furthermore, PS and Piare not factored with the same coefficient of dead load in the case of the EDB, which is more reasonable for bridges with a rigid deck [8].

Fig. 7. ILDs of axial forces in CSB-C1 and EDB-C1.

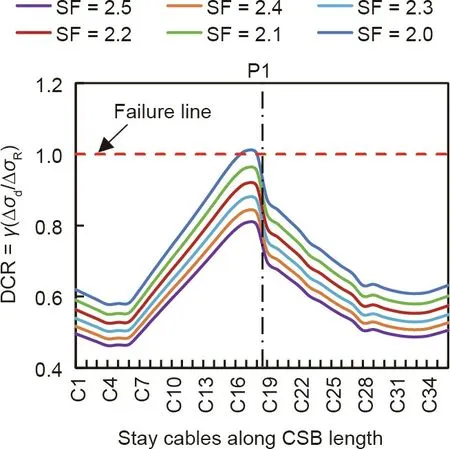
Fig. 8. Effects of fatigue on DCRs of CSB-Cs. SF: safety factor.

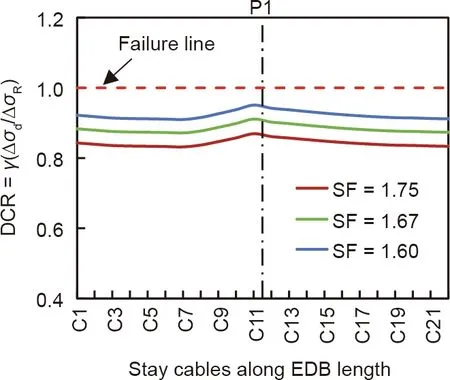
Fig. 9. Effects of fatigue on DCRs of EDB-Cs.

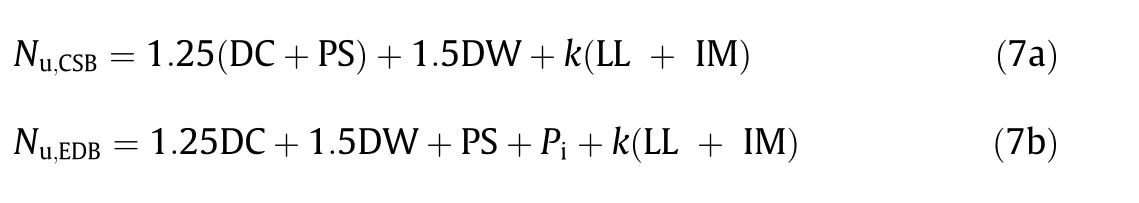
3.2.1. Effect of overloading

To study the effects of ultimate loads on a bridge structure,AASHTO[32]stipulates a live load factor(k)of 1.75 in the strength I load combination of the limit state,whereas the Japan Prestressed Concrete Institute[33]recommends a k of 2.5 for the calculation of ultimate collapse loads. Thus, in this study, k was selected in the range of 1.75 to 2.5, i.e., k1= 1.75, k2= 1.9, k3= 2.0, k4= 2.2, and k5= 2.5, for the examination of the structural redundancy of both bridges against ultimate loads. Fig. 10(a) shows that the DCRs of CSB-Cs are less than unity under k1at a safety factor of 2.5,whereas the DCR of CSB-C1 approaches unity at less than k5,which means that the current safety factor yields sufficient redundancy for all CSB-Cs under k1-k4. Similarly, the DCRs of CSB-Cs are less than unity with a small margin at a safety factor of 2.2 under k1;however, the DCR of CSB-C1 approaches unity under k3, which indicates that a safety factor of 2.2 is marginally safe with low redundancy for all CSB-Cs under k1and k2, as shown in Fig. 10(d).In the case of the EDB, the DCRs of EDB-Cs are less than unity at a current safety factor of 1.67 under k1, whereas the stay cables EDB-C12-EDB-C16 exceed the ultimate limit under k2-k5, as shown in Fig. 11(a). This indicates that the current safety factor is safe under a normal live load factor of k1; however, this safety factor should be increased in the case of overloading to avoid any cable failure.

3.2.2. Effect of cable loss

From the design viewpoint of long-span cable-supported bridges,the Post-Tensioning Institute(PTI)recommendations suggest two load application methods to quantify the dynamic effects of cable loss: One is the pseudodynamic method, in which the equivalent static analysis is performed with a pair of impact pseudodynamic forces,resulting from 2.0 times the static forces applied at the top and bottom anchorage locations of the ruptured cable,and the other is nonlinear dynamic analysis,in which the dynamic cable forces caused by cable breakage are applied [17]. Many researchers have implemented both methods to investigate the effect of a single cable loss on the local and global stability and safety of a CSB to develop a better understanding of how to make structures more redundant or collapse resistant[28,34-36].Mozos and Aparicio[37,38]conducted a parametric study on the dynamic response of CSBs subjected to the sudden failure of a cable. Ten CSBs with various layouts of stay and cable patterns were studied by conducting both dynamic and simplified static analyses. In addition,what happens to adjacent cables when a cable or multiple cables are lost because of any unexpected event, such as a fire accident or vehicle collision, has been the focus of discussion among bridge engineers[39].The breakage of a cable creates a sudden force on the anchorage points with which the cable is attached.This impact force is basically the cable force multiplied by a cable loss dynamic impact factor and is applied to both anchorage points in the opposite direction to the cable force, as stipulated in PTI guidelines. This factor depends on the location of the ruptured cable and the type of state variable being examined. In this study,a pseudodynamic method was adopted to investigate the influence of a single- or multiple-cable loss on the DCRs of stay cables of CSBs and EDBs. For this purpose, the longest stay cables, whose breakage can induce a significant axial stress in the adjacent cables,were selected in both bridges. The demonstration of cable loss impact force application is illustrated in Figs. 12 and 13 for a CSB and an EDB, respectively.

Fig. 10. Effects of overloading on DCRs of CSB-Cs. (a) Safety factor of 2.5; (b) safety factor of 2.4; (c) safety factor of 2.3; (d) safety factor of 2.2.

Fig. 11. Effects of overloading on DCRs of EDB-Cs. (a) Safety factor of 1.67; (b) safety factor of 1.75.

Fig. 12. Demonstration of cable loss impact force of CSB-C1 in CSB model.

Fig. 13. Demonstration of cable loss impact force of EDB-C1 in EDB model.

Static analyses were performed for different cable loss configurations of both bridges.Fig.14 compares the DCRs of CSB-Cs with and without the sudden loss of single-and multiple-stay cables for different safety factors. Fig.14(a)shows that the maximum DCR(0.88) of CSB-C1 is less than unity in the case of the loss of two cables (CSBC35 and CSB-C36) for the current safety factor. Similarly, the loss of a single cable (CSB-C36) on the main span side gives rise to a DCR of 0.86, less than unity, for CSB-C1 on the left-span side. As a corollary, a single-cable-loss event does not affect the safety of the CSB as much as a multiple-cable-loss event does. The loss of multiple cables on the main span side causes a high stress distribution in the back stays and vice versa, and the stress of any stay cable may exceed the allowable limit, causing the failure of more stay cables.This multiple-cable-loss event can also trigger a zipper-type collapse,also known as the ‘‘progressive collapse,” of the entire CSB. Fig. 14 also shows that,with the decrease in the safety factor of CSB-C1 from 2.5 to 2.2,the DCR increased linearly and reached the ultimate limit in the case of the loss of two cables(CSB-C35 and CSB-C36)at a safety factor of 2.2.This means that the safety factors of 2.5 and 2.3 are reasonably and marginally safe, respectively, for CSB-C1 to meet the requirements of the ULS.Fig.15(a)shows that the loss of two cables(EDB-C1 and CSB-C2)on the left-span side of the EDB yields a DCR of 1.04, greater than unity, showing a failure condition. This demonstrates that a safety factor of 1.67 yields sufficient redundancy only in the case of an intact state of the bridge; however, it should be increased in the case of an extreme damaging condition to enhance the redundancy of the EDB under the ULS. The results of the effects of cable loss at a safety factor of 1.75 are shown for the EDB in Fig. 15(b).

3.2.3. Effect of corrosion

The assessment of the safety of stay cables must also be quantified considering the effects of corrosion on the remaining strength of bridge cables in addition to their fatigue and ultimate capacities for lifetime safety evaluation of in-service CSBs.The loss of material decreases the geometric parameters, such as the moment of inertia and radius of gyration, resulting in a smaller net cross section that may increase the stress level for any given load or increase the stress range for a cycling loading, thus affecting fatigue resistance. The effects of corrosion, in addition to fatigue and overloading, on the safety of structures have been widely discussed in literature. Deng et al. [40] presented a simple uniform corrosion fatigue design method for bridge components by considering the coupled corrosion-overloading effects.It covers the individual effects caused by pure overloading, pure corrosion,and the corrosion-overloading interaction. Jiang et al. [41] proposed a general framework to estimate the corrosion fatigue life of stay cables under the combined action of random traffic and wind and showed that the coupled effects of corrosion and fatigue greatly reduce the lifetime of cable wires. This affects the overall bridge service life under certain corrosion rates.

In this study, a simple corrosion model was adopted by introducing a uniform corrosion of 10% throughout the cable length as a change in the cable area in reference to previous research[22,40,42,43]. The effective modulus of elasticity (Eeff) of the corroded cable was determined to be Eeff= (¯A/A）E, where ¯A denotes the cross-sectional area of corroded cable defined as the difference between the gross cross-sectional area (A) and impaired area (A*)of the cable resulting from corrosion, i.e., ¯A=A-A*. The effect of 10% corrosion and the coupled effects of 10% corrosion and cable loss on the DCRs of CSB-C1 and EDB-C1 were examined, and the results are presented in Fig. 16, focusing on the following two scenarios.

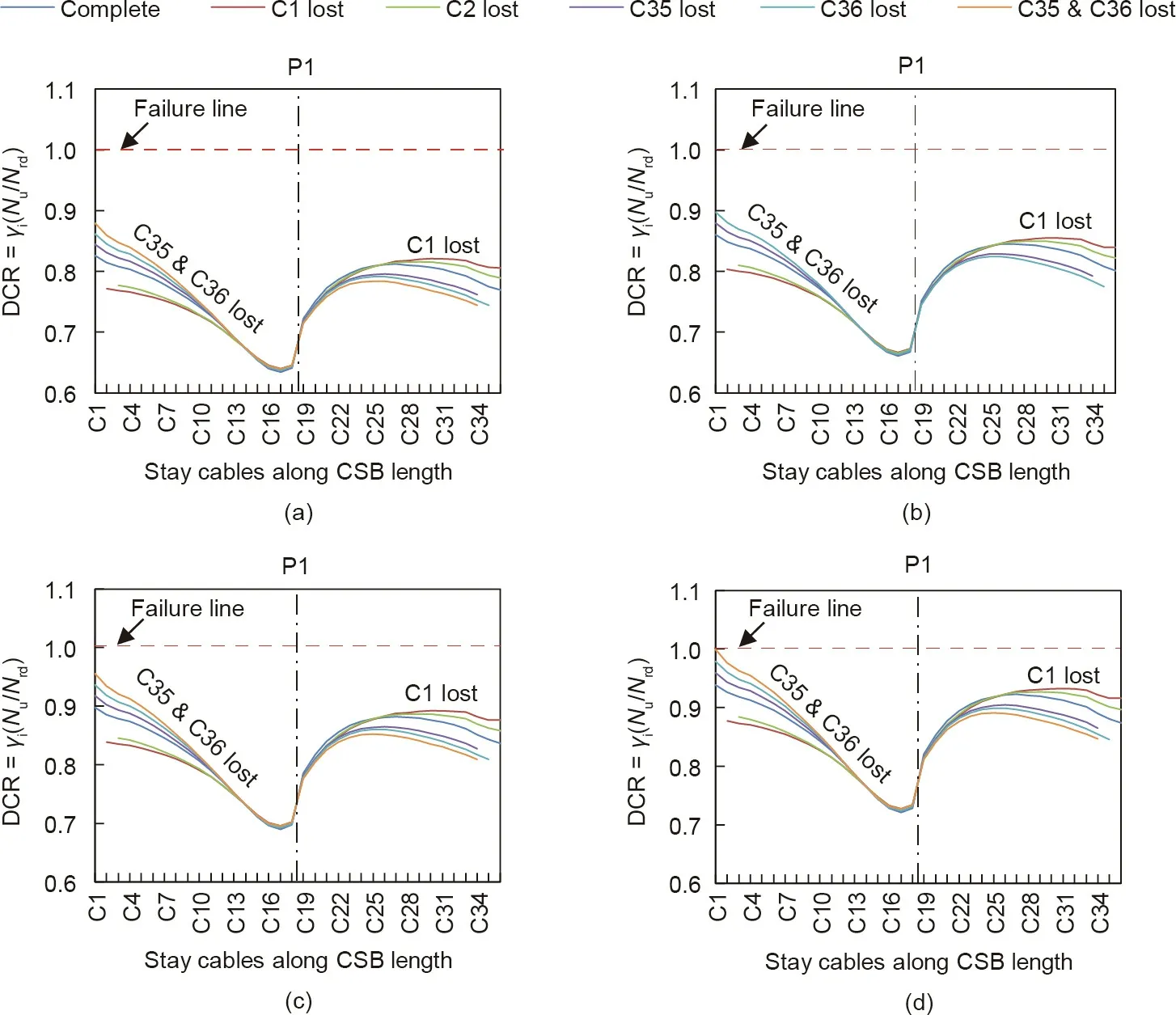
Fig. 14. Effects of cable loss on DCRs of CSB-Cs. (a) Safety factor of 2.5; (b) safety factor of 2.4; (c) safety factor of 2.3; (d) safety factor of 2.2.

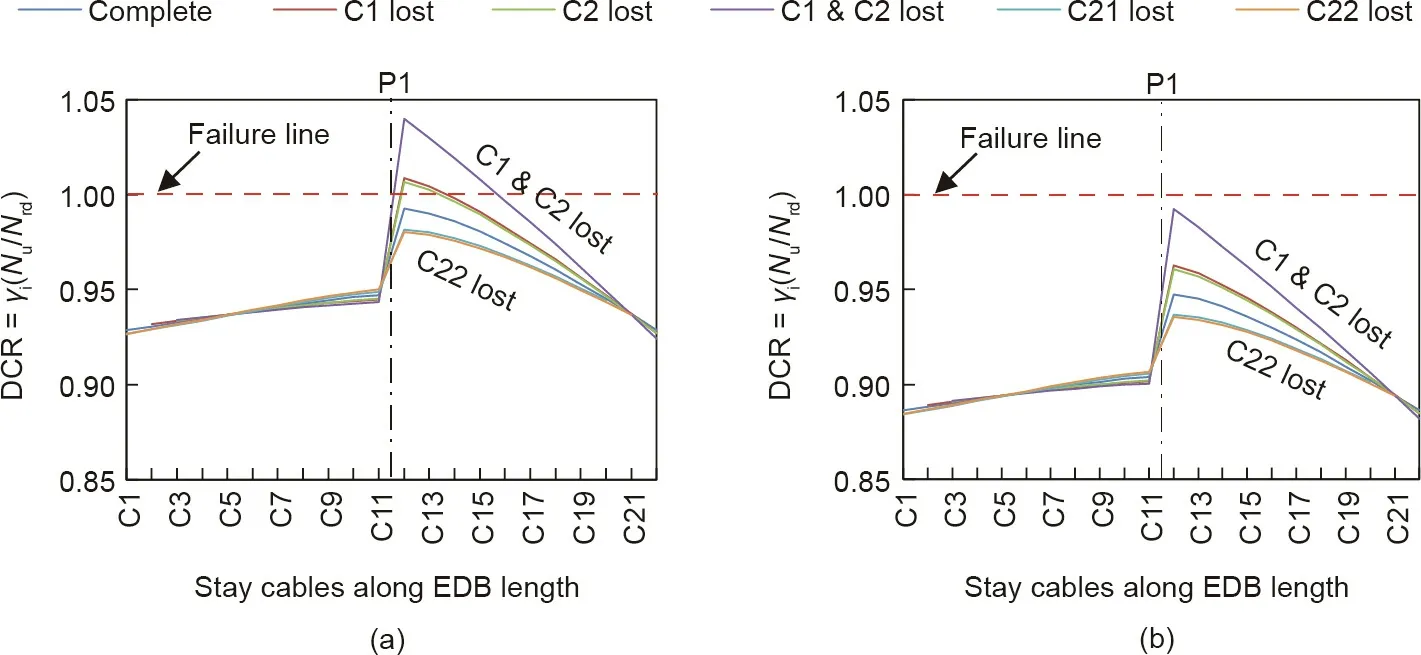
Fig. 15. Effects of cable loss on DCRs of EDB-Cs. (a) Safety factor of 1.67; (b) safety factor of 1.75.

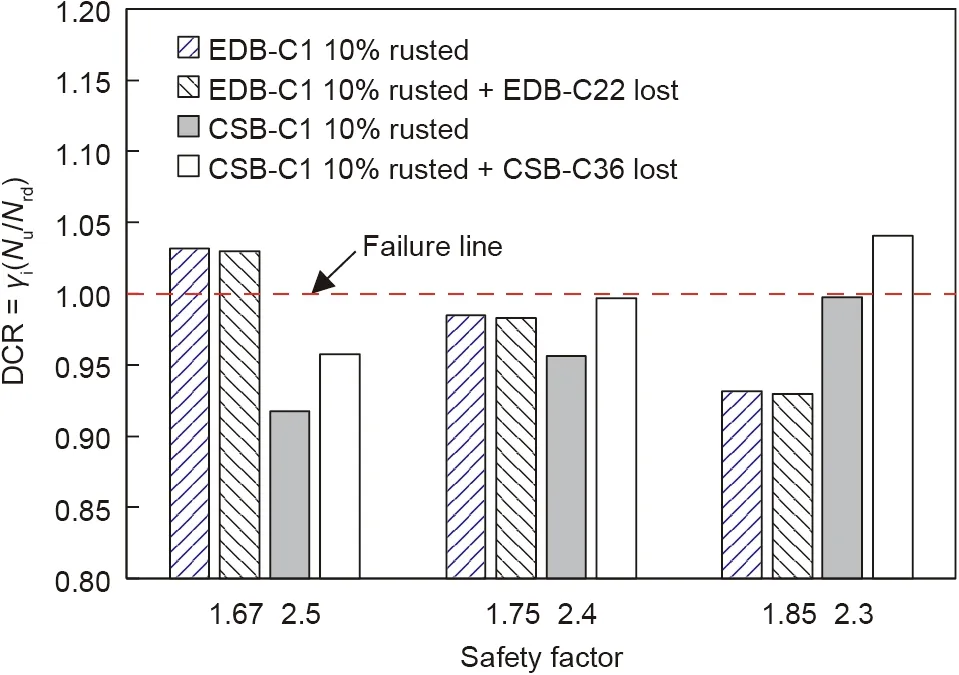
Fig.16. Coupled effects of corrosion and cable loss on DCRs of CSB-C1 and EDB-C1.

Scenario 1: When CSB-C1 and EDB-C1 are rusted by 10% uniform corrosion with no cable loss. In this scenario, the DCR of CSB-C1 is less than unity at a safety factor of 2.3, which indicates that a safety factor of 2.3 or more generates a reasonable redundancy. However, the DCR of EDB-C1 is greater than unity, even at a safety factor of 1.67, which indicates that a higher safety factor is required for EDB-Cs under extreme damaging conditions.

Scenario 2: When CSB-C1 and EDB-C1 are rusted by 10% uniform corrosion,and CSB-C36 and EDB-C22 are also lost.In this scenario,the DCR of CSB-C1 is estimated to be greater than unity at a safety factor of 2.3 and unity at 2.4.In fact,the DCR of CSB-C1 has a small safety margin of 2.5 under the coupled effects of corrosion and cable loss. This indicates the adequacy of the current safety factor for the safe design of a CSB with high redundancy.However,in the case of the EDB, the effects of a single cable loss in addition to corrosion are not as significant because of its high rigidity, as shown in Fig. 16.

3.3. Reliability analysis

In the investigation of the structural redundancy of a CSB and EDB based on a deterministic approach, it was assumed that all loads and mechanical and material factors involved in the structural behavior are known. In fact, these factors involve many uncertain quantities,such as material characteristics and load variations. Thus, a nondeterministic approach is inevitable for the examination of the structural redundancy of a CSB and EDB through a safety assessment of stay cables in a reliable manner.In this study, a load-resistance-based reliability model was adopted for the reliability analysis of stay cables under the FLS and ULS, in which load effects and resistances were assumed to be linear,uncorrelated,and normally distributed random variables.First, safety factors were used as an input to derive the working stress of the stay cables as a function of the fatigue and ultimate tensile strengths of the strands. Next, the fatigue and ultimate capacities were evaluated in terms of the working stress,and they were further used to investigate the probability distributions of the fatigue and ultimate capacities of the stay cables. However, the fatigue and ultimate demands for stay cables were derived based on the fatigue and ultimate design loads on the CSB and EDB,respectively.

A population of one million samples of loads and resistances was generated at random with the help of the MC sampling technique by using the programming language software MATLAB[44]. The required number of samples (N) to achieve a 95% confidence level and Pf= 1 × 10-4was estimated to be 50 000 with a minimum sample size of 170 under the condition that the standard error of the mean of sample means is within±5%.The distribution of sample means followed a normal distribution according to the central limit theorem,which states that the distribution of sample means approximates a normal distribution as the sample size becomes larger.The statistical parameters for the random variables of loads and resistances are quoted from previous research[45-47]and listed in Table 6.

To calculate the reliability index and failure probability (Pf) of the stay cables, the FORM and the MC method were applied. In the former, a linear limit state function was formulated with the help of two random variables (C: capacity; D: demand) under the FLS and ULS, and the safety margin (Z) was evaluated. Subsequently, the reliability index (β) was determined through a coupling equation that relates demand and capacity probabilistically using the mean (μ) and variance (σ) of C and D.

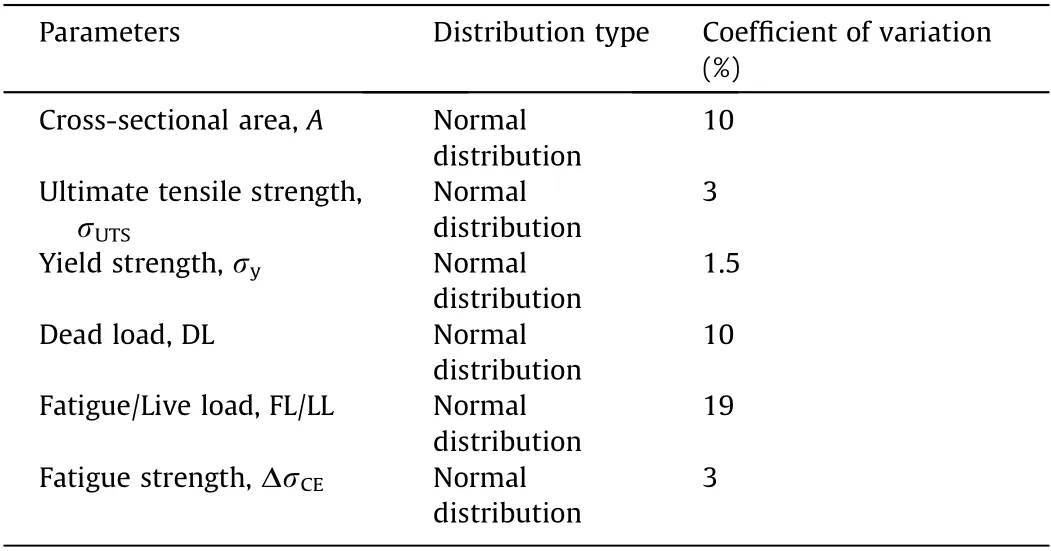
Table 6 Statistical properties of random variables for stay cables.

where g (·) is termed the limit state function, Nfis the number of samples that failed to satisfy the limit state, and N is the number of samples under consideration related to the desired accuracy for Pf. The reliability index of a structure is estimated from Pf, which indicates that the resistance exceeds the load effect.

where Φ-1(·) represents the inverse of the standard normal cumulative distribution function.

To verify the safety of structures,the United States Army Corps of Engineers recommended that the estimated reliability indices should minimally be ①the lower value of the target reliability index (βt，l) of 3 for above-average performance and/or ②equal to the upper value of the target reliability index (βt，u) of 4 for good performance[32,48].Table 7 shows the outcomes of the reliability analyses for CSB-C1 and CSB-C17 based on the FORM and the MC method under the ULS and FLS,respectively.The failure probability increased when the safety factor of the stay cables decreased from 2.5 to 2.1, and the reliability index decreased accordingly. For instance, the reliability indices of CSB-C1 and CSB-C17 estimated by the FORM in the vector forms are [25.04, 19.33, 13.56, 7.74,1.87]and[15.87,12.57,9.27,5.96,2.64]under ULS and FLS,respectively, at safety factors of[2.5,2.4,2.3,2.2,2.1].However,the reliability indices computed by using the MC method are mathematically infinite at a safety factor of 2.2 or more owing to the high safety margin. These results highlight the adequacy of a safety factor of 2.2,which yields a reliability index greater than βt，ufor CSB-C1 and CSB-C17.

To further investigate how redundant the entire CSB can be at a safety factor of 2.2, the reliability indices of all CSB-Cs along the bridge length were determined under the ULS and FLS, and the results are plotted in Fig.17(a).A significant variation in the reliability indices of CSB-Cs along the CSB occurred owing to the high flexibility.A safety factor of 2.2 or above was found to be necessary to achieve the desired structural redundancy under the FLS and ULS for the entire CSB stay system. Furthermore, Fig. 17(a) illustrates that the longer stay cables were not as sensitive to fatigue loads as to ultimate loads. Nevertheless, the reliability index of CSB-C36 was greater than that of CSB-C1 under the ULS,as shown in Fig. 17(a). This can be attributed to case 2 of the pattern loads,which induced more stress in CSB-C1 than in CSB-C36, causing a reduction in the reliability index of CSB-C1. Moreover, the fatigue effects were more critical for CSB-Cs located near the deck-tower connection in the CSB.

In the EDB case, two representative cables were selected (EDBC11 and EDB-C12) because these two cables undergo maximum live-to-dead load stress ratios. The reliability analysis results of these cables highlight the adequacy of the current safety factor of 1.67, yielding a reliability index greater than βt，u, as shown in Table 8.However,a safety factor lower than 1.67 yields a negative reliability index exceeding the ULS. For instance, the reliability indices of the stay cables EDB-C12 and EDB-C11 in the vector forms are[-7.4,4.12,17.16]and[3.09,6.08,9.58]under the ULS and FLS,respectively,at safety factors of[1.6,1.67,1.75].Similar to the CSBCs,the reliability index of the EDB-Cs along the EDB were also computed under the FLS and ULS, and the results are shown in Fig. 17(b), which reveals that a current safety factor of 1.67 yields reliability indices greater than βt，ufor the entire stay system of the EDB. Furthermore, EDB-Cs are more influenced by ultimate loads than by fatigue loads, and no significant variation was observed in the reliability indices of EDB-Cs along the EDB under the FLS owing to its high rigidity and redundancy. This is also because the stay cables of the EDB were considered as low fatigue extradosed cables.

4. Conclusions

The structural redundancies of a CSB and an EDB were compared through the safety assessment of stay cables under various loading conditions. Simplified FE models of both bridges were developed, and static analyses were performed. The redundancy was evaluated parametrically in terms of the DCR and reliability index by employing deterministic and nondeterministic approaches, respectively. The primary goal of this study was to describe the structural disparities between a CSB and an EDB and to verify their structural redundancies under the FLS and ULS.This goal was achieved through a parametric study of the safety factor of the stay cables of both bridges.Additionally,the effects of overloading, cable loss, and corrosion on the structural redundancy of both bridges were investigated in this study.The following conclusions were drawn based on the results of this research.

(1)The maximum effect of a single cable loss on the DCR of CSBCs occurs when the outermost cable of the bridge breaks,while the loss of two cables may have a significant effect on the DCR of CSBCs when a pair of stay cables breaks near the center the main span.

(2)The CSB is sufficiently redundant at a current safety factor of 2.5 under the FLS and ULS. Moreover, a safety factor of 2.2 yields minimum structural redundancy for a CSB under normal loading conditions; however, a CSB can lose its redundancy significantly at 2.2 in the case of an unexpected rupture/collapse of a stay cable.Therefore, a safety factor of 2.3 is essential to achieve the desired level of structural redundancy for CSBs.

(3)In the case of low fatigue EDB-Cs,the current safety factor of 1.67 yields a reasonably high redundancy under normal loading conditions. Nevertheless, this safety factor may not be sufficientto acquire enough structural redundancy for the entire stay system of an EDB in the case of an extreme damaging condition;therefore,a higher safety factor of EDB-Cs is indispensable for EDBs.

Table 7 Reliability analysis of CSB-C1 and CSB-C17 under ULS and FLS.

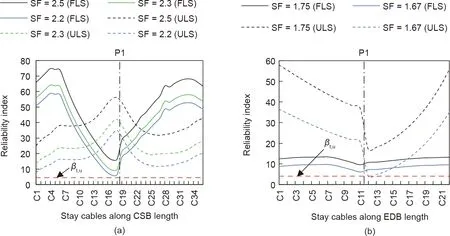
Fig. 17. Reliability analysis results by FORM under FLS and ULS. (a) CSB-Cs; (b) EDB-Cs.

Table 8 Reliability analysis of EDB-C12 and EDB-C11 under ULS and FLS.

(4) For a small change in the safety factor, the ultimate strengths of stay cables become more critical than their fatigue strengths. In particular, longer stay cables are extremely sensitive to this change in safety factors and loading conditions under the ULS.Thus,a significant increase in the reliability index occurs with an incremental increase in the safety factor of the stay cables of both bridges.

In this study, the cable loss was modeled as a static problem instead of a dynamic problem;therefore,an extension of this study is planned by incorporating the nonlinear dynamic-analysis-based cable loss model, which should provide more-comprehensive insights into the assessment of the structural redundancy of CSBs and EDBs.

Acknowledgements

This study was financially supported by the Ministry of Education, Culture, Sports, Science and Technology of Japan(Monbukagakusho (MEXT)).

Compliance with ethics guidelines

Khawaja Ali,Hiroshi Katsuchi,and Hitoshi Yamada declare that they have no conflicts of interest or financial conflicts to disclose.