高速列车通过隧道-桥梁-隧道时车体的气动效应

邓锷，杨伟超，何旭辉，王昂

（中南大学 土木工程学院，湖南 长沙，410075）

随着我国西部山区高速铁路建设的快速发展，高速铁路沿线中桥隧相连段已成为峡谷两侧最常见的基础设施场景[1-2].如兰渝线以及沪昆线贵州段，桥梁与隧道占线路总长的比例可达70%～80%.由于峡谷地形对气流的特殊作用，当高速列车运行至桥隧相连段或完全运行于桥梁上时常遭遇强横风[3].为同时保证列车运行安全和桥梁结构的稳定性，开孔式风屏障逐渐在该地区桥梁上推广应用.

近年来，国内外诸多学者围绕桥上风屏障的防风性能展开一系列研究.何旭辉[4-5]等通过风洞试验研究了一种百叶窗型风屏障对车桥系统气动特性的影响，并针对风屏障参数进行了优化.Xiang 等[6]和项超群等[7]研究了不同风屏障高度对运行于桥上的列车气动荷载的影响，结果表明列车气动荷载随风屏障高度增加而减小，风屏障高度为4 m 时比没有设置风屏障时列车各项气动荷载系数减小40%～50%.何玮等[8]研究了风屏障透风率对横风下大跨度斜拉桥车-桥耦合振动的影响，结果表明车辆和桥梁的动力响应均随透风率的增大而增大.Olmos 等[9]和郭薇薇等[10]分析了风屏障对车桥系统气动效应及桥上高速行驶车辆运行安全性的影响.可见，上述研究主要是针对高速列车完全运行于桥上风屏障区段时的气动性能及行车安全，并未涉及列车运行过程中基础设施场景的转换.张田等[11]研究发现横风环境中桥上高速列车进出风屏障时，风载突变对车体横向振动响应有显著影响.事实上，Yang 等[12-14]研究发现高速列车在横风环境下驶入（驶出）隧道时，车身同样会出现剧烈的气动突变效应，严重威胁列车运行安全.因此，当高速列车在横风环境中运行于桥隧相连段时，该区段风屏障的防风性能尤为关键.

为此，本文以我国高速铁路沿线上某座典型的隧道-桥梁-隧道基础设施为工程背景，基于计算流体力学和多孔介质理论建立了列车-隧道-桥梁-风屏障-空气三维CFD 数值仿真模型；然后以列车运行于该设施全过程的瞬态气动荷载系数为对象，研究了其变化特性；最后针对横风环境中列车运行于桥隧相连段的过程（由隧道驶入桥梁或由桥梁驶入隧道），从流场角度进一步揭示了风屏障的存在与否对气动荷载突变效应的影响.所得结论有望为我国高速列车运行至隧-桥-隧基础设施时的行车安全指挥进一步提供理论依据.

1 基本理论

1.1 湍流模型

根据本文工况特点可推测：列车周围流场马赫数（Ma）小于0.3，雷诺数（Re）大于106.因此可认为本文所涉及的流体是不可压缩且处于高度湍流状态的.基于此，本文采用RNG k-ε 两方程湍流模型[15-17]来模拟列车周边流场结构的瞬态演化过程.

1.2 多孔介质参数计算

本文开孔式风屏障采用多孔介质模型进行模拟，即在流体动量方程中增加一个代表动量消耗的源项.该源项由两部分组成，即Darcy 黏性阻力项和惯性损失项.对于简单的均匀多孔介质，动量源项可表达为：

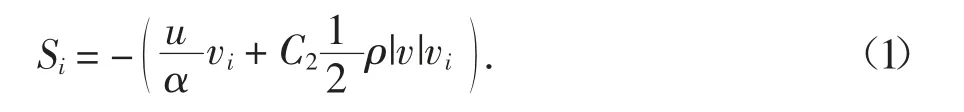
式中：|v|是速度的绝对值；C2是惯性阻力系数；α 是渗透系数.

在高速流场中模拟多孔板时，只使用惯性损失系数便可得到多孔介质压降方程（渗透项可忽略）：

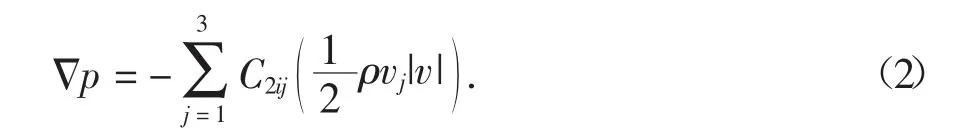
阻力系数的计算常采用经验公式：

式中：ν 是表观速度.

将式（4）与式（2）比较可得在垂直于板方向的阻力系数C2：

2 数值模型

2.1 几何模型及边界条件

列车模型采用我国高速铁路常用的CRH3 型列车.建模时，对实际列车的几何模型进行了一定程度的简化，忽略转向架、车顶受电弓以及车窗等部件（如图1 所示），采用3 节编组，全长约76 m.桥梁几何模型采用我国高速铁路沿线中使用频率最高的混凝土简支箱梁，如图2 所示.桥长159 m，桥面宽12.0 m，高3.05 m.不考虑桥面轨道结构及桥墩的影响.列车底部与桥面距离取0.2 m.风屏障在全桥范围内设置，厚0.1 m，高3 m，透风率30%.桥梁两端分别与2座双线隧道连接，隧道长均为200 m，净空面积均为100 m2.

图1 列车几何模型Fig.1 Train geometric model

整体计算区域如图2（a）所示.车头鼻尖初始位置（t=0 s）距隧道1 入口约80 m，车速设置为250 km/h.隧道1 两端外部大气场属于半无限空间，采用半柱体模拟.其中，隧道1 入口外端为平坦地面，相应大气场直径约38 m，长200 m，无横风作用，采用Pressure-oulet 边界条件；桥梁区段大气场直径约240 m，采用Pressure-far-field 边界条件，横风风速设置为25 m/s，且垂直于列车运行方向.隧道2 出口处也采用Pressure-oulet 边界条件.列车表面、隧道的壁面、桥梁表面及地面均设置成无滑移壁面边界（Wall）.

图2 计算区域及边界条件Fig.2 Calculation region and boundary conditions

2.2 网格策略及计算

基于ANSYS ICEM，采用六面体结构化网格将整个计算区域划分为3 个区域，即动网格区域、静网格区域和多孔介质区域，如图3 所示.其中，静网格区域保持静止，动网格区域包含列车及其附近的空气，运用铺层法[16-17]实现列车与地面的相对运动.区域之间的流场数据通过组建Interface 对进行传递.考虑到车身周围流场的附面层效应，在车、桥和风屏障的表面分别设置10 层、10 层和8 层附面层网格，第1 层网格厚度设为1×10-3m，相应的y+值接近30.列车表面的网格尺寸约为0.02～0.05 m.模型总网格单元数约3 200 万.将模型导入ANASYS FLUENT 进行计算，物理时间步长设为1×10-3s.

图3 网格模型Fig.3 Grid model

3 气动荷载系数计算

单节车厢5 项气动荷载（即气动横向力Fz、气动升力Fy、倾覆力矩Mx、偏航力矩My和点头力矩Mz）的计算方法可参照文献[15].相应的无量纲化计算公式如下：

式中：CP为气动压力系数；P 表示车厢表面上的气动压力；P∞表示无穷远处的静压；Ci（i=z，y）表示气动力系数；Cmi（i=x，y，z）表示气动力矩系数；ρ 表示空气密度；Va表示相对于列车的合风速（图4（c））；A 和h 分别表示单节车厢的侧面积和特征高度.

图4 CRH3 型列车模型与ICE3 型列车模型的尾车外型对比Fig.4 Comparison of rear carriage shape between the CRH3 model and the ICE3 model

4 模型验证

4.1 网格独立性检查

为检查网格独立性，通过改变模型网格尺寸分别建立粗（1 600 万）、中（3 200 万）、细（4 800 万）3 种具有不同网格单元数的模型.以列车运行于平地时各节车厢的最大横向力（Fz，max）为监测指标，横风风速为25 m/s，车速为250 km/h.图5 对比了3 个模型的监测指标值.结果表明，网格单元数为3 200 万的模型与单元数为4 800 万的模型计算结果吻合较好.因此，采用具有3 200 万网格单元数的模型是合理的.

图5 不同网格分辨率条件下各节车厢最大横向力Fig.5 The maximum side force of each carriage under different mesh resolution conditions

4.2 结果验证

为验证本文数值模型结果的可靠性，将Schober[18]采用ICE3 型（其外型与中国的CRH3 型列车高度一致）1 ∶15 缩尺模型（见图4）进行风洞试验所得的尾车气动荷载数据与本文相应的数值模拟结果进行对比.为确保本文工况的雷诺数可被该试验验证所涉及的雷诺数范围所覆盖（本文工况的最大合风速为73.8 m/s，风向角β 约为20°），验证过程中将列车运行速度Vt和风速Va分别设定为0 km/h 和78 m/s.式（6）中参数A 和h 分别取为10 m2和3 m.最后计算不同β（15°，20°，30°，45°和60°）条件下尾车的气动横向力系数Cz与偏航力矩系数Cmy，如图6 所示.

由图6 分析可知，本文数值计算结果与Schober的试验结果变化趋势基本一致.除个别数据相差稍大之外，其余的数值计算结果与试验结果基本吻合，相差保持在10%以内.因此，可认为本文CFD 数值模型及其计算结果是可靠的.

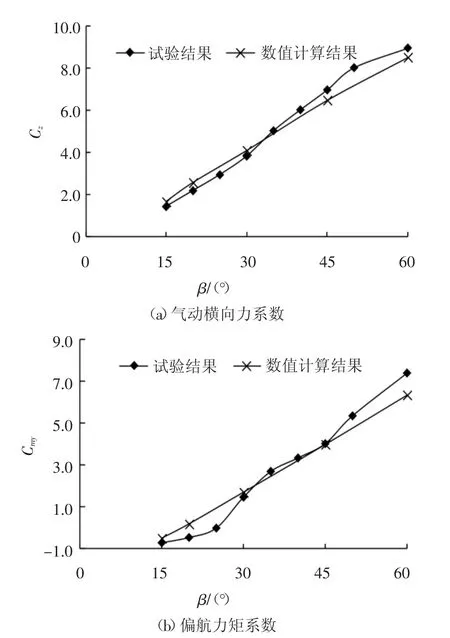
图6 结果对比Fig.6 Comparison of results

5 结果分析

5.1 气动荷载

图7 给出了在25 m/s 的横风环境下，列车以速度250 km/h 运行于隧道-桥梁-隧道基础设施过程中，3 节车厢的气动横向力、升力系数以及倾覆力矩、偏航力矩和俯仰力矩系数时程曲线在有无风屏障条件下的对比.图中“出”表示车头鼻尖驶出隧道1至车尾鼻尖驶入桥梁的过程（t=4.03～5.13 s）；“进”表示车头鼻尖驶入隧道2 至车尾鼻尖驶离桥梁的过程（t=6.32～7.42 s）.根据Deng 等[13]的研究，车厢所受的气动荷载在极短时间内的大幅度波动将显著提高列车运行的安全风险.因此，表1 给出了对应于图7 的各节车厢分别在“出”和“进”过程中的气动荷载系数最大波动幅度的对比.

图7 有无风屏障条件下各节车厢气动荷载系数时程曲线对比Fig.7 Comparison of time history curves of aerodynamic load coefficients of each carriage with or without wind barrier

由图7 和表1 分析可知：

表1 有无风屏障条件下气动荷载系数突变幅度对比Tab.1 Comparison of sudden change amplitudes of aerodynamic load coefficients with or without wind barrier

1）在无风屏障条件下，列车各节车厢的气动荷载系数在“出”和“进”的过程中均表现出显著的“脉冲”现象（即瞬间加载和卸载，这一现象与文献[13]和[14]中所报道的类似）.说明高速列车在横风环境下运行于隧道-桥梁-隧道基础设施时，若桥上没有设置风屏障，过程“出”和“进”的运行安全风险将显著高于其他时段.

2）在有风屏障条件下，列车各节车厢的气动荷载系数在“出”和“进”的过程中的波动幅度均出现显著下降.以头车为例，横向力、升力、倾覆力矩、偏航力矩和俯仰力矩系数波动幅度在“出”过程中分别下降了86%、82%、80%、59%和36%；在“进”过程中分别下降了87%、83%、83%、61%和61%.

3）无论在“出”或“进”的过程中，风屏障条件下，各节车厢的横向力波动幅度下降率相对于其余4 项气动荷载均是最为突出的（如，头车、中间车和尾车在“出”过程中分别高达86%、95%和87%；在“进”过程中分别高达87%、95%和89%）.中间车的气动升力系数以及3 节车厢的俯仰力矩波动幅度下降率相对较小.说明运行于桥隧相连段时的列车气动横向力的变化对风屏障的影响最为敏感，而俯仰力矩的敏感性相对较弱.

4）在无风屏障条件下，列车各节车厢在“进”过程的气动荷载波动幅度大于“出”过程的相应值.用比值“进/出”来量化它们之间的差异可知：头车、中间车和尾车在“进”过程的气动横向力、升力、倾覆力矩、偏航力矩和俯仰力矩的波动幅度分别是“出”过程中相应值的1.03、1.06、1.20、1.03 和1.64 倍，1.03、1.22、1.00、1.04 和1.89 倍以及1.16、1.50、1.00、1.03和1.88 倍.而在有风屏障的条件下，列车各节车厢的“进/出”值基本为1.说明风屏障的存在，将明显削弱“列车各节车厢在‘进’过程的气动荷载波动幅度大于‘出’过程的相应值”这一特征.

5.2 由隧到桥过程的流场及压力

本节将从流场角度进一步揭示列车在25 m/s 横风环境中由隧道1 驶入桥梁过程中气动荷载突变现象以及风屏障对气动荷载突变的影响机制.图8 以轨道顶面上方1.5 m 高度处（Y=1.5 m）的水平面为例，分别给出了有无风屏障条件下列车以速度250 km/h 由隧道1 驶入桥梁过程中周围流场变化.图9给出了对应过程的车身表面压力系数分布.图中（a）表示车头鼻尖抵达隧道1 出口的时刻（即t=4.03 s）；（b）（t=4.40 s）、（c）（t=4.76 s）和（d）（t=5.13 s）分别表示头车、中间车和尾车完全驶出隧道1 的时刻.

由图8 和图9 分析可知：

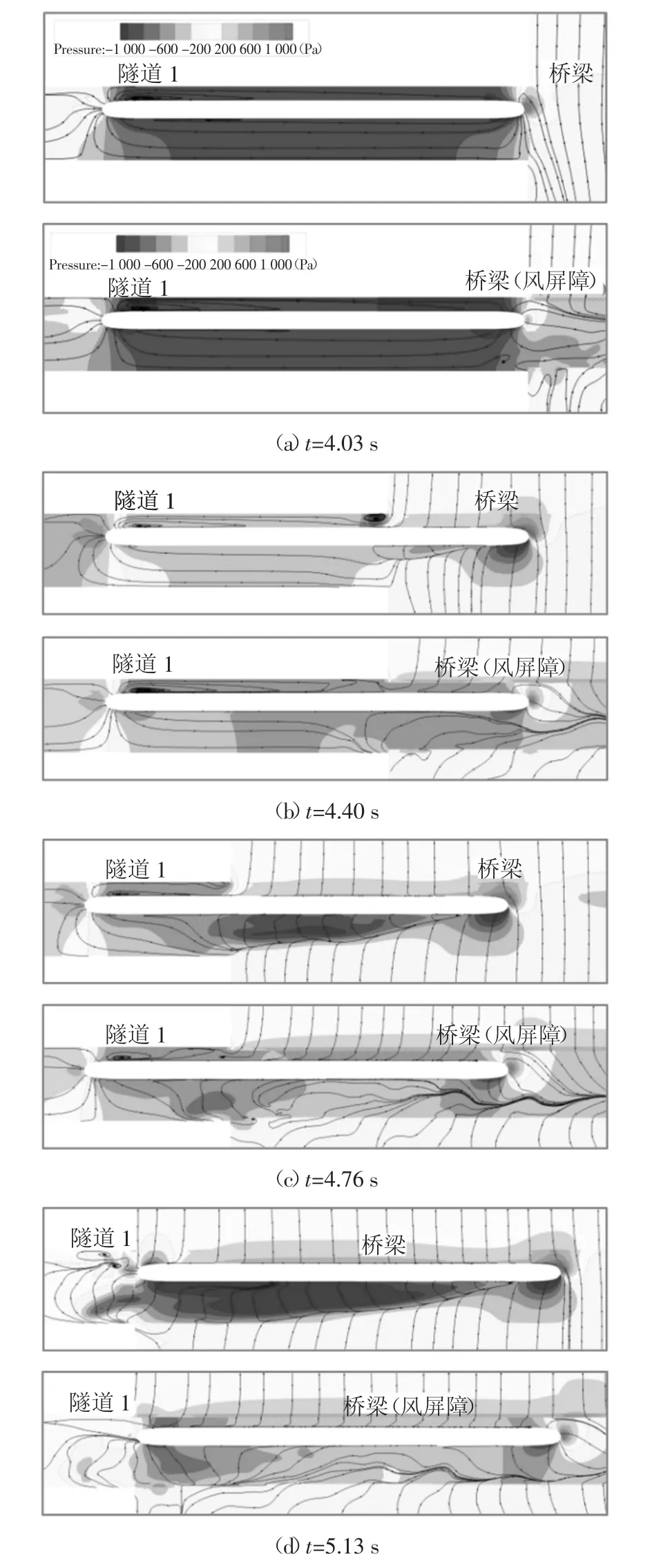
图8 有无风屏障条件下列车由隧道1 进入桥的过程中Y=1.5 m 水平面上流场演化Fig.8 Flow field evolution on the horizontal plane Y=1.5 m in the process of train entering bridge from tunnel 1 with or without wind barrier

1）无论风屏障的有无，对于隧道内部分车体，其周围流场结构和车身压力分布在不同的时刻均表现出相似的特征.即：车身两侧气流方向与列车运行方向相反，向车尾鼻尖处汇集；车身两侧压力基本对称，且均表现为负压，压力值大小也基本相等.说明桥上风屏障对隧道1 内的流场和压力变化基本没有影响.

2）对桥上部分车体，在无风屏障条件下，车身背风侧在横风和列车风联合作用下逐步形成纵向喇叭状涡流，涡流区对应为负压区，相应的背风侧车体表面也受到沿纵向（与运行方向相反）递增的负压（如图9（c）和（d）中85～120 m 区段）；对应的迎风侧平直车身表面则在横风的正面挤压作用下受沿纵向均匀分布的正压（压力系数保持在0.1 左右）；车身两侧压差在车头鼻尖处最为显著（最大正压系数达0.4，最大负压系数达-0.6）.在有风屏障条件下，桥上部分车体背风侧不再出现喇叭状纵向涡流；部分流线透过两侧风屏障，在车身背风侧汇集并流向前方；除车头鼻尖前方区域的空气由于受到挤压而呈现正压之外，车身两侧在不同时刻均受基本对称的负压（如图9（b）（c）（d））.

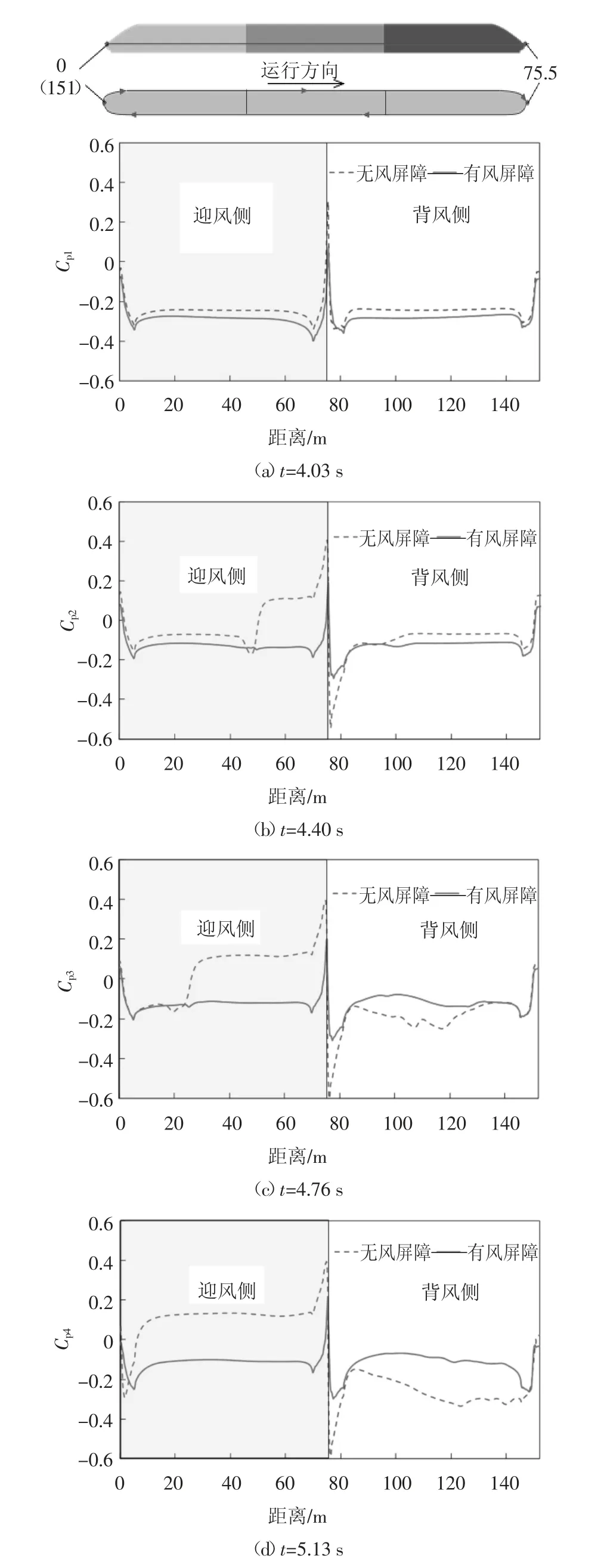
图9 有无风屏障条件下列车由隧道1 进入桥过程的车体表面压力系数Fig.9 The pressure coefficient on the train surface in the process of entering the bridge from tunnel 1 with or without wind barrier

综上所述，列车由隧道1 驶入桥梁过程中，当存在风屏障时，桥上部分车体周围原有的流场结构特征发生改变，两侧所受负压均匀且基本对称，从而导致各节车厢气动荷载在“出”过程中波动幅度显著减小；又因风屏障主要引起车身两侧压差的改变，因此横向力的变化对风屏障的影响最为敏感.

5.3 由桥到隧过程的流场及压力

图10 给出了有无风屏障条件下列车以速度250 km/h 由桥梁驶入隧道2 过程中周围流场变化.图11给出了对应过程的车身表面压力系数分布.图中（a）表示车头鼻尖抵达隧道2 入口的时刻（即t=6.32 s）；（b）（t=6.69 s）、（c）（t=7.05 s）和（d）（t=7.42 s）分别表示头车、中间车和尾车完全驶入隧道2 的时刻.

由图10 和图11 分析可知：

1）桥上风屏障对隧道2 内车体周围的流场以及车身压力变化仍基本无影响.具体表现为：无论风屏障的有无，车头鼻尖处流场均呈现出源流特性，部分气流沿车身与隧道2 之间的空隙于隧道入口处喷出，形成喷射流；隧道内车身两侧压力沿纵向分布均匀，压力值基本相等.

2）对于桥上部分车体，在无风屏障条件下，附着于车身背风侧的纵向喇叭状涡流在喷射流抑制作用下终止于隧道2 入口处；尚存部分涡流的原有结构在喷射流的干扰下也发生了一定程度的改变，从而导致背风侧车身表面负压增大（如图11（b）（c）所示）；而迎风侧的喷射流由于与横风联合作用产生了竖向涡流而消散于隧道2 入口处（如图10（b1）（c1）（d1）所示），故桥上迎风侧平直车身表面的正压系数仍保持在0.1 左右.说明无风屏障条件下，列车各节车厢在“进”过程的气动荷载波动幅度大于“出”过程的相应值的主要原因可能是列车驶入隧道2 时产生的喷射流对背风侧纵向涡流的干扰作用.

图10 有无风屏障条件下列车由桥进入隧道2 的过程中Y=1.5 m 水平面上流场演化Fig.10 Flow field evolution on the horizontal plane Y=1.5 m in the process of train entering tunnel 2 from bridge with or without wind barrier

图11 有无风屏障条件下列车由桥进入隧道2过程的车体表面压力系数Fig.11 The pressure coefficient on the train surface in the process of entering the tunnel 2 from bridge with or without wind barrier

3）在有风屏障条件下，横风对于风屏障内侧车身两侧的流场结构的干扰明显减弱.因此桥上部分车身两侧压力分布在不同时刻仍保持基本对称，从而导致各节车厢气动荷载在“进”过程中波动幅度显著减小.

6 结论

1）列车在25 m/s 横风环境中以车速250 km/h运行于桥隧相连段时，无风屏障条件下各节车厢的气动荷载均表现出显著的“脉冲”现象；若桥上设置高3 m、透风率为30%的风屏障，相应的各项气动荷载突变幅度将减少36%～95%.

2）由于风屏障主要引起车身两侧压差的改变，运行于桥隧相连段时的列车气动横向力的变化对风屏障的影响最为敏感，而气动升力和俯仰力矩的敏感性相对较弱.

3）无风屏障条件下，由于列车驶入隧道时引发的喷射流对列车背风侧纵向涡流有干扰作用，各节车厢在“由桥至隧”过程的气动荷载波动幅度是“由隧至桥”过程中相应值的1.03～1.89 倍；若桥上设置风屏障，两过程中气动荷载波动幅度基本相等.