长周期地震动的能量反应谱

李宇，李琛，赵福志，李钊

（1.长安大学 公路学院，陕西 西安 710064；2.长安大学 建筑学院，陕西 西安 710064）

2003 年，在日本十胜冲地震中，苫小牧地区（震中距约225 km，PGA=89.2 gal）的储油罐被破坏并引发火灾；北海道许多桥梁也发生破坏，如Rekifune Bridge 跨中竖向位移达12 cm.2011 年，在东日本大地震中，东京都办公大楼（震中距约300 km）地下3层的最大加速度仅为74 gal，而顶部（48 层）最大位移却达65 cm；大阪府办公大楼（震中距约700 km）顶部（52 层）最大加速度仅为131 gal，而最大位移却达132 cm.可见，长周期地震动（远场卓越周期偏大型地震动）对长周期结构有较大影响.此后，学者们开始真正地关注长周期地震，并研究了长周期地震作用下的超高层建筑结构[1-5]、基础隔震结构[6-7]、隔震桥梁[8]、钢筋混凝土框架[9-10]和风电机组[11]等长周期结构的地震响应.但是，上述研究仅停留在计算长周期结构地震响应的初步阶段，还未能在长周期地震作用下进行长周期结构的抗震设计.究其原因，主要是由于缺乏抗震设计用的长周期地震反应谱.

目前，反应谱法仍是世界各国抗震规范中最主要的抗震设计方法，而反应谱则是该法的基础.随着长周期结构的日益增多，我国《建筑抗震设计规范》（GB 50011—2010）[12]、《铁路工程抗震设计规范》（GB 50111—2006）[13]和《公路桥梁抗震设计规范》（JTGT 2231-01—2020）[14]分别将反应谱延伸至6 s、5Tg和10 s，但仍未能满足工程应用要求，而且反应谱下降段也与实际长周期反应谱的特征不符（即特征周期Tg偏小、下降形式单一和幅值偏小）[15].因此，有必要针对长周期反应谱开展专门研究.

由于传统地震仪的缺陷和大震级地震发生的概率较小，记录到的长周期地震动时程并不多[15].因此，针对长周期地震动反应谱的研究还很少：张亮泉等[15]、李宇等[16]、Zhou 等[17]对长周期地震的弹性、弹塑性加速度和位移反应谱等进行了初步探索；陈清军等[18]则选取了36 条长周期地震动记录，对长周期地震的能量谱进行了研究.但是，由于他们所依据的长周期地震动记录的数量太少，所得研究结果不具有统计意义，而且也没有详细讨论长周期地震的非弹性能量反应谱.因此，本文通过对比长周期和常规地震动的特性，选取139 条长周期地震动记录作为输入，以期建立长周期地震动的弹性和非弹性输入能量设计谱.

1 长周期地震动的特征

长周期地震动（台湾集集地震的TCU018 和TCU094）和常规地震动（El Centro 波和天津波）的加速度时程（t 为时间，a 为加速度）如图1 所示.通过傅里叶变换，可得其傅里叶幅值谱（如图2 所示，f 为频率，B 为幅值），可知：常规地震动的卓越频率分布较宽，且集中在高频（1～5 Hz）；而长周期地震动的卓越频率分布较窄，且集中在低频（0.1～1.0 Hz）.

将4 条地震动按同一PGA 调幅后，对比它们的弹性加速度和位移反应谱（Sat为加速度谱值，D 为位移谱值，T 为周期），从图3 可知：在长周期段，长周期地震动的谱值要远大于常规地震动，即长周期地震动对长周期结构（如大跨桥梁、超高层建筑）的影响很大.

图2 长周期和常规地震动的频率对比Fig.2 Comparison of the frequency of the long-period and conventional ground motions

图3 长周期和常规地震动的反应谱对比Fig.3 Comparison of the response spectra of the long-period and conventional ground motions

2 长周期地震动的选取

根据长周期地震动记录的挑选标准[16-19]：震中距较大；卓越频率分布较窄，且集中在0.1～1.0 Hz 的低频段；弹性加速度反应谱的峰值在中长周期段.从PEER、K-NET 和KIK-NET 中挑选了139 条长周期地震动记录（6 级以上），并采用地震动数据处理软件SeismoSignal 进行了滤波处理与基线校正，进而计算相关地震动参数.

根据文献[20]：美国抗震设计规范的vs30（覆盖层厚度为30 m 的剪切波速）≥510 m/s、260 m/s ≤vs30<510 m/s、150 m/s ≤vs30<260 m/s、vs30<150 m/s 的场地分别对应中国抗震设计规范[12-14]的场地SiteⅠ～Ⅳ.因此，可将139 条长周期地震动记录按中国抗震设计规范[12-14]的场地标准进行分类，见表1：Site Ⅰ有38 条，Site Ⅱ有40 条，Site Ⅲ有41 条，SiteⅣ有20 条.

再以139 条长周期地震动记录作为激励，计算Ⅰ～Ⅳ类场地的动力放大系数β（阻尼比ξ=5%，周期为T），并与规范[14]的β 曲线进行对比（见图4），从中可知：统计所得的β 曲线与规范值符合较好.可见，本文所选用的长周期地震动记录符合规范要求.

图4 β 的对比Fig.4 Comparison of β

2 非弹性地震能量谱的基本原理

将式（1）对x（t）积分，则[22]：

表1 选取的长周期地震动记录Tab.1 Selected long-period ground motion records

式中：k1为恢复力模型初始刚度.

再定义滞回耗能比λH和阻尼耗能比λD，以评价系统的滞回耗能能力和阻尼耗能能力，即：

在地震作用下，计算具有不同周期T、阻尼比ξ和位移延性比μ 的非弹性SDOF 体系的各类能量响应的最大值，进而绘制输入能量谱SEI、滞回耗能谱SEH、阻尼耗能谱SED、滞回耗能比谱SλH、阻尼耗能比谱SλD[18].则对于单位质量（m=1）的非弹性SDOF 体系，有：

注意：当非弹性SDOF 体系的m≠1 时，以上各能量谱值应乘以m 后，才能得到各类能量响应.

下文将考虑周期（T=0.01～20 s）、恢复力模型、屈服后刚度比（η=k1/k2=0.0～0.05，k2为二次刚度）、位移延性比（μ=xmax/xy=l.0～5.0，xmax为最大位移，xy为屈服位移）、阻尼比（ξ=2%～14%）、震级（MW）、场地、地震峰值加速度（PGA）的影响，利用BISPEC 程序，研究长周期地震的非弹性能量谱（SEI、SEH、SED、SλH、SλD）.

3 恢复力模型参数的影响

3.1 恢复力模型

以Ⅱ类场地为例，将40 条长周期地震动记录的PGA 调幅为0.15g，采用考虑刚度退化的Takeda 模型和无刚度退化的双线性模型（图5），并取η=0.05、ξ=5%、μ=1.0～5.0，采用BISPEC 计算SEI、SEH、SED、SλD、SλH的平均值.

图5 恢复力模型Fig.5 Restoring force models

从图6 可知，当μ 相同时：1）无刚度退化模型的能量谱峰值平台段要长于刚度退化模型的能量谱峰值平台段，而且无刚度退化模型的特征周期也要大于刚度退化模型的特征周期；2）在中短周期段，无刚度退化模型的能量谱值要小于刚度退化模型的能量谱值，而在中长周期段则反之.可见，相比于刚度退化模型，无刚度退化模型能量谱的峰值平台、特征周期和中长周期段谱值都要长或大，即采用无刚度退化模型的能量谱值对长周期结构进行抗震设计，会偏于保守.

从图7 可知，当μ 相同时，在中短周期段，2 种模型的SλH和SλD的谱值差距较大，但随着T 的增加，SλH和SλD的谱值逐渐趋于一致.可见，长周期结构的周期越长，恢复力模型对塑性铰滞回耗能能力和系统阻尼耗能能力的影响就越小.

图6 恢复力模型对长周期地震能量反应谱的影响Fig.6 Effect of restoring force models on the energy response spectra of the long-period ground motions

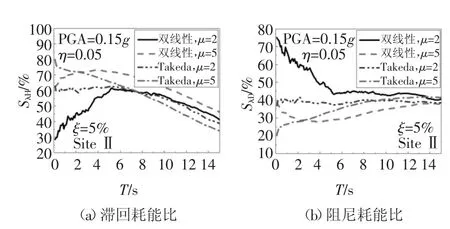
图7 恢复力模型对SλH 和SλD 的影响Fig.7 Effect of restoring force models on the SλH and SλD

文献[23]研究了恢复力模型对常规地震能量谱的影响，与本文的研究结果对比后可知：

1）恢复力模型对常规地震能量谱的影响随着μ的增加而减小，特别是当μ>5 后，恢复力模型的影响可以忽略；但是，恢复力模型对长周期地震能量谱的影响则随着μ 的增大而越加显著.

2）不同恢复力模型对应的常规地震能量谱的峰值平台段的长度和位置没有太大区别；但是，相比于双线性模型，Takeda 模型的长周期地震能量谱的峰值平台段的长度更短而且更靠后（原点方向）.

3.2 屈服后刚度比

以I 类场地为例，将38 条长周期地震动记录的PGA 调幅为0.15g，采用Takeda 模型，取μ=1.0～5.0、ξ=5%，采用BISPEC 计算η=0、0.025、0.05 的SEI、SEH、SED、SλD、SλH的平均值.

从图8、图9 可知：当μ 相同时，η 对SEI、SEH、SED、SλD、SλH的影响可以忽略，即在统计长周期地震能量反应谱时，可以不考虑η 的影响.

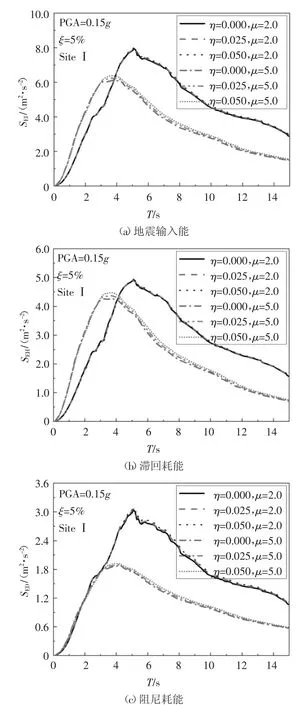
图8 η 对长周期地震能量反应谱的影响Fig.8 Effect of η on the energy response spectra of the long-period ground motions

图9 η 对SλH 和SλD 的影响Fig.9 Effect of η on the SλH and SλD

文献[24]研究了η 对常规地震能量谱的影响，从中可知：η 对常规地震的能量谱谱值的影响很小.这与η 对长周期地震的能量谱的影响结论相同.可见，无论是何种类型的地震动，η 对地震能量谱的影响都是可以忽略的.

芬兰财政部近日预测，2018年芬兰经济增长率为2.5%，2019年将放缓至1.5%。芬兰央行预测，2018年芬兰经济增长率为2.7%，2019年将放缓至1.9%，2020年将进一步降至1.7%。芬兰经济的高速增长期已经过去，现在应该采取预防性措施，为今后可能出现衰退做好应对准备。分析人士认为，经济增长放缓将导致税收减少，从而影响当前芬兰政府的庞大福利开支。如何在维持目前公共开支水平的同时，保持政府可持续运转，将是芬兰政府今后面临的首要任务。

3.3 阻尼比

以I 类场地为例，将38 条长周期地震动记录的PGA 调幅为0.15g，采用Takeda 模型，取η=0.05，μ=l.0～5.0，采用BISPEC 计算ξ=2%、5%、10%、14%时的SEI、SEH、SED、SλD、SλH的平均值.

从图10、图11 可知：随着ξ 增大，SEI峰值、SEH和SλH都逐渐减小，SEI长周期段谱值、SED和SλD都逐渐增大，而SEI峰值平台长度和特征周期则变化较小.可见，ξ 的增大，对SEI有削峰作用，并会增大SEI长周期段谱值，但不改变SEI峰值平台长度和特征周期；另外，随着ξ 增大，塑性铰的滞回耗能能力降低，而系统的阻尼耗能能力提高.

图10 ξ 对长周期地震能量反应谱的影响Fig.10 Effect of ξ on the energy response spectra of the long-period ground motions

图11 ξ 对SλH 和SλD 的影响Fig.11 Effect of ξ on the SλH and SλD

文献[24]研究了ξ 对常规地震能量谱的影响，与本文的研究结果对比后可知：ξ 对常规地震和长周期地震的SEH和SED影响相同（随着ξ 增大，不同类型地震的SEH减小而SED增大）；但是，ξ 对不同类型地震的SEI长周期段的影响则不同（随着ξ 增大，常规地震的SEI的长周期段的谱值减小，而长周期地震的SEI的长周期段的谱值则增大）.

3.4 位移延性比

以Ⅱ类场地为例，将40 条长周期地震动记录的PGA 调幅为0.30g，采用Takeda 模型，取η=0.05、ξ=5%，采用BISPEC 计算μ=1.0～5.0 时的SEI、SEH、SED、SλD、SλH的平均值.

从图12 可知：随着μ 的增大，SEI和SED的峰值减小，SEH峰值变化较小，SEI和SEH的峰值平台段增长，并往短周期方向移动，它们的特征周期也相应减小.可见，μ 的增大，对SEI和SED有削峰作用，并使SEI和SEH的峰值平台段往短周期方向移动，并减小它们的特征周期.

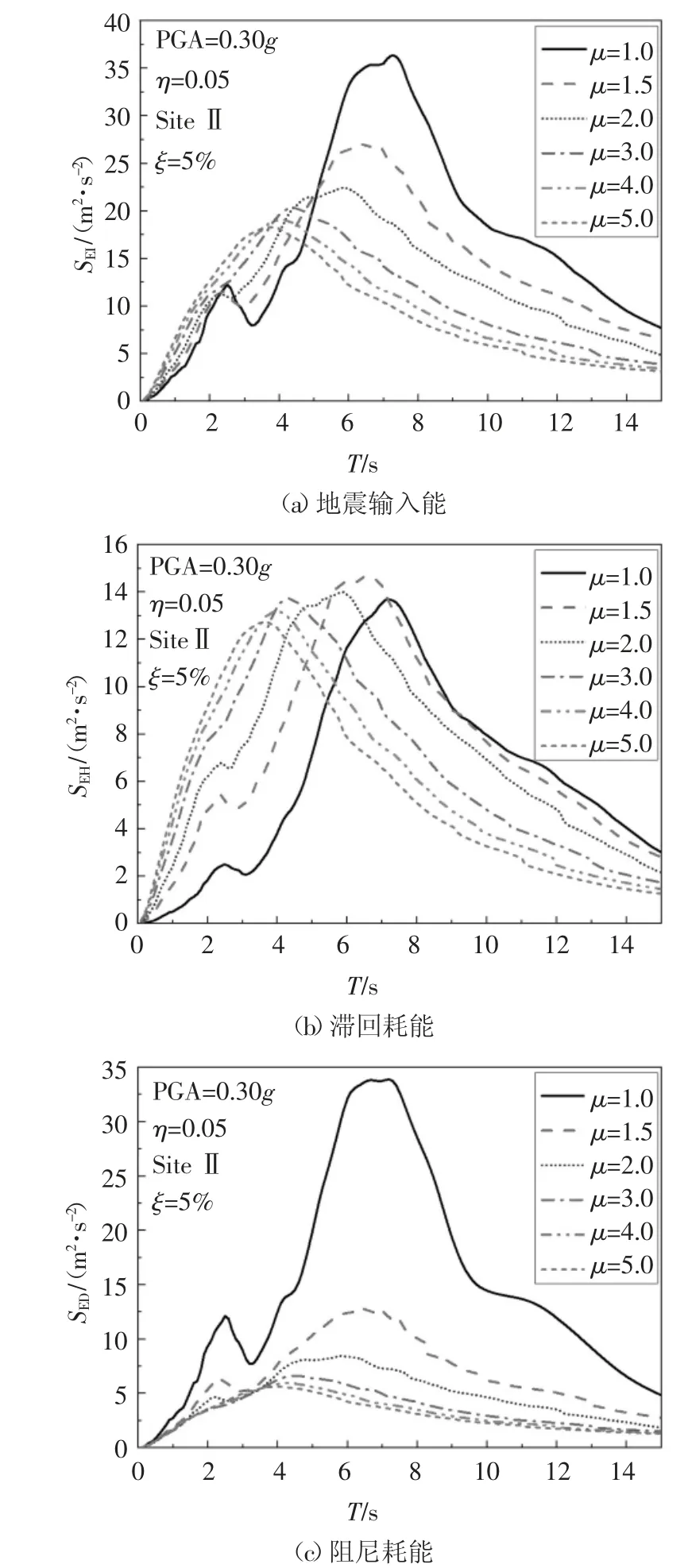
图12 μ 对长周期地震能量反应谱的影响Fig.12 Effect of μ on the energy response spectra of the long-period ground motions

从图13 可知，当其他条件相同时，在中短周期段，随着μ 的增大，SλH增大而SλD则减小；但随着T的增加，SλH和SλD的谱值逐渐趋于一致.可见，随着μ的增加，塑性铰的滞回耗能能力都提高，而系统的阻尼耗能能力则降低；另外，长周期结构的周期越长，μ对塑性铰滞回耗能能力和系统阻尼耗能能力的影响就越小.

图13 μ 对SλH 和SλD 的影响Fig.13 Effect of μ on the SλH and SλD

文献[24]研究了μ 对常规地震能量谱的影响，与本文的研究结果对比后可知：μ 对常规地震和长周期地震的SEI和SED的影响规律相同（随着μ 增大，SEI和SED都逐渐减小），但对与μ 联系最紧密的SEH的影响规律则不同（随着μ 增大，常规地震的SEH的峰值平台段后移（往原点方向））、平台段缩短、峰值增大，相反地，长周期地震的SEH的峰值平台段后移、平台段延长、峰值降低）.

4 地震动特性的影响

4.1 震级

从图14 可知，随着MW的增大，SEI、SEH、SED随之增大.这是因为MW越大，地震释放的能量就越多，使得结构地震能量响应也越大.

图14 MW 对长周期地震动能量反应谱的影响Fig.14 Effect of MW on the energy response spectra of the long-period ground motions

从图15 可知：随着MW的增大，SλH减小而SλD增大.可见，MW越大，结构的损伤也就越大，塑性铰的滞回耗能能力下降，结构将主要依靠阻尼来消耗地震能量.

图15 MW 对SλH 和SλD 的影响Fig.15 Effect of MW on the SλH and SλD

4.2 场地

将139 条长周期地震动记录的PGA 调幅为0.30g，采用Takeda 模型，取η=0.05、ξ=5%、μ=3.0，采用BISPEC 计算I、Ⅱ、Ⅲ、Ⅳ类场地的SEI、SEH、SED、SλD、SλH的平均值.

从图16 可知：随着场地土质的变软，SEI、SEH、SED随之增大.这是因为场地土越软，场地与长周期地震动的卓越周期就越接近，进而导致结构地震能量响应的放大.

从图17 可知：随着场地土变软，SλH减小而SλD增大.可见，场地土越软，塑性铰的滞回耗能能力就越低，而系统的阻尼耗能能力则提高.

图16 场地对长周期地震能量反应谱的影响Fig.16 Effect of the site classification on the energy response spectra of the long-period ground motions

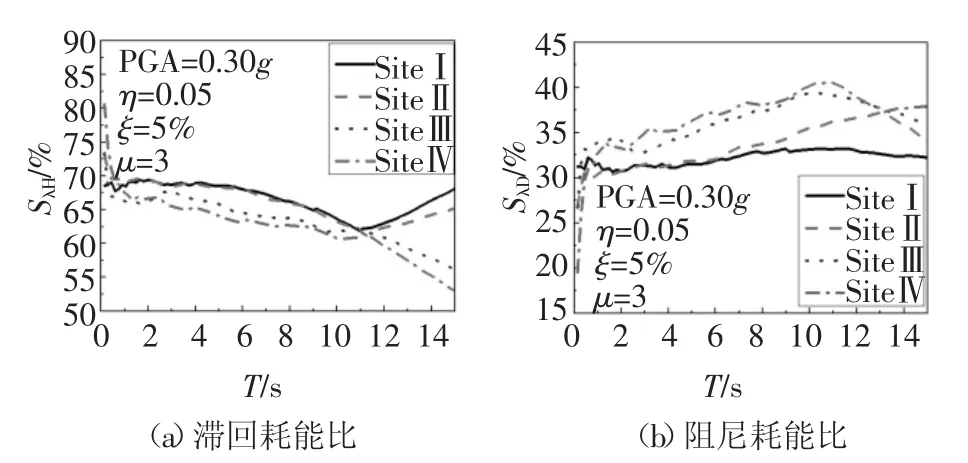
图17 场地对SλH 和SλD 的影响Fig.17 Effect of the site classification on the SλH and SλD

4.3 PGA

以Ⅱ类场地为例，将40 条长周期地震动记录的PGA 分别调幅为0.05g、0.10g、0.30g 和0.40g，采用Takeda 模型，取η=0.05、ξ=5%、μ=1.0～5.0，采用BISPEC 计算SEI、SEH、SED、SλD、SλH的平均值.

从图18、图19 可知：随着PGA 的增大，SEI、SEH、SED随之增大；同一PGA 下，随着μ 的增大，SEI、SEH、SED逐渐减小；若结构的μ 相同，则可忽略PGA 对SλH和SλD的影响；另外，若以0.10g 的SEI为基准，则：

图18 PGA 对长周期地震能量反应谱的影响Fig.18 Effect of the PGA on the energy response spectra of the long-period ground motions

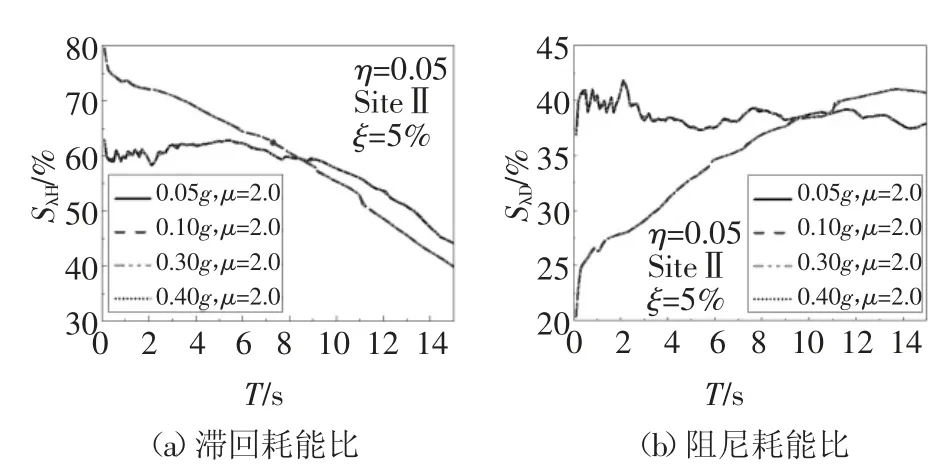
图19 PGA 对SλH 和SλD 的影响Fig.19 Effect of the PGA on the SλH and SλD

可见，若已知某基准PGAref下的SEI，ref，则其他PGAoth下的SEI，oth可根据PGAoth与PGAref比值的平方调整得到.

5 长周期地震输入能量设计谱

5.1 长周期地震弹性输入能量设计谱

以139 条长周期地震动记录作为输入，采用BISPEC 计算四类场地的长周期地震弹性输入能量谱的平均值NE1（见图20，PGAref=0.25g，对于长周期结构取ξ=2%），再采用三段式拟合函数[18，25]和最小二乘法对NE1进行拟合：

式中：NEI为的拟合值，即下文的长周期地震弹性输入能量设计谱；NEImax为NEI的平台段峰值；T1为峰值平台起始周期；Tg为峰值平台结束周期；r 为衰减指数；Δmin为最小误差.

在此基础上，可得四类场地NEI的拟合参数（见表3），并绘制NEI（见图20），而其他PGA 下的NEI可根据4.3 节结论，由PGAoth与PGAref比值的平方调整得到.

表1 NEI 的拟合参数Tab.1 Fitted parameters of NEI

图20 长周期地震弹性输入能量设计谱Fig.20 Elastic long-period input energy design spectra

5.2 长周期地震非弹性输入能量设计谱

5.2.1 μ 和ξ 对非弹性输入能量谱形状的影响

以Ⅱ类场地为例，将40 条长周期地震动记录的PGA 调幅为0.25g，采用Takeda 模型，并取η=0.05、ξ=2%，用BISPEC 计算μ=1.0～6.0 的非弹性输入能量谱（SEI，ξ=2%，μ）和弹性输入能量谱（SEI，ξ=2%，μ=1）的比值R1（见图21），对其拟合后得：

图21 μ 对R1 的影响Fig.21 Effect of μ on R1

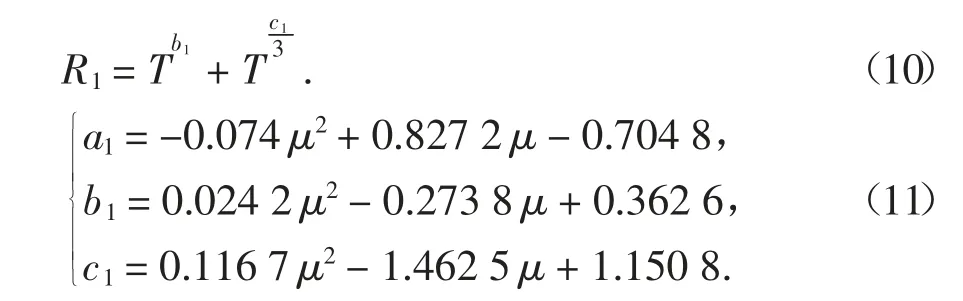
以Ⅱ类场地为例，将40 条长周期地震动记录的PGA 调幅为0.25g，采用Takeda 模型，取η=0.05、μ=4.0，再用BISPEC 计算不同ξ 的非弹性输入能量谱（SEI，ξ，μ=4）和ξ=2%的非弹性输入能量谱（SEI，ξ=2%，μ=4）的比值R2（图22），对其拟合后得：

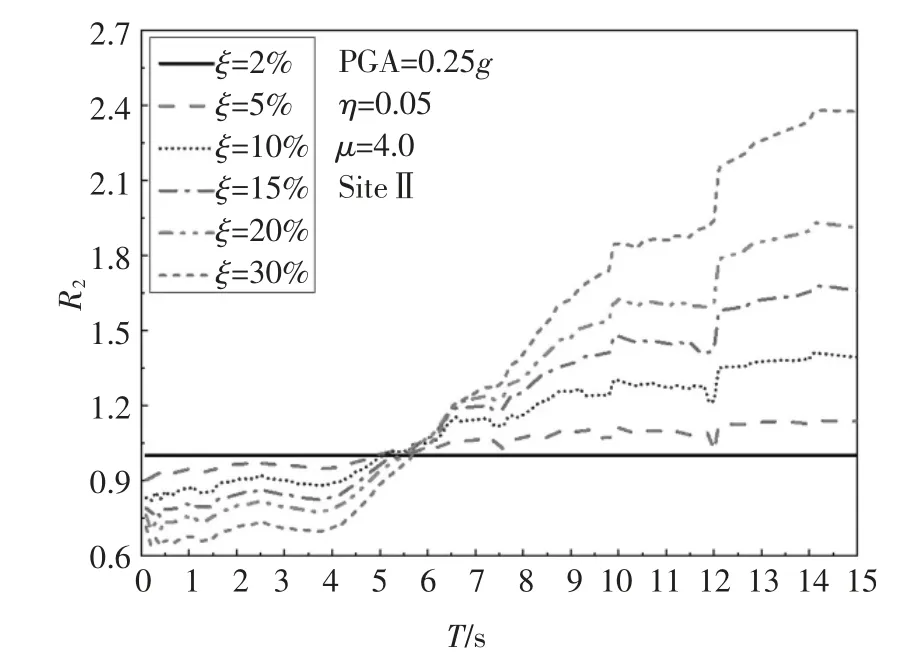
图22 ξ 对R2 的影响Fig.22 Effect of ξ on R2

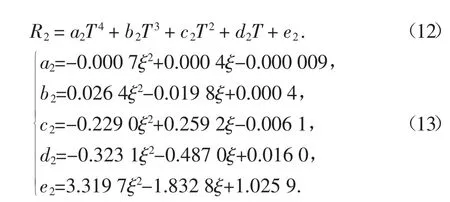
同理，其他三类场地的R1和R2拟合公式也可用上述方法获得.可见，具有不同μ 和ξ 的长周期地震非弹性输入能量谱（SEI，ξ，μ）与ξ=2%的长周期地震弹性输入能量谱（SEI，ξ=2%，μ=1）之比KT，ξ，μ为：

5.2.2 μ 和ξ 对非弹性输入能量谱峰值的影响

以Ⅱ类场地为例，将40 条长周期地震动记录的PGA 调幅为0.25g，采用Takeda 模型，取η=0.05，并用BISPEC 计算对应不同ξ 和μ 的非弹性输入能量谱峰值（SEImax，ξ，μ）和ξ=2%的弹性输入能量谱峰值（SEImax，ξ=2%，μ=1）的比值β.图23 为β 的均值加1 倍方差的结果，对其拟合后得：

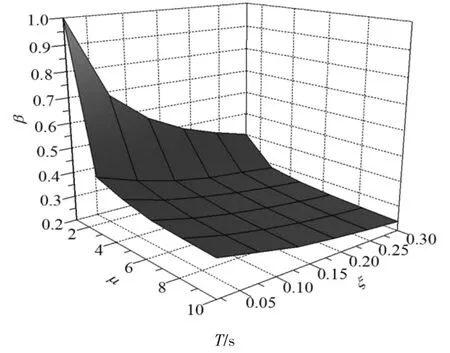
图23 μ 和ξ 对β 的影响Fig.23 Effect of μ and ξ on β

同理，其他三类场地的β 拟合公式也可用上述方法获得.

5.2.3 建立长周期地震非弹性输入能量设计谱

对5.1 节建立的长周期地震弹性输入能量设计谱（图20 的NEI）进行调整，以建立长周期地震非弹性输入能量设计谱（PEI）.步骤如下：

1）将NEImax乘以β，可得PEI的平台峰值PEImax，即PEImax=NEImax×β；

2）将Tg代入式（14）可得KTg，ξ，μ，再定义谱值调整系数γ（式（16）），将NEI的T >Tg段的谱值乘以γ后，可得到PEI的T>Tg段的谱值.

3）其他PGAoth下的NEI可根据4.3 节结论，由PGAoth与PGAref比值的平方调整得到.

在此基础上，以PGA=0.15g、ξ=2%、μ=4.0 为例，绘出四类场地的长周期地震非弹性输入能量设计谱PEI，如图24 所示.

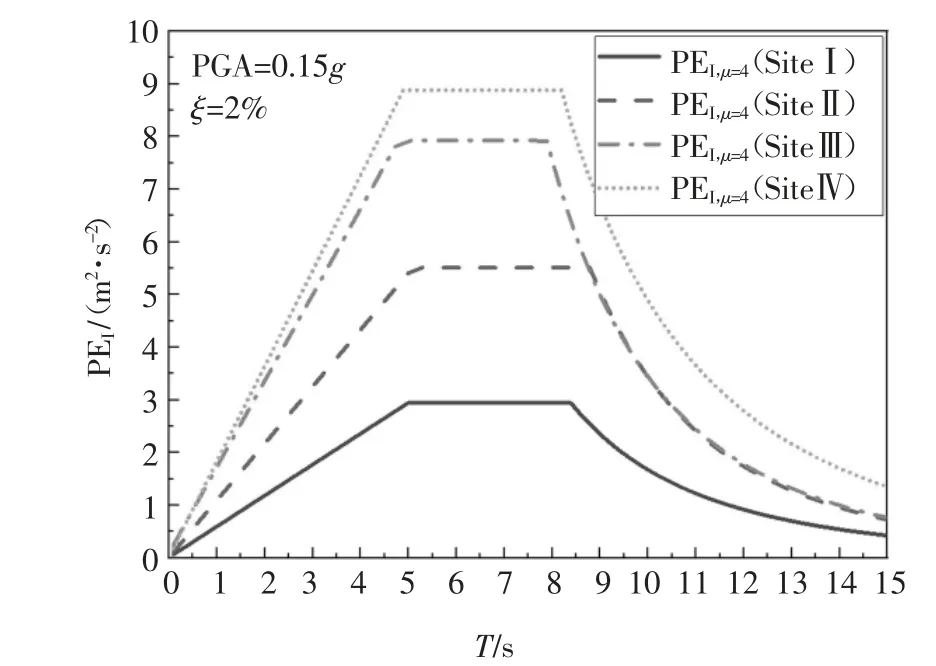
图24 长周期地震非弹性输入能量设计谱Fig.24 Inelastic long-period input energy design spectra

6 结论

选取了139 条长周期地震动记录作为输入，研究了恢复力模型动力参数和地震动特性对长周期地震能量反应谱的影响，得到以下结论：

1）相比刚度退化模型，无刚度退化模型能量谱的峰值平台、特征周期和中长周期段谱值都要长或大；可以忽略η 对长周期地震能量反应谱的影响；ξ对SEI有削峰作用，会增大SEI长周期段谱值，但不改变SEI峰值平台长度和特征周期；μ 对SEI和SED有削峰作用，会减小SEI和SEH的特征周期；随着T 或μ 的增大，各种因素对塑性铰滞回耗能能力和系统阻尼耗能能力的影响减小.

2）与常规地震能量谱的研究结果对比可知：恢复力模型对常规地震能量谱的影响随着μ 的增大而减小，但恢复力模型对长周期地震能量谱的影响则十分显著；无论是何种类型的地震动，η 对地震能量谱的影响都可以忽略；ξ 对常规地震和长周期地震的SEH和SED影响相同，但是，随着ξ 增大，常规地震的SEI的长周期段谱值减小，而长周期地震的SEI的长周期段谱值则增大；μ 对常规地震和长周期地震的SEI和SED的影响相同，但是，随着μ 增加，常规地震的SEH的峰值平台段后移（往原点方向）、平台段缩短、峰值增大，而长周期地震的SEH的峰值平台段后移、平台段延长、峰值降低.

3）MW越大，结构损伤也越大，使得塑性铰滞回耗能能力下降；场地越软，长周期地震能量谱值越大，塑性铰滞回耗能能力降低，而系统阻尼耗能能力则提高；若已知某基准PGAref下的能量谱，其他PGAoth下的能量谱可根据PGAoth与PGAref比值的平方调整得到.

在此基础上，采用三段式拟合函数，建立了长周期地震弹性输入能量设计谱NEI，并拟合了μ 和ξ 对长周期地震能量谱的影响公式，进而通过调整NEI谱值，以得到长周期地震非弹性输入能量设计谱PEI，可为长周期结构（如超高层建筑、大跨度桥梁）基于能量的抗震设计提供谱依据.