基于软件定义网络的卫星网络路由预置方法

孙延涛，刘承昕，李 琪，宁金枝

(1.北京交通大学 a.计算机与信息技术学院，b.交通数据分析与挖掘北京重点实验室，北京 100044；2.航天东方红卫星有限公司，北京 100094)

卫星通信在军事上有着其他通信方式不可替代的作用，目前，世界主要航天国家正在开展天基信息网的研究，着眼于提高军队的信息战能力，凭借这种夺取信息优势的关键武器在未来战争中获得主控权.我国的空间信息化建设正处于快速发展阶段，对大规模卫星通信有强烈需求.卫星组网和卫星路由的研究对于加强我国国防信息化建设，打好以夺取信息优势为目标的陆、海、空、天、电一体化战争具有重要作用和重大意义[1-2].

卫星根据其轨道高度可以分为地球同步轨道(Geosynchronous Earth Orbit，GEO)卫星和非地球同步轨道卫星两类.其中地球同步轨道卫星已广泛应用，但由于其轨道位置有限，资源日渐匮乏.而非地球同步轨道卫星的近地轨道(Low Earth Orbit，LEO)卫星有着传输延迟低、覆盖范围广、通信损耗小的特点，慢慢成为世界各国研究的热点.

卫星通信借鉴了地面的技术衍生出了星上处理技术和星间链路技术，使得卫星网络能像地面网络一样进行通信[3]，然而却也面临很多的问题.由于卫星网络特有的卫星节点负载有限、卫星网络拓扑变化频繁、软硬件设备更新困难、通信距离长等问题，常见的地面动态路由算法在卫星网络的环境中适应性很差，信息交换不及时导致的路由环路等问题造成网络丢包严重，网络吞吐量下降，传输延迟增加.为了解决上述问题，研究人员开始研究将软件定义网络技术应用于卫星通信网络[4].

软件定义网络(Software-Defined Network，SDN)是一种新型的网络架构，它将数据平面和控制平面分离，数据平面的节点只需要根据流表规则进行数据包的转发，计算则由控制平面的控制器完成[5].

本文作者利用卫星网络运行的规律性，提出了一种基于软件定义网络的卫星网络路由预置方法.在该方法中，SDN控制器提前获知网络拓扑情况，计算路由路径，然后下发流表条目.卫星节点根据收到的流表条目转发数据包，最终使得所有数据包能被转发到地面站.这种方法不仅保证了网络的正确运行，提高了吞吐量，降低了传输延迟，同时也减少了卫星上的路由计算开销.

1 相关工作

卫星组网路由方法一般使用动态路由算法及其变种.文献[6]提出基于优先级的自适应路由算法，该算法利用链路利用率和缓冲信息大小定义优先级函数，最终选取链路流量小的路径作为最优路径.文献[7]提出分布式多路径路由算法，该算法将业务流量分配到多条可行的路由路径上，达到单源多路径效果.但是这些算法实现复杂且在卫星网络环境下适应性差.

鉴于星间通信具有移动自组织网络(Mobile Ad Hoc Networks，MANET)[8]的一些特性，部分研究使用MANET的路由协议进行卫星通信.主要使用的是先验性路由协议中的链路状态路由协议(Optimized Link State Routing，OLSR)[9].但是OLSR需要不断在卫星之间交互邻居表等信息，在大规模星群的环境下会占用大量网络资源、增加端到端时延；且长距离通信环境下，消息交换不及时会导致路由环路等问题.

现有一些研究将软件定义网络技术应用于卫星网络.已经有不少研究提出了基于SDN的路由框架，文献[10]将地面站和地球同步卫星作为控制器，将近地轨道卫星作为数据平面节点，但是并没有实验验证.文献[11]在此基础上进行了实验的验证，但是卫星网络规模较小，仅由66颗近地轨道卫星构成，对于大规模星群并没有阐述其可行性.

对于卫星拓扑的路由问题，文献[12]提出了基于变形虫算法设计路由方案以及基于波纹扩散算法设计路由方案.文献[13]则结合了深度优先搜索和Dijkstra算法进行路由计算.但是这些方法相对复杂且并没有充分利用卫星运动的特点和软件定义网络的优势.

针对控制器放置问题，文献[14]提出了在近地轨道卫星网络中，间隔卫星部署控制器的方式.文献[15]提出了根据用户活动来动态部署控制器的方法，将控制器部署在活动强度较高的位置.文献[16]将主控制器设置在地球同步卫星上，并同时在近地轨道卫星上选取一部分卫星作为从控制器，完成对近地轨道卫星全网的控制.文献[17]结合了卫星网络和地面网络，提出了一种控制器和网关联合部署的策略.这些方法都试图控制器部署在卫星上，而并没有考虑卫星的处理能力缺乏一定的实用性.

总体而言，现有对软件定义卫星网络的研究并没有很好地解决大规模卫星网络的组网路由问题.

2 整体架构

本文将SDN应用于卫星网络中，根据卫星运动轨迹对卫星节点的路由进行预先设置，从而避免由于卫星网络拓扑变化频繁引起的路由震荡和丢包严重、通信延迟增加等网络性能问题.

本文所研究的卫星网络由地面站和LEO卫星组成，是一个以地面站为核心的网络.其中，LEO卫星负责采集气象等业务信息和卫星自身数据，定时发送给地面站，地面站负责信息数据的汇总与处理.为了达到更好的覆盖收集效果，星群使用双层甚至多层的卫星轨道.同轨道的卫星，其相对位置固定，使用激光与相邻的卫星进行通信；异轨道的卫星使用全向天线在一定的通信距离内与临近卫星进行通信.

该卫星网络具有一般卫星网络的特点：运行轨迹固定、通信距离长、路由跳数多.在该网络中，地面站是每个卫星的通信终点，每个卫星利用其他卫星作为中继节点，把采集到的数据最终发送至地面站.

针对上述卫星网络，本文采用的SDN卫星网络架构如图1所示.

图1 基于SDN的卫星网络架构Fig.1 Satellite network architecture based on SDN

1)SDN控制器.SDN控制器设置于地面，负责为每一颗卫星提前计算到达地面站的路由路径，并将计算结果预先下发到相应的LEO卫星.

2)数据平面.由LEO卫星组成，接收控制器下发流表项，并按照流表项对数据流进行转发.LEO卫星不需要进行路由计算，大大减少了星上计算负担.

3)带外控制信道.本文使用GEO卫星作为带外信道，用于Openflow控制平面和数据平面之间的控制消息交互.控制器通过带外信道将流表条目等控制消息发送给数据平面的卫星节点.相比于带内方式，使用带外方式交互控制消息，控制信道更为简单，通信时延更小.

3 路由预置方法

本文中使用的一些符号及其含义如表1所示.

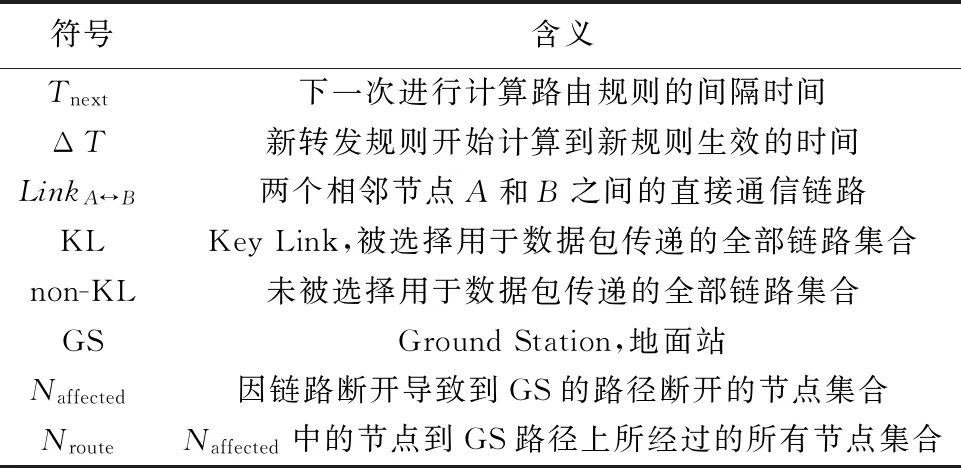
表1 文中的符号及含义Tab.1 Symbols and meanings in this paper

3.1 基本思想

在卫星网络中，卫星数量多且拓扑变化频繁，使用动态路由算法很可能会出现信息更新不及时造成的路由环路等问题，影响卫星网络的正常运行.引入SDN的思想虽然有助于解决错误的路由，但是由于卫星节点(后文简称节点)快速运动且和控制器之间距离较远，节点上报拓扑变化、控制器响应计算和重新下发流表条目这3个步骤都需要一定的时间，造成较大的延迟.

针对上述问题，本文提出一种基于SDN的路由预先设置的方法，预先根据网络拓扑变化计算路由，并提前将流表条目下发到相应的节点上.该方法的主要模块构成和工作流程如图2所示.

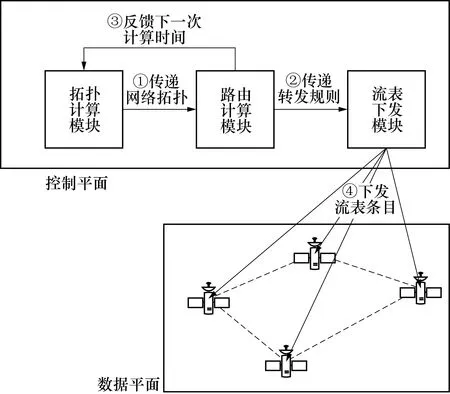
图2 路由预置方法模块组成与工作流程Fig.2 Module composition and workflow of route presetting method

本方法SDN网络的控制平面主要由拓扑计算模块、路由计算模块和流表下发模块组成.拓扑计算模块通过模拟获得网络拓扑；路由计算模块进行转发规则的计算；流表下发模块负责将转发规则下发.

工作流程分为4个步骤：

①拓扑计算模块收到反馈的Tnext后开启计时，到时间后通过模拟卫星的运动，得到ΔT后网络的拓扑情况，并发送给路由计算模块；

②路由计算模块收到拓扑后，计算新的转发规则，将结果交给流表下发模块；

③路由计算模块计算下一次的计算时间Tnext并反馈给拓扑计算模块；

④流表下发模块将收到的转发规则以流表条目的形式下发给对应的节点.

经过上述步骤后，数据平面上的节点最终根据收到的流表条目进行数据报文的转发.

3.2 路由计算模块

3.2.1 计算链路生存时间

卫星网络虽然是一个无线网络，但是不同于地面无线网络的是，每个卫星的运动是规律的、可预知的.例如，可以预先知道每个卫星的运动轨迹以及在其通信范围内的卫星.

基于上述特点，本文提出链路生存时间的概念.由于节点不断运动，网络中相邻节点之间的一条链路持续一段时间后会因为节点间距离不断增加而断开，这段持续时间称为该条链路的链路生存时间.具体定义如下：

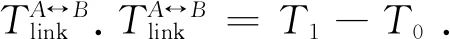
链路生存时间需要根据卫星的三维坐标进行矢量计算.根据节点A和B的运动轨道的方程式和位置随时间的变化计算节点间的距离，得到距离小于最大通信距离的时间范围.从而计算出LinkA↔B的链路生存时间.

每次运行路由算法前，需要完成对网络中每条链路的链路生存时间的计算，在路由算法中使用.完成路由计算后，路由计算模块需要计算出Tnext并反馈给拓扑计算模块.显然，下一次计算需要在任意链路LinkA↔B∈KL断开之前完成，结合链路生存时间的定义，Tnext的计算式如下

(1)

3.2.2 计算最短路径

在本文研究的卫星网络中，节点产生的所有的数据均是发往GS的，数据流的路由路径会形成一个以GS为根的树状结构.根据这一特点，路由计算模块使用Dijkstra算法计算每个节点到GS的最短路径.Dijkstra算法是经典的单源最短路径算法，被广泛应用于最短路径的路由计算中.

基于以上原因，将Dijkstra算法中的链路代价设置为链路生存时间的倒数，利用Dijkstra算法计算出以地面站为根的最短路径树.

在完成每个节点的路径计算后，还需要计算路径的持续时间，其目的一是流表下发模块需要确定流规则的有效时间，二是为了更简单地确定Tnext并反馈给拓扑计算模块.为此，本文中提出了节点路径持续时间的概念，定义如下：

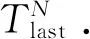
路径持续时间的计算则利用树的递归特性，计算公式如下(假设B到GS的下一跳为A)：

(2)

计算出路径持续时间后，Tnext的计算可以简化为(网络拓扑图表示为G=)

(3)

3.2.3 新旧最短路径树的合并

3.2.2节为每个节点计算了新的最短路径树，但是考虑到此时卫星网络中正在使用上次计算下发的旧路径树，而需要新的最短路径的节点仅为受断开的链路影响的节点集Naffected，其他节点仍可使用旧的最短路径进行转发.直接将路由算法的结果下发的方式效率很低，且控制开销较大.

针对上述情况，本文提出了一种将新旧最短路径树合并的算法，如图3所示.

图3 链路断开时的处理结果Fig.3 Processing results when the link is down

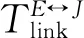
(4)

找到受影响节点后，在Tpre+Tnext时刻新一次路由计算得到图3(b)的计算最短路径树,之后根据新计算的路由规则，找到Naffected中的节点到GS路径上所经过的所有节点，其集合为Nroute.

进行路径树合并时，只需要修改Naffected和Nroute中的节点转发规则，其他节点不需要修改,得到图3(c)的新最短路径树.详细算法如下

算法1：最短路径树合并算法

输入：Tnext, 拓扑图G，持续时间集合Tlast，下一跳集合nextHop

输出：新的Tlast，nextHop

1. Naffected = {Ni，Tlast[Ni] == Tnext }

2. status = {};

3. for 0 ≤ i< n do

4. Tlast[i] = Tlast[i] - Tnext

5. if i ∈Naffected then

6. status[i] = 1;

7. else

8. status[i] = 0;

9. end if;

10. end for;

11. Dijkstra算法根据G得到集合next_comp, T_compute;

12. for Ni ∈Naffected do

13. tmp = next_comp[Ni];

14. nextHop[Ni] = next_comp[Ni];

15. Tlast[Ni] = T_compute[Ni];

16. whiletmp != Dst and status[tmp] == 0 do

17. nextHop[tmp] = next_comp[tmp];

18. Tlast[tmp] = T_compute[tmp];

19. status[tmp] = 1; tmp = next_comp[tmp];

20. end while

21. end for

22. 输出Tlast, nextHop

算法中第11行对应图3中的“计算的最短路径树”，next_comp和T_compute分别对应由路由算法得到的下一跳集合和路径持续时间集合.第1行到第10行确定所有的Naffected并且在第3行开始的循环中利用集合status对其进行标识.第12行到第21行主要进行最短路径树的合并，其中第16行开始的循环通过下一跳集合确定Nroute，最终得到新最短路径树.

上述合并算法可以在变动最少的情况下，保证更新节点的路径最优、其他节点的路径不差于旧规则.分3种情况讨论：①对于Naffected和Nroute中的节点(图3中白色节点I、J、K以及灰色节点B、D、E、F、G)，其转发路径是根据最新拓扑使用Dijkstra算法计算的最佳路径.②对于其他节点，若其路径上没有灰色节点(图3中黑色节点A、C)，则转发规则为旧的最短路径.③若其经过灰色节点(图3中的黑色节点H)，由于GS到G的路径符合情况1，G到H的路径符合情况2，所以H的路径优于旧路径.

综上，最短路径树合并算法既确保了全网节点的转发效率；同时也减少了需要修改的节点的数量.

3.2.4 设置观测时间

虽然合并算法减少了控制平面和数据平面之间控制消息的数量，但是带来了一个问题.很多时候会出现几条属于KL的链路，它们链路生存时间相近，就需要在断开的时候分别进行计算.如果能将这几次时间相近的计算同时完成，将可以大大减少控制平面的计算量.

为了解决上述问题，设置观测时间Tinterval，然后将所有的链路生存时间全部统一为Tinterval的倍数，不到Tinterval的则删除，再进行节点路由路径的计算，如图4所示,其中Tinterval=100 s.

(a)指示链路生存时间的网络拓扑图(单位:s)(b)指示观测时间倍数的网络拓扑图(单位:Tinterval)

图4利用观测时间统一链路生存时间

Fig.4 Unifying link lifetime using observation time

将所有时间统一为倍数之后，在每次计算完成过后，至少会经过Tinterval的时间才会需要进行下一次的计算，不会出现很短时间后就需要再次计算的情况.

最后是Tinterval的取值问题，如果太大，会消除掉过多的链路，增加到终点的跳数；如果太小则会削弱Tinterval的作用.因此需要在这之间做折中，根据实验确定.

3.3 流表下发模块

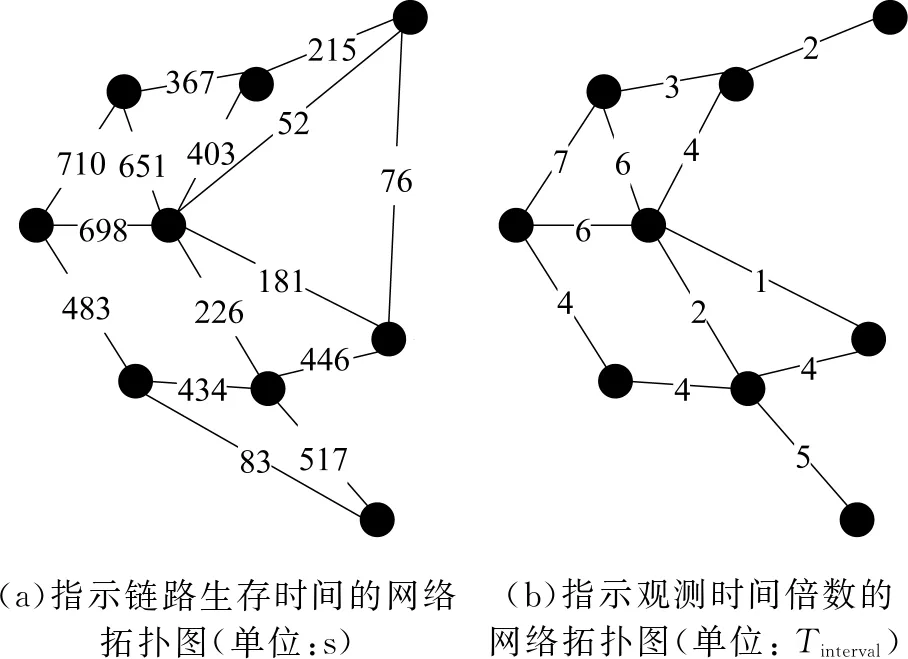
路由预先设置的另一个问题是每个节点中流表的同步生效问题.如果更新的节点出现部分使用旧规则，部分使用新规则的情况很容易导致路由环路.因此如何保证所有新规则同步生效决定了卫星网络的传输效率.工作流程如图5所示.

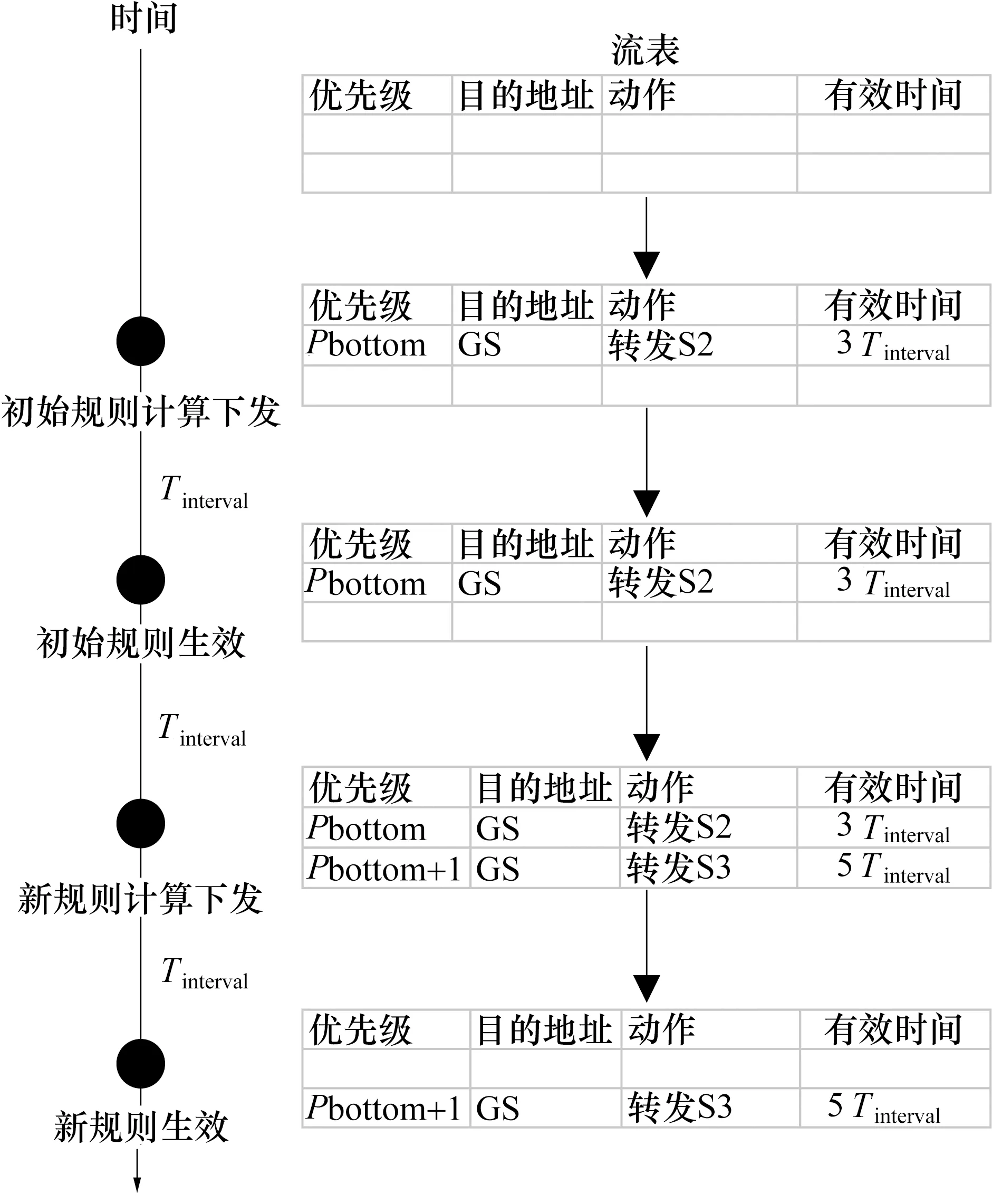
图5 流表修改过程Fig.5 Flow table modification process

为了使得不同节点中的规则能够同时生效，本文将Openflow协议流表项中的优先级(priority)和有效时间(hard_timeout)结合使用.优先级需要先为每个节点定义一个优先级pN，同时定义一个范围Pbottom到Ptop作为路由预置的使用范围.有效时间则为节点的路径持续时间加上从计算到生效所需要的时间ΔT，这里利用观测时间Tinterval，规定路由路径的计算在生效前Tinterval进行，这样ΔT=Tinterval.整个过程分为

1)将每个节点的优先级pN初始化为Pbottom；

经过以上过程，新下发流规则后，节点的流表中会有优先级高的旧规则，和优先级低的新规则，在旧规则到期被移除后新规则就会自动接力，实现每个节点之间的同步更新.

4 仿真结果及分析

实验使用RYU 4.34控制器和Riverbed Modeler 18.6仿真软件联合完成，对提出的路由预置方法进行验证.目前Riverbed中的SDN交换机模型仅支持地面上的有线通信，本文对该交换机进行修改，增加了无线通信功能，并支持根据导入的卫星轨道进行运动.搭建大规模星群仿真场景，使用Riverbed中的SITL接口连通仿真环境和外部RYU控制器.实验中设计多个场景评估本文提出的路由预置方法的性能.由于常见的动态路由协议中，OLSR路由协议发挥了MANET的特性，在卫星网络中的表现更好，因此将实验结果与OLSR路由协议进行对比.

4.1 仿真参数设定

本文设计了60、120和180个节点3个不同规模的仿真实验场景，全网所有节点发送的业务总量大小从1.1～1.5 Mbps.双层卫星轨道，高度分别为500和700 km.地面站设置在西安.参数设置如下：仿真时间为3 600 s；同轨道面通信距离为4 500 km，异轨道面为1 200 km；同轨道面链路速率为1 Gbps，异轨道面为8 Mbps.

4.2 算法性能

本文的路由预置方法在控制器端的运行时间如表2所示.

表2 算法执行时间Tab.2 Algorithm execution time

表2结果显示本文方法可以在5～10 ms内完成对所有节点路由路径的计算，几乎不会对从计算到生效所需的时间ΔT产生影响，因此不会影响流规则中hard_timeout的准确性.

表3展示了180个节点场景中不同观测时间下采用新旧最短路径树合并的方法和直接下发新规则的方法，在下发的流表条目数量上作对比，其中Tinterval=1 s可以视为没有设置观测时间.可以看到采用合并的方法可以使控制器下发的流表条目数量降低50%以上，大大减少了网络中控制消息的数量，减轻带外信道通信链路的负担.

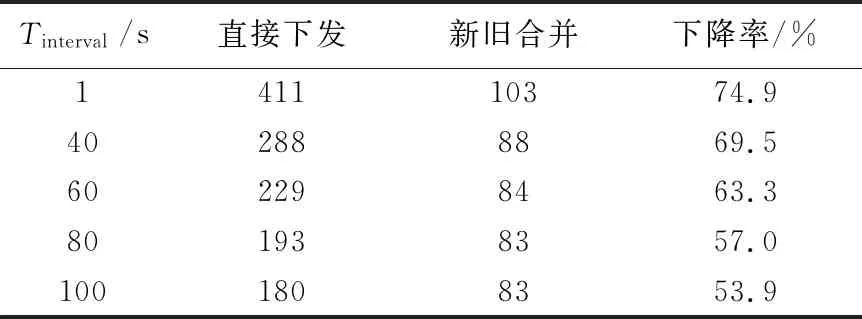
表3 每100 s下发的流表条目数量Tab.3 Numbers of stream per 100 s table entries distributed

另外，随着Tinterval的增大，流表条目数量在逐渐减少，这是因为设置了Tinterval后，合并了时间相近的计算，减少了路由计算的次数.从Tinterval=60 s开始，流表项数量的减少开始进入瓶颈，变化趋于平稳.

表4展示了全网节点到地面站的最短路径的跳数和Tinterval的关系，其中跳数随着Tinterval增大而增大.这是设置Tinterval后，删除拓扑中的部分链路所带来的影响.结合前面对流表条目数量的讨论，本文后续的实验中，将Tinterval设置为60 s.

表4 全网节点到地面站的跳数Tab.4 Number of hops from the whole network node to the ground station

图6展示了Tinterval=1 s和Tinterval=60 s时，流表条目数量随节点数量的变化情况.可以看到直接下发方法和新旧合并方法的流表条目数量都和节点数量呈线性正比关系，因此前面对Tinterval取值的讨论可以适用于不同大小的网络规模.

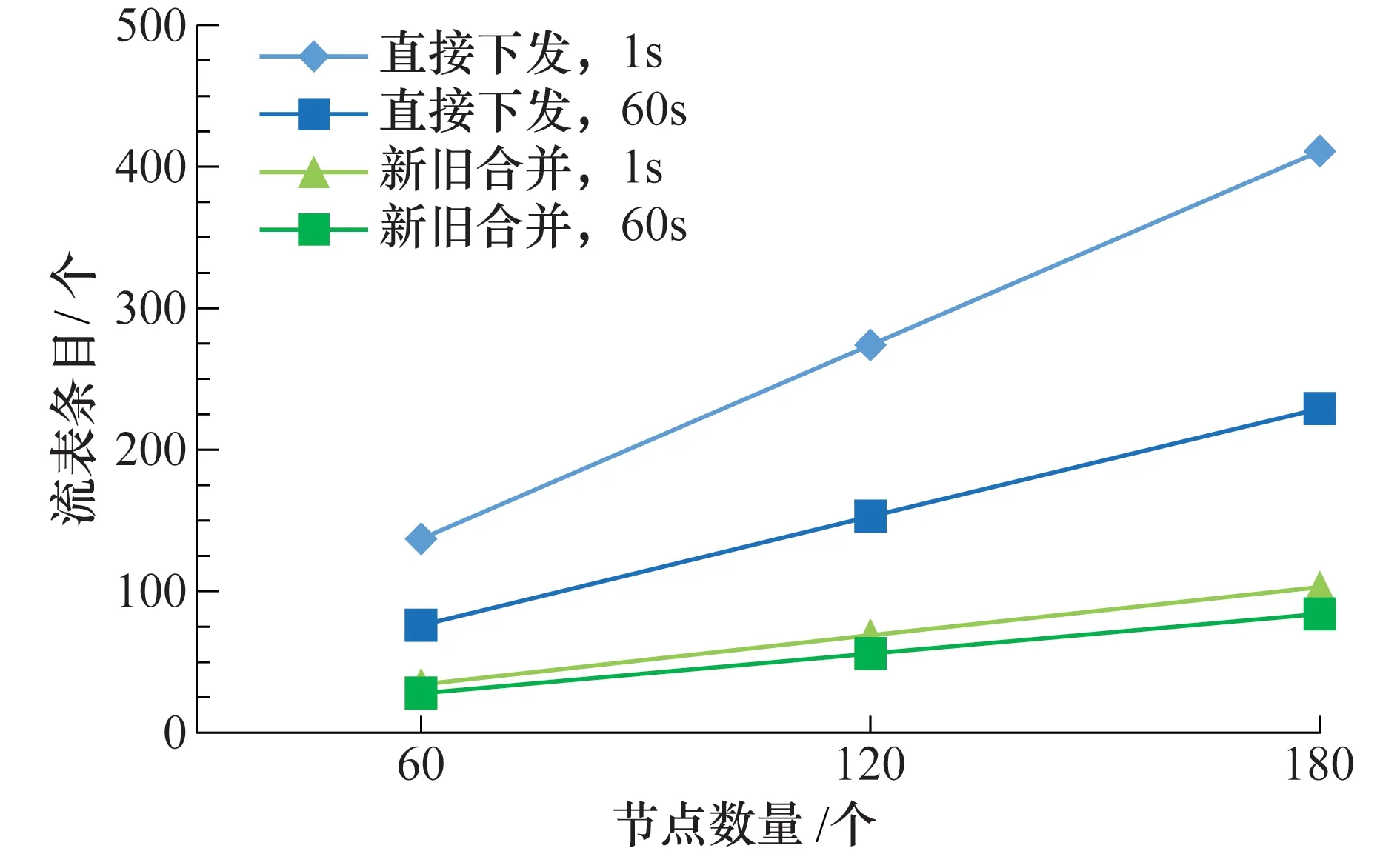
图6 节点数量和流表条目数量的关系Fig.6 Relationship between node number and flow table entry number

4.3 仿真结果

为了避免可能的随机性带来的影响，对比实验的数据均为运行10次的平均值，3种不同规模实验场景的数据为不同业务量大小下的平均值.

图7展示了3种场景大小下，路由预置方法和OLSR的端到端时延的变化趋势；图8则为180节点场景下时延随业务量大小的变化.可以看到OLSR的时延随业务量和网络规模变化明显，而路由预置方法则非常平稳，都在100 ms左右.这是因为OLSR的控制开销会占用通信链路的带宽，增加队列阻塞的概率，且动态路由算法的结果并非最优；而本文的方法使用带外信道的方式传输控制命令，不会对通信链路的带宽造成影响，且使用Dijkstra算法计算路径，是当前拓扑下的最优解.

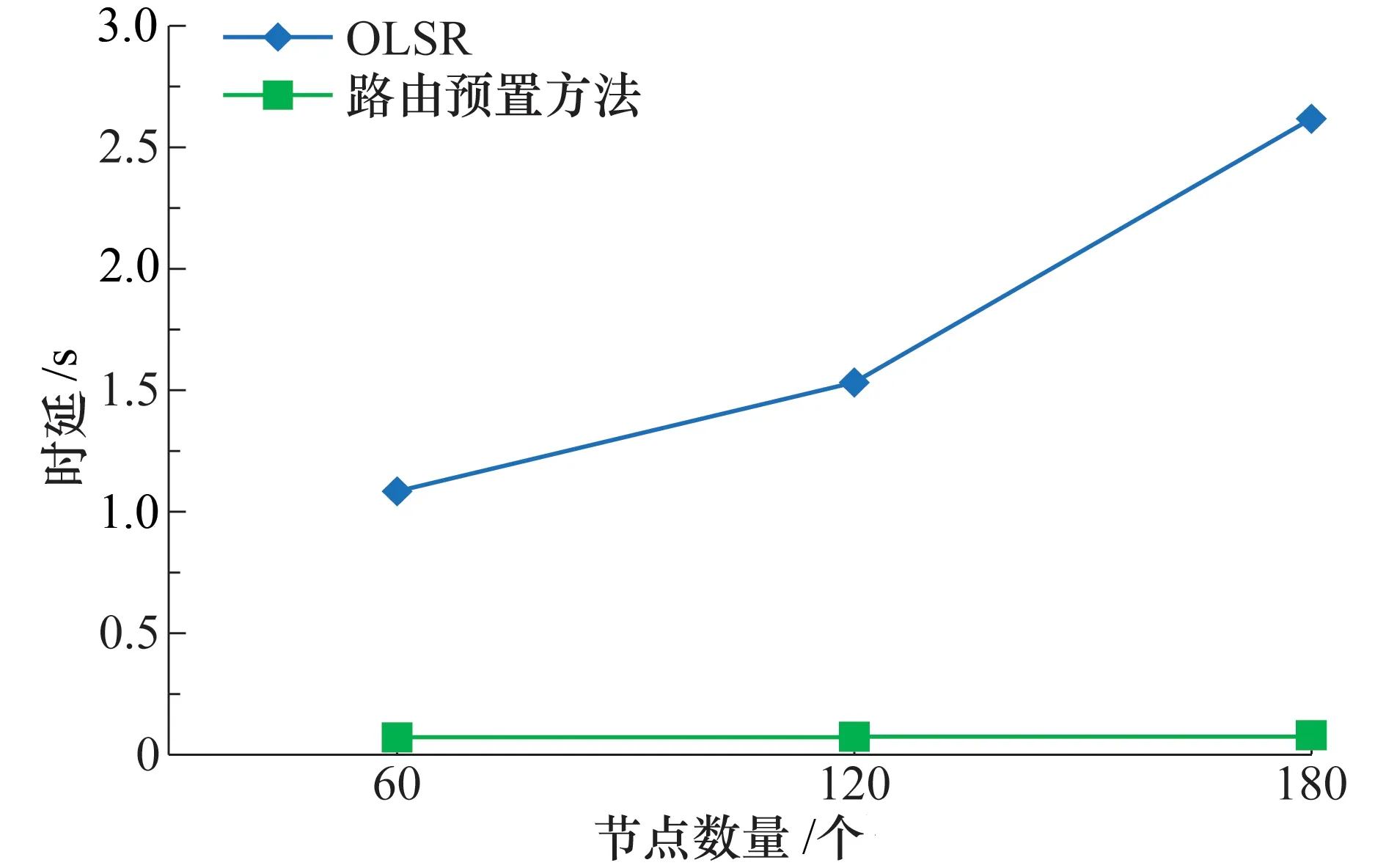
图7 网络节点数量和时延的关系Fig.7 Relationship between the number of network nodes and delay

图8 业务发送量和时延的关系Fig. 8 Relationship between service transmission volume and delay

两种方法在3种场景大小下，丢包率的变化趋势如图9所示.由于OLSR的控制开销和节点数量呈正比，节点数量增加后，控制开销的数量也迅速增加，极大地占用了通信链路的资源，导致OLSR的丢包率随节点数量的增加大幅上升.而路由预置方法采用集中式的控制方法，对节点数量的变化不敏感，因此相对平稳，丢包率仅为0.3%.

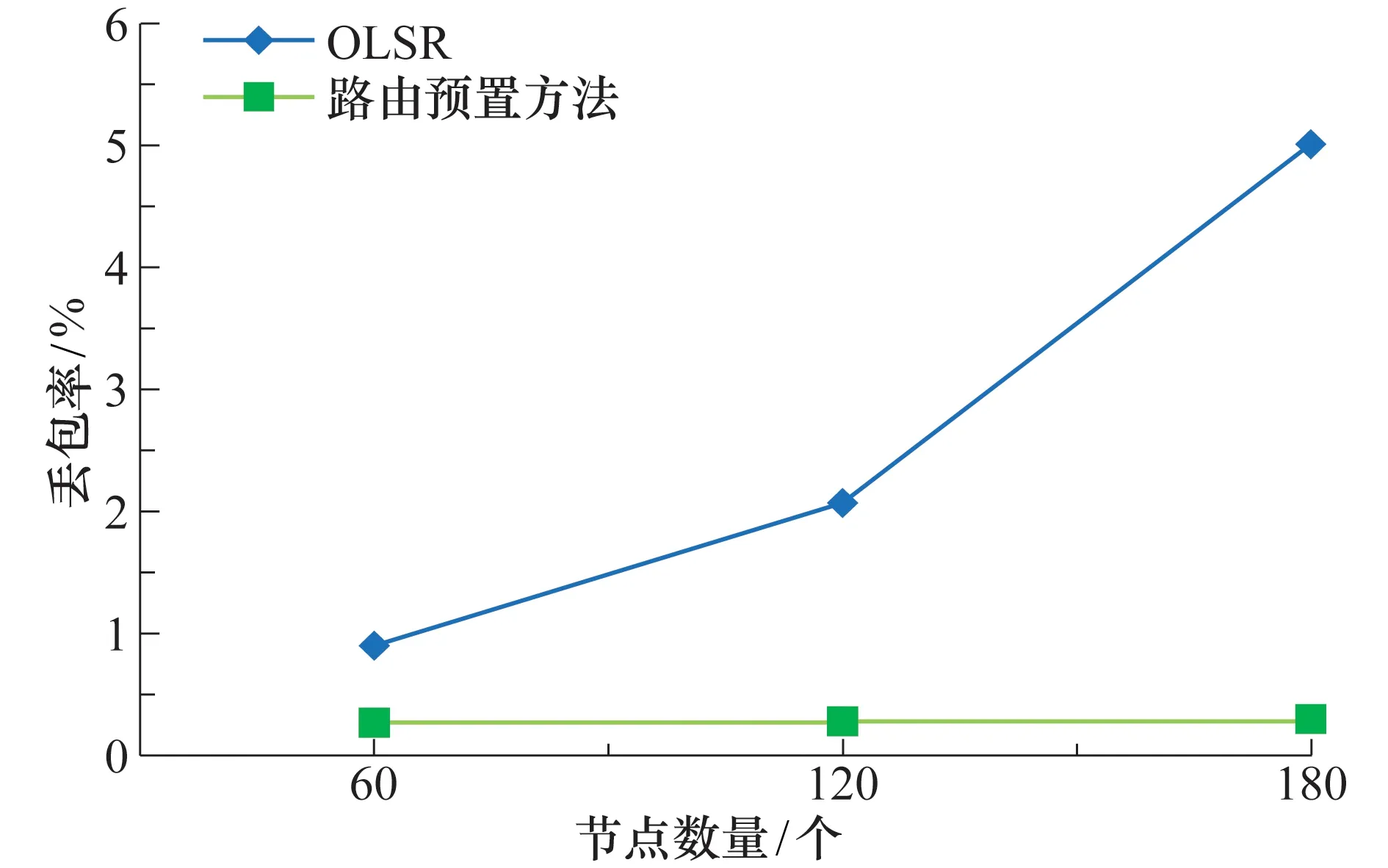
图9 网络节点数量和丢包率的关系Fig. 9 Relationship between the number of network nodes and packet loss rate

路由预置方法和OLSR路由协议都需要一定的控制开销，但是考虑到OLSR的控制开销占用通信链路，而路由预置方法使用的是带外信道，因此本文不对二者的控制开销进行对比.

5 结论

1)提出了一种卫星网络的路由预置方法，基于软件定义网络的思想提出了相应的网络架构，并提出了路由计算和流表下发的策略.本文方法与OLSR方法进行对比，在多种网络规模和不同业务大小的场景下比较了丢包率和端到端时延.

2)结果表明，本文的路由预置方法具有更低的时延和丢包率，在卫星网络下的表现更好.

本文中的路由方法仅考虑了链路的生存时间，而并未考虑链路的负载量等因素，因此下一步的工作将在本文基础上，结合软件定义网络的负载均衡做进一步的研究.