声发射检测信号分析及源定位方法研究
童国炜,周循道,黄林轶,陈超英,徐华伟,杨 林
(工业和信息化部电子第五研究所,智能产品质量评价与可靠性保障技术工业和信息化部重点实验室,广东广州 510610)
0 引言
声发射(acoustic emission,AE)是一种由于裂痕扩展、摩擦、微动、冲击而产生的物理现象,通过定位AE源可实时监测、评估裂痕和损伤的状态,能够达到预防和控制潜在危险及确保监控对象安全运行的功能。由于其具有快速、无损、低能耗等特点,现已广泛应用于地震、爆炸、航空、军事、桥梁、隧道、矿山和能源等领域[1-2]。
1912年,Geiger最先提出了一种基于地震波到达时间确定震源的方法[3]。受其启发,学术界涌现出了众多定位方法,并广泛地应用于工程领域中。针对现有AE源定位算法不能始终获得多层圆柱介质精确结果的问题,作者提出了一种考虑折射的AE源定位方法。实验结果表明,新方法可以在双层圆柱表面介质中获得准确的声发射源位置[4]。作者针对固定的弹性波速度和结构几何不规则性等问题,提出了一种没有预先测速的A*定位方法。实验结果表明对于不规则的二维复杂结构,其定位精度得到了显著提高[5]。上述方法推动了AE定位技术的发展,但是这些方法在设计时未考虑到在工程实际应用过程中存在的环境测量噪声,同时也未考虑在非理想、非均匀、非完全弹性介质中传播的波会发生的频散现象,上述问题均会降低定位算法的准确性、可靠性,或者导致定位到现实中不存在的源。研究表明,通过信号分解方法将原始AE源信号按频率特征进行分解,并选择性地选取用于计算定位信息信号的验算策略可有效地弱化噪声和频散现象的不利影响。变分模态分解(variational modal decomposition,VMD)方法[6]可通过非迭代的方式实现按最小估计带宽对信号的分解,借助信号能量分析方法可选择出用于计算定位信息的分量信号。因此,本文提出了一种融合了VMD方法和互相关分析方法的AE源定位算法。VMD方法将AE信号分解为若干个具有最小估计带宽的分量信号,能量分析方法挑选出信号的主要成分,互相关分析获得2个AE传感器之间的时间差,进而计算得出声源距离AE传感器的距离信息,实现了对声源准确、可靠的定位。
1 声发射及定位原理
1.1 声发射
如图1所示,AE系统包括3个部分:AE传感器、信号放大器和信号分析系统。AE系统在工作过程中,声源产生的瞬时弹性波以工程材料作为介质传播到材料表面,然后与材料表面放置的AE传感器进行耦合,通过压电效应将声波转换为电信号,最后经放大、采集可得到数字化信号,并采用适当的分析方法得到AE源的信息。
1.2 定位
当测量材料产生连续或间断的AE信号时,通过采集多个AE传感器中的信号,可分析出声发射源的位置及其他信息。图2以一维测量模型为例演示了定位算法。
一维模型一般存在2个或2个以上AE传感器[7],图2仅示意存在2个传感器的情况。设声发射源所产生的信号分别经过t1和t2时间达到传感器1和2,声音在材料中传播速度为v,可得如下关系:
(1)
式中:d为AE源到传感器1的距离,m;D为传感器1、传感器2的距离,m;Δt为AE源到达传感器1、传感器2的时间差,s。
当已知声波的传播速度v和Δt时,即可得到d,从而确定AE源的位置信息。本文采用Nielsen-Hsu实验确定值为3 446 m/s。
采用互相关分析估计时延Δt,该方法计算速度快、运行损耗小。假设两侧传感器采集的AE信号分别为x(t)和y(t),则对应的数学模型如下所示:
(2)
式中:s(t)为AE源的信号;a为衰减参数;n1(t),n2(t)为环境噪声。
在某一时间段T内,互相关系数为
(3)
观察式(3)可知,2个声发射信号是延迟时间Δt的函数,因此互相关系数分布的峰值点表示2个信号最大相关的位置,同时也代表了信号传播时差。
基于一维定位模型理论,二维定位模型通过布置于平面内3个或3个以上传感器所获取的信息对AE源进行定位[8]。当获得1对传感器信息后,可在平面内获得1条双曲线函数,如图3(a)所示。当获得2对传感器信息后,即可在平面内确定2个声源点,如图3(b)所示。
假设P点为声发射源,传播到传感器1和传感器2的时间差和距离有如下关系:
|PF1-PF2|=vΔt
(4)
当采集3个AE传感器的信号后,声发射源的位置会处于2条双曲线上的交叉点上。因此,需采集3个及3个以上AE传感器的信号才可以确定二维平面内声发射源的位置,如图3(b)所示,P1和P2为2条双曲线的交点,声发射源的位置在其中之一,选取时根据实际情况进行选择。
1.3 信号预处理
由于环境噪声和频散效应对声波的影响,直接使用采集到的原始AE信号计算互相关系数,并查找判断延迟时间,所获得的结果会存在一定偏差。因此,选择合适的方法对原始信号进行有效的筛选、分析、优化是提高定位精确性和可靠性的关键。在信号分析领域中,VMD是基于信号时频特征的分解方法,通过非迭代的方式将信号分解为若干个拥有不同带宽的模态函数(mode function,MF)。该方法认为每个MF分量有且只有一种频率成分构成,分解过程是寻求若干个MF,同时要保障每个MF所包含的带宽最小[6]。
对于序列x(t),VMD可分解出K个MFuk(t),k=1,2,…,K:
(5)
MFuk(t)定义为
uk(t)=Ak(t)cos[φk(t)]
(6)
式中:Ak(t)为uk(t)的幅值;φk(t)为uk(t)的相位。
对uk(t)使用Hilbert变换,可得解析信号及其单边谱:
(7)
通过指数调谐,即乘以e-jwkt,将估计uk(t)的中心频率移到基频附近:
(8)

带宽B[uk(t)]可通过解调信号的H1高斯平滑度进行估计:
(9)
最终,得到一个变分优化问题:
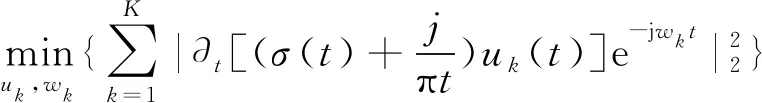
(10)
原始文献采用交替迭代乘子法进行求解。观察可知,VMD方法采用优化策略一次性获得所有分量,而且各MF的中心频率和带宽可被自适应计算出的同时,实现了对序列的频域剖析和MF分离。
2 实验研究
本文设计了AE定位测试系统,由3个AE传感器、3个前置放大器、1个8通道的数据采集卡、1个PC机,1个镀锌钢板组成。镀锌钢板长、宽为500 mm,厚度为2 mm,通过敲击产生AE源。实验模型如图4所示。镀锌钢板固定于桌面,3个AE传感器通过磁吸附的方法固定于镀锌钢板表面,AE传感器通过前置放大器与数据采集卡相连。
根据文献报道,敲击震动信号的峰值频率较低,因此,本文选用窄带低频的AE传感器采集声信号,相关参数列于表1。

表1 传感器参数表
设计了针对一维和二维定位模型的实验,每种实验情况的传感器摆放方式和敲击位置又设定了不同的组合,通过组合可得4种实验情况,图5展示了传感器和敲击位置的具体坐标,表2列举了4个测试案例。

表2 实验分类
3 实验结果分析
本小节分别对4个案例进行实验测量,并采用本文所提方法确定AE源位置,对其有效性、精确性、可靠性进行验证。
3.1 信号分析
以案例1为例,图6为AE传感器1、传感器2接收到的声信号,相应的VMD分解结果如图7所示。
在案例1中,原始信号被分为4个模态函数,在时域波形中,MF的幅值会逐渐减小,同时频带会升高。因此,具有较低信号幅值和较高频率的MF分量可以被认为是噪声干扰而忽略不计。同时,每个MF的能量EIMFi和相应的能量比RIMF由下式进行量化:
(11)
(12)
式中xi(m)为第i个MF中第m个时间序列点的数值。
图8显示了案例1中2个AE传感器接收到声信号MF的能量比。如图8所示,前3个MF几乎包含整个信号能量的98%,可以完全反映原始信号的主要信息。因此,MF1、MF2、MF3可用于重建AE信号的主要成分,而其他能量较低的成分可以忽略不计。
3.2 一维定位模型
合并2个AE传感器信号前3个MF,由式(3)计算2个信号的互相关系数,并从峰值处获得时间差,通过式(1)计算出声发射源的位置。案例1-2的相关系数曲线如图9所示,定位结果列于表3。
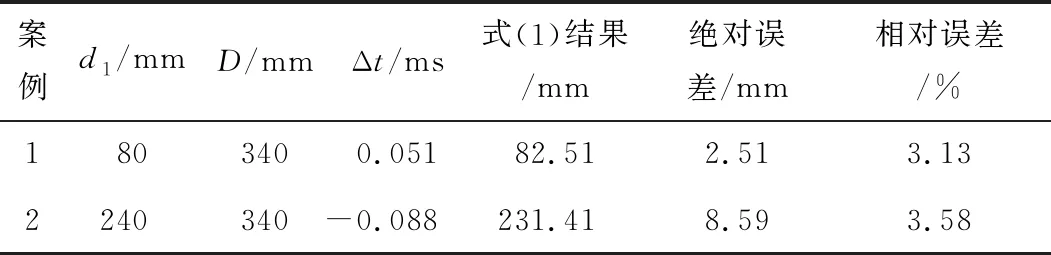
表3 一维模型声发射源定位结果
根据实验结果可知,本文设计的定位算法能够实现AE源的定位,且具有较高的定位精度,在案例1,2的实验中,相对误差可达到3.13%,3.58%,满足实际应用要求。
3.3 二维定位模型
基于一维定位模型的计算方法,采用2对AE传感器的数据,通过双曲线方法可实现二维平面内的AE源定位,结果如表4所示(坐标原点在图5的左下角)。通过2组二维平面AE源定位实验,可验证本文所提方法对二维平面AE源定位是有效的、精确的,实际计算结果的横纵坐标定位误差在5%以内。

表4 二维模型声发射源定位结果
4 结论
为了减小AE源定位过程中测量环境噪声和频散现象对定位结果的干扰,本文研究了VMD方法在AE源定位中的应用方法,通过对原始AE信号按最小带宽进行分解,提取主要能量分量的和,并采用互相关分析确定AE源位置。一维和二维AE源定位实验结果表明本文所提方法综合定位误差在5%以内,可实现精确的AE源定位计算,为AE源定位研究提供了一种可行的研究方法。

