白鹤滩水电站蓄水引起重力与库仑应力变化的模拟研究
佘雅文, 付广裕, 赵倩, 郭凌冬
1 中国地震局地震预测研究所(地震预测重点实验室), 北京 100036 2 南京大学地球科学与工程学院, 南京 210023
0 引言
白鹤滩水电站坐落于金沙江上,是一座位于云南省巧家县与四川省宁南县交界处的水电站.建成后将成为仅次于三峡水电站的中国第二大水电站,世界第三大水电站.水电站正常水位为海拔825 m,相应库容达到206亿m3.大型水电站由于其庞大的蓄水量势必会在库区和临近区域造成较大的重力和应力变化,研究蓄水过程的重力和库仑应力变化对于深入研究地表水储量变化、库区水渗透、负荷形变、地震触发等问题具有重要参考价值.
针对大型水电站蓄水引起的重力变化研究,不同学者利用地表和卫星等观测数据得到了一系列研究成果.Wang等(2002)基于三峡水电站蓄水数据,利用球体负荷理论获取了不同蓄水水位对应的重力变化,其研究结果表明,三峡库区蓄水在临近区域最大可产生约3.5 mGal的重力变化.孙少安等(2006)在三峡水电站2003年蓄水期间进行了多次重复重力观测,捕捉到库坝地区的重力变化约为0.2 mGal.汪汉胜等(2007)利用GRACE(Gravity Recovery and Climate Experiment)数据研究了三峡库区的水储量变化,认为GRACE可以监测该地区每个月的水储量变化.詹金刚和王勇(2011)利用GRACE数据研究了龙滩水电站蓄水引起的重力变化,认为GRACE观测到的2.17 μGal的重力信号阶跃是该水电站蓄水引起的.Wang等(2019)基于GRACE、GPS和实测水位等数据研究了三峡地区的水储量变化,认为GRACE数据在联合其他数据的情况下,可以探测到水库蓄水的信号.以上研究表明,大型水库蓄水引起的重力变化是可以被地表和卫星重力观测捕获的.
大型水库蓄水势必会造成地壳内部的应力变化,该过程与触发地震息息相关.据不完全统计,90多个国家发生过一定强度的水库诱发地震(Gupta, 2002).其中,1967 年印度戈伊纳水库初次蓄水就诱发了6.3级强震,是迄今全球最大的水库地震(Shashidhar et al., 2019);1962 年新丰江水库建成后,初次蓄水就在水坝下游1.1 km处触发了6.2级地震,为我国最大的水库地震(丁原章,1989).近年来不同学者利用库仑应力和孔隙压变化的时空分布结果研究了紫坪铺、新丰江和三峡等水库蓄水触发地震的可能性(雷兴林等, 2008; Ge et al., 2009; Deng et al, 2010; 程惠红等, 2012, 2015; Tao et al., 2015; Zhang et al., 2016),但是由于断层几何形态、震源深度、地壳物性参数等因素的不确定性,该问题尚无定论.白鹤滩库区历史地震反映了该地区地震活动背景较为强烈(图1),2014 年发生过鲁甸6.5 级地震,2020 年3 月距离水电站仅10 km的地方又发生了3.6 级地震.因此,即将开启的白鹤滩水电站蓄水过程是否会触发强震,是一个具有科学和社会价值的问题.
在白鹤滩水电站即将投入使用和开始蓄水的前期,本研究将对白鹤滩水电站蓄水引起的重力和库仑应力变化进行模拟计算研究.首先,基于重力和地形模型数据研究了该地区的背景重力异常场,并给出了均衡重力异常场.其次,利用地形数据模拟了不同水位的蓄水量,计算了不同水位蓄水引起重力变化的量级和分布情况,并基于该结果模拟研究了GRACE-FO可观测到的蓄水重力变化.该结果不仅对后续开展地表重力观测工作具有重要指导意义,同时也对水库蓄水后利用GRACE-FO数据进一步研究该地区的重力变化和水储量变化具有参考价值.最后,基于负荷理论计算了水电站蓄水引起的弹性应力变化,并给出了临近断层的库仑应力变化结果,进而讨论了这一过程触发地震的可能性.
1 数据
1.1 白鹤滩水电站模拟蓄水数据
为了细致的提取水库蓄水后的水体分布和三维形态,以便后续计算其引起的重力变化.本文使用的地形数据为Shuttle Radar Topography Mission(https:∥www2.jpl.nasa.gov/srtm/)提供的1″数据,空间分辨率大致为30 m×30 m.水库库区是不规则的三维水体区域,为了方便后续重力值计算,将水体分为多个等高的水层处理,再将水层分为等体积的单元水体.针对白鹤滩水库蓄水问题,将单元水体设定为56 m×56 m×10 m的立方体.白鹤滩水库蓄水正常水位为海拔825 m,对应的库区范围如图1所示.鉴于此,本研究将模拟水位分别设定为700 m、750 m、800 m和825 m,对应的单元水体数量为67569、205169、427723和543685.利用以上数据即可计算不同水位蓄水造成的重力和应力变化.

图1 白鹤滩水电站模拟库区范围红色圆点为历史地震目录(震级大于5级)来自中国地震台网中心. 红色线段为断层, 断层数据来自邓起东等(2003), 加粗红色线段为小江断裂带北段断层, 浅蓝色区域为蓄水水位为海拔825 m时的库区范围.Fig.1 Simulated reservoir area of Baihetan hydropower stationThe red dots denote the catalog of historical earthquakes (magnitude greater than 5) comes from the ChinaEarthquake Network Center. The red line is a fault, and the fault data comes from Deng et al. (2003). The bold red line is the fault in the northern section of the Xiaojiang fault zone, and the light blue area is the reservoir area at the water level of altitude 825 m.
1.2 GRACE-FO数据
GRACE-FO发射于2018年5月22日,是GRACE卫星任务的延续,后者数据发布时间结束于2017年6月29日.该项目依旧是双星系统,利用微波观测星间距变化以反演地球重力场.GRACE-FO卫星同时载荷了试验性质的激光测距装置,为后续卫星任务改进重力场精度提供了数据参考,但GRACE-FO项目的数据分辨率和精度并无明显提高.GRACE-FO的数据处理和发布由GFZ、CSR和JPL三个机构负责,各机构在数据反演方式和参数选取存在不同,故其发布的Level1至Level3数据并不一致,但结果的变化趋势和量级并无明显差异.GRACE-FO数据于2019年7月开始发布.
本研究将利用Level2数据计算白鹤滩地区的重力变化,以方便和模拟计算数据进行对比分析.Level2为球谐系数格式的重力势月解数据,利用连带勒让德函数求和可以获取重力势场,重力场和其梯度场等结果.目前三个机构发布的数据时间从2018年6月1日开始,截止于2020年1月1日,共17个月数据(https:∥podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo).依据前人对不同机构的数据分析可知,对三个机构发布数据取平均值可以有效的减少噪声信号(Sakumura et al., 2014),这种平均策略也得到数据发布机构的认可,故本研究将利用平均值结果开展后续研究.
2 白鹤滩水电站库区重力异常场
为了研究白鹤滩地区的重力异常背景场,本研究利用EIGEN-6C4(Förste et al., 2014)和ETOPO1(Amante and Eakins, 2009)数据获取了该地区的布格重力异常和均衡异常场.首先,利用2190阶次的EIGEN-6C4球谐重力模型计算自由空气重力异常,为了解决超高阶连带勒让德函数的发散问题,在此使用于锦海等(2015)给出的递推公式;其次,对自由空气重力异常进行层间改正和地形改正(Fu et al., 2014)以获取布格重力异常场结果(图2a);最后,基于地形数据和Airy均衡理论,利用球面棱柱体重力正演方法(Uieda et al., 2016)计算了均衡改正,并进一步获取了该地区的均衡重力异常场(图2b).重力改正中使用的地壳和地幔密度取自CRUST1.0模型(Laske et al., 2013),均衡补偿深度选择大陆平均地壳厚度40 km.
白鹤滩水电站临近区域的布格重力异常变化范围为-280~-210 mGal左右,北部和南部地区重力异常值较大,西部和东部地区异常值较小.库区北部布格重力异常大于南部.金沙江流域布格重力异常值为-250 mGal左右.该地区均衡重力异常变化范围为-30~35 mGal左右,此结果与陈石等(2011)给出的Airy均衡异常基本一致.均衡异常不仅反映了地区欠补偿和过补偿的均衡状态,同时也反应着地壳内部横向密度差异引起的重力异常.该地区主要断层两侧存在较大的均衡异常差异,这可能是由于断层两侧的物性差异引起的.库区的均衡重力异常变化范围为-10~10 mGal左右,表明该地区基本处于均衡状态,相对稳定.以上结果为基于重力模型的计算结果,由于目前重力模型中缺失青藏高原及其周边地区的地表观测数据,因此其精度受限.后续研究可进行实地重力观测,以获取精度更高的研究结果.
3 模拟白鹤滩水电站蓄水引起的地表重力变化
水库蓄水造成的重力变化由两部分组成,一部分为蓄水水体负荷造成弹性形变而引起的重力变化,另一部分为蓄水水体的万有引力造成的重力变化.对于两部分的模拟计算,本文将分别使用球体负荷理论和考虑地形的重力计算公式进行模拟研究.
3.1 蓄水负荷弹性形变引起的重力变化
负荷问题研究的是地球在地表质量负荷压力和万有引力作用下的变形响应.研究该问题时,通常首先研究单位质点负荷造成的变形,然后通过积分计算总质量负荷造成的变形(郭俊义, 2000).该研究使用的是格林函数方法,首先将求解变量转换到球谐域,然后把平衡方程、泊松方程、本构关系以及重力势与其梯度的关系式转化为一个微分方程组,之后利用龙格-库塔数值积分和边界条件求解负荷勒夫数,最后对勒夫数进行加权求和以获取格林函数(Longman, 1963; Farrell, 1972; 毛伟建, 1984; 孙文科和李瑞浩, 1986; 汪汉胜等, 1996; 廖彬彬等, 2019).目前球形地球负荷使用较多的方法是由Farrell(1972)给出的,其在前人研究(Longman, 1963)基础上引入渐进解,解决了格林函数的收敛问题,并得到了可用于处理实际问题的格林函数.不同的地球模型对应不同的负荷格林函数,目前使用较多的地球模型为PREM(Preliminary Reference Earth Model)(Dziewonski and Anderson, 1981).

图2 白鹤滩水电站地区布格和均衡重力异常场(a) 布格重力异常场; (b) 均衡重力异常场. 紫色三角形为白鹤滩水电站坝址.Fig.2 Bouguer and isostatic anomaly fields in the Baihetan hydropower station(a) Bouguer gravity anomaly field; (b) Isostatic gravity anomaly field. The purple triangle is the dam site of Baihetan hydropower station.
为了提高弹性变形重力变化的计算精度.首先,提取研究区域对应的CRUST1.0模型数据,用于替换PREM地球模型对应的参数,该方法已经被多个研究证实可以显著提高负荷变形计算的精度(Wang et al., 2013; 贾路路等, 2014; Chanard et al., 2018),替换后模型见图3.其次,利用修改后的地球模型计算负荷勒夫数,并进一步得到负荷格林函数.最后,使用格林函数结合上一节模拟的四个蓄水水位的数据,计算不同水位蓄水引起的弹性形变重力变化,计算点为0.01° × 0.01°的网格数据.四个蓄水水位对应的最大弹性形变重力变化分别为0.008 mGal、0.019 mGal、0.033 mGal和0.039 mGal.
3.2 蓄水水体引起的重力变化
蓄水水体对观测点的重力值是水体万有引力在垂直方向的分量.由于白鹤滩水库库区沿金沙江一带多为峡谷地形,高程变化较为剧烈.因此,在计算重力变化时需要兼顾地形的影响.图4为观测点p和单元水体所在位置q的几何关系.单元水体引起的重力变化可用式(1)计算:
(1)
其中,G为万有引力常数,m为单元长方体水体的质量.rp和rq分别为观测点p和单元水体位置q到地心o的距离,pq为观测点到单元水体的距离.θ为po和qo的夹角,cosθ可根据大圆距离公式计算,表达式为
cosθ=sinφpsinφq+cosφpcosφqcos(λp-λq),
(2)
φp、φq、λp和λq分别为p和q点的纬度和经度.
利用公式(1)计算每个单元水体引起的重力变化,再进行求和即可获取蓄水总量对观测点的重力变化.利用第二节中模拟的四个蓄水数据,分别计算白鹤滩库区的重力变化,四个水位对应的重力变化最大值为0.529 mGal、0.739 mGal、1.093 mGal和1.221 mGal,计算点与负荷弹性形变重力变化一致.蓄水水体引起的重力变化比负荷弹性形变引起的重力变化大了接近两个量级.因此在水库蓄水中,重力变化主要是由蓄水水体的万有引力作用引起的.
将蓄水水体和负荷弹性形变引起的重力变化求和即为白鹤滩水电站蓄水引起的重力变化,如图5所示.图5a—d分别对应蓄水水位为700 m、750 m、800 m和825 m的重力变化空间分布.重力变化较大的位置主要集中于蓄水区附近,重力变化随着距离的增大而快速衰减,蓄水引起的重力变化主要集中在以库区为中心大约30 km的范围内.重力变化较为剧烈的地区集中在巧家以北的金沙江下游地区,金沙江上游地区的重力变化相对较小.造成这种情况的原因是由于下游相较于上游库区周边的地形更为陡峭,水体引起的重力变化较大.
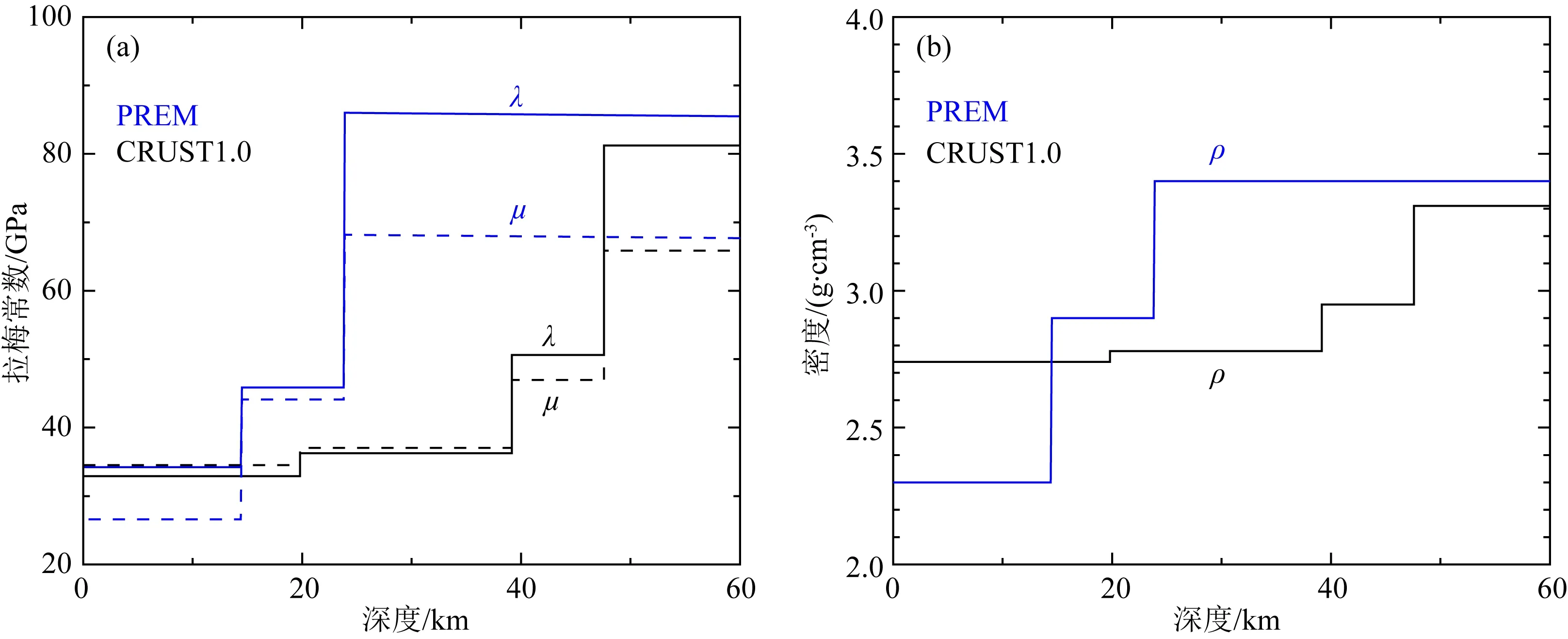
图3 白鹤滩水电站地区CRUST1.0和PREM模型对比(a) 拉梅常数随深度的变化, 其中实线和虚线分别代表拉梅常数λ和μ; (b) 两个模型的密度值ρ随深度的变化. 黑色和蓝色线条分别对应CRUST1.0和PREM模型.Fig.3 Comparison of CRUST1.0 and PREM models in the Baihetan hydropower station(a) The change of Lamé constant with depth, where the solid and dashed line represent the Lamé constant λ and μ, respectively; (b) The change of density value ρ with depth of the two models above. The black and blue lines correspond to the CRUST1.0 and PREM models, respectively.

图4 观测点和单元水体位置的几何关系p和q为观测点和单元水体位置, o为地心, rp和rq分别为观测点p和单元水体位置q到地心的距离.Fig.4 The geometric relationship between the observation point and the unit water body positionp and q are the observation point and unit water body position, and o is the geocentric, rp and rq are the distance from the observation point p and unit water body position q to the geocentric, respectively.
4 GRACE-FO卫星观测的蓄水重力变化
4.1 模拟GRACE-FO卫星观测的蓄水重力变化
通过上文计算已经得到了四个蓄水水位对应的重力变化结果,以上结果是否可以被GRACE-FO探测到,需要进一步的模拟计算研究.由于GRACE-FO的数据为96阶次的球谐系数,同时在以往研究中还进行了滤波平滑以去除南北向条带信号的影响.为了便于和GRACE-FO观测结果进行对比,本研究将上节中模拟计算的重力变化展开为96阶次的球谐系数,并利用各向同性的高斯滤波(Wahr et al., 1998;郑秋月和陈石,2015)和非各向同性的DDK去相关滤波方法(Kusche, 2007; Kusche et al., 2009;郭飞霄等,2018)分别对球谐系数进行滤波平滑处理.之所以使用两种滤波方法是为了验证结果的正确性,以避免由于偶然因素而产生的误判.高斯滤波半径选取340 km,对应的等效去相关滤波矩阵为DDK2,该矩阵已由Kusche等(2009)给出.
基于以上参数,分别对上文中四个蓄水水位引起的重力变化进行球谐展开、阶次截断和滤波处理.由于库区为狭长地带,经过球谐系数展开和滤波,重力变化细节已经消失.因此依据上一节的结果,重力变化较大的区域集中于巧家附近以及下游区域,故在此取巧家位置对应的重力变化结果,进行分析讨论(图6).两种滤波的结果基本一致,DDK滤波结果略小于高斯滤波.四个水位对应的重力变化均在微伽(μGal)量级,700 m水位对应的重力变化达到了1 μGal左右,825 m水位的重力变化达到了5 μGal左右.上文中模拟计算的蓄水引起的重力变化为毫伽量级,可见阶次截断和滤波处理对重力信号的衰减作用可达数千倍.
4.2 GRACE-FO观测结果
为了验证以上模拟的蓄水重力变化是否可以被GRACE-FO卫星探测到,有必要给出研究区域GRACE-FO的观测结果以便进行对比分析.首先对三个机构发布的现有17个月GRACE-FO数据进行平均处理;其次,对平均结果进行C20项替换;最后,使用与模拟数据一致的高斯滤波和DDK滤波去除信号中的条带影响.经过以上数据处理,GRACE-FO在巧家位置的时变重力结果如图7所示.
图7a、b分别为2018年10月份的GRACE-FO数据的DDK和高斯滤波结果,该结果表明两种滤波方法的结果在空间变化趋势上一致,差异主要体现在量级上,在研究区域内高斯滤波的量级比DDK滤波大2 μGal左右.
研究区域2018至2019年的重力变化时间序列(图7c)表明,该地区GRACE-FO观测结果为微伽量级,该重力变化主要是季节性的地表水储存变化引起的.巧家位置高斯滤波的重力变化幅度达到了8 μGal左右,对应的DDK滤波结果为6 μGal左右.虽然两种方法的最大最小值存在差异,但是其变化趋势是一致的.根据图6和图7中模拟结果和GRACE-FO观测结果,可以确定蓄水引起的重力变化与GRACE-FO的观测结果为相同量级.GRACE-FO观测的最大重力变化速率为每月2~3 μGal左右,而蓄水引起的重力变化为1~5 μGal.若蓄水在较短时间内完成,GRACE-FO可以捕捉到该重力变化信号.鉴于三峡库区曾在2003年的2个月内完成60 m左右的蓄水,白鹤滩地区对应该蓄水水位引起的重力变化约为2 μGal(图6),所以蓄水引起的重力变化与GRACE-FO观测结果的每月变化速率接近,为了提取蓄水引起的重力变化,需要引入其他数据以扣除白鹤滩地区的季节性重力变化.詹金刚和王勇(2011)利用GRACE和GLDAS(Global Land Data Assimilation System)模型数据给出了龙滩水电站水库蓄水可产生约2.17 μGal的重力变化,与本研究估计的白鹤滩库区蓄水引起的重力变化相近.同时,他们的研究指出GLDAS模型的结果主要表现为季节变化特征,对库区重力变化趋势没有明显贡献,因此后续研究中可以利用GLDAS模型数据去除GRACE观测中的周期信号,以获取蓄水引起的重力变化.金沙江上下游还存在库容较大的水电站,这些水电站的水位变化也会对GRACE-FO的观测结果造成影响,这部分研究将在白鹤滩水电站蓄水后进行探讨.

图5 白鹤滩水电站蓄水引起的地表重力变化(a)、(b)、(c)和(d)分别对应蓄水水位为700 m、750 m、800 m和825 m的重力变化空间分布. 黑色等值线和颜色代表蓄水引起的重力变化.Fig.5 Gravity changes on the surface caused by the impoundment in Baihetan hydropower station(a), (b), (c), and (d) correspond to the spatial distribution of gravity changes with water levels of 700 m, 750 m, 800 m and 825 m, respectively. The black contours and color denote the gravity change caused by the impoundment.

图6 模拟GRACE-FO卫星观测的蓄水重力变化四个水位蓄水引起的重力变化经过球谐展开和滤波处理后的结果.Fig.6 Gravity changes of the impoundment by simulating GRACE-FO satellitesThe results of the gravity changes caused by the impoundment of the four water levels after spherical harmonic expansion and filtering.
5 白鹤滩水电站蓄水引起的库仑应力变化
库区蓄水不仅会造成重力变化,还会造成地壳内部应力的变化.在此基于上文中改正后的分层地球模型,利用球体负荷理论计算了研究区域由于蓄水而引起的地壳内部应力变化,并进一步获取了与水库临近的小江断裂带北段断层面上的库仑应力变化.小江断裂带北段断层紧邻金沙江,并且与库区呈平行分布(图1),因此蓄水造成的应力变化对该断层的影响最大.同时,该地区5级以上地震也主要沿着该断层的走向分布,故模拟其库仑应力变化,进而给出触发地震的可能性分析是非常有必要的.小江断裂带北段断层的几何参数取自宋方敏和俞维贤(1998)给出的结果,断层为左旋走滑,走向为340°,倾向为东北,倾角为80°.库仑应力的计算公式为

图7 GRACE-FO重力数据空间分布和时间序列(a) DDK滤波后的2018年10月GRACE-FO重力数据空间分布; (b) 高斯滤波后的2018年10月GRACE-FO重力数据空间分布; (c) 巧家位置的GRACE-FO重力变化时间序列.Fig.7 The spatial distribution and time series of GRACE-FO gravity data(a) The spatial distribution of GRACE-FO gravity data in October 2018 after DDK filtering; (b) The spatial distribution of GRACE-FO gravity data in October 2018 after Gaussian filtering; (c) The time series of GRACE-FO gravity change at the location of Qiaojia.
ΔCFS=Δτ+μ′Δσn,
(3)
其中Δτ和Δσn为蓄水引起的断层面上的剪切应力和正应力变化(Xu et al., 2010;徐晶等,2013).μ′为有效摩擦系数,取值为0.4(King et al., 1994).利用公式(3)结合断层的几何参数计算了四个蓄水水位对应的断层面上的库仑应力变化,计算结果如图8所示.
小江断裂带北段断层面上蓄水引起的库仑应力变化结果表明,随着蓄水水位的增长,库仑应力变化的量值和影响范围逐渐增大.库仑应力变化的最大负值和正值分别达到了-0.06 MPa和0.07 MPa,其变化较为剧烈的区域主要位于巧家以南和以北地区.巧家以南地区是蓄水量最大的地区,巧家以北地区断层跨过库区(图8e),因此库仑应力变化较为复杂,呈现正负交替分布(图8a—d).Ge等(2009)模拟计算了紫坪铺水库蓄水100 m时的地壳内部弹性应力变化,给出了临近断层面上的库仑应力变化量值为-0.5~0.05 MPa左右,与本研究计算结果的量级接近(图8d).
图8中等值线代表大于0.01 MPa的范围,该值为可能触发地震的阈值(King et al., 1994).随着蓄水量的增加,巧家南部地区大于该阈值的范围逐渐增大,深度从大约2 km增长为20 km左右,宽度从大约0 km增长为25 km左右;巧家北部地区大于阈值的区域较小,深度和宽度均小于10 km(图8).依据以上分析,白鹤滩水电站蓄水会在小江断裂带北段断层临近巧家南部和北部地区形成大于地震触发阈值的区域(图8e).然而,以上模拟研究并未考虑孔隙压等其他因素的影响.孔隙压变化又涉及到研究区域与孔隙压扩散系数相关的地质和水文等因素的影响(刘耀炜等2011),因此未来的细化研究不仅需要了解该地区的岩性特征,还需要对该地区实际蓄水过程中的库区水位、重力和地下水位进行详尽观测以约束该地区的地下水分布情况,从而获取合理的孔隙压结果,以便为蓄水触发地震的可能性研究提供参考.
6 结论
本研究计算了白鹤滩水电站周边地区的均衡重力异常与四个水位蓄水对应的地表重力变化,模拟了GRACE-FO卫星可能观测到的区域重力变化,还获取了蓄水过程在小江断裂带北段上产生的库仑应力变化,得到如下主要结论:
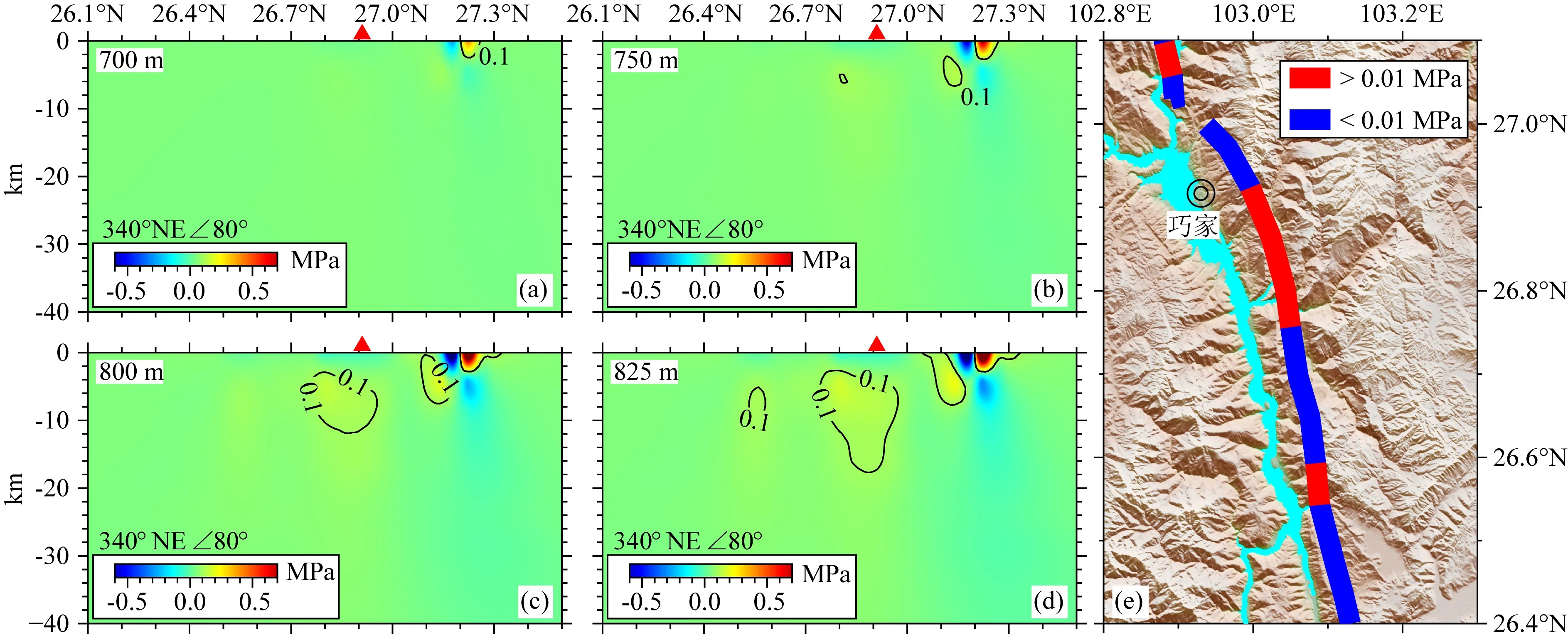
图8 白鹤滩水电站蓄水引起的小江断裂北段库仑应力变化(a)、(b)、(c)和(d)分别为水位700 m、750 m、800 m和825 m时对应的小江断裂带北段断层面库仑应力变化; (e)为(d)对应的5 km深度的库仑应力结果.红色线段代表库仑应力大于0.01 MPa,蓝色线段代表库仑应力小于0.01 MPa. 浅蓝色区域为蓄水水位为海拔825 m时的库区范围.Fig.8 Coulomb stress changes in the northern section of the Xiaojiang fault caused by the impoundment of Baihetan hydropower station(a), (b), (c) and (d) are the Coulomb stress changes at the fault plane in the northern section of the Xiaojiang fault zone corresponding to the water levels of 700 m, 750 m, 800 m and 825 m, respectively; (e) is the corresponding Coulomb stress result at a depth of 5 km in (d). The red lines denote the Coulomb stress is bigger than 0.01 MPa, and the blue lines denote the Coulomb stress is smaller than 0.01 MPa. Light blue area is the reservoir area at the water level of altitude 825 m.
(1)白鹤滩库区的均衡重力异常变化范围为-10~10 mGal左右,表明这一地区基本处理均衡状态,较为稳定.
(2)四个模拟水位的重力变化表明,库区水体负荷造成的弹性形变引起的重力变化为0.008~0.039 mGal,蓄水水体万有引力造成的重力变化比弹性形变结果大两个量级,为0.529~1.221 mGal,蓄水水体的万有引力作用为库区重力变化的主因.
(3)模拟GRACE-FO重力变化表明,白鹤滩地区蓄水引起的卫星观测重力变化约为1~5 μGal.2018—2019年间GRACE-FO观测到的最大重力变化速率约为每月2~3 μGal左右,因此GRACE-FO有可能观测到白鹤滩水电站蓄水过程伴随的重力变化.
(4)水电站库区蓄水将在巧家以南和以北地区形成库仑应力变化大于触发地震阈值的区域,该区域诱发地震的可能性较高,需密切关注.

