垂直井筒内超临界蒸汽流动过程中的传热特性计算与分析

庞占喜，高 辉，张泽权，王陆亭

（1.油气资源与探测国家重点实验室，北京 102249；2.中国石油大学（北京）石油工程学院，北京 102249；3.中国中化集团有限公司中化能源物流有限公司，北京 100031）

中国稠油资源储量丰富，如何高效开采稠油资源仍是目前面临的主要难题［1-2］。超临界蒸汽因其高热量和特殊性质，在热力采油上具有很大的发展前景。20 世纪60 年代RAMEY 最先建立了井筒传热的数值计算模型［3］，但是该模型只适用于单相流，而后SAGAR 等对RAMEY 的模型进行改进［4］，使其适用于多相流。1965 年，SATTER 把从井筒到地层间传递热量的过程分成从井筒到水泥层的稳定传热与从水泥层到地层间的非稳定传热2 部分，但是假设蒸汽压力没有损失且按照一维径向流来处理传热问题［5］。1972 年，PACHECO 等进一步改进了SATTER 的模型，在计算压力损失时，对地层中的非稳态传热采用二维轴对称模型［6］。中外已对超临界蒸汽有一定的研究。1966 年，SHITSMAN 对垂直管内超临界蒸汽的传热进行了系统的实验研究［7］。1970 年，NOWAK 等对超临界蒸汽在水平圆管内的流动换热特性进行了理论研究［8］。2000 年，张毅等对超临界蒸汽在注汽井筒内的参数变化进行了模拟计算，但将超临界蒸汽视为理想气体［9］。超临界蒸汽在井筒流动过程中，由于井筒热损失，其可能变成过热蒸汽、湿蒸汽甚至热水。所以，研究超临界蒸汽在井筒内的流动特性及热传递规律对该流体在稠油油藏热采中的应用显得尤为重要［10-11］。笔者首先采用IAPWS-IF97 工业标准［12］建立了超临界蒸汽的物理化学参数计算方法，在此基础上建立了一套超临界蒸汽在垂直井筒内的流动过程及热传递计算模型，对超临界蒸汽在稠油油藏热采中的应用与推广具有重要的理论意义。

1 超临界蒸汽物理化学特性

不同温度、压力条件下水的状态可分为4 个区（图1a），分别为固态区、过饱和水区、过热蒸汽区和超临界区；过饱和水区与过热蒸汽区之间的界限为饱和线，饱和线起始于三相点（温度为0 ℃，压力为0.101 MPa），结束于临界点（温度为374.15 ℃，压力为22.12 MPa）；当温度、压力同时超过临界点时，水处于超临界状态。在超临界区，因高温而热膨胀的水相密度和因高压而被压缩的蒸汽密度正好相同时的蒸汽被称为超临界蒸汽［13-14］。

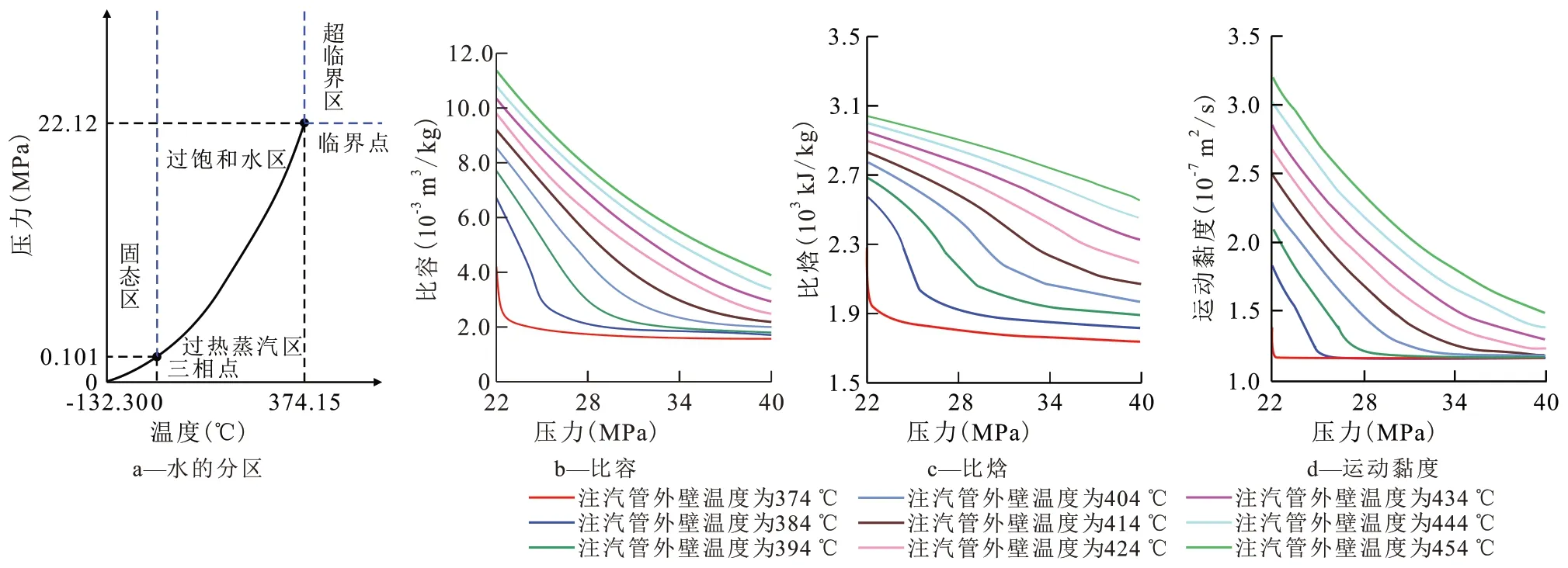
图1 水的分区及超临界蒸汽的物化参数Fig.1 Partition of water regions and physicochemical parameters of supercritical steam

超临界蒸汽的物理化学参数是进行井筒热传递计算的基础，采用IAPWS-IF97 水和水蒸汽性质工业标准及其补充模型［12］，完善超临界蒸汽的物理化学参数计算方法，以便于开展井筒内流动规律及换热损失的研究。利用超临界蒸汽的无因次吉布斯自由能方程推导得到热物性参数，如超临界蒸汽的密度（比容的倒数）和比焓的表达式分别为：

其中：

（1）和（2）式中的无因次吉布斯自由能系数和指数来源于对无因次吉布斯函数的回归，具体取值见文献［12］。在此基础上，基于ITS-90 温标和IAP⁃WS-IF97 计算得到的密度值，根据不同的温度与压力值可迭代计算出对应的运动黏度值，再将运动黏度与密度相乘则可得到动力黏度值。计算得到超临界蒸汽的比容、比焓、运动黏度等热物性参数曲线（图1b—1d），为下一步进行超临界蒸汽在井筒中的流动特性及传热规律分析提供基础数据。

2 数学模型与验证

2.1 基本假设

超临界蒸汽在井筒的流动过程中，从井筒到地层的传热过程可分成2部分（图2），第一部分是由注汽管中心到水泥环外缘的一维稳定传热，第二部分是由水泥环外缘到地层间的一维不稳定传热［15］。超临界蒸汽井筒沿程热损失计算自井口开始，其基本假设包括：①井口处超临界蒸汽的参数（速率、压力、温度）保持不变，地表温度恒定。②垂直井筒中蒸汽的流动是等质量流。③垂直井筒底部使用封隔器，确保蒸汽不窜入油套环空，油套环空中充满导热系数恒定的某种流体。④注汽井井筒内的蒸汽为一维流动，且同一截面处蒸汽的压力、温度相等。⑤不考虑沿井身方向的纵向传热。

图2 超临界蒸汽流动过程对应井筒结构剖面Fig.2 Profile of wellbore structure corresponding to supercritical steam flow

2.2 数学模型建立

根据以上假设，自垂直井筒中心经注汽管内管、隔热管、注汽管外管、油套环空、套管、水泥环后再经过地层的传热过程需要分成2部分分别计算。

2.2.1 自注汽管中心到水泥环外缘稳定传热过程

自注汽管中心到水泥环外缘单位时间内dz微元长度上的热流量表达式为：

2.2.2 自水泥环外缘至地层间的不稳定传热过程

计算水泥环外缘到地层间的不稳定传热时，引入时间变量，因传热量与时间成反比，则自水泥环外缘至地层间单位时间内dz微元长度上的热流量表达式为：

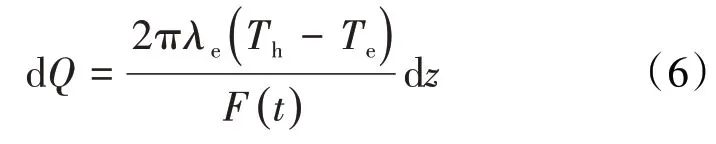
其中：

F（t）表达式可根据SATTER计算模型给出［5］：

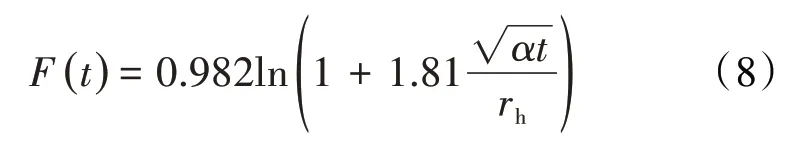
根据能量守恒原理，自注汽管中心至水泥环外缘所传递的热量等于水泥环外缘至地层间所传递的热量，将（5）式、（6）式合并，可得：

2.2.3 相关方程

注汽管内一维流动的动量方程为：

其中，重力项、摩擦损失项、加速损失项的表达式分别为：

超临界蒸汽的特殊物理化学性质造成其流动特征完全不同于常规湿蒸汽，因其处于高温高压状态下的高速流动，必须对加速度损失项进行修正。有些研究者将超临界蒸汽视为理想气体进行计算，势必造成较大的计算误差［9，16-18］。有的学者提出了适用于超临界蒸汽管流沿程摩擦损失梯度的计算式为［19］：

在超临界条件下，考虑气液两相处于单一相态的特征，对摩擦损失项化简变形得：

其中：

（15）—（18）式充分体现了超临界蒸汽物化性质对所受摩擦力的影响。

注汽管内一维流动的能量方程为：

经推导，得到能量守恒方程为：

计算井筒总热阻时，除考虑油套环空内的对流换热与辐射换热外，超临界蒸汽在注汽管内的高速流动也使得注汽管内壁处存在对流换热效应，因此引入注汽管内壁处的对流换热系数来进一步修正总热阻。这也是不同于其他文献中关于井筒热损失计算的一种修正。井筒总热阻的表达式为：

其中的辐射传热可表达为：

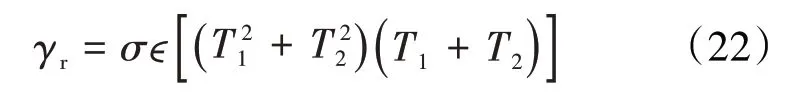
2.3 求解思路

垂直井筒中超临界蒸汽在流动过程中的热损失计算流程包括：①针对井筒选择合适的井段长度（Δz）、时间步长（Δt）和温度变化值（ΔT），首先令压力降（Δp）为0，计算相应的超临界蒸汽的比容、比焓及运动黏度。②采用（10）式计算压力变化微分量（dp），并计算相应的超临界蒸汽的比容、比焓及运动黏度。③采用（21）式计算井筒总热阻，再利用（9）式计算水泥环外缘温度。④根据自注汽管中心到注汽管外壁导出的热量与注汽管外壁到套管内壁导出的热量相等的原理，计算注汽管外壁温度和套管内壁温度。⑤利用（20）式计算超临界蒸汽的焓值变化微分量（dHcs），从而得到温度变化微分量（dT），判断|dT-ΔT|是否小于误差ε；若满足要求则进行步骤⑥，否则令ΔT=dT，返回步骤①重新迭代。⑥选择下一个井段，按照步骤②—⑤进行迭代计算，直至计算到井底为止。⑦选择下一个时间段，按照步骤①—⑥进行迭代计算，直至计算注汽结束为止。

2.4 模型验证

文献［9］将超临界蒸汽处理为理想气体，文献［10］中摩擦损失计算采用了分散流型摩擦压降系数法，基于文献［9-10］中所采用的数学模型和计算参数，井口注入温度为400 ℃，注入压力为25 MPa，注汽速率选择12 t/h，再利用（1）式、（2）式及（5）—（22）式计算得到井筒沿程的温度和压力。采用的热物性参数及井筒尺寸如表2 所示。由计算结果（图3）可见，本文计算得到的温度和压力变化趋势与文献［9-10］中的计算结果变化趋势一致；在注汽速率为12 t/h 的情况下，本文模型与文献［9］模型间的温度误差为0.367%，压力误差为0.678%；本文模型与文献［10］模型间的温度误差仅为0.018%，压力误差仅为0.243%，可见本文结果与文献［10］结果之间的误差更小。本文与文献［10］都是基于超临界蒸汽的物理化学参数，均考虑了超临界蒸汽在井筒中流动时的质量守恒、动量守恒与能量守恒三大原理，本文与文献［10］的差异在于本文对井筒内超临界蒸汽流动时的摩擦损失计算中也充分考虑了超临界蒸汽的特殊性质，然而文献［9］中将超临界蒸汽视为理想气体，其计算结果与另外2 种模型的计算结果差异较大。

表2 相关热物性参数及井筒尺寸数据Table2 Related thermophysical properties and wellbore dimension

图3 本文计算结果与文献计算结果验证对比Fig.3 Comparison between calculation results in this paper and those in literatures

3 影响因素分析

3.1 注汽压力

井身长度选取1 000 m，注汽时间选取15 d，在定质量流量和井口温度的条件下，由不同注汽压力时井筒沿程温度与压力变化（图4）可以看出，当注入压力分别为23，24 和25 MPa 时，井筒内的压力均随井深的增加而逐渐增加，然而温度却随着井深的增加而逐渐下降，并且初始注汽压力越高，在相同长度井段内压力的增值越大，而温度降低幅度逐渐减小；当注汽压力为25 MPa时，井深为1 000 m 处的温度降低幅度仅为0.43%，而当注汽压力为23 MPa时，井深为1 000 m 处的温度降低幅度却达1.71%。因此，在相同注汽温度条件下，升高注汽压力有利于维持井底较高的蒸汽温度而使蒸汽保持超临界状态。

图4 不同注汽压力时井筒沿程温度与压力变化Fig.4 Temperature and pressure changes along the wellbore under different steam injection pressures

3.2 注汽温度

在定质量流量和井口压力（25 MPa）的条件下，由不同注汽温度时井筒沿程温度与压力的变化（图5）可知，当井口注汽温度分别为400，425 和450 ℃时，初始注汽温度越高，温度下降越快，同时压力升高越快；而当注汽温度为400 ℃时，井筒沿程温度随井深增加而出现略有降低趋势，井深为1 000 m 处的温度降低幅度仅为0.45%，而当注汽温度为450 ℃时，井深为1 000 m 处的温度降低至426.7 ℃，降低幅度达到5.17%，但井底仍保持高温状态。可见，提高注汽温度有利于维持较高的井底温度而使蒸汽保持超临界状态。

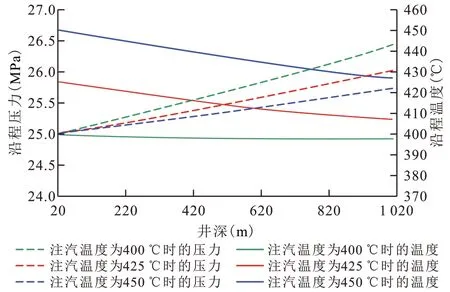
图5 不同注汽温度时井筒沿程温度与压力变化Fig.5 Temperature and pressure changes along the wellbore at different steam injection temperatures

3.3 注汽速率

注汽温度选择400 ℃，注汽压力选择25 MPa，研究注汽速率对井筒沿程温度与压力的影响。由计算结果（图6）可知，当注汽速率低于2 t/h 时，超临界蒸汽在井筒中流动时会发生相态转变，相态转变的深度约为1 000 m，呈现为压力快速上升而温度大幅下降的趋势，即此时的水转变为超高温热水，处于过饱和水区（图1a）。随注汽速率的升高，转相点逐渐消失，当注汽速率超过4 t/h 时，完全满足井深为1 000 m的垂直井的井底蒸汽为超临界状态的要求。当注汽速率过低时，图6 中温度变化曲线的切线斜率随井深不断发生改变，这种现象可根据超临界蒸汽的物理化学特性进行分析。在注汽速率一定的情况下，超临界蒸汽在井口附近所受压力小，使得蒸汽密度小，所以在单位时间内通过注汽管的注汽速率就大，即蒸汽流速高，使得蒸汽内部、蒸汽与注汽管内壁之间的能量损失严重，因此自井口至200 m 井深范围内的井筒沿程温度下降快，温度曲线斜率大；而当蒸汽进入深层注汽管后，蒸汽压力升高，低流速时甚至变为热水状态，其流动过程中的热损失速率进一步增加，造成温度下降幅度进一步加大，温度曲线斜率增加［15-16］。

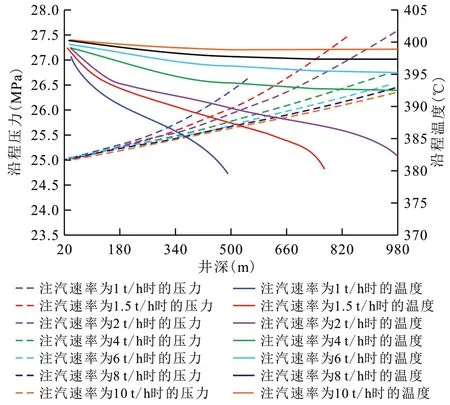
图6 不同注汽速率时井筒沿程温度与压力变化Fig.6 Temperature and pressure changes along wellbore at different steam injection rates

3.4 注汽时间

注汽压力选择25 MPa，注汽温度选择400 ℃，注汽速率选择6 与8 t/h，注汽时间分别选择1，15 和30 d，研究注汽时间对井筒沿程温度变化的影响。由计算结果（图7）可见，注汽速率保持不变时，随着天数的增加，井筒内温度逐渐上升；在注汽初期，井筒温度上升速度快，而随着注汽时间的增加，井筒温度逐渐趋于稳定，当注汽时间超过15 d 后，井筒内温度分布基本达到稳定状态。随着注汽速率的增加，井筒沿程温度呈现明显增加趋势，即提高注汽速率有助于减少井筒热损失，有利于维持井底蒸汽处于超临界状态［16］。

图7 不同注汽时间时井筒沿程温度的变化Fig.7 Temperature changes along wellbore over different steam injection time

3.5 井深

当注汽速率选择8 t/h 时，随井深的增加，井筒沿程蒸汽压力逐渐增加，井筒沿程温度先降低而后在井深约为850 m 处开始增加，而当回升一定范围后出现了温度的峰值，至约2 300 m 处又逐渐降低（图8a）。在温度曲线的第一个谷底处，蒸汽密度在此处会增大很快，然后趋于平缓，使得井筒中部温度降低趋于平缓；而当蒸汽达到深层之后，此时井筒压力过大，蒸汽流速减小，能量损失速率进一步扩大，造成温度曲线斜率再一次增加。分析其原因为：在井筒前段处，起主导作用的是热传导和对流换热，蒸汽温度逐渐下降；当蒸汽进入深层井筒时，井筒压力不断上升，此时井筒内压力过大，使得超临界蒸汽密度增大，蒸汽分子之间产生了相对运动，造成温度出现回升现象［20］。由3 种不同注汽速率（4，8 和12 t/h）在3 000 m 井筒内的温度变化（图8b）可知，不同注汽速率条件下井筒温度的变化趋势不同，注汽速率较低时（4 t/h）井筒温度下降幅度大，其原因为注汽速率低，蒸汽体积流量小，单位时间内经井筒进入地层的热损失速率大，至一定深度后蒸汽出现转相点而变为纯水相，注汽速率为4 t/h时的相态转变深度约为2 150 m，而当注汽速率超过8 t/h时，在井口至3 000 m深度范围内未出现相态转变点。因此，低流速时经热传导和对流换热的热损失对超临界蒸汽的流动特性影响程度更大。而当蒸汽速率为12 t/h 时，井筒沿程温度略有下降后而逐渐增加，说明高注汽速率有助于提高井筒内超临界蒸汽的温度，并有助于维持其超临界状态。

图8 井深为3 000 m时井筒沿程压力和温度的变化Fig.8 Temperature and pressure changes along wellbore at well depth of 3 000 m

4 结论

基于超临界蒸汽的特性，运用IAPWS-IF97 水和蒸汽性质工业标准及其补充模型，实现超临界蒸汽的物理化学性质的数学描述。在此基础上，建立超临界蒸汽在垂直井筒中流动时的热损失计算数学模型，该模型综合考虑超临界蒸汽的物理化学性质、超临界蒸汽的质量守恒、动量守恒与能量守恒以及超临界蒸汽在井筒中流动时的导热规律。

分析了超临界蒸汽井筒流动与热损失的影响因素，包括注汽压力、注汽温度、注汽速率、注汽时间、井深等。井筒内超临界蒸汽的压力随井深的增加而增加，而温度却随着井深的增加而逐渐下降；当注汽温度为400 ℃时在1 000 m 处的温度降低幅度为0.45%，注汽温度为450 ℃时温度降低幅度达到5.17%；升高注汽压力或增加注汽温度均有利于维持井底蒸汽的超临界状态。

超临界蒸汽流动过程中，井筒内蒸汽压力快速上升而温度大幅度下降，随井深的增加压力逐渐增加，而井筒内温度呈现波动特征甚至相态转变特征。如果注汽速率过低或井筒深度过大，造成超临界蒸汽转变为纯水状态，处于过饱和水区；当注汽速率为2 t/h时的相态转变深度约为1 000 m，而注汽速率为4 t/h时的相态转变深度约为2 150 m。

符号解释

a——温度梯度，℃/m；

A——流动面积，m2；

dp——压力变化微分量，MPa；

dHcs——超临界蒸汽的焓值变化微分量，kJ/kg；

dQ——单位时间内dz微元长度上的热流微分量，J/s；

dT——温度变化微分量，℃；

dz——垂直井筒的微元长度，m；

f——阻力系数；

f0——不考虑浮力时的强迫对流摩擦阻力系数；

fv——考虑重力加速效应的流动摩擦阻力系数；

g——重力加速度，m/s2，取值为9.8；

Hcs——超临界蒸汽的比焓，kJ/kg；

i——无因次吉布斯自由能系数或指数的取值标号；

ics——超临界蒸汽的质量流速，kg/s；

Ii——无因次吉布斯自由能压力指数；

Ji——无因次吉布斯自由能温度指数；

ni——无因次吉布斯自由能系数；

p——压力，MPa；

p*——参考压力，MPa，取值为1；

pr——无因次压力；

Δp——压力降，MPa；

Q——单位时间内的热流量，J/s；

r1——注汽管内管半径，m；

r2——隔热管内半径，m；

r3——隔热管外半径，m；

r4——注汽管外管半径，m；

rci——套管内半径，m；

rco——套管外半径，m；

rh——水泥环外缘半径，m；

R——气体常数，J/（K∙mol），其值为8.314；

Re——雷诺数；

t——注汽时间，s；

T——绝对温度，K；

T1，T2——油套环空内、外界面温度，℃；

T*——参考温度，K，取值为540；

Te——地层温度，℃；

Th——水泥环外缘温度，℃；

Tm——地表温度，℃；

Tr——无因次温度；

Ts——蒸汽温度，℃；

Δt——时间步长，s；

ΔT——温度变化值，℃；

vcs——超临界蒸汽的流动速度，m/s；

W——单位时间内摩擦力所做功，J/s；

Δz——井段长度，m；

z——井深，m；

α——热扩散系数，m2/s；

γ1——注汽管内壁处的对流换热系数，W/（m2·℃）；

γc——油套环空内对流换热系数，W/（m2·℃）；

γr——油套环空内辐射换热系数，W/（m2·℃）；

ε——误差，℃；

ϵ——黑度，一般取0.7；

θw——井筒总热阻，（m∙s∙℃）/J；

λcas——套管导热系数，W/（m·℃）；

λcem——水泥环导热系数，W/（m·℃）；

λe——地层导热系数，W/（m·℃）；

λins——绝热层材料导热系数，W/（m·℃）；

λtub——注汽管导热系数，W/（m·℃）；

μcs——超临界蒸汽的黏度，mPa∙s；

μw——水的黏度，mPa∙s；

ρcs——超临界蒸汽的密度，kg/m3；

ρw——水的密度，kg/m3。

σ——辐射系数，W/（m2·℃4），可取值为0.000 88；

τf——超临界蒸汽管流沿程摩擦损失梯度，Pa/m。