基于PSO-SQP算法的空地导弹弹道优化

杨光宇，陈国光，王 捷，朱豪坤

(中北大学 机电工程学院， 太原 030051)

空地导弹是军事战争中使用范围广、消耗量大、用途多的武器类型[1]。随着作战任务及打击目标的多样化，对空地导弹弹道轨迹也提出了更高的要求。弹道优化设计是现代导弹设计中的重要内容，有利于提高导弹飞行品质以满足既定任务要求。对导弹设计有着十分重要的意义及实际工程价值[2-3]。

弹道优化设计，实质就是求解在满足各种约束条件下的最优控制问题，同时也是一个动态优化问题。弹道优化的方法主要分为直接法和间接法两大类[4-5]。直接法是将连续的优化问题直接离散并进行参数化，不需要求解出最优值的条件。间接法是基于极大值原理将最优控制问题转换为哈密顿边值问题[6]。伪谱法是数值法的典型代表方法，大多数配点是基于高斯积分规则[7]。高斯伪谱法作为一种基于全局插值多项式的直接配点法，它相对于一般直接配点法的优势是可以用较少的节点获得较高的精度[8]。

本文利用高斯伪谱法将最优控制问题(动态优化问题)转化为非线性规划问题，SQP算法因其稳定性和精度优势在求解此类问题上应用最为广泛。但SQP算法对初值依赖度很高，如若随意选取初值，很难求得最优解[9]。粒子群算法对目标函数和应用条件的限制较少，而且收敛速度快，具有更大的灵活性和适应性[10]，因此本文利用全局寻优能力较强的粒子群算法快速求解一条优化弹道作为初值，而后代入SQP算法求解该问题。

1 问题描述

空地导弹弹道优化设计问题是一类复杂的多约束动态优化问题，问题描述包括目标函数、约束条件和优化变量等。一般最优控制问题的Bolza形式描述如下式：

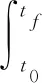
(1)

其中，u(t)∈Rm为控制变量；x(t)∈Rn为状态变量；t0和tf为时间的初值和末值，可固定也可自由。

系统满足的动力学约束、边界条件约束和路径约束分别为

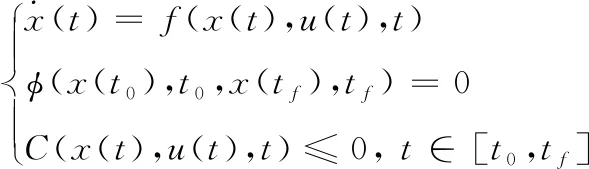
(2)

期望得到一条用时最短且满足约束的弹道，故目标函数选取终端时刻，即

minJ=tf

(3)

方案弹道初步设计过程中简化了运动模型，将导弹描述为理想的质点，暂时不考虑弹体绕质心转动的影响，以纵向平面内的质心运动方程为动力学约束[11]。

动力学约束方程如式(4)所示，式中:m为导弹质量；P为发动机推力；ISP为发动机比冲；mc为质量流量；X=qsCx、Y=qsCy分别为阻力和升力，q为动压，s为参考面积，Cx、Cy分别为阻力和升力系数，两者均是马赫数Ma和攻角α的函数，可由吹风试验和数值计算获得；ϑ为导弹俯仰角；θ为弹道倾角；x、y分别为射程和飞行高度。

(4)

边界约束条件主要包括终端时刻的射程x和飞行高度y。

(5)

路径约束条件主要包括飞行过程中的动压q、法向过载ny和控制变量(攻角)α的约束。

(6)

2 高斯伪谱法

高斯伪谱法以Legendre多项式的根为离散点，将连续最优控制问题的状态变量和控制变量离散化，并以离散点为节点采用全区间Lagrange插值多项式来近似状态变量和控制变量，从而将动力学方程等约束转化为代数约束，形成非线性规划问题[12-13]。

高斯伪谱法的基本算法过程如下：

1) 对时间变量t作变换到τ∈[-1，1]上。

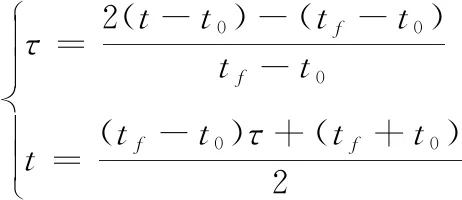
(7)

动力学方程约束式(2)转化为

(8)

2) 取N阶Legendre多项式N的个根τk∈(-1，1)，k=1，2，…，N；再令τ0=-1，τf=1，则τ0，τk，τf构成弹道的N+2个离散点。

3) 将状态变量与控制变量在离散点上离散化，从而将动力学方程约束、边界条件约束和路径约束转化为代数约束。

由高斯伪谱法的算法过程可得：

(9)

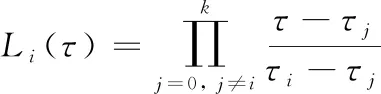
对式(9)求导：

(10)

将式(10)代入式(8)，得到状态向量在配点上应满足的代数约束：

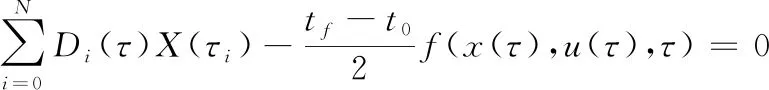
(11)

由式(8)可得：

(12)

采用高斯积分公式近似式(12)中的积分项，可得离散化终端边界条件：

(13)

把边界条件和过程约束也离散化，将弹道优化问题转化为非线性规划问题。其一般形式描述如下式：

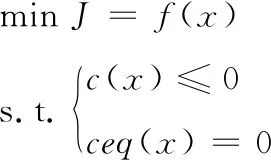
(14)

其中，c为非线性不等式约束;ceq为非线性等式约束。

3 粒子群算法

粒子群算法是计算智能领域，除了蚁群算法、鱼群算法之外的一种群体智能的优化算法。该算法最早由Kennedy和Eberhart在1995年提出的。粒子群算法源于对鸟类捕食行为的研究，鸟类捕食时，找到食物最简单有效的策略就是搜寻当前距离食物最近的鸟的周围区域。

粒子群寻优算法中每个粒子追随个体极值和全局极值的过程进行信息更新[14]，同时也代表优化问题的一个潜在解，用位置、速度和适应度值三项指标表示该粒子特征。

粒子的适应度值由适应度函数决定，其值表示了粒子的优劣。粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整。粒子的位置随着自身位置及速度进行动态调整。从而实现个体在可行解空间中的寻优。

粒子的速度和位置更新公式分别为[15]：

(15)

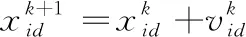
(16)

设向量X={α1，α2，…，αn，tf}为优化问题的一个潜在解，即为粒子群算法中的一个粒子。其中前n维为攻角的变化值，最后一维tf为终端飞行时间(粒子的维数为n+1)，换言之每个粒子都代表了攻角随时间变化的一种规律。

初始化粒子群，设定种群规模(Sizepop)、最大进化代数(Maxgen)、惯性权重、加速度常数、位置和速度的上下限等。通过适度函数计算出n维的所有状态变量值，进而求出每个粒子的适度值，保存个体和群体经历的最优位置，更新粒子的速度和位置，重复上述过程，直到满足终止条件。将得到的最优值拟合成一条连续弹道，然后在得到的弹道曲线上用高斯伪谱法的取点规则取点，得到SQP算法的初值X0，代入求解非线性规划问题，得到最终优化设计弹道，算法流程如图1所示。

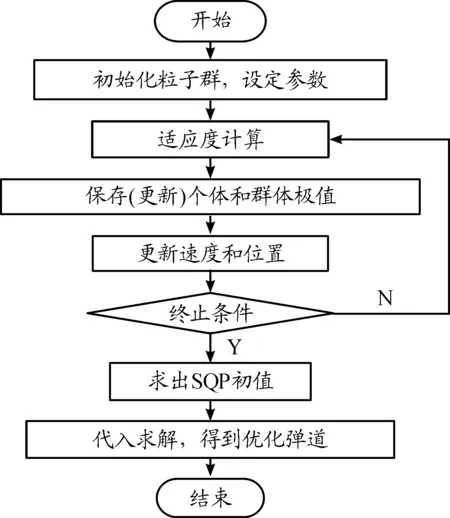
图1 算法流程框图

4 仿真结果与分析

结合某型空地导弹弹道仿真结果和算法流程图，粒子群算法各个参数的初值如下：Maxgen=50，Sizepop=20，c1=c2=1.45，ω=0.8，t0=0。空地弹道方案优化设计条件为：x(τ0)=0，y(τ0)=7 000，m(τ0)=225，x(τf)=14 000，y(τf)=0，nymax=15，αmax=0.2 rad。适应度函数的功能是通过粒子X={α1，α2，…，αn，tf}计算出状态变量的变化规律，最后适度值的大小表明了初始弹道最终与目标点距离的远近。

粒子的维数为n+1，n的值可任意选取，但不宜过大或过小。

以n取为20、30和40为例，算法进化曲线如图2所示，仿真结果如图3和图4所示。

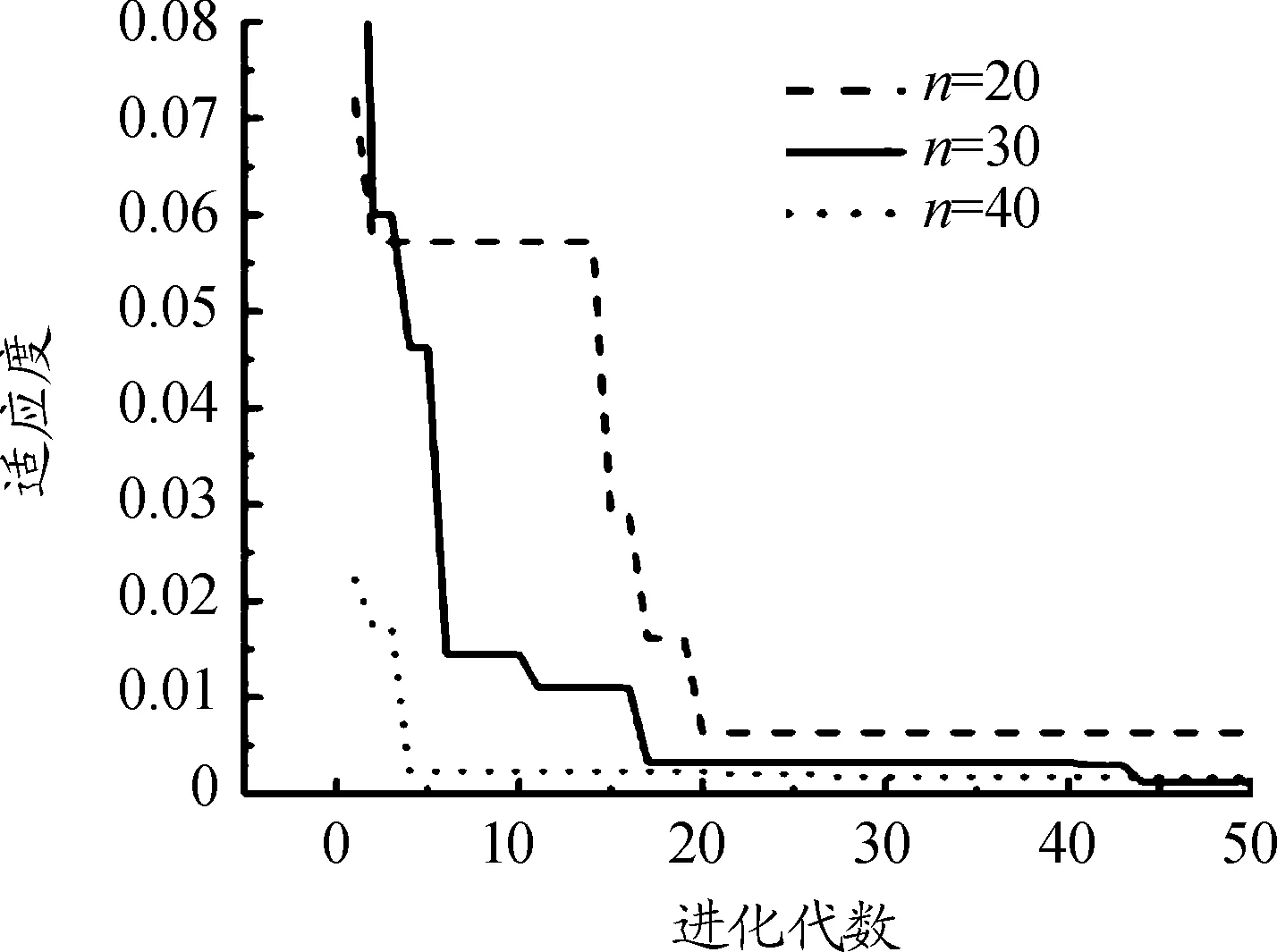
图2 粒子群算法进化曲线

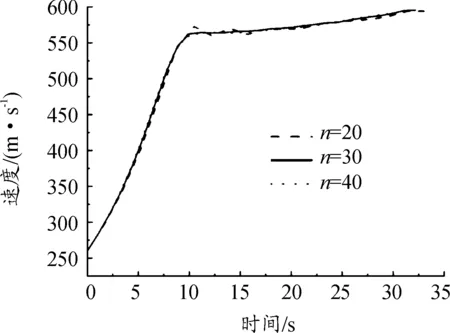
图3 n=20、n=30、n=40速度-时间仿真曲线

图4 n=20、n=30、n=40高度-射程仿真曲线

图2表明：通过粒子群算法可以较快的算出一条初始弹道，计算用时与n的大小有关。计算用时可以通过程序内的相应命令得到。当n分别取20、30和40时，平均用时为7.76 s、11.42 s和15.67 s。

图3和图4表明：初始弹道的可行性、精度和计算量也与n的大小有关。n的值太小会导致弹道不可行、精度较低，太大又会导致计算量增加。通过多次试验发现，当n≤20时，弹道的可行性和精度都很差。n≥30发现再增加n的值所计算出的结果差别不大，而且继续增加n的值，弹道的计算量会显著的增加。这表明在满足方案设计要求下，选取n=30为宜，可以做到初始弹道的可行性、精度和计算量三者兼顾。此外，由于粒子群算法的随机性，每次解得的初始弹道也不完全相同。

以攻角为控制变量，选取n=30，得到初始弹道，利用高斯伪谱法的取点规则取点，得到SQP算法的初值，代入求解得到最终优化设计弹道。通过反复计算发现，取点数N取10到20之间为宜。为了更好的在图上表现出高斯伪谱法的取点规则，这里选取N=12(加上τ0，τf，构成图中弹道的14个离散点)。同等条件下，随意选取SQP算法的初值(本文直接选用了一个初始化粒子)，仿真结果如图5、图6、图7所示。

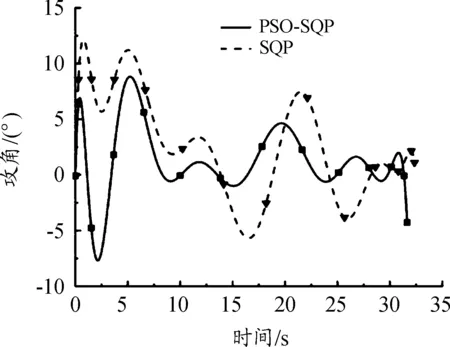
图5 攻角-时间仿真曲线

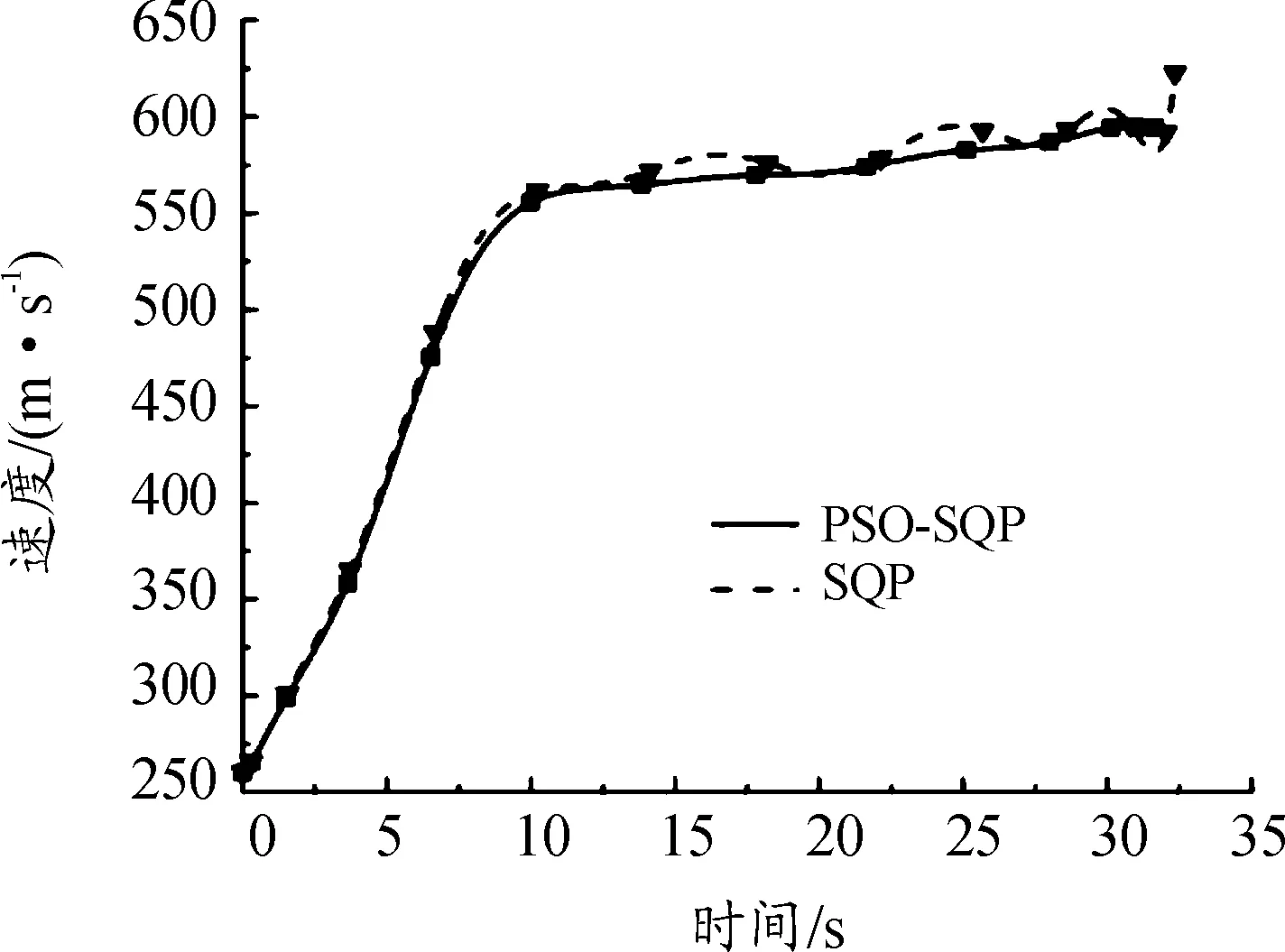
图6 速度-时间仿真曲线

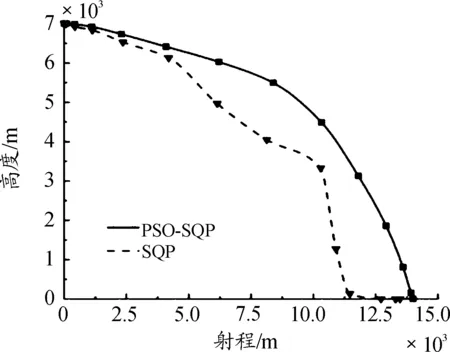
图7 高度-射程仿真曲线

图5、图6、图7表明：在满足约束条件的前提下，使用PSO-SQP算法完全优于仅使用SQP算法计算出的弹道。此外通过比较图3(n=30的速度曲线)和图6(PSO-SQP的速度曲线)，可以发现最终弹道相较于初始弹道，飞行时间从32.20 s缩短到了31.63 s。

仿真结果表明：仅用SQP算法求解弹道优化设计问题，由于选取问题，很难求得最优解，利用粒子群算法可以很好地解决SQP算法的初值依赖的问题，增加了得到最优解的可能性。并且计算出的最终设计弹道相较于初始弹道，也更好地符合了方案设计的预期效果。

5 结论

针对空地导弹快速打击地面目标的弹道优化设计问题，提出了一种基于PSO-SQP算法的优化方法，通过研究分析和仿真结果得出：利用高斯伪谱法离散约束条件，将最优控制问题转化为非线性规划问题，可以用较少的节点获得较高的精度。利用粒子群算法可快速、有效的选取初始弹道。本文提出的算法流程可以更快更有效地解决弹道优化设计问题，可为工程设计提供参考。