基于XGBoost的出水氨氮和总磷浓度的软测量研究∗

李 畅 潘 丰

（江南大学轻工过程先进控制教育部重点实验室 无锡 214122）

1 引言

随着社会经济的进步和发展，人类对水环境的污染日益加剧，污水的高效处理对于可持续发展有着越来越重要的意义［1］。氨氮是水体中的营养素，磷是藻类生长需要的一种关键元素，过量磷和氨氮是造成富营养化和赤潮的主要原因［2～4］。在2002年由国家环境保护总局发布的《城镇污水处理厂污染物排放标准》中规定一级A标准中NH4-N排放浓度最高为5mg/L，TP排放浓度最高为0.5mg/L［5～7］。

目前，针对水质中NH4-N浓度的测定，国家标准方法为纳氏试剂分光光度法，此外还有电化学分析法等［8］；针对水质中TP浓度的测定，国家标准方法为钼酸铵分光光度法，此外还有离子色谱法和罗丹明6G荧光分光光度法等［9］。这些测定方法操作繁琐，实时性不高，而相关的仪器仪表售价昂贵且维护成本较高。因此，研究如何能在低成本，操作简单的前提下实现出水NH4-N和TP浓度准确、实时的测量，具有重要的实际意义。

针对上述问题，基于数据驱动的智能化软测量方法在污水处理过程水质参数检测领域受到广泛关注和应用［10］。Deng［11］等提出基于径向基神经网络预测出水氨氮；乔俊飞［12］等使用递归RBF神经网络算法建立了出水NH4-N浓度的软测量模型；蒙西［13］等提出了一种基于类脑模块化神经网络的软测量方法实现对出水生化需氧量（BOD）和TP浓度的实时检测；Raduly［14］等通过前馈神经网络来预测多个过程变量。以上几种软测量方法虽可以基本达到实时预测的要求，但预测精度仍有待进一步提高。

2 软测量模型设计

针对污水出水NH4-N和TP浓度的软测量设计主要分为三部分：数据采集并使用KNN算法进行数据预处理；利用XGBoost算法进行软测量建模；使用网格搜索方法调整XGBoost的参数。

2.1 数据采集和预处理

污水处理采用目前使用最普遍的厌氧-好氧（A2O）工艺［15］，设备由一个生物反应器和一个二次沉淀池组成，其中生物反应器包含缺氧部和曝气部两部分。采集数据时，将传感器探头分别设置在进水初沉处、厌氧部末端、好氧部末端和出水处四个位置。数据采集系统如图1所示。

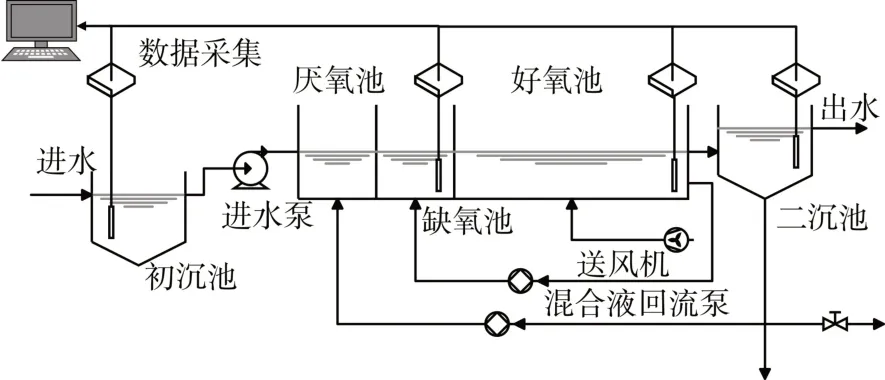
图1 污水处理数据采集系统

考虑到污水中各参数的采集难度以及对NH4-N和TP浓度的影响程度，选取温度（T）、碱度（PH）、溶解氧（DO）浓度和固体悬浮物（TSS）浓度四个参数作为辅助变量，将相应的传感器测量数据实时传送到数据采集仪，数据采集仪将实时数据发送到中央控制室的PC机中。

考虑到采集数据需要的人力和时间因素，确定采集8个批次的数据，每批次数据的周期为14天，采样间隔为15分钟，每批次数据共1344组。由于实际工业过程中，数据采集时可能出现数据缺失，因此文中采用KNN算法对采集的数据进行预处理，将缺失的数据填充完整。

KNN算法是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中k通常是不大于20的整数［16］。

KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别［17］。利用KNN算法对污水处理过程中采集的数据集进行填充包括以下步骤：

1）获取污水处理过程中采集的数据集，保留并供步骤7）使用；

2）将数据集中的数值型属性列进行数据标准化处理，以满足KNN模型支持的数据格式；

3）由于污水处理过程中每批次采集的无缺失值数据集的数据量不大，将2）中预处理后的数据随机拆分为训练数据集和验证数据集；

4）设定KNN模型参数k的区间为［4，6］，基于训练数据集和不同的KNN模型参数k，构建KNN模型簇；

5）利用模型优化目标函数筛选最优KNN模型，由于污水参数数据缺失值类型为数值型数据，目标函数S为

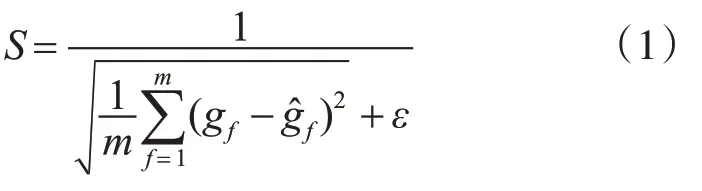
其中m表示验证集的数据样本数，gf表示验证集中每个样本在缺失值数据列的真实值，ĝf为gf对应的模型填充值，ε为平滑因子；

6）基于验证数据集的原始数据和预测数据，依据模型优化目标函数对KNN模型簇筛选得到最优KNN模型MQ；

7）基于缺失值数据构建缺失值矩阵，带入到模型MQ中得到预测数据集，并将其进行反标准化复原数据，完成缺失值的预测和智能填充。

为验证KNN算法的填充效果，随机选取某批次出水位置参数中TP列的100组数据，遍历此列数据并找出缺失值，使用KNN算法进行缺失值填充，填充效果如图2。

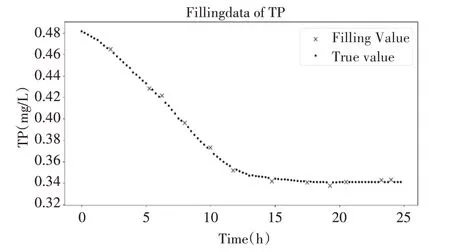
图2 使用KNN填充后TP列数据

2.2 软测量建模

采用XGBoost算法进行软测量建模，此算法是对梯度提升树（GBRT）算法的优化，相较于GBRT算法，XGBoost算法将目标函数进行了泰勒展开，并加入正则项［18］，可以有效降低模型过拟合的风险。

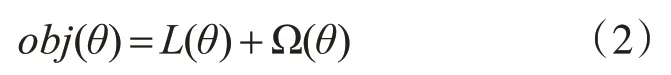
其中L(θ)为损失函数，Ω(θ)为正则化惩罚项，且回归树中的预测结果̂为

其中K为回归树的数量，fk(xi)为每一棵树的得分值，θ为使目标函数最小时所需要求出的参数。对式（2）进行整理可得：

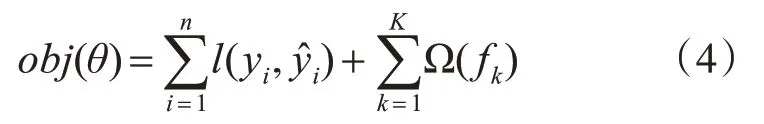
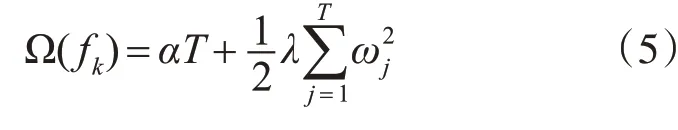
其中T表示第t棵树中总叶子节点的个数；ωj表示第j个叶子结点的得分值；α、λ为常数，表示正则惩罚中的参数［19］。

然后输入采集的6个批次的污水水质参数数据进行模型训练，对于第t轮迭代，模型的目标函数可表示为

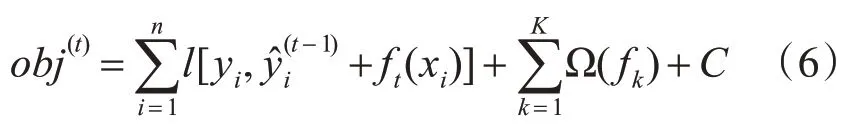
其中ft(xi)表示加入的第t棵分类回归树；常数C表示前t-1棵树的复杂程度。

进一步地，将第t轮迭代的目标函数用泰勒级数展开，可以得到：

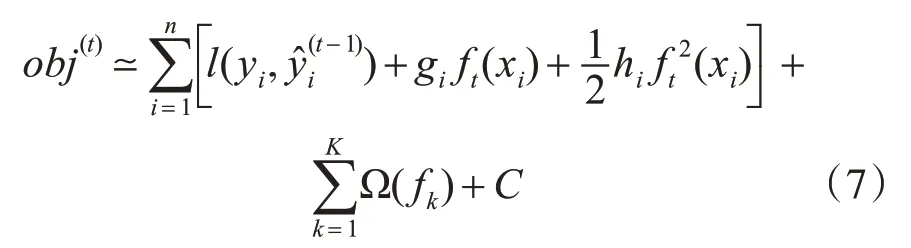
其中gi表示对的一阶导数；hi表示对的二阶导数。

进一步化简可以得到最终的目标函数：

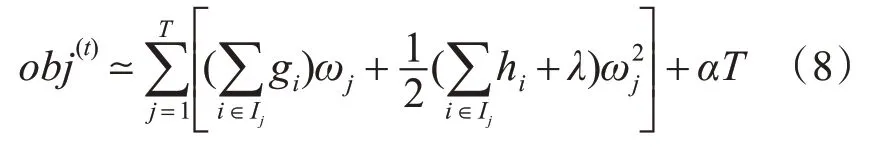
其中Ij表示在第j个叶子结点上的样本。

显然，此时只需寻找一个最优的权重值，即可获得最优的目标函数值。因此，将目标函数obj(t)对ωj求偏导并令其等于0，可以求出最优权重值为

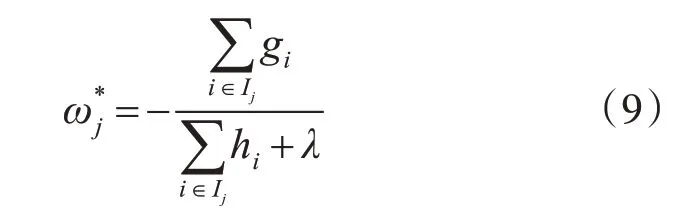
将式（9）带入式（8）可得最优的目标函数值为

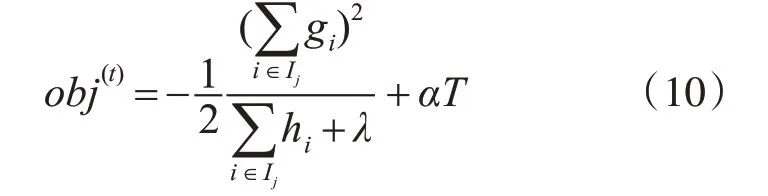
2.3 参数调整

XGBoost的参数调整一般指的是调整booster参数，booster参数取决于使用哪种booster，常用的booster有树模型和线性模型，由于树模型的性能一般比线性模型好得多，因此文中选择使用树模型并调整其相应的参数。

树模型主要参数及其特征如下［20］：

1）eta

学习速率，默认值为0.3，通过减少每一步的权重，可以提高模型的鲁棒性，典型值为0.01～0.4。

2）n_estimators

弱学习器的最大迭代次数，或者说最大的弱学习器的个数，默认值为100。

3）min_child_weight

决定最小叶子节点样本权重和，默认值为1。这个参数用于避免过拟合。当它的值较大时，可以避免模型学习到局部的特殊样本，但是如果这个值过高，会导致欠拟合。

4）max_depth

树的最大深度，默认值为6。值越大，模型会学到更具体更局部的样本。典型值为3～10。

5）gamma

指定了节点分裂所需的最小损失函数下降值，默认为0。这个参数的值越大，算法越保守。

6）subsample

控制对于每棵树随机采样的比例，默认为1。典型值为0.5～1。

7）colsample_bytree

控制每棵随机采样的列数的占比（每一列是一个特征），默认为1。典型值为0.5～1。

针对上述参数的调整，采用网格搜索方法，按照参数调整顺序，逐个寻找最优值。XGBoost参数调优的步骤如下。

1）确定eta为默认值0.1；

2）固定eta，确定n_estimators的搜索区间［50，800］，通过网格搜索找到其最优值；

3）max_depth和min_child_weight参数调优，搜索区间分别为［1，15］和［1，5］；

4）gamma参数调优，搜索区间为［0，1］；

5）subsample和colsample_bytree参数调优，搜索区间均为［0，1］；

6）保持eta和n_estimators的乘积不变，降低eta并使用更多的决策树。

文中通过上述过程的参数调整，得到分别针对出水NH4-N和TP浓度的两组booster参数如表1。

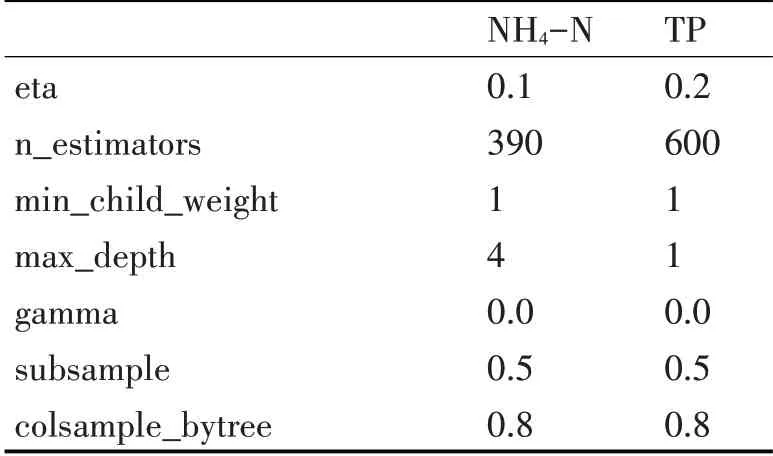
表1 调整后的参数值

3 仿真验证

3.1 调参前XGBoost算法仿真

将实际采集的6个批次水质参数数据输入并训练模型后，再使用两个批次数据进行验证，随机选取某批次出水NH4-N和TP浓度的预测效果如图3。

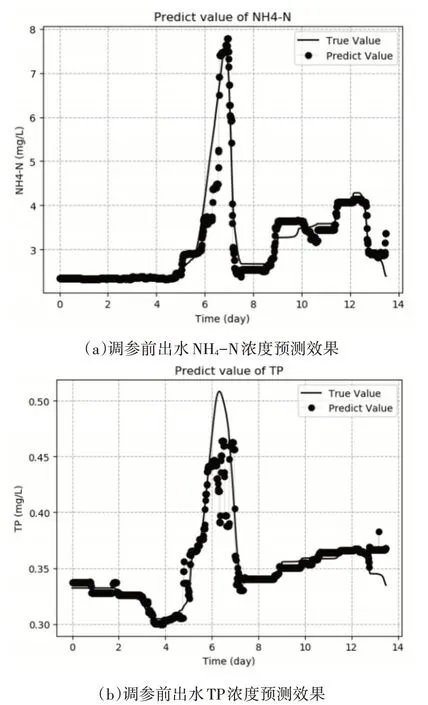
图3 调参前出水NH4-N和TP浓度预测效果

由预测图的拟合情况可以看出，在XGBoost算法中对于booster参数均使用其默认值的情况下，预测精度并不高，因此对参数的调整十分重要。

3.2 调参后XGBoost算法仿真

将booster参数按照2.3中的步骤调整后，该批次的预测结果如图4。

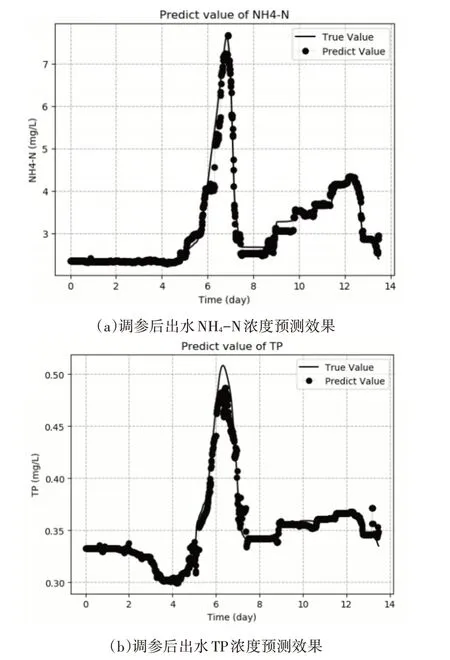
图4 调参后出水NH4-N和TP浓度预测结果

此时，从图中即可明显看出预测效果有了很大提升，为对比调参前后预测效果的变化，选择回归率（R-squared）、均方根误差（RMSE）和平均绝对误差（MAE）三个回归指标进行比较，将调参前后的回归指标保留4位小数记录如表2。

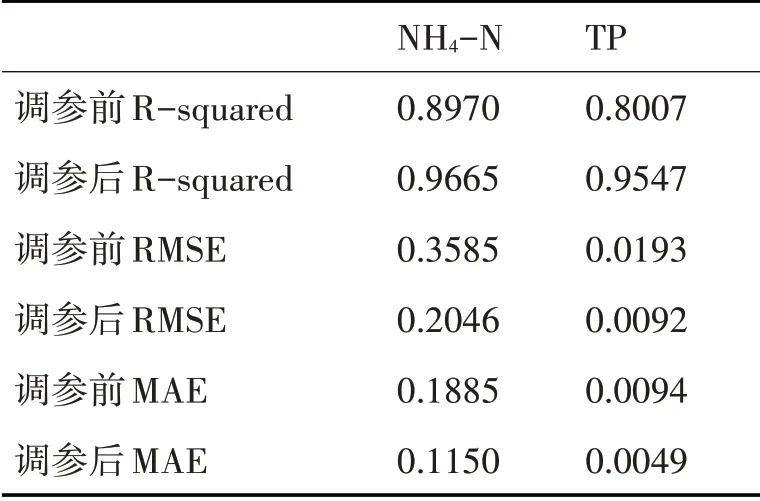
表2 调参前后XGB算法回归指标

对比调参前后回归指标，参数调整后回归率提升了7.75%，RMSE和MAE分别降低了42.93%和38.99%，显然调参后的预测效果大大提高。

3.3 算法对比

为检验XGBoost算法对于污水处理过程关键参数NH4-N和TP的预测精度情况，采用随机森林（RandomForest）算法、GBRT算法和套袋（Bagging）算法［23］分别进行建模并仿真，对NH4-N浓度的预测效果如图5、图6和图7所示。

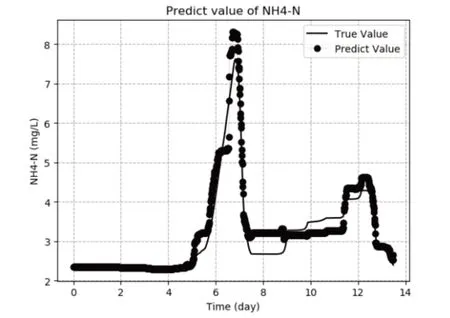
图5 RandomForest算法对出水NH4-N浓度预测效果

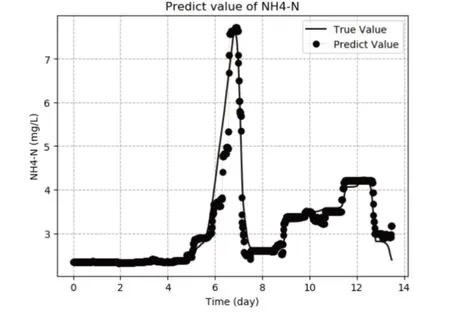
图6 GBRT算法对出水NH4-N浓度预测效果

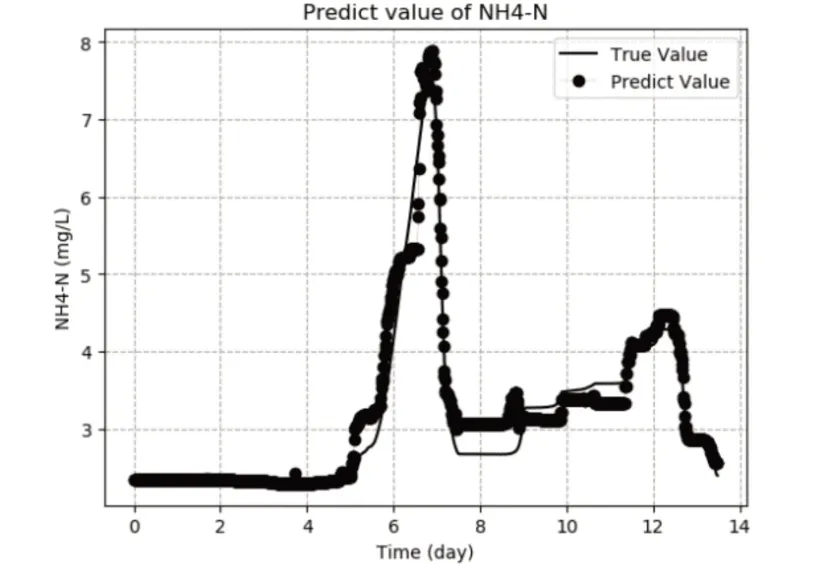
图7 Bagging算法对出水NH4-N浓度预测效果

为对比上述三种软测量方法与XGBoost算法对于出水NH4-N和TP浓度的预测效果差异，将四种软测量方法下的回归指标数据记录如表3。由表中数据可以看出，在污水处理关键参数的软测量问题上，使用RandomForest算法、GBRT算法和Bag⁃ging算法时，对于NH4-N和TP浓度的预测回归率均在95%以下，而XGBoost算法预测效果则明显优于RandomForest算法、GBRT算法和Bagging算法，且其回归率均可达95%以上。

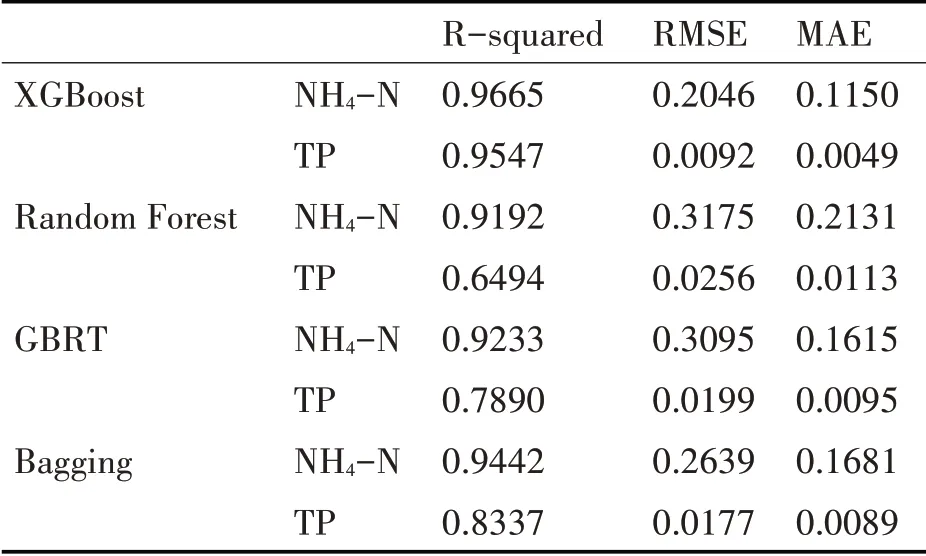
表3 四种软测量方法下的回归指标

4 结语

为解决污水处理过程中关键参数NH4-N和TP难以实时在线测量的问题，首先使用KNN算法进行缺失值填充，有效解决了实际采样数据存在缺失值的问题；进一步地，提出了一种基于XGBoost算法的软测量方法并建立软测量模型，实现了对出水NH4-N和TP的实时预测。仿真结果表明，该方法有较高的预测精度。