基于布谷鸟搜索算法的露天煤矿运输路径优化研究
张东旭
(1.中煤科工集团沈阳研究院有限公司,辽宁省抚顺市,113122;2.煤矿安全技术国家重点实验室,辽宁省抚顺市, 113122 )
0 引言
露天煤矿开采伴随着大量的土石方运输,运输投资占矿山总投资的40%~60%,所占投入成本较大,严重影响着矿山的经济效益。露天煤矿道路网络变化受时空演化规律所制约[1],随着工程位置的推进,不断有旧的道路被废除,同时又有新的道路被生成,如此周而复始,道路复杂多变,卡车运输路径很不固定。近年来,我国进入智能化露天煤矿发展阶段,无人驾驶技术逐渐成熟,合理的运输路径规划是实现矿山内无人驾驶卡车运行的基础和前提,也是降低矿山投入成本、提高经济效益的有效方式。
露天煤矿路径优化问题一直是矿山研究领域的热点问题,国内外专家学者已对其进行过大量的研究,并取得丰富的研究成果。孙臣良等[2]研究人员基于粒子群算法作为优化算法,以路面质量、坡度和承载能力等因素建立运输道路模型搜索最优路径。但算法中由于所有的粒子都易向局部最优解的方向飞去,粒子方向失去多样性,导致算法精度不高,且后期收敛速度越来越慢;Choi和Nieto[3]以改进的LCPA(least-cost path analysis)方法,在考虑地形起伏和沿途曲线的基础上,以最小化卡车的运输时间以及产生的燃料消耗为目标求解最优路径,但忽略了路网模型节点之间的拓扑关系;柴森霖等[4]研究人员基于改进遗传算法为方法,建立以最小时变运输功为目标的路径优化模型;刘光伟等[5]研究人员建立了基于选线道路费用最优的数学模型,将生物激励神经网络引入到路径基因编码过程中对遗传算法进行改进,以此提高算法的迭代收敛速度,但改进后遗传算法仍存在染色体的交叉和编译后,种群已无法产生优于本体的子代个体,出现局部最优的情况。
在以上研究中,由于优化算法在实现过程中的随机性,使得大多都存在优化算法易陷入局部最优解、收敛速度慢、建立路径优化模型时考虑影响因素不全面等问题。为了优化路径择优模型,提高算法收敛速度和精确度,本文通过对卡车工作过程中行驶路面状况进行分析,综合考虑卡车行驶速度、道路坡度、路面质量等因素,建立以最小运输功为目标的路径优化模型,以布谷鸟搜索算法为优化方法对最优路径进行搜索。该算法拥有独特的幂律规律莱维飞行行为,加快算法的局部搜索能力,并且能随机产生新解对上一迭代中的解进行更新,快速跳出局部最优解。最后以宝日希勒露天煤矿为实例应用进行分析验证模型的精确性与算法的有效性。
1 问题描述与模型建立
1.1 问题描述
露天煤矿运输路径优化即在道路网络中保证安全、经济效益与满足现场实际的条件下进行卡车行驶最优路径选取的问题研究[6]。传统的路径优化模型多是以最少运输费用或最短运输距离为目标而建立优化模型,其考虑的影响因素较为单一,但影响露天煤矿路径优化的因素众多,包括维修成本、油耗成本、路面质量等。本文根据露天煤矿的现场地理环境,找出卡车从装载点到卸载点往返之间的最小运输功,以此求出最佳运输路径。露天煤矿运输路径示意图如图1所示。
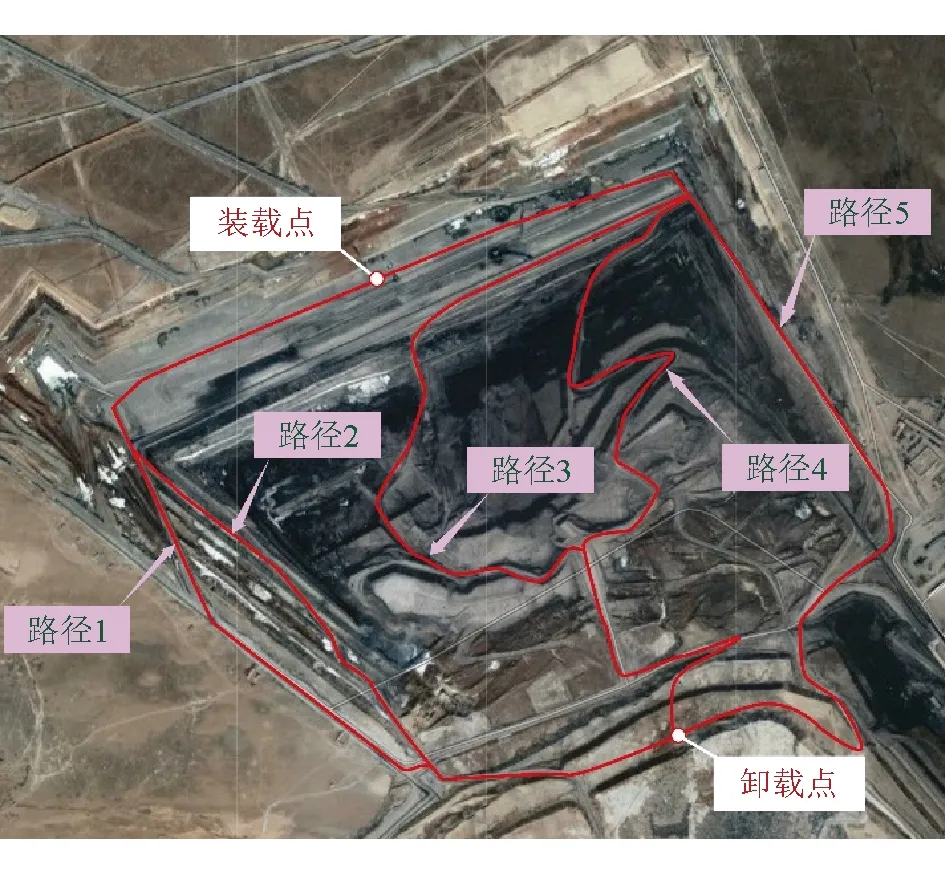
图1 露天煤矿运输路径示意图
1.2 模型建立
露天煤矿运输路径优化问题可描述为:在露天煤矿运输系统网络中,采剥工作面节点(装载点)与排弃工作面节点(卸载点)之间存在多条可供选择的运输路径,但每条运输路径卡车行驶消耗运输功差别很大,利用优化算法动态搜索出一条运输路径,使此路径卡车行驶消耗运输功最小。假设露天煤矿道路网络表示为G{V,E,W},其中V={1,2,3,…,n}表示路网中所有非空节点集合;E表示弧段集合,i,j节点之间弧段ei,j=(i,j)∈E;W表示卡车经过各弧段消耗的运输功所组成的矩阵。
1.2.1影响因素分析
影响卡车做功的因素众多,但路面质量以及路段坡度对卡车行驶消耗的程度不可忽视。路面质量的好坏直接影响着卡车克服滚动阻力所做功的大小,路段坡度越大卡车克服坡度阻力做功越大。以卡车重载经过之后路面留下车辙程度为评判依据,将路面质量划分为5个等级及其不同等级所对应的滚动阻力系数见表1。

表1 路面质量等级及滚动阻力系数
1.2.2最优路径规划模型
假设卡车在相同等级的路面上行驶的速度是一致的,卡车速度在装载点与卸载点之间服从正态分布。一条完整路径总运输功是由组成该路径的各路段运输功的加和,而卡车在行驶过程中总运输功主要由克服重力做功和克服阻力做功这2部分组成。
卡车在行驶时克服重力做功见式(1):
We=G·H
(1)
式中:We——克服重力做功,N;
G——卡车载重,t;
H——坡路高程,m。
卡车在行驶时克服阻力做功见式(2):
(2)
式中:Wf——克服阻力做功,N;
Ff——滚动阻力,N;
Fw——空气阻力,N;
Fp——坡度阻力,N;
L——卡车的实际运输距离,km;
f——滚动阻力系数;
C——空气阻力系数;
A——卡车迎风面积,m2;

μ——坡度阻力新系数,μ=sinθ。
卡车以最小运输功为目标的最优路径规划模型见式(3):
(3)
式中:n——节点个数,个;
i——第i个节点;
j——第j个节点;
Fij——道路阻力,N;
Sij——道路状态变量,其中Sij=0时,eij为不可行弧段,Sij=1时,eij为可行弧段;
Lij——弧段eij的实际长度,km;
eij——ij节点之间弧段;
R——可选弧段集;
△Hij——路段eij的高程差,km。
露天煤矿工作空间具有固定封闭的特性,岩石剥离物的排弃空间相对固定,不能随机选择卸载点,在道路网络卡车运输工作中需给定起始节点与目标节点。而重力做功只跟卡车从初始节点到终了节点的高程差有关,与运输路径无关,由于卡车选择最优路径之前已确定好装载点与卸载点的位置,因此,所选路径集中,重力做功相同,在建立最小运输功模型时可略去重力做功以简化模型,仅比较克服阻力做功即能选出最优路径。
当装载点与卸载点之间卡车重载或空载行驶时克服阻力做功最小即为最优路径。最优路径规划模型可简化为式(4):
(4)
2 布谷鸟搜索算法
剑桥大学YANG X S和Suash Deb教授通过观察某些种属布谷鸟的寄生性育雏行为,并发现将其行为转化为数学方式可有效求解最优化问题,于是2009年提出了布谷鸟搜索算法CS(Cuckoo Search)[7]。研究发现,CS算法比遗传算法(Genetic Algorithm,GA算法)、人工蜂群算法(Artificial Bee Colony,ABC算法)和粒子群算法(Particle Swarm Optimization,PSO算法)等典型群体智能算法具有更高的效率,可在部分求最优化函数下得到相对较好的优化结果[7-9]。目前,CS算法已被应用于多种工程优化问题[10]。
CS算法的主要思想是种属布谷鸟类的巢穴寄生行为以及其独有的幂律规律莱维飞行行为。在应用CS算法求解工程实例问题时,需假设以下几项理想化规则:
(1)假设每只布谷鸟每次随机选择寄生巢穴并只下1个蛋;
(2)具有优质蛋的最佳巢穴将保留至下一代;
(3)寄生鸟巢数量n不变,可认为鸟巢、蛋、函数解三者数量相等,蛋被寄主发现后丢出鸟巢或弃巢新建的概率为Pa∈[0,1]。
基于以上3条准则,从实际角度出发,设置概率Pa控制选择局部随机游走或全局随机游走,巢穴中的寄生蛋即为函数的一个解,算法迭代过程中的目标是利用优质解替换掉劣质解。当采用局部随机游走更新方式表示见式(5):
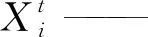
∂——步长缩放因子;
S——步长;
⊗——元素点乘;
H(u)——一个 Heaviside 函数;
Pa——概率;
ε——从均匀分布中抽取的随机数;
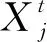
采用全局随机游走更新方式表示见式(6):

(6)
式中:β——莱维指数;
Lévy(β)——服从莱维指数β的莱维飞行搜索路径。
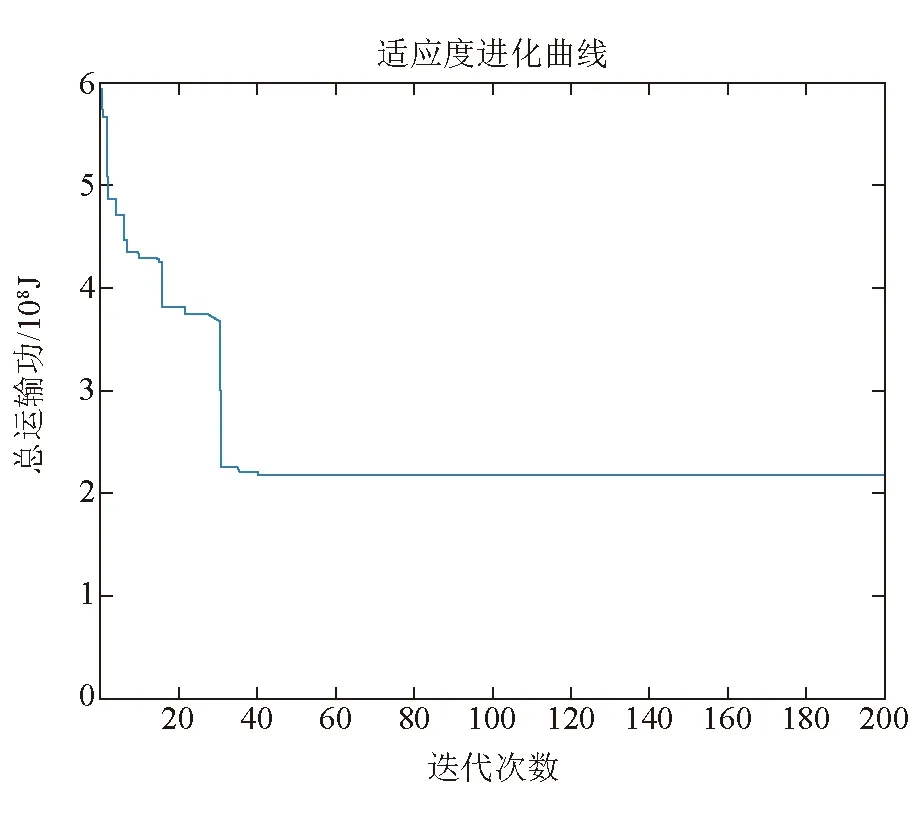
通过式(5)或者式(6)进行位置更新后,生成随机的数字r(r∈[0,1]),对r与Pa进行比较,如果r 以下为CS算法伪代码: 1.建立优化目标函数; 3.while(t 4.随机取一个布谷鸟; 5.通过Lévy飞行产生一个解; 6.评估解的质量或目标函数值fi; 7.从n个鸟巢中随机抽取一个(假设为j); 8.iffi 9.将j用解i代替; 10.end if; 11.一部分(Pa)糟糕的巢被抛弃; 12.新巢(解)由式(4)产生; 13.保存最佳的解; 14.排列解找出当前最佳; 15.更新t←t+1; 16.end while; 17.后处理与可视化。 经上述描述可以看出,CS算法具有设置参数较少、步骤简单、容易实现等优点,有着较好的全局搜索能力。众多学者研究并在实例中应用后表明布谷鸟搜索算法是非常有效的[11-12]。在应用布谷鸟算法求解露天煤矿最优化问题时,由于路网模型存在拓扑关系,各节点之间不能采用随机的方式进行联通,因此,在种群初始化时,从起始节点开始,选择相邻节点作为第二位置,并重复此步骤直至目标节点为止,由此构成一条完整路径。 为了验证CS算法在露天煤矿运输路径优化中的有效性,在Windows 10操作系统平台的MATLAB R2018a进行数值仿真实验。选取宝日希勒露天煤矿2019年12月路网数据进行分析,整理出该露天煤矿路网装载点至卸载点间共有27个节点、31条路段。宝日希勒露天煤矿路网分布示意图如图2所示。 图2 宝日希勒露天煤矿路网分布示意图 该矿应用220 t的MT4400型矿用运输卡车,迎风面积A=51.28 m2。运行布谷鸟搜索算法时,发现设置参数初始鸟巢数量n=25,概率Pa=0.25,步长缩放因子∂=0.5,莱维指数β=0.8,迭代次数设为200次时,算法收敛最快。算法运行得出的卡车行驶最优路径与所对应消耗的克服阻力做功见表2,该矿卡车实际运输路径与所对应消耗的克服阻力做功见表3。 由表2和表3可以看出,编号1和4的实际运输路径即为最优路径;编号2和6的最优路径虽然运输距离大,但克服阻力做功要小于现场实际的运输路径;编号2、3、7、8的现场实际运输路径不是最优运输路径。因此可知,以运输路径最小为优化目标不能确定出最优路径。 由上述分析可知,当给定起始节点与目标节点,算法能在保证精度的前提下快速收敛于全局最优解,例如本实验给定起始节点2与目标节点21,最终得出路径2-3-4-27-8-21为最优路径。CS算法迭代过程如图3所示。 表2 装载点到卸载点最优路径及所对应消耗的克服阻力做功 表3 装载点到卸载点现场实际运输路径及所对应消耗的克服阻力做功 图3 CS算法迭代过程 本文将卡车行驶过程中克服重力做功与克服阻力做功之和作为卡车消耗总运输功,以最小化总运输功为目标建立了露天煤矿卡车运输路径优化模型。在给定起始节点与目标节点后,以布谷鸟搜索算法搜寻卡车行驶最优路径,结合宝日希勒露天煤矿现场实际情况,结果表明运输路径最小为优化目标不能确定出最优路径,而在综合考虑卡车行驶速度、道路坡度、路面质量的因素前提下,建立以最小运输功为目标的路径优化模型,以布谷鸟搜索算法为优化方法对最优路径进行搜索,该算法收敛速度快,在一定程度上达到了理想优化效果,具有较高的实用价值。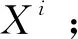
3 实验与分析



4 结语

