基于真实头模型的经颅磁声电刺激感应电流密度仿真分析
刘亚泽,张 帅,郭 梁,陈昕彤,武健康
(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室,天津 300130; 2.河北工业大学 河北省电磁场与电器可靠性重点实验室,天津 300130)
近年来脑功能疾病如抑郁症、痫病和帕金森病的发病率逐年上升。据世界卫生组织统计,我国患有神经类疾病的人群数量位居世界第一,给社会和国家带来了沉重的负担[1]。此外,随着社会经济的高速发展,巨大的生活和工作压力增加了诸如抑郁症和自闭症等精神类疾病的发病率。因此,深入开展脑功能探索和发展相应的治疗技术犹为迫切[2]。
在诸多治疗手段中,无创脑调控技术以安全、无痛、操作可重复等优点获得了越来越多的关注和认可。常见的几种无创脑调控技术有:经颅直流电刺激(transcranial Direct Current Stimulation,tDCS)、经颅磁刺激(Transcranial Magnetic Stimulation,TMS)、经颅超声刺激(Transcranial Ultrasound Stimulation,TUS)以及经颅磁声电刺激(Transcranial Magnetic-Acoustical Electrical Stimulation,TMAES)。其中,TMS和tDCS已被应用于神经性疾病的治疗,但由于二者存在空间分辨率低(cm级)、激深度不足等缺点,其在临床上的应用受到了限制[3-5]。TUS是一种使用低强度的超声波作用于靶组织来调控神经元放电的技术。超声波具有良好的穿透性和较高的分辨率[6-7]。TUS被证实可以用于皮质组织,且有用于深度刺激大脑神经的潜力。但是由于超声有引发热效应导致靶点组织损伤的可能,因此需要在安全性层面进行探索[8]。
TMAES是在上述神经调控手段的基础上发展出的一种新型神经调控技术。该技术使用低强度的超声和静磁场共同作用于神经元,通过磁声耦合效应产生感应电流从而调节神经元的放电活动[9]。TMAES不仅有与TUS相当的高空间分辨率和穿透深度,且其形成有效刺激的空间峰值时间平均声强阈值较TUS而言更低(降低约80%)[10],因此TMAES具有更好的安全性。
2003年,文献[11]提出了无损伤的超声组合磁场的神经刺激设想。2006年,研究人员在静磁场中放置了导电凝胶,向其施加超声信号,检测到了感应电流,并将其与超声回波进行频谱分析,得出了两者中心频率一致的结论[12]。2015年,文献[13]对导电样本进行了磁声耦合的初探,证实了磁声电刺激的可行性。2016~2017年,文献[14]研究了基于Hodgkin-Huxley神经元模型的经颅磁声刺激的放电活动;文献[15]探究了经颅磁声刺激作用下的神经元放电频率适应性。2018年,本课题组研究了基于Izhikevich神经元模型的TMAES对快放电和常规放电神经元的影响[16]。
但是,以上研究均未考虑人体头颅的几何结构和声学非均匀性对TMAES的影响。使用真实头模型研究TMAES对于获得精确的颅内声场分布和感应电流密度分布有着重要意义,有助于深入了解影响刺激效果的因素。因此本文首先构建了三维真实头模型,然后对其进行TMAES的仿真分析,获取在平面超声换能器的作用下采用不同刺激参数所得到不同的感应电流密度分布,旨在探寻TMAES刺激效果和超声频率之间的关系。
1 实验方法
1.1 TMAES原理
生物组织中含有带电离子,将其置于静磁场中,沿着垂直磁场的方向施加超声波,生物组织内的带电离子就会产生振动。在洛伦兹力的作用下会发生正负离子分离,从而产生感应电流,达到电刺激的目的。磁声电刺激的原理如图1所示。
带电离子受到洛伦兹力为
F=qv×B0
(1)
式中,F为洛伦兹力;q为带电粒子的带电量;v是粒子振动速度;B0是静磁场的磁感应强度。生物组织产生的感应电流密度为J,计算式如式(2)所示。
(2)
将式(1)带入式(2)中得
J=σv×B0
(3)
其中,σ为生物组织的电导率;P为该粒子所处位置的声压。超声在该介质内的传播速度与c0存在如下关系
(4)
因此,生物组织在TMAES的作用下产生的感应电流密度如式(5)所示。
(5)
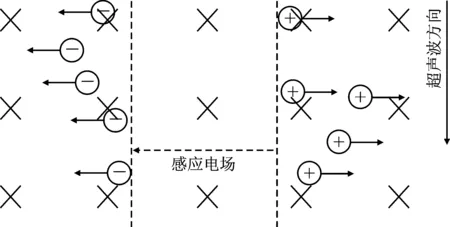
图1 磁声电刺激原理Figure 1. Principle of TMAES
1.2 超声传播特征
超声波传播路径当中任意一点的声压都可以使用Helmholtz-Kirchhoff积分定理计算,计算式如下
(6)
其中,ω为角频率;ρ0为超声传播介质的密度;V是超声换能器的振幅;k为所求点超声波周期数;R=|r-r′|;ρ为向量的模,积分区域是声源的范围。令Vρ0c=1,可简化超声传播路径轴线上的声压大小的计算。取声压P(r)的绝对值作为因变量,超声在传播轴线上的声压分布如图2所示。
在公路工程施工过程中,很多高速公路路面工程的建设单位,没有能够按照设计规定的要求做好原地表土淤泥等弃土的运输保存。而是在开发之后将弃土放在排水沟的两侧,导致积水未能及时排出。因此在排水沟设计过程中,可以将开挖后的淤泥应用于绿化工程中,以减少工程后期土方运输困难问题。同时,在排水沟设计深度上,需要按照当地的降雨条件以及路基高度进行确定[2]。
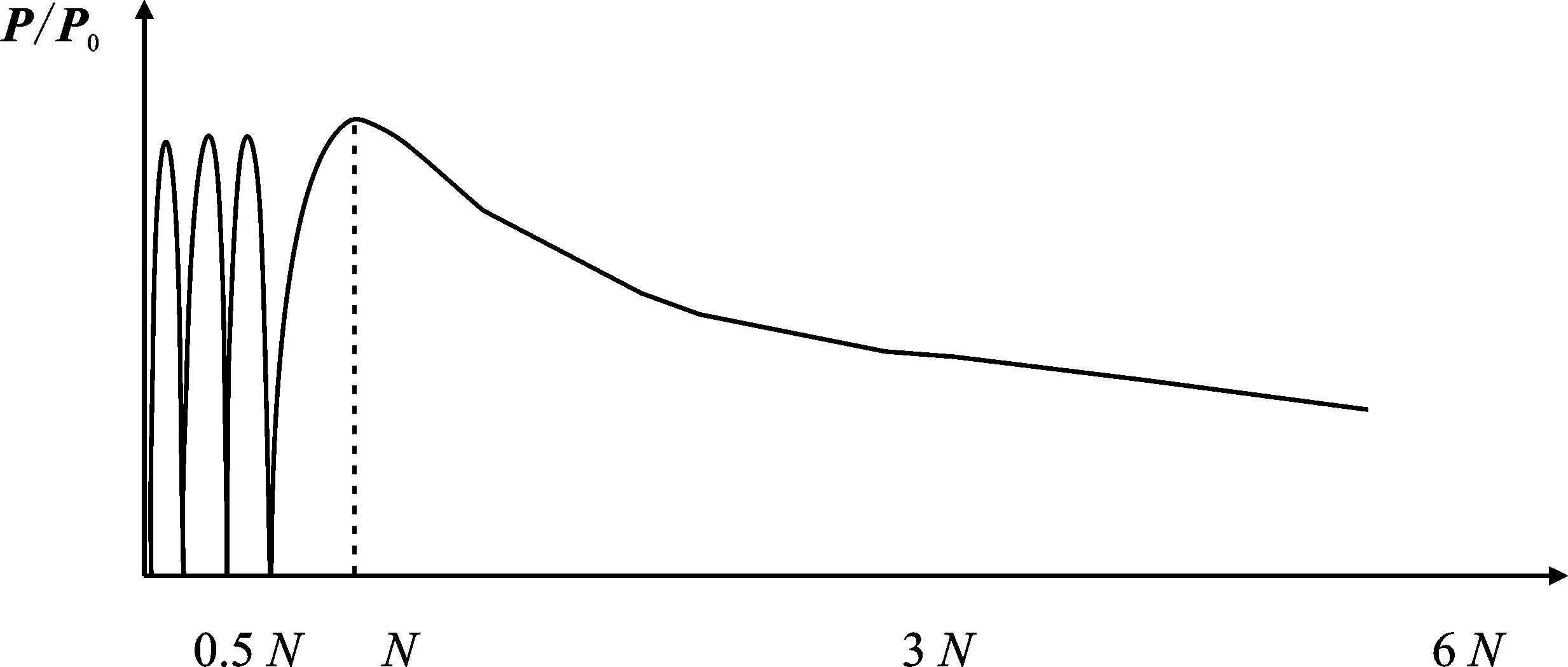
图2 声压轴向分布Figure 2. Distribution of acoustic pressure along axis
通过观察声压分布图可以看出,超声在0
根据频率为250~500 kHz时超声波穿透老鼠颅骨的衰减较小的结论[17],本文采用直径为30 mm的平面超声换能器,选取300 kHz、400 kHz、500 kHz的超声波研究超声频率对TMAES聚焦性的影响。为了避免TMAES作用的靶点进入超声近场区,以超声在水中传播为参考,根据超声近场计算式,求得3种频率的近场长度分别为45 mm、60 mm和75 mm。因此将超声换能器置于头模型正上方75 mm处,振动面垂直向下发射超声波。
1.3 真实头模型的构建
本文使用Materialise公司的Mimics17.0进行建模。首先将人体头部CT数据导入到Mimics中,对CT数据进行阈值分割。阈值分割是一种根据不同组织在CT图像灰度值上的差异,将其提取成为二值化数据的操作。颅骨的阈值分割见图3。
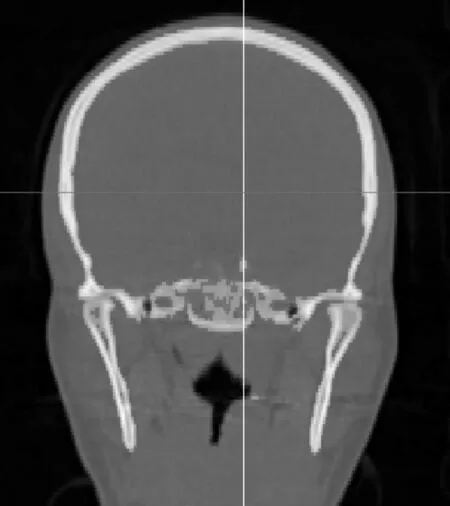
图3 颅骨阈值分割冠状面视图Figure 3. Skull thresholding segmentation coronal view
使用同样的方法提取出头皮和大脑组织。然后对获取的二值化数据进行三维计算生成三维面片模型。初始的三维面片模型表面不平滑,内部存在细微孔洞,不利于有限元计算。为提高模型质量,本文对初始模型进行平滑、填补等优化操作后获得高质量、易剖分的三维面片模型。但面片模型无法用于有限元计算,需要将其三维实体化并且进行有限元剖分,完成这些操作后最终获得真实头模型如图4所示,模型共包含893 511个单元。其声学、电磁学参数见表1。

图4 真实头模型Figure 4. Realistic human head model
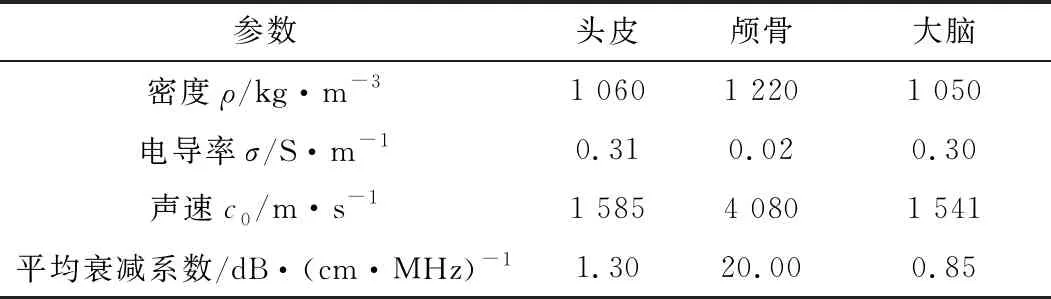
表1 真实头模型参数
2 仿真结果
2.1 TMAES感应电流密度分布
使用有限元仿真软件计算出真实头模型在1 T的磁场,500 kHz超声作用下的TMAES感应电流密度分布,如图5所示。
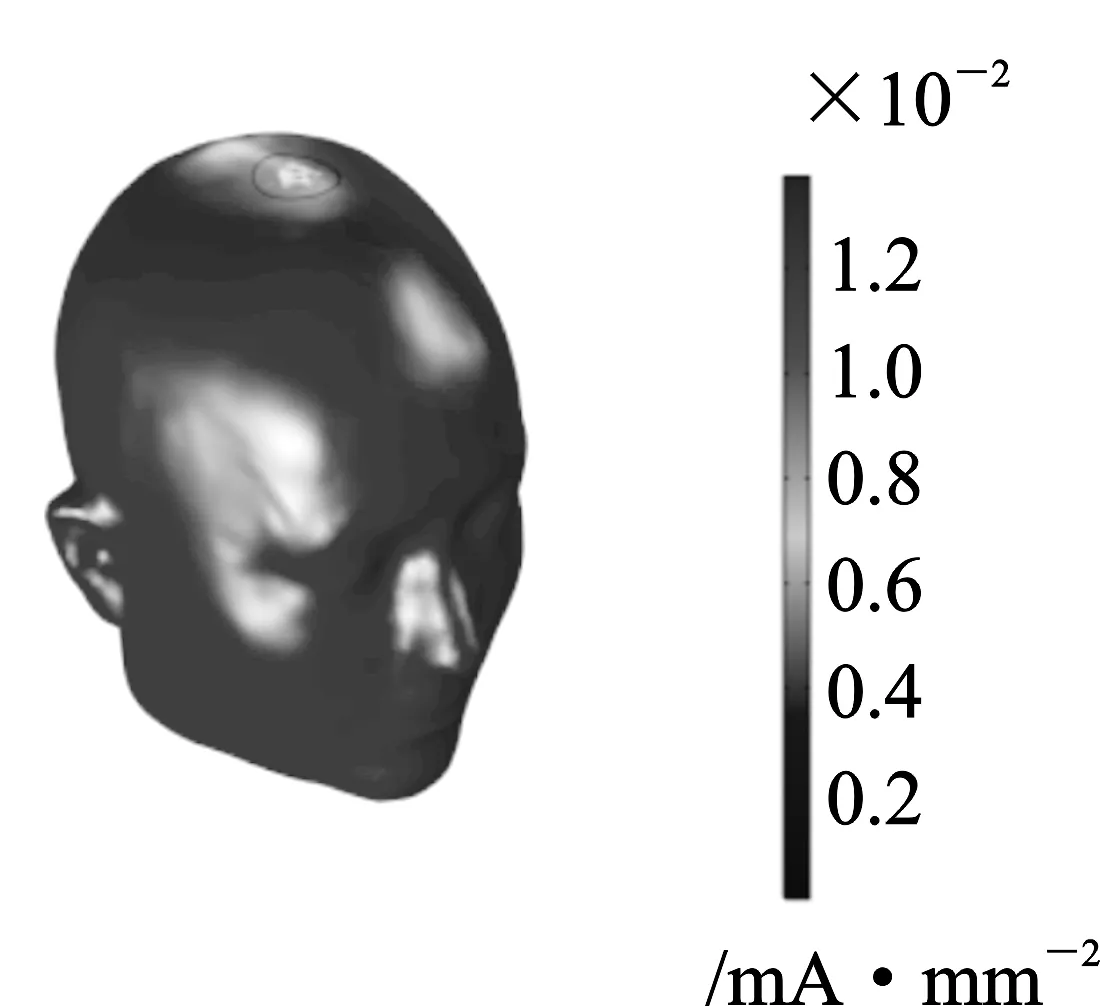
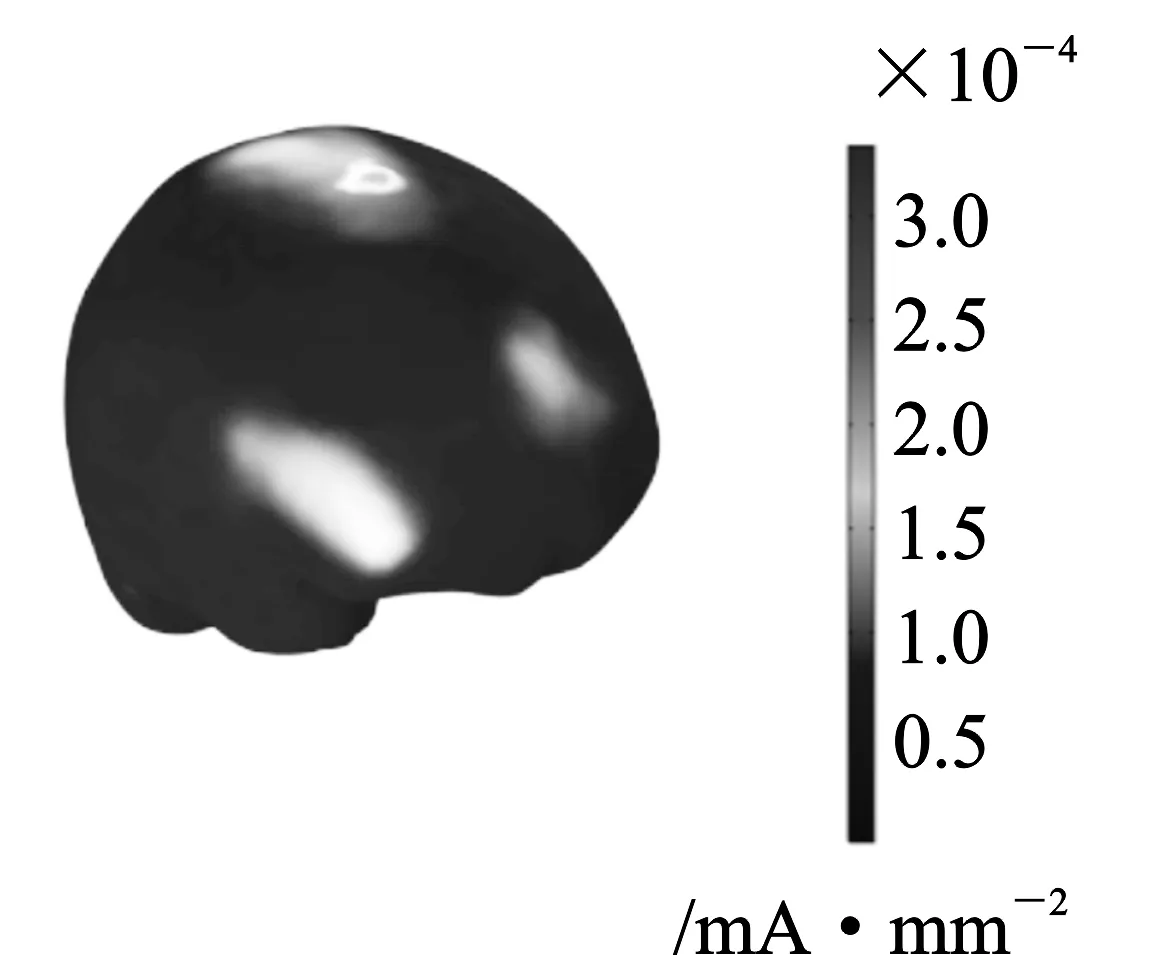
(c)图5 感应电流密度表面分布(a)头皮 (b)颅骨 (c)大脑Figure 5. Distribution of induced current density on the surface (a) Scalp (b) Skull (c) Brain
超声波从头部冠状面和矢状面交线顶端入射头皮,穿过颅骨达到大脑内部,在静磁场的作用下产生感应电流。感应电流在3种组织的表面形成了近似圆形的焦斑。这一现象初步表明TMAES的聚焦性能和穿透性能良好。
取大脑矢状面和水平截面的数据绘制了感应电流密度分布图,如图6所示。

(a)

(b)图6 感应电流密度内部分布(a)矢状面 (b)水平面Figure 6. Distribution of induced current density inside the model (a) Sagittal plane (b) Horizontal plane
为了进一步定量地去评估感应电流密度的深度特性和聚焦特性,本文规定了3个评价指标:(1)刺激强度Jp。刺激强度是反应刺激强弱的指标,刺激强度越大,对神经元的调节作用就越强,取大脑内感应电流密度的峰值作为判断刺激强度的依据;(2)刺激长度l。刺激长度是判断TMAES深度特性的重要依据,某些脑功能疾病的发病脑区位于大脑深处,需要使用刺激长度来判断是否刺激到目标靶区。本文根据感应电流的轴向分布特点,规定l为感应电流密度在超声换能器中轴线上(Z轴)由不小于1/2Jp的点组成的区域的长度;(3)聚焦面积S。聚焦面积反映了TMAES的空间分辨率。在对特定脑区的神经元进行调控时应当尽量减小对非靶区神经元的刺激,因此设立了聚焦面积这一指标来衡量感应电流密度的聚焦性能。本文根据感应电流密度在超声换能器的径向分布特征,规定截取S的水平面是刺激长度l区间的中点所在的水平面。S是由该平面内不小于1/2Jp的点组成的区域。
经过测量,超声频率为500 kHz时TMAES的Jp为0.23 mA·mm-2,l为23.2 mm,S为26.4 mm2。刺激深度约2~3 cm,可以刺激到皮质深层的脑区;聚焦面积是mm级别,优于TMS(cm级别)。由此可见,TMAES在无创脑调制技术中有着良好的应用前景。
2.2 频率对刺激效果的影响
超声波的频率对感应电流密度的分布有着决定性的影响,并且影响机制复杂。首先,频率的不同会改变超声波在颅骨内的穿透性;其次,超声波的频率和功率也存在关系,频率越高,超声功率越大;最后,频率的变化也会导致超声穿过不同介质产生的反射和折射存在差异。本文为了探究超声频率对感应电流分布的影响,分别使用频率为300 kHz、400 kHz和500 kHz的超声波对真实头模型施加了TMAES,并获得了感应电流密度分布数据。取超声换能器轴线上的数据绘制感应电流密度轴向分布,如图7所示。
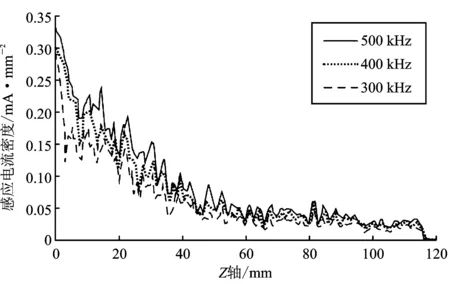
图7 感应电流密度轴向分布Figure 7. Axial distribution of induced current density
根据文中确立的评价指标,得出在3种超声频率下的Jp分别为0.29 mA·mm-2、0.30 mA·mm-2以及0.32 mA·mm-2;l分别为22.5 mm、23.0 mm以及23.2 mm。取得刺激长度之后,选取各自刺激长度区间的中点所在水平面的数据,绘制感应电流密度径向分布,如图8所示。根据S的计算标准,得到3种频率下S分别为14.5 mm2、19.6 mm2和26.4 mm2。评价结果总结如表2所示。
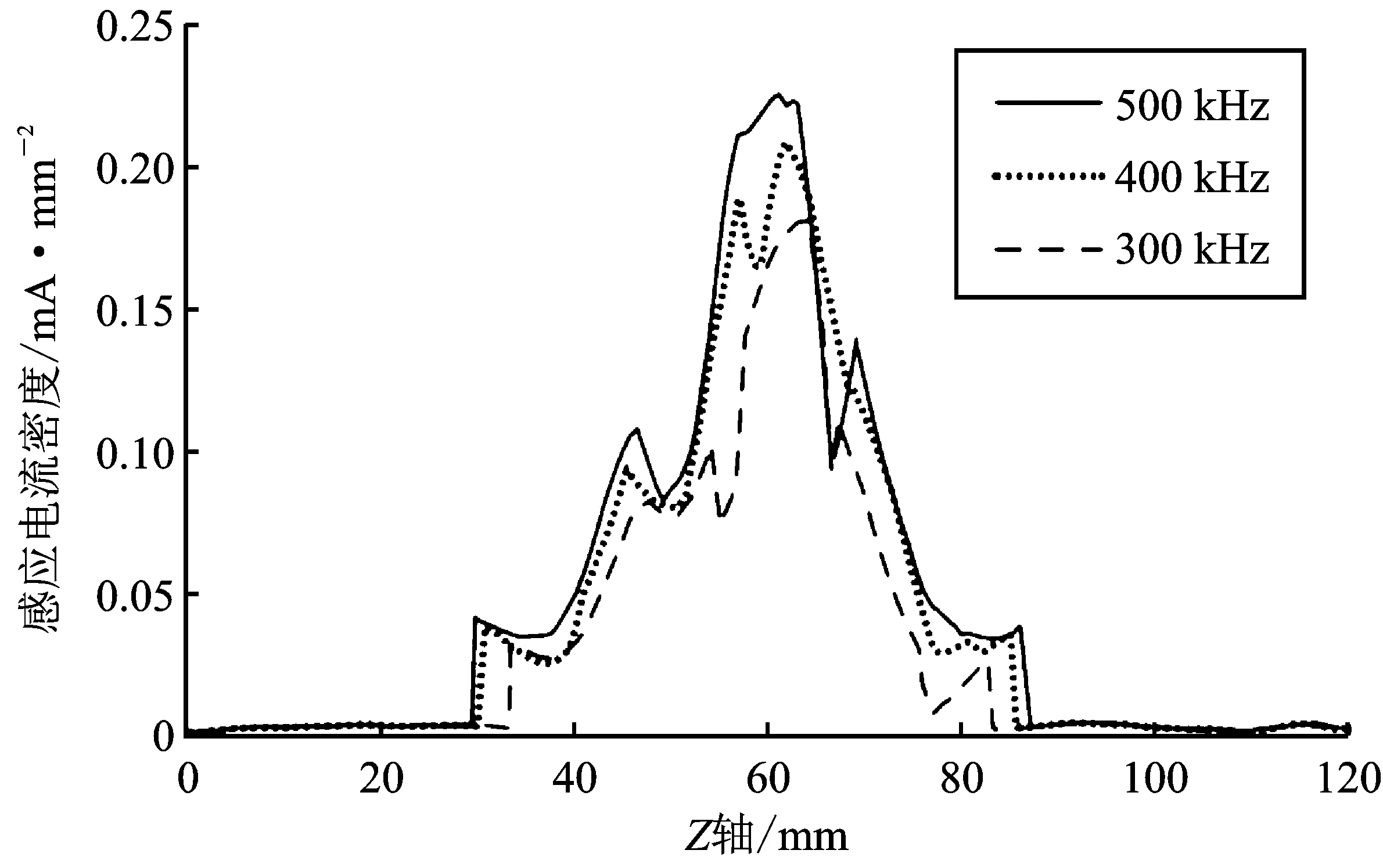
图8 感应电流密度径向分布Figure 8. Radial distribution of induced current density

表2 TMAES评价结果
由表2可知,刺激强度、刺激长度以及聚焦面积都随着刺激频率的增加而增加。本文选取了超声透射效果较好的低频率段进行仿真分析,不能代表全部频段都符合该规律。下一步可以扩大超声频率范围,以便寻找TMAES的最佳刺激频率。
3 结束语
TMAES是一种刺激深度良好、空间分辨率高的神经调控技术。感应电流密度的分布和超声波的频率存在制约关系。本文研究了低频段(300~500 kHz)的超声频率对感应电流密度聚焦性的影响。结果表明,在低频段超声中,TMAES刺激强度、刺激长度以及聚焦面积与超声的频率呈正相关。本文使用的真实头模型是由基于特定个体的头部CT图像数据构建而成,与其他个体存在差异。使用真实头模型进行有限元仿真分析令结果更加贴近实际情况,为未来进一步提高TMAES聚焦性的研究提供了理论指导。
本文也发现了TMAES可能存在的问题,例如头皮处的感应电流强度较大,可能会引起患者头皮的不适。若想解决这一潜在问题,一方面可以尝试改变磁场在头部的分布;另一方面可以考虑改进超声聚焦模式。

